1 INTRODUCTION

A transformation of a structure, in particular, a microstructure to a nanostructural state can lead to marked changes in the physical properties of 2D materials for nanoelectronics. An increase in the ratio of the surface area to the volume and the particle transfer to the region with quantum effects are important factors of changing the physical characteristics of 2D materials [1–3], in particular, graphene [4]. Among such characteristics are the electron conductivity, the thermal stability, the structural flexibility, and the high specific surface area.

The structural features of a monolayer graphene enable to charge carriers to move freely in planes, which is important for miniaturizing modern devices. Some studies indicate the possibility of varying the energy gap and the charge carrier concentration in graphene and to observe the quantum Hall effect at room temperature [5, 6]. The graphene properties are changed using both chemical and physical techniques of modification of the structure, in particular, the implantation of doping impurities [7–12]. Such doping impurities as 2p elements are comparatively easily implanted into a graphene sheet, since they have sizes close to the carbon atom size. The synthesis and the study of the properties of graphene doped with 3p elements are complex.

The two-dimension crystal structure of graphene makes it possible to vary its properties by the implantation of various materials; i.e., impurities and defects influence the material characteristics. Impurities of 4p elements, in particular, germanium and silicon can impart semiconductor properties to graphene. The properties of graphene containing germanium have attracted still less attention [13–16] than the properties of graphene containing 2p and 3p elements of the periodic system. Taking into account the abovementioned, we consider the results of the works, in which the influence of Ge-doping on the graphene properties and structure was studied.

The results of studies of the influence of doping graphene with lithium, silicon, and germanium atoms on its defect structure are presented in [13]. It was shown using the density functional theory that the energy gap of graphene increases in the case of adsorption of lithium on the graphene surface with divacancies. The energy gap width remains unchanged as germanium is added and decreases as silicon is added. The difference between the minimum and maximum energy gap widths is insignificant. Additions of silicon and germanium leads to an increase lithium adsorbtion rate on graphene, which enables one to increase the graphene charge-discharge capacity. Thus, the doped graphene has the high charge-discharge cap-acity.

The adsorption of Si and Ge on graphene was studied in [14] using the density functional theory method. It is shown that Si and Ge atoms are bound with carbon atoms in graphene with a significant binding energy. As a result of adsorption of the analysis of the abovementioned works shows that Si and Ge, the polymetallic graphene becomes metalized and takes a magnetic moment. This effect is due to a combination of adatomic orbitals with the orbitals of the sp2 states of graphene.

In [15], it was found that germanium–graphene nanocomposite has a high Coulomb efficiency (80.4%) in the first cycle and conserves the capacity 84.9% after 400 complete cycles as the anode of an ion-lithium batteries. This nanocomposite can be formed by thermal evaporation of germanium at a low pressure. In this case, crystalline germanium particles are uniformly deposited on the graphene surface with a flexible structure or implanted into graphene vacancies.

In [16], the structure of a monolayer graphene containing implanted germanium ions (74Ge+) was studied using a scanning electron microscope. It is shown that individual 74Ge+ ions are chemically bounded with three nearest neighboring carbon atoms of graphene. Ion 74Ge+ can be also disposed in the divacancies of the graphene structure. Such an interaction makes it possible to implant 74Ge+ ions below the threshold energy of the displacement of carbon atoms in the graphene lattice. The implantation of 74Ge+ ions to the graphene lattice allows one to change the electron, mechanical, and chemical properties of graphene.

The analysis of the abovementioned works shows that such important problems as the controlling physicochemical properties of graphene, its functionalization, the modification of the electronic state of the valence band of graphene having a zero energy gap, the influence of the Si- and Ge-doping on the electron dispersion near the Fermi level and the charge carrier transfer in graphene are scantily known up to now.

One of the known forms of the graphene modification is the covalent functionalization, whose result can be change in the electrical properties of graphene [17]. The removal of a π electron from carbon atom decreases the density of carriers and can lead to the formation of an energy gap. The functionalizing molecule can also generate the energy levels in the band structure of the covalently functionalized graphene, making it a semiconductor of the n- or p-type. A deficit of carriers and a distortion of the plane lattice cause a decrease in the charge carrier mobility in graphene. In graphene, the charge carrier mobility at room temperature is 104–5 × 104 cm2/V s. Compared to such graphene with the effective energy gap ΔEe, g = 0.2 eV, the reduced graphene oxide is characterized by a lower carrier mobility (0.05–200 cm2/V s), the p-type conductivity, and ΔEe, g = 2.0 eV.

The functionalization of graphene leads to the formation of domains. In some functionalized graphenes, for example, graphene oxide, two domains containing regions sp2 and sp3 with a narrow and a wide energy gaps, respectively [18]. The sp2 graphene region has a high conductivity, and the sp3 graphene region has insulating or semiconductor properties. Since the sizes of these domain sizes, their shapes and the potential barriers are different, the charge carrier transfer from one sp2 region to another that is performed due to the hopping conduction with a variable jump distances.

The transition from the semimetallic highly conducting state to an insulator was also observed during hydrogenation of graphene [19]. The electron microscopy shows that the obtained hydrogenated graphene (HGG) crystallizes in the rhombohedral system and has the lattice parameter smaller as compared to that of graphene. The authors of [19] also present the experimental temperature dependence of the HGG resistivity in the log ρ–T –1/3 coordinates. In this case, they are restricted themselves only by the unfounded statement that the hopping conduction with a variable jump distances takes place in HGG. They did not give any quantitative estimates of the physical parameters of the materials under study. However, the determination of the physical regularities of the temperature dependences of the conductivities and the estimation of the parameters of the localized states using the conduction models and the experimental methods are topical problems.

The abovementioned allows us to conclude that the study of the influence of the Ge- and Si-doping on the modification of the electronic properties of graphene by opening and/or widening the graphene energy gap width is a topical problem.

In this work, we study the influence of the Ge- and Si-doping on the electronic and physical properties the 18- and 54-atom supercells of graphene monolayers by the ab initio calculations using the density functional theory (DFT) method in the framework of the generalizaed gradient approximation (GGA). In addition, we will analyze the temperature dependence of the resistivity in the hydrogenated graphene.

2 MODEL AND THE CALCULATION METHOD

The calculations were carried out using the Atomistix Tool Kit (ATK) program [20], in which the spin-polarized density functional theory (spin-polarized DFT) was realized [21–24], using the projected wave function (PAW) and the exchange–correlation Perdew–Burke–Ernzerhof (PBE) functional methods [25].

The calculations were performed for 18- and 54-atom graphene supercells. The spin-polarized DFT method was used with the generalized gradient approximation (GGA) [26]. In addition to the exchange–correlation PBE functional, we used in our calculations the Double Zeta polarized bases. The kinetic cutoff energy was 150 Ry. In the calculations, the initial graphene cell was weakened and optimized with the tolerances in force and stress of 0.01 and 0.01 eV/Å3, respectively.

The quantum-chemical analysis of the electron population of atomic orbitals was carried out by the Mulliken method [27, 28]. We estimated the contributions of various atomic orbitals (AO) to the molecular orbital (MO) in graphene. The electron population of AO was determined as the sum of electrons over all occupied molecular orbitals. To do this, we took into account the diagonal elements of the composed density matrix and the contribution of the “overlap population.” The overlap population of MO between the considered atomic pair (for example, A (carbon) and B (germanium or silicon)) characterizes the products of the off-diagonal elements of the density matrix by the corresponding overlap integrals. The charge on an atom was calculated by Mulliken, using formula

$${{q}_{{\text{A}}}} = {{Z}_{{\text{A}}}} - \sum\limits_a^{({\text{A}})} {\left[ {{{P}_{{aa}}} + \sum\limits_{{\text{B}} \ne {\text{A}}}^{} {\sum\limits_b^{({\text{B}})} {{{P}_{{ab}}}{{S}_{{ab}}}} } } \right],} $$
(1)

where ZA is the number of valence electrons, Paa is the density matrix element, and PabSab is the overlap population of the molecular orbital.

The doping of graphene was performed by the modification of the electronic structure of the graphene supercells, taking into account the pseudopotentials of Ge and Si in the monolayer structure. The structure was simulated by the optimization of the Ge and Si pseudopotentials using the ATK program. The dopant atoms were placed in a unit vacancy in the monolayer, which led to the formation of the energy gap in the graphene monolayer. From the energy point of view, the divacancy in graphene seems likely to be more stable than the unit vacancy. The problem of studying the graphene monolayer and polylayer with a set of defects (vacancies) needs a special consideration.

3 RESULTS AND DISCUSSION

The problems related to the short-range and long-range correlation effects can be overcame using the density functional theory (DFT). DFT is a one-electron approximation and is formally equivalent to the Hartree–Fock equation. In the general form, DFT is described by the following equation

$$\begin{gathered} \left( { - \frac{{{{\hbar }^{2}}}}{{2m}}{{\nabla }^{2}} + V({\mathbf{r}}) + \int {\frac{{\rho (r{\kern 1pt} ')}}{{\left| {r - r{\kern 1pt} '} \right|}}d{\mathbf{r}}{\kern 1pt} '} + {{V}_{{{\text{XC}}}}}[({\mathbf{r}})]({\mathbf{r}})} \right){{\varphi }_{i}}({\mathbf{r}}) \\ = {{\lambda }_{i}}{{\varphi }_{i}}({\mathbf{r}}), \\ \end{gathered} $$
(2)

where \( - \frac{{{{\hbar }^{2}}}}{{2m}}{{\nabla }^{2}}\) is the electron kinetic energy, V(r) is the external electrostatic potential of nuclei (effective one-particle potential), \(\int {\frac{{\rho (r{\kern 1pt} ')}}{{\left| {r - r{\kern 1pt} '} \right|}}d{\mathbf{r}}{\kern 1pt} '} \) is the Coulomb operator that describes the mean Coulomb field generated by electrons, VXC[(r)] is the exchange correlation operatore (xc functional) that is the functional from the total electron density ρ(r), and φi(r) are the molecular orbitals, along which the electron density of the initial many-particle system forms.

The values of λi of the KS (Kohn–Sham) [21] operator are one-electron orbital energies, and its eigenvectors φi(r) characterize the one-electron wave functions. During a theoretical processing, orbitals λi and φi(r) enable one to associate the energy and the wave function with each electron. The one-particle xc-functional enables one to describe the ground state energy of the complete Schrödinger equation for many b-odies.

3.1 3.1. Electron Properties

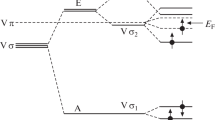
The DFT method allowed us to observe a change in the energy gap width of graphene in the dependence on the type and the concentration of defects or doping elements Si and/or Ge. Figures 1 and 2 shows the band structure of graphene from 18 carbon atoms the band structure of the Si-doped graphene of 18 carbon atoms, respectively.

Fig. 1.
figure 1

Band structure of a graphene supercell of 18 carbon atoms.

Full size image
Fig. 2.
figure 2

Band structure of the Si-doped graphene monolayer of 18 carbon atoms.

Full size image

As one Si atom is substituted for one carbon atom of graphene, the energy gap width (Eg) opens to 0.133 eV. In [29], the different value Eg = 0.02 for a Si-doped graphene monolayer; this value was obtained by another method, namely, by the local density approximation (LDA).

In the case of the Ge-doping, the physicochemical feature of germanium leads to the charge ordering and the opening the energy gap, unlike the case of the Si-doping, at which we observe the separation into macroscopic regions consisting of the charge and magnetic centers.

Thus, it was found by the DFT method that the substitution of Si atom and/or Ge atom for C atom leads to the opening the energy gap in graphene. It is due to the p-states of Si and/or Ge that take part in the hybridization with the carbon p-states. A change in the doping element concentration makes it possible to control the degree of opening of the energy gap in a graphene system. In particular, the Ge-doped graphene without carbon C-vacancy has the energy gap width Eg = 0.505 eV. The inclusion of the vacancy in the Ge-doped graphene gives the energy gap width Eg = 0.21 eV.

The geometric optimization of graphene doped, for example, with Ge shows that the large covalent radius of Ge (r = 1.22 Å) as compared to the radius of C (r = 0.75 Å) distorts the graphene structure. After the structure optimization, the bond distances between atoms are substantially changed. The bond distances between various carbon atoms were varied from 1.53 Å to 1.65 Å (C–Ge).

The many-particle electron interactions between atoms in graphene supecells were analyzed by the expansion of the molecule properties into the contributions of individual atoms. To separate the electronic properties of the graphene systems into atomic contributions, we used the electron density of states (DOS). The electronic structures near the Fermi level for 18‑   and 54-atom graphene supercells containing vacancies and doping Si and/or Ge atoms were calculated with the allowance for the electron populations of the atomic orbitals.

Figures 3, 4 show typical examples of the distributions of the total DOS in the graphene supercell. The curves in Figs. 3, 4 characterize the contributions of the formed charges of each atom and individual electron spins in graphene supercells. The upper curves correspond to electrons with the spin up direction, and the bottom curve, with the spin down direction.

Fig. 3.
figure 3

Total electron density of states (DOS) in the Ge-doped graphene supercell with a vacancy containing 18 carbon atoms. A zero energy is taken at the Fermi level; the upper half-panel describes the state with a high spin, and the lower half-panel, with lower spin.

Full size image
Fig. 4.
figure 4

Total electron density of states (DOS) in the Ge-doped graphene supercell with a vacancy containing 54 carbon atoms. A zero energy is taken at the Fermi level; the upper half-panel describes the state with a high spin, and the lower half-panel, with lower spin.

Full size image

The DOS distributions, for example, in the graphene–Ge monolayer demonstrate the formation of new electronic states near the Fermi level. This fact shows that the implantation of germanium atoms in graphene opens the energy gap Eg in graphene. As a result of an increase in Eg, the optical conductivity of the material also increases, The appearance of an energy gap on monolayers of the doped graphene supercells is important for applying graphene in field-effect transistors and spintronics devices.

From the analysis of the electronic structure near the Fermi level, it follows that an antiferromagnetic ordering forms in the graphene monolayer. The gained magnetization in the doped graphene is induced by the interaction of nonhybridized 2p electrons of carbon with unpaired 3p electrons of Si and/or Ge. The antiparallel arrangement of the magnetic moments is a result of the interaction between neighboring carbon atoms in the doped graphene.

The gained magnetic moments have different values and spin directions in the dependence on the binding energy between various atoms of carbon and Si and/or Ge in the graphene supercells. The DOS spectra differ in the energies of peaks of partial DOS due to different degrees of perturbation upon the hybridization of atoms in the doped graphene supercells. The existence of carbon vacancies and atoms of Si and/or Ge in graphene supercells is found to lead, as well, to the spin polarization near the Fermi level and ferromagnetic ordering.

In particular, in the Ge-doped graphene supercell from 54 carbon atoms, for example, 26th carbon atom takes a magnetic moment in the direction that coincides in sign with magnetic moment of the nearest carbon atom. On carbon atom no. 26, the induced magnetic moment is 0.327 μB. Other carbon atoms also have gained magnetic moments in the graphene–Ge system: the third carbon atom (0.326 μB), 9th (0.101 μB), 15th ((0.101 μB), 21th (0.325 μB), and 26th (0.327 μB) in the preferential directions and the carbon atoms 8th (–0.035 μB), 14th (–0.033 μB), 31th (‒0.036 μB), and 49th atom (–0.036 μB) in the opposite direction.

In the Ge-doped graphene supercell containing carbon vacancies, the total magnetic moment is 0.998 μB. In the case of the substitution of Ge atom for carbon atom of graphene and the existence of a C vacancy disposed near Ge, germanium atoms induce the magnetic moment 0.031 μB. The magnetic moment near the vacancy is 0.48 μB.

Th characteristic nanosizes, such as the critical diameter of a magnetic domain, the exchange interaction length, and the spin diffusion length can influence the antiferromagnetic ordering of magnetic nanoparticles [30, 31]. The magnetic domain critical diameter is the largest size, beyond which a domain is energetically stable. The critical diameter of a single-domain particle \(D_{{{\text{cr}}}}^{{{\text{sd}}}}\) varies from 10 nm to several thousand nanometers for various materials.

The value of \(D_{{{\text{cr}}}}^{{{\text{sd}}}}\) is given be the following relationship [31]:

$$D_{{{\text{cr}}}}^{{{\text{sd}}}} = \frac{{72\sqrt {A{{K}_{a}}} }}{{{{\mu }_{0}}M_{s}^{2}}},$$
(3)

where A is exchange stiffness (interaction) constant, Ka is the uniaxial anisotropy constant (Ka > 0), Ms is the saturation magnetization, i.e., the limiting value of the magnetic saturation, μ0 is the magnetic permittivity in vacuum (magnetic constant) that is 4π × 10–7 N/m in the SI system. The estimated critical diameter of the nanoparticles (≤100 nm) of the graphene–Ge supercells is comparable with \(D_{{{\text{cr}}}}^{{{\text{sd}}}}\) of a single-domain magnetic nanoparticle. The sizes of integrated circuits and the grain sizes in magnetic film carriers are in this range.

3.2 3.2. Charge Transfer

The temperature dependence of the resistivity of hydrogenated graphene (HGG) at low temperatures (T = 4–125 K) is given in [19]. We analyzed this dependence in terms of the hopping Mott model [32] and reconstructed in the log σ–T –1/4 coordinates (Fig. 5). As seen from Fig. 5, the experimental points in the Mott coordinates fall well on the same straight line. Such character of the behavior of the conductivity in HGG at low temperatures is inherent in the hopping mechanism of the charge transfer with variable jump distance [33]. In this case, the current is transferred by the charge carriers disposed in the states localized near the Fermi level. The temperature dependence of the hopping conductivity obeys the Mott law [32]

$$\sigma \propto \exp [ - {{({{T}_{0}}{\text{/}}T)}^{{1/4}}}]$$
(4)

with slope

$${{T}_{0}} = \frac{{16}}{{k{{N}_{{\text{F}}}}{{a}^{3}}}},$$
(5)

where NF is the density of localized states near the Fermi level and a is the localization radius of the wave function.

Fig. 5.
figure 5

Low-temperature electrical conductivity of hydrogenated graphene in the Mott coordinates.

Full size image

Thus, the dc conductivity of semiconductors is adequately described using the two following parameters: the density of states at the Fermi level and the localization radius of the wave function. From the slope of the dependence of log σ on T –1/4, we found the value T0 = 2.2 × 103 K. The density of the localized states near the Fermi level in HGG NF = 2 × 1021 eV‒1 cm–3 was found from Eq. (5) using the experimental value of T0. In this case, we used the value of the localization radius a = 35 Å that is characteristic of 2D crystalline materials [1].

The jump distance in hydrogenated graphene (HGG) at low temperatures was determined by the relationship [32]

$$R = \frac{3}{8}a{{({{T}_{0}}{\text{/}}T)}^{{1/4}}}.$$
(6)

So, R = 64 Å at T = 4 K.

The energy spread (ΔE) of trap states near the Fermi level was estimated by formula [33]

$$\Delta E = \frac{3}{{2\pi {{R}^{3}}{{N}_{{\text{F}}}}}},$$
(7)

ΔE = 1 meV. It is the energy band, in which the hopping transfer takes place in the energy gap of HGG. In this case, the average activation energy of jumps (ΔW) in HGG found by formula [34]

$$\Delta W = \frac{{{{{(kT)}}^{{3/4}}}}}{{{{{[{{N}_{{\text{F}}}}{{a}^{3}}]}}^{{1/4}}}}}$$
(8)

at T = 4 K is ΔW = 0.8 meV.

We also estimated the concentration of localized states (Nt) responsible for the dc charge transfer in HGG:

$${{N}_{t}} = {{N}_{{\text{F}}}}\Delta E.$$
(9)

The value of Nt is 2 × 1018 cm–3.

4 CONCLUSIONS

The DFT calculations of the equilibrium atomic and band structures of Ge- and Si-doped supercells of graphene monolayers containing 18 and 54 carbon atoms demonstrate their stability. The implantation of doping Ge and Si in graphene monolayers leads to the opening of the band of the graphene energy gap. In Ge-doped graphene without vacancy, the energy gap width is Eg = 0.505 eV and the inclusion of vacancies gives the value Eg = 0.21 eV. The calculated electron densities of states for the Ge- and Si-doped graphene supercells which characterize the contributions of the formed charges also show the formation of the marked energy gap.

The implantation of Ge and/or Si atoms in graphene supercells is shown to induce local magnetic moments in carbon atoms, i.e., the ferromagnetic state of carbon atoms forms in the modified energy gap of the band structure of the doped graphene. The local magnetic moments on carbon atoms in graphene monolayers demonstrate that they differ from each other and their antiferromagnetic ordering. In the Ge-doped graphene, the gained magnetic moment of carbon, for example, near the carbon vacancy (0.998μB) is higher than that in carbon of the vacancy-free graphene (0.001μB).

At temperatures 4–125 K, the conductivity of the hydrogenised graphene (HGG) correspond to the hopping charge transfer mechanism with a variable jump distance. We found that the density of localized states near the Fermi level is NF = 2 × 1021 eV–1 cm–3. The calculated jump distance in HGG is 64 Å, and the energy spread of the trap states near the Fermi level is ΔE = 1 meV. The value of ΔE agrees with the jump activation energy(ΔW) in HGG that, according to our estimations is ΔW = 0.8 meV. The estimated concentration of localized states is Nt = 2 × 1018 cm–3.