INTRODUCTION

Interaction of high-power laser radiation with dense plasma is accompanied by generation of super-strong quasi-static magnetic fields [1] with a magnitude reaching several hundred MG [2]. Resonance interaction of high-power laser radiation with plasma in such fields leads to excitation of high-amplitude nonlinear plasma oscillations [3–6]. Strong magnetic field can also be induced in plasma in the constriction region of a Z-pinch. Interaction of laser radiation with Z-pinch plasma under resonance conditions can result in nonlinear oscillations of high amplitude [7].

Heating via parametric resonance is widely used in tokamaks and other systems with magnetic plasma confinement [9]. Nonlinear processes in the inhomogeneous region in the vicinity of exact resonance play a crucial role in this kind of heating. They involve a decay of the pumping wave into two upper-hybrid plasmons and excitation of the Bernstein waves [10]. Similar processes should also take place under resonance interaction of a high-power laser radiation with plasma in a strong magnetic field. The mechanism of electron heating by an extraordinary laser wave under the conditions of a fundamental parametric resonance at twice the upper-hybrid frequency in homogeneous plasma was studied in [8]. In the present work, we studied such processes by means of numerical simulation in the region of resonance in inhomogeneous plasma.

NUMERICAL SIMULATION OF PARAMETRIC RESONANCE IN INHOMOGENEOUS PLASMA

Let an extraordinary electromagnetic wave E = (Ex, 0, Ez), B = (0, By, 0) be propagating in inhomogeneous plasma perpendicular to static external magnetic field B0 = (0, B0, 0). We assume that the initial density of plasma monotonically increases along the direction of wave propagation. We also assume that the condition of parametric resonance at frequency ω0 = 2ωuh, where ω0 is the (angular) frequency of the wave, ωuh = \(\sqrt {\omega _{p}^{2} + \omega _{c}^{2}} \) is the upper hybrid frequency, ωp is the plasma frequency, and ωc is the cyclotron fr-equency, is fulfilled. When conducting a numerical simulation, it is convenient to transform to dimensionless frequencies and dimensionless wave am-plitude in vacuum by introducing the following qua-ntities:

$$\begin{gathered} {{q}_{p}} = \frac{{{{\omega }_{p}}}}{{{{\omega }_{0}}}},\quad {{q}_{c}} = \frac{{{{\omega }_{c}}}}{{{{\omega }_{0}}}},\quad {{q}_{{uh}}} = \frac{{{{\omega }_{{uh}}}}}{{{{\omega }_{0}}}}, \\ \varepsilon = \frac{{e{{E}_{0}}}}{{{{m}_{e}}{{\omega }_{0}}c}}. \\ \end{gathered} $$

We will use the following model distribution of the unperturbed plasma density:

$$N(Z) = n{\text{/}}n({{Z}_{{p0}}}) = 1 + a\tanh \left[ {\frac{{2(Z - {{Z}_{{p0}}})}}{{{{L}_{p}}b}}} \right],$$
(1)

where Z is the dimensionless coordinate in units of \(k_{0}^{{ - 1}}\); k0 is the wavenumber of the laser wave in vacuum; Zp0 is the point at which qp(Z) attains a given value equal to qp; Lp is the dimensionless width of the plasma layer; parameters a and b determine the height and width of the density-drop region, respectively.

Numerical simulation of parametric interaction of a high-power extraordinary wave with plasma was carried out in the present work by means of the relativistic PIC code 1D2V used in [4–6]. In the vacuum region, radiation was assumed to be propagating along the z axis in the direction of a plasma layer exhibiting model density distribution (1). Initially, the pulse had the shape of a plane wave with smooth leading and trailing edges. The pulse width in the numerical simulations was assumed to be equal to 100 cycles of the wave field. The initial width of the plasma layer was equal to 80 initial laser wavelengths. Calculations were carried out for the ion-to-electron mass ratio of mi/me = 1840.

Ions had little effect on the process of interaction during the time of pulse propagation through the plasma layer. Physical parameters were chosen close to those used in [7]. It was assumed that an extraordinary wave at the fourth-harmonic frequency of the fundamental radiation that had a wavelength of 1064 nm was incident on the plasma layer. In the course of simulation, it was assumed that the dimensionless amplitude of the fourth harmonic could reach the magnitude of \(\varepsilon \approx 0.1\), similar to [8]. Such amplitudes can be obtained only by using crystals for nonlinear frequency conversion exhibiting exceptionally high characteristics. At plasma density of 1021 cm–3, plasma frequency for the fourth harmonic corresponds to qp ≈ 0.3. The dimensionless cyclotron frequency qc was varied between 0.1 and 0.2, which corresponds to magnetic fields between 40 and 80 MG.

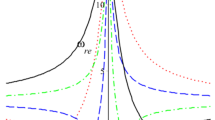
Numerical simulations revealed that laser radiation interacting with plasma in a strong magnetic field in the parametric-resonance region imparts considerable part of energy to electrons. Distributions of the longitudinal and transverse fields at the moment of time when the laser pulse reaches the right boundary of the plasma layer are illustrated in Fig. 1.

Fig. 1.
figure 1

Distribution of the longitudinal and transverse fields at time t = 600. The dashed line represents the initial profile of plasma density. ε = 0.1, qp = 0.3, qc = 0.2, Te0 = 1 keV, a = 0.8, b = 0.1, Zp0 = 950, Zb = 800.

Full size image

It can be seen that the transverse electric field Ex of the pulse experiences strong absorption in the region of parametric upper-hybrid resonance, while the amplitude of the longitudinal field Ez grows. It can also be seen that there appears a reflected electromagnetic wave at half the incident-radiation frequency. Supposedly, these processes are caused by the decay of the laser wave into two upper-hybrid plasmons. A similar process takes place under electron cyclotron heating in tokamaks [9, 10]. The growth of the longitudinal field can be caused by interaction of such plasmons with nonlinear electrostatic modes similar to the Bernstein modes in the linear approximation. These considerations are corroborated by the corresponding spectra of the longitudinal electric field presented in Fig. 2.

Fig. 2.
figure 2

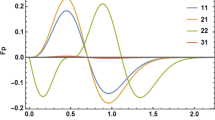
Spectra of longitudinal field Ez (arbitrary units) at time t = 600 at point Z = 930. (a) Te0 = 0, (b) Te0 = 1 keV. Other parameters are the same as in Fig. 1.

Full size image

It can be seen that the spectra clearly reveal the lines with frequencies close to ω0/2 corresponding to the upper-hybrid plasmons. The spectra of heated plasma contain lines with frequencies in the vicinity of the cyclotron frequency (Fig. 2). Since they disappear at the same parameters in cold plasma, they can be interpreted as being the nonlinear Bernstein modes driven at high pump amplitudes. The growth of the longitudinal field causes substantial heating of the electron component. The process of heating can be clearly seen in the phase planes of electrons presented in Fig. 3. The dependence of the average energy of electrons in the process of their heating on initial electron temperature was also studied in the numerical experiments (Fig. 4). It can be seen that the efficiency of heating considerably increases with increase in the initial temperature, which is related to growth of amplitudes of the Bernstein waves.

Fig. 3.
figure 3

Phase planes of electrons at time t = 600. Values of parameters are the same as in Fig. 1.

Full size image
Fig. 4.
figure 4

Average energy of electrons at time t = 600 as a function of initial temperature. Parameters are the same.

Full size image

CONCLUSIONS

We conducted numerical simulation of interaction of an extraordinary laser wave with inhomogeneous plasma in the region of parametric resonance at twice the upper-hybrid frequency. Numerical experiments revealed that the pumping wave decays into two upper-hybrid plasmons in this case, and this process is accompanied by excitation of electrostatic oscillations representing nonlinear Bernstein waves. Interaction of these oscillations leads to considerable heating of electrons. In the process, the efficiency of heating increases with increase in the initial electron temperature. The average energy of electrons reaches 5 keV for initial temperatures on the order of 1 keV.

Similar processes take place also in the case of electron cyclotron heating in plasma systems with magnetic confinement [11]. However, the amplitudes of the microwave radiation in such processes are several orders of magnitude lower than the amplitudes of the laser radiation. The same is true for the magnitudes of the corresponding magnetic fields under resonance conditions. Therefore, the results of interaction in these two cases can substantially differ from one another due to the influence of the nonlinear and relativistic effects. Numerical simulation of the laser parametric heating was conducted in the present work in order to clarify these differences.