On a Signature of Phase Transition in Heavy Ion Nuclear Matter

Abstract

Some results of data analysis of hadron production in $p + p$ and $A + A$ collisions obtained in the framework of $z$-scaling are discussed. A possible signature of phase transition in the matter created in central ${\text{Au}} + {\text{Au}}$ collisions in the scaling regime is observed. The concept of the $z$-scaling is based on the principles of self-similarity, locality and fractality of particle interactions at a constituent level. The self-similarity variable $z$ and the scaling function $\psi (z)$ are expressed via the experimentally measurable quantities and some model parameters characterizing the structure of colliding objects, fragmentation process and specific heat of the produced medium. The irregularities of fractal entropy and specific heat parameter ${{c}_{{{\text{AuAu}}}}}$ observed in $K_{S}^{0}$-meson production in ${\text{Au}} + {\text{Au}}$ collisions at RHIC are considered as an indication of phase transition in nuclear matter.

INTRODUCTION

Search for signature of phase transition and location of a critical point on the phase diagram of the nuclear matter are main goals of heavy ion programs performed at SIS, SPS, RHIC and LHC (see [1] and references therein).

Different signatures of critical phenomena for non-nucleus systems are known. Among them there are increase in compressibility (liquid-vapor equilibrium), increase in magnetic and dielectric susceptibility in the vicinity of the Curie points of ferromagnets and ferroelectrics, anomaly in heat capacity at the point of transition of helium to the superfluid state, slowing of the mutual diffusion of substances near the critical points of mixtures of stratifying liquids, anomaly in the propagation of ultrasound (absorption of sound and an increase in its dispersion), anomalies in viscosity, thermal conductivity, slowdown in the establishment of thermal equilibrium, etc. These anomalies are described by power laws with critical indices.

The concepts of “scaling” and “universality” have been developed and widely used to explain the critical phenomena [2, 3]. Scaling implies that systems near critical points exhibit self-similarity and are invariant with respect to scale transformations. The universality of their behavior lies in the fact that vastly different systems behave in a similar way near respective critical points which is usually described by a power dependence. The notions of scaling and universality have also been applied for particle production far from the boundary of a phase transition or a critical point. In high energy collisions, the scaling regularities were subject of intense investigations.

One of the fundamental principles governing hadron interactions at high energies is the self-similarity principle. Scaling behaviour based on the ideas of self-similarity of hadron interactions at the constituent level is manifested by the $z$-scaling [4–6]. The scaling was used for analysis of inclusive spectra obtained at the accelerators U70, ${\text{S}}\bar {p}pS$, SPS, ISR, Tevatron, and RHIC. The transverse momentum spectra reveal striking similarity over a wide range of energies when expressed by the variable $z$. The $z$-scaling is considered as a manifestation of the self-similarity of the structure of colliding objects (hadrons or nuclei), the interaction mechanism of their constituents, and the process of fragmentation into real hadrons. The universality of the scaling is given by its flavour independence. This means that the spectra of particles with different flavour content can be described by the same function $\psi (z)$ with values of $z$ and $\psi$ rescaled by a factor ${{\alpha }_{{\text{F}}}}$. The method of $z$-scaling in proton-(anti)proton collisions was used in analyses of spectra of different hadrons including heavy quarkonia and top quark. The hypothesis of self-similarity and fractality of hadron interactions in relativistic collisions of heavy nuclei was tested using $z$-presentation of spectra of charged hadrons and pions.

In the paper we discuss the possible signatures of a phase transition in heavy ion nuclear matter in the framework of the $z$-scaling concept.

$z$-SCALING

We assume that at high energy, the collisions of ${{A}_{1}}$ and ${{A}_{2}}$ nuclei can be expressed by the interactions of their constituents. The momentum distribution of a produced inclusive particle $h$ in the process ${{A}_{1}} + {{A}_{2}} \to h + X$ is described in terms of a binary collision of the constituents with masses ${{x}_{1}}{{M}_{1}}$ and ${{x}_{2}}{{M}_{2}}$. The quantities ${{x}_{1}}$ and ${{x}_{2}}$ are the momentum fractions carried by the interacting constituents of the incoming nuclei with masses ${{M}_{1}}$ and ${{M}_{2}}$ and 4-momenta ${{P}_{1}}$ and ${{P}_{2}}$, respectively. It is also assumed that the objects with masses ${{{{m}_{a}}} \mathord{\left/ {\vphantom {{{{m}_{a}}} {{{y}_{a}}}}} \right. \kern-0em} {{{y}_{a}}}}$ and $({{x}_{1}}{{M}_{1}} + {{x}_{2}}{{M}_{2}} + {{{{m}_{b}}} \mathord{\left/ {\vphantom {{{{m}_{b}}} {{{y}_{b}}}}} \right. \kern-0em} {{{y}_{b}}}})$ are produced in the scattered and recoil directions in such a collision. The ${{y}_{a}}$ and ${{y}_{b}}$ represent the corresponding momentum fractions carried by the inclusive particle with mass ${{m}_{a}}$ and its hadron counterpart with mass ${{m}_{b}}$ moving in opposite direction. The momentum conservation law in the binary collision gives the following condition:

$${{({{x}_{1}}{{P}_{1}} + {{x}_{2}}{{P}_{2}} - {p \mathord{\left/ {\vphantom {p {{{y}_{a}}}}} \right. \kern-0em} {{{y}_{a}}}})}^{2}} = M_{X}^{2}.$$

(1)

The recoil mass is in the form ${{M}_{X}} = {{x}_{1}}{{M}_{1}} + {{x}_{2}}{{M}_{2}} + {{{{m}_{b}}} \mathord{\left/ {\vphantom {{{{m}_{b}}} {{{y}_{b}}}}} \right. \kern-0em} {{{y}_{b}}}}$. The produced particle with mass ${{m}_{b}}$ ensures the conservation of additive quantum numbers.

Using the scenario of binary constituent interactions, we also assume that the inclusive hadron production has the property of self-similarity. The self-similarity of hadron interactions at a constituent level is studied by the variable $z$ defined as follows

$$z = {{z}_{0}}{{\Omega }^{{ - 1}}},$$

(2)

where ${{z}_{0}}{{ = \sqrt {{{s}_{ \bot }}} } \mathord{\left/ {\vphantom {{ = \sqrt {{{s}_{ \bot }}} } {[{{{({{d{{N}_{{{\text{ch}}}}}} \mathord{\left/ {\vphantom {{d{{N}_{{{\text{ch}}}}}} {{{{\left. {d\eta } \right|}}_{{\eta \approx 0}}}}}} \right. \kern-0em} {{{{\left. {d\eta } \right|}}_{{\eta \approx 0}}}}})}}^{c}}{\kern 1pt} {{m}_{N}}]}}} \right. \kern-0em} {[{{{({{d{{N}_{{{\text{ch}}}}}} \mathord{\left/ {\vphantom {{d{{N}_{{{\text{ch}}}}}} {{{{\left. {d\eta } \right|}}_{{\eta \approx 0}}}}}} \right. \kern-0em} {{{{\left. {d\eta } \right|}}_{{\eta \approx 0}}}}})}}^{c}}{\kern 1pt} {{m}_{N}}]}}.$ The variable ${{z}_{0}}$ is proportional to the transverse kinetic energy, $\sqrt {{{s}_{ \bot }}}$, of a selected constituent sub-process consumed on the production of the inclusive particle with mass ${{m}_{a}}$ and its counterpart with mass ${{m}_{b}}$. The quantity ${{d{{N}_{{{\text{ch}}}}}} \mathord{\left/ {\vphantom {{d{{N}_{{{\text{ch}}}}}} {{{{\left. {d\eta } \right|}}_{{\eta \approx 0}}}}}} \right. \kern-0em} {{{{\left. {d\eta } \right|}}_{{\eta \approx 0}}}}}$ is the corresponding (pseudorapidity) multiplicity density of charged particles produced in the reaction central region at the mid-rapidity, $\eta \approx 0$. The multiplicity density is related to a state of the produced medium. The parameter $c$ characterizes the properties of this medium. The constant ${{m}_{N}}$ is fixed at the value of the nucleon mass. The symbol $\Omega$ stands for the maximum of the function,

$$\Omega = {{(1 - {{x}_{1}})}^{{{{\delta }_{1}}}}}{{(1 - {{x}_{2}})}^{{{{\delta }_{2}}}}}{{(1 - {{y}_{a}})}^{{{{\epsilon }_{a}}}}}{{(1 - {{y}_{b}})}^{{{{\epsilon }_{b}}}}}$$

(3)

under the kinematic constraint (1). This quantity connects the momentum fractions defining kinematics of a selected binary collision at a microscopic level with the structural and fragmentation characteristics of the reaction. The structure of the colliding hadrons/nuclei and fragmentation of the objects produced in the binary collisions of their constituents are described by ${{\delta }_{1}},{{\delta }_{2}}$ and ${{\epsilon }_{a}},{{\epsilon }_{b}}$, respectively. These parameters are interpreted as fractal dimensions. The quantity $\Omega$ is proportional to the relative number of all such configurations in the inclusive process, which contain a state defined by the fractions ${{x}_{1}},{{x}_{2}},{{y}_{a}},$ and ${{y}_{b}}$. For given values of ${{\delta }_{1}}$, ${{\delta }_{2}}$, ${{\epsilon }_{a}}$, and ${{\epsilon }_{b}}$, the selected sub-process is singled out of all constituent sub-processes by the values of the momentum fractions ${{x}_{1}}$, ${{x}_{2}}$, ${{y}_{a}}$, and ${{y}_{b}}$, which maximize the function $\Omega ({{x}_{1}},{{x}_{2}},{{y}_{a}},{{y}_{b}})$ under condition (1). The quantity ${{\Omega }^{{ - 1}}}$ characterizes a resolution at which the selected sub-process is singled out of the inclusive reaction. The value of ${{z}_{0}}$ is proportional to $\sqrt {{{s}_{ \bot }}}$ in the selected sub-process consumed on the production of the inclusive particle with mass ${{m}_{a}}$ and its counterpart with mass ${{m}_{b}}$.

The scaling function $\psi (z)$ is expressed in terms of the experimentally measured inclusive invariant cross section, the (pseudorapidity) multiplicity density, ${{dN} \mathord{\left/ {\vphantom {{dN} {d\eta }}} \right. \kern-0em} {d\eta }}$, and the total inelastic cross section, ${{\sigma }_{{{\text{in}}}}}$, as follows:

$$\psi (z) = \pi ({{dN} \mathord{\left/ {\vphantom {{dN} {d\eta }}} \right. \kern-0em} {d\eta }}){{\sigma }_{{{\text{in}}}}}{{J}^{{ - 1}}}E{{d}^{3}}\sigma d{{p}^{3}},$$

(4)

where $J$ is the Jacobian of the transformation from $\{ p_{T}^{2},y\}$ to $\{ z,\eta \}$ pairs of variables. The multiplicity density concerns particular hadrons species. The integral of $\psi (z)$ over the interval $(0,\infty )$ is normalized to unity. It allows the interpretation of the scaling function as a probability density to produce the inclusive particle with the corresponding $z$-value.

p + p COLLISIONS

Data for $p + p$ interactions are usually used as a reference for comparison with $p + A$ and $A + A$ collisions. The $z$-scaling of inclusive hadron production in $p + p$ interactions was established [4–6] from transverse momentum spectra measured at the FNAL, CERN, and BNL energies.

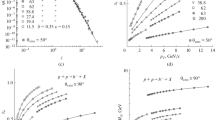
The scaling function $\psi (z)$ decreases by more than ten orders of magnitude with the increasing $z$ in a large ${{p}_{{\text{T}}}}$-range. The energy independence of $\psi (z)$ gives strong constrains on the values of model parameters. For symmetric $p + p$ collisions we have ${{\delta }_{p}} \equiv {{\delta }_{1}} = {{\delta }_{2}}$. We also suppose a particle-(anti)particle production with ${{\epsilon }_{{\text{F}}}} \equiv {{\epsilon }_{a}} = {{\epsilon }_{b}}$, where $F$ denotes flavor dependence. The $z$-scaling is consistent with the constant values of the parameters ${{c}_{{pp}}} = 0.25$, ${{\delta }_{p}} = 0.5$, and ${{\epsilon }_{{{{h}^{ - }}}}} = 0.2$ for $\sqrt s \gtrsim 19$ GeV. At the energy $\sqrt s =$ 11.5 GeV, the scaling regularity indicates a decrease of the fractal dimensions ${{\delta }_{p}}$ and ${{\epsilon }_{F}}$ resulting from a smearing of fractality at low $\sqrt s$. The form of $\psi (z)$ can be described by a power law, $\psi (z) \sim {{z}^{{ - \beta }}}$, in the asymptotic high-$z$ (high-${{p}_{{\text{T}}}}$) region. A saturation of the scaling function is found at low $z$ (low ${{p}_{{\text{T}}}}$) both for negative hadrons and identified particles.

The momentum fraction ${{x}_{1}}$ and ${{x}_{2}}$ characterize energy of the constituent sub-process. They demonstrate characteristic monotonic growth with ${{p}_{{\text{T}}}}$ and a decrease with the increasing collision energy $\sqrt s$. The relative energy loss ${{\Delta {{E}_{q}}} \mathord{\left/ {\vphantom {{\Delta {{E}_{q}}} {{{E}_{q}}}}} \right. \kern-0em} {{{E}_{q}}}} = (1 - {{y}_{a}})$ of the scattered constituent with energy ${{E}_{q}}$ associated with a high-${{p}_{{\text{T}}}}$ particle is smaller than for the inclusive particle with lower transverse momentum. For a given ${{p}_{{\text{T}}}}$, the energy loss is larger at higher collision energy, as the corresponding fraction ${{y}_{a}}$ decreases with $\sqrt s$. The recoil mass ${{M}_{X}}$ characterizing the recoil object in the corresponding sub-process reveals growth at low ${{p}_{{\text{T}}}}$, followed by a successive flattening and an increase with $\sqrt s$. The parameter $c$ controls the multiplicity independence of the scaling function. The obtained results for ${{h}^{ - }}$-hadron production in $p + p$ collisions give us no indications on violation of the $z$-scaling and confirm the self-similarity of constituent interaction over a wide kinematic range.

The scaling properties of strangeness production in $p + p$ collisions confirm self-similarity of hadron production at constituent level. We analysed spectra of strange mesons $(K_{S}^{0},{{K}^{ - }},{{K}^{{*0}}}$ and $\phi )$ measured by the STAR and PHENIX collaborations at RHIC in the framework of $z$-scaling [6]. Results of the analysis are compared with other data on meson and hyperon spectra obtained at RHIC, ISR, SPS, and Tevatron.

The corresponding fragmentation dimension ${{\epsilon }_{{\text{F}}}}$ for strange mesons was determined to be larger than for pions, suggesting larger energy loss by production of mesons with strangeness content. The fragmentation dimension for strange baryons grows with the number of the strange valence quarks. This is connected with the increase of energy losses. The energy independence of $\psi (z)$ over the analyzed kinematic range for strange particles was found at the constant values of the parameters ${{\delta }_{p}} = 0.5,{{c}_{{pp}}} = 0.25$.

Based on performed analyses we conclude that data on non-identified negative hadrons and strange mesons produced at RHIC and SPS support the universality of the scaling function $\psi (z)$ in $p + p$ collisions and constancy of the model parameters ${{\delta }_{p}}$, ${{\epsilon }_{{\text{F}}}}$ and ${{c}_{{pp}}}$. The obtained results are treated as a manifestation of the self-similarity of fractal structure of the colliding protons, interaction mechanism of their constituents, and processes of fragmentation into real hadrons (including hadrons with strange valence quarks). Similar scaling properties were found for other flavors, including production of particles $\Lambda$, $D$, ${J \mathord{\left/ {\vphantom {J \psi }} \right. \kern-0em} \psi }$, $B$, $\Upsilon$, and top quark [4]. The properties of data $z$-presentation are characterized by the energy, angular and multiplicity independence of the scaling function over a large range of kinematic variables.

A + A COLLISIONS

Results of analysis of negative particle spectra measured by the STAR Collaboration in the RHIC BES-I program for ${\text{Au}} + {\text{Au}}$ collisions over a wide range of the collision energy $\sqrt {{{s}_{{NN}}}} = 7.7{\kern 1pt} - {\kern 1pt} 200$ GeV and transverse momentum ${{p}_{{\text{T}}}} = 0.2{\kern 1pt} - {\kern 1pt} 12$ GeV/c of produced particles at different centralities in the central pseudo-rapidity range $\left| \eta \right| < 0.5$ support properties of data $z$‑presentation found in our analyses of spectra of inclusive particles produced in proton-proton collisions [4, 7]. Among them there are energy and flavor independence of the scaling function $\psi (z)$ and universality of its shape for hadron production over a wide kinematic range.

For ${\text{Au}} + {\text{Au}}$ collisions, the scaling variable depends on the parameters ${{\delta }_{{{\text{Au}}}}}$ and ${{\epsilon }_{{{\text{AuAu}}}}}$, which characterize the fractal structure of the colliding nuclei and fractal behavior of the fragmentation processes in the final state, respectively. The third parameter, ${{c}_{{{\text{AuAu}}}}}$, is interpreted as a “specific heat” of the produced medium. It was found that the $z$-scaling is consistent with ${{c}_{{{\text{AuAu}}}}} = 0.11$ and ${{\delta }_{A}} = 0.5A$, where A is mass number of the gold nuclei. The fragmentation dimension ${{\epsilon }_{{{\text{AuAu}}}}}$ increases with multiplicity density. Under such assumptions, the shape of the scaling function is independent of energy and centrality of collisions and is the same as for $p + p$ interactions.

Larger values of ${{\epsilon }_{{{\text{AuAu}}}}}$ in the central collisions reflect larger relative energy losses ${{\Delta E} \mathord{\left/ {\vphantom {{\Delta E} E}} \right. \kern-0em} E}$ as compared to $p + p$ interactions. This implies larger energies of constituent collisions and larger recoil masses ${{M}_{X}}$, which grow with increasing collision centrality and ${{p}_{{\text{T}}}}$. This scenario allows us to interpret the obtained results as a formation of self-similar fractal-like objects in the dense medium created in collisions of heavy nuclei. The obtained results give us clear evidence on self-similarity and fractality of negative hadron production in heavy ion collisions, but no indication on signatures of phase transition.

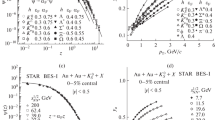
Results of analysis of $K_{S}^{0}{\text{ - }}$meson spectra in ${\text{Au}} + {\text{Au}}$ collisions measured by the STAR Collaboration in the first phase of the Beam Energy Scan program at RHIC confirmed [8] the same scaling behavior of the spectra in $z$-presentation over a wide range of kinematic variables. The result is interpreted as confirmation of self-similarity of fractal structure of nuclei and fragmentation processes with $K_{S}^{0}$ probe. Onset of constant ${{\delta }_{{{\text{Au}}}}}$, smooth increase of ${{\epsilon }_{{{\text{AuAu}}}}}$ and anomalous behavior of ${{c}_{{{\text{AuAu}}}}}$ with collision energy in the scaling regime were found.

For $K_{S}^{0}{\text{ - }}$meson probe, a strong change with collision energy of the specific heat parameter ${{c}_{{{\text{AuAu}}}}}$ was observed. It is approximately equal to 0.16 at $\sqrt {{{s}_{{NN}}}} = 7.7$ and 11.5 GeV. Its value decreases abruptly as a function of the collision energy to about 0.10 at $\sqrt {{{s}_{{NN}}}} = 39$ GeV. In contrast to its constant dependence on $\sqrt {{{s}_{{NN}}}}$ for negative hadrons, the specific heat parameter ${{c}_{{{\text{AuAu}}}}}$ shows an anomaly characterized by a rapid drop in the energy range $\sqrt {{{s}_{{NN}}}} = 11.5{\kern 1pt} - {\kern 1pt} 39$ GeV for $K_{S}^{0}$ mesons. The established behavior is consistent with the energy and centrality independence of the scaling function. The observed anomaly in the specific heat parameter is connected with irregularities of fractal entropy for production of $K_{S}^{0}$ mesons in central ${\text{Au}} + {\text{Au}}$ collisions.

FRACTAL ENTROPY

Boltzmann introduced entropy as a measure of the number of microscopic arrangements or states that comply with the macroscopic condition of the system, which in dimensionless units is expressed as follows

$$S = \ln {{W}_{S}}.$$

(5)

There is a deep connection between the scaling variable and entropy [9, 10]. In the $z$-scaling approach, the quantity ${{W}_{S}} = W{{W}_{0}}$ is the number of all parton and hadron configurations in the initial and final states of the colliding system that can contribute to the production of an inclusive particle with a given momentum $p$. The entropy of fractal configurations used in the definition of the variable $z$ is expressed as follows [11]:

$$\begin{gathered} {{S}_{{\delta ,\epsilon }}} = c\ln \left[ {{{d{{N}_{{{\text{ch}}}}}} \mathord{\left/ {\vphantom {{d{{N}_{{{\text{ch}}}}}} {{{{\left. {d\eta } \right|}}_{0}}}}} \right. \kern-0em} {{{{\left. {d\eta } \right|}}_{0}}}}} \right] \\ + \,\,\ln [{{(1 - {{x}_{1}})}^{{{{\delta }_{1}}}}}{{(1 - {{x}_{2}})}^{{{{\delta }_{2}}}}}{{(1 - {{y}_{a}})}^{{{{\epsilon }_{a}}}}}{{(1 - {{y}_{b}})}^{{{{\epsilon }_{b}}}}}] + \ln {{W}_{0}}. \\ \end{gathered} $$

(6)

The pseudorapidity multiplicity density ${{d{{N}_{{{\text{ch}}}}}} \mathord{\left/ {\vphantom {{d{{N}_{{{\text{ch}}}}}} {{{{\left. {d\eta } \right|}}_{0}}}}} \right. \kern-0em} {{{{\left. {d\eta } \right|}}_{0}}}}$ of the produced charged particles in the central interaction region ($\eta = 0$) characterizes temperature of created matter. The parameter $c$ has meaning of a specific heat of the produced medium. The ${{x}_{1}}$ and ${{x}_{2}}$ are momentum fractions of the colliding ions carried by the interacting constituents. The constituent interaction results in the production of fragmenting objects which are moving in the scattered and recoil direction. The ${{y}_{a}}$ and ${{y}_{b}}$ are the momentum fractions of the produced objects that carry the inclusive particle and its recoil counterpart (antiparticle), respectively. The entropy of the corresponding fractal configurations (6) was named the fractal entropy [11]. It reflects fractal character of the colliding nuclei and fractal nature of the fragmentation processes characterised by the respective fractal dimensions $\delta$ and $\epsilon$.

Properties of the fractal entropy were studied for negative particles, pions, and also for strange neutral mesons. A non-monotonic growth of the entropy ${{S}_{{\delta ,\epsilon }}}$ with energy was found [8] for the transverse momenta ${{p}_{{\text{T}}}} < 1$ GeV/c of $K_{S}^{0}$ mesons produced in the central ${\text{Au}} + {\text{Au}}$ collisions (see Fig. 1). This feature corresponds to the region $\sqrt {{{s}_{{NN}}}}$ = 11–39 GeV. The observed decrease of ${{S}_{{\delta ,\epsilon }}}$ with $\sqrt {{{s}_{{NN}}}}$ is interpreted as a freeze-out of some degrees of freedom in the produced nuclear matter. Such fall in entropy is characteristic for a transition from the “gas” phase, considered at the constituent level at low $\sqrt {{{s}_{{NN}}}}$, to the “liquid” phase at higher energy. The subsequent increase of ${{S}_{{\delta ,\epsilon }}}$ with energy reflects growth of the number of micro-states. This corresponds to the increase of the entropy of the strongly coupled QCD “liquid” phase.

Fig. 1.

The dependence of the entropy (6) on energy $\sqrt {{{s}_{{NN}}}}$ for $K_{S}^{0}{\text{ - }}$meson transverse momentum ${{p}_{{\text{T}}}} =$ 0.3, 0.7, 1.0, 1.5, 2.0, and 3.0 GeV/c in $0{\kern 1pt} - {\kern 1pt} 5\%$ central ${\text{Au}} + {\text{Au}}$ collisions in the rapidity interval $\left| y \right| < 0.5$ [8].

The principle of maximal entropy ${{S}_{{\delta ,\epsilon }}}({{x}_{1}},{{x}_{2}},{{y}_{a}},{{y}_{b}})$ with respect to all constituent sub-processes taking into account 4-momentum conservation in the form (1) is used to determine the momentum fractions ${{x}_{1}}$, ${{x}_{2}}$ ${{y}_{a}}$, and ${{y}_{b}}$. As a result, new conservation law

$${{\delta }_{1}}\frac{{{{x}_{1}}}}{{1 - {{x}_{1}}}} + {{\delta }_{2}}\frac{{{{x}_{2}}}}{{1 - {{x}_{2}}}} = {{\epsilon }_{a}}\frac{{{{y}_{a}}}}{{1 - {{y}_{a}}}} + {{\epsilon }_{b}}\frac{{{{y}_{b}}}}{{1 - {{y}_{b}}}}$$

(7)

was found [9] The conserved quantity—fractal cumulativity—has the form

$$C(D,\zeta ) = D\frac{\zeta }{{1 - \zeta }},$$

(8)

where $D$ is a fractal dimension and $\zeta$ is the corresponding momentum fraction. The conservation law is formulated as follows: The fractal cumulativity before a constituent interaction is equal to that after a constituent interaction for any binary constituent sub-process. We assume that at constituent level every physical particle is a structural object, particle’s constituents possess fractal structure, fragmentation is a fractal-like process, whereas compactness of the fractal structures is governed by the Heisenberg uncertainty principle.

Fractal cumulativity $C(D,\zeta )$ is a property of a fractal-like object (or fractal-like process) with fractal dimension $D$ to form a local compact structural aggregate—a FRACTALON, which carries the fraction $\zeta$ of momentum of its parent fractal. The notion of fractalon typical for particle production at high energy and extremely small scales has similar meaning than that [12] considered in connection with the universality of fractal structures of spacetime at small and cosmologically large scales areas. The authors of [12] define fractalon as a quantum mechanical corpuscule (particle) moving on fractal paths. They consider it may be one or a small cluster of stochastic elements constituting the particle. In such considerations, the fractalon is a free particle conned to move on a fractal trajectory.

CONCLUSIONS

Numerous STAR data on transverse momenta of inclusive spectra of hadrons produced in $p + p$ and ${\text{Au}} + {\text{Au}}$ collisions at RHIC were analyzed in the $z$‑scaling approach. Self-similarity of hadron production over a wide kinematic and centrality range was found. The universality of $\psi (z)$ versus $z$ gives strong restriction on the values of model parameters—fractal dimensions and specific heat ${{c}_{{{\text{AuAu}}}}}$, and allows us to determine their dependence on collision energy, centrality and transverse momentum.

Anomalous behavior of the fractal entropy ${{S}_{{\delta ,\epsilon }}}$ for $K_{S}^{0}$-meson production in the central ${\text{Au}} + {\text{Au}}$ collisions at low ${{p}_{{\text{T}}}}$ in the region $\sqrt {{{s}_{{NN}}}} = 27 - 39$ GeV was found. This is connected with an abrupt change of the specific heat parameter ${{c}_{{{\text{AuAu}}}}}$ observed in the same energy region. The anomaly in the fractal entropy and change of specific heat as a signature of phase transition of nuclear matter produced in heavy ion collisions was discussed. Based on the obtained results we can formulate possible signatures of phase transition in nuclear matter. These are discontinuity or abrupt change of the specific heat parameter $c$, fractal dimensions—$\delta ,\epsilon$, enhancement of $c{\kern 1pt} - {\kern 1pt} \delta {\kern 1pt} - {\kern 1pt} \epsilon$ correlations and anomalous behavior (decrease) of the fractal entropy ${{S}_{{\delta ,\epsilon }}}$ at some selection criteria of events and types of inclusive particles.

The conservation of the fractal cumulativity $C(D,\zeta )$ as a consequence the maximum entropy ${{S}_{{\delta ,\epsilon }}}$ with kinematic constraint was shown. The fractal cumulativity at extremely small scales was interpreted in terms of fractalon—particle moving on fractal trajectories.