INTRODUCTION

Heavy quarkonia have been objects of intense study since the 70s of the last century, when the \({J \mathord{\left/ {\vphantom {J \psi }} \right. \kern-0em} \psi }\) meson was discovered. The calculation of quarkonium production cross sections can be conducted within the framework of the perturbation theory of quantum chromodynamics (QCD) due to the smallness of the strong coupling constant on a scale equal to the mass of the heavy quark, \({{\alpha }_{{\text{S}}}} = 0.2 \sim 0.3\). The process of hadronization of quarks has a nonperturbative nature and can be described within the framework of the approach of nonrelativistic quantum chromodynamics (NRQCD) [1], which is based on the smallness of the relative quark–antiquark velocity in the bound state. In the color singlet model (CSM) [2], it is assumed that a pair \(c\bar {c}\) is produced with the quantum numbers of a finite quarkonium in a color singlet state. A more phenomenological description of hadronization is given within the framework of the color evaporation model (CEM) [3]. Currently, a large amount of experimental data was accumulated in the production of \({J \mathord{\left/ {\vphantom {J \psi }} \right. \kern-0em} \psi }\) mesons in hadronic interactions at energies from \(\sqrt s = \) 19 GeV to \(\sqrt s = \) 13 TeV. On the other hand, only one measurement of the ground state production cross section of charmonium, the \({{\eta }_{{\text{c}}}}\) meson, was carried out by the LHCb collaboration at the Large Hadron Collider (LHC) [4].

1 PARTON REGGEIZATION APPROACH

High energies corresponding to the Regge limit of QCD (\(\sqrt s \gg \mu \), where μ is the characteristic hard scale) require consideration of the noncollinear dynamics of gluons, which is described by the Balitsky–Fadin–Kuraev–Lipatov (BFKL) evolution equation [5]. In [6] and [7], a parton Reggeization approach (PRA) was proposed, which is based on the effect of amplitude Reggeization in quantum chromodynamics in the high-energy limit of multi-Regge kinematics. In this approach, partons are treated as Reggeons or as Reggeized gluons and quarks.

To work directly with Reggeons, an effective field theory was proposed by Lipatov [8], in which a non-Abelian gauge-invariant action was defined, including the fields of Reggeized gluons and Reggeized quarks. The Feynman rules in effective Lipatov field theory can be constructed by analogy with the standard Feynman rules of QCD using gauge-invariant blocks—effective vertices.

Within the framework of the BFKL formalism, nonintegrated parton distribution functions (nPDFs) of Reggeized gluons and quarks are considered, associated with collinear PDFs by the normalization condition:

$$xf_{{\text{g}}}^{{\text{p}}}(x,{{\mu }^{2}}) = \int\limits_{}^{{{\mu }^{2}}} {\Phi _{{\text{g}}}^{{\text{p}}}(x,t,{{\mu }^{2}})dt} .$$

In PRA, it is assumed that the cross section of the hard hadronic process is factorized as the convolution of the parton cross section with the nPDFs of the Reggeized gluon in the proton [9]:

$$\begin{gathered} d\sigma (p + p \to {{\eta }_{{\text{c}}}} + X) = \int \frac{{d{{x}_{1}}}}{{{{x}_{1}}}} \\ \times \,\,\int \frac{{{{d}^{2}}{{q}_{{{\text{1T}}}}}}}{\pi }\Phi _{{\text{g}}}^{{\text{p}}}({{x}_{1}},{{t}_{1}},{{\mu }^{2}})\int \frac{{d{{x}_{2}}}}{{{{x}_{2}}}}\int \frac{{{{d}^{2}}{{q}_{{{\text{2T}}}}}}}{\pi } \\ \times \,\,\Phi _{{\text{g}}}^{{\text{p}}}({{x}_{2}},{{t}_{2}},{{\mu }^{2}})d\hat {\sigma }(R + R \to {{\eta }_{{\text{c}}}} + X), \\ \end{gathered} $$
(1)

where \({{t}_{1}} = {{\left| {{{q}_{{{\text{1T}}}}}} \right|}^{2}},\) \({{t}_{2}} = {{\left| {{{q}_{{{\text{2T}}}}}} \right|}^{2}},{{x}_{1}}\) and \({{x}_{2}}\) are fractions of proton momentum transferred to Reggeized gluons.

The nPDF can be found within an approach proposed by Kimber, Martin, and Ryskin [10]

$$\begin{gathered} {{\Phi }_{i}}(x,t,{{\mu }^{2}}) = \frac{{{{\alpha }_{{\text{s}}}}(t)}}{{2\pi }}\frac{{{{T}_{i}}(t,{{\mu }^{2}},x)}}{t} \\ \times \,\,\sum\limits_{j = q,\bar {q},g} \int_x^1 dz{{P}_{{ji}}}(z){{{\tilde {f}}}_{j}}\left( {\frac{x}{z},t} \right)\theta (\Delta (t,{{\mu }^{2}}) - z), \\ \end{gathered} $$
(2)

where \(\Delta (t,{{\mu }^{2}}) = \frac{{\sqrt {{{\mu }^{2}}} }}{{\sqrt t + \sqrt {{{\mu }^{2}}} }}\), \({{\tilde {f}}_{i}}(x,{{\mu }^{2}})\) = \(x{{f}_{i}}(x,{{\mu }^{2}})\), \({{P}_{{ji}}}(z)\) are the DGLAP splitting functions, аnd the function \({{T}_{i}}(t,{{\mu }^{2}},x)\) is the Sudakov form factor, satisfying the boundary conditions \({{T}_{i}}(t = 0,{{\mu }^{2}},x) = 0\) and \({{T}_{i}}(t = {{\mu }^{2}},{{\mu }^{2}},x) = 1\). The corresponding formula is given in [11].

2 MECHANISMS OF THE \(c\bar {c} \to {{\eta }_{{\text{c}}}}\) HADRONIZATION

Within the framework of the NRQCD, the wave function in the case of the \({{\eta }_{{\text{c}}}}\) meson production can be represented as a superposition of Fock’s states:

$$\begin{gathered} \left| {{{\eta }_{{\text{c}}}}} \right\rangle = \mathcal{O}({{v}^{0}})\left| {c\bar {c}{{[}^{1}}S_{0}^{{(1)}}]} \right\rangle + \mathcal{O}({{v}^{1}})\left| {c\bar {c}{{[}^{1}}P_{1}^{{(8)}}]g} \right\rangle \\ + \,\,\mathcal{O}({{v}^{2}})\left| {c\bar {c}{{[}^{3}}S_{1}^{{(8)}}]g} \right\rangle + \mathcal{O}({{v}^{2}})\left| {c\bar {c}{{[}^{1}}S_{0}^{{(1,8)}}]gg} \right\rangle + \ldots , \\ \end{gathered} $$
(3)

where the quantum numbers of \(c\bar {c}\) pairs are described by ordinary spectroscopic notions, and superscripts (1, 8) in round brackets denote a singlet or octet color state. Only the first term is included in CSM. The production cross section \({{\eta }_{{\text{c}}}}\) in CSM is factorized via the production cross section of the state \({{[}^{1}}S_{0}^{{(1)}}]\) in hard subprocess (perturbative part) and nonperturbative matrix element (NME) of the transition \(\left\langle {{{\mathcal{O}}^{{{{\eta }_{{\text{c}}}}}}}{{[}^{1}}S_{0}^{{(1)}}]} \right\rangle \) (nonperturbative part):

$$\begin{gathered} \hat {\sigma }(a + b \to c\bar {c}{{[}^{1}}S_{0}^{{(1)}}] \to {{\eta }_{{\text{c}}}}) \\ = \hat {\sigma }(a + b \to c\bar {c}{{[}^{1}}S_{0}^{{(1)}}])\frac{{\left\langle {{{\mathcal{O}}^{{{{\eta }_{c}}}}}{{[}^{1}}S_{0}^{{(1)}}]} \right\rangle }}{6}. \\ \end{gathered} $$
(4)

Amplitudes of quark–antiquark pair production in the states \(^{1}S_{0}^{{(1)}}\) and \(^{3}S_{1}^{{(8)}}\), which are considered in this work, can be written in the form [12]

$$\begin{gathered} \left| {\overline {M{{{(R + R \to \mathcal{H}{{[}^{1}}S_{0}^{{(1)}}])}}^{2}}} } \right| \\ = \frac{2}{9}{{\pi }^{2}}\alpha _{s}^{2}\frac{{\left\langle {{{\mathcal{O}}^{\mathcal{H}}}{{[}^{1}}S_{0}^{{(1)}}]} \right\rangle }}{{{{M}^{3}}}}{{F}^{{{{[}^{1}}{{S}_{0}}]}}}({{t}_{1}},{{t}_{2}},{{\lambda }_{q}}), \\ \end{gathered} $$
(5)
$$\begin{gathered} \overline {|M(R + R \to {{{\left. {\mathcal{H}{{[}^{3}}S_{1}^{{(8)}}]} \right|}}^{2}})} \\ = \frac{1}{2}{{\pi }^{2}}\alpha _{s}^{2}\frac{{\left\langle {{{\mathcal{O}}^{\mathcal{H}}}{{[}^{3}}S_{1}^{{(8)}}]} \right\rangle }}{{{{M}^{3}}}}{{F}^{{{{[}^{3}}{{S}_{1}}]}}}({{t}_{1}},{{t}_{2}},{{\lambda }_{q}}), \\ \end{gathered} $$
(6)
$${{F}^{{{{[}^{1}}{{S}_{0}}]}}}({{t}_{1}},{{t}_{2}},{{\lambda }_{q}}) = \frac{{2{{M}^{2}}\lambda _{q}^{2}\sin {{{(\phi )}}^{2}}}}{{{{{({{M}^{2}} + {{t}_{1}} + {{t}_{2}})}}^{2}}}},$$
$$\begin{gathered} {{F}^{{{{[}^{3}}{{S}_{1}}]}}}({{t}_{1}},{{t}_{2}},{{\lambda }_{q}}) \\ = \frac{{{{\lambda }_{q}}[{{{({{t}_{1}} + {{t}_{2}})}}^{2}} + {{M}^{2}}({{t}_{1}} + {{t}_{2}} - 2\sqrt {{{t}_{1}}{{t}_{2}}} \cos (\phi ))]}}{{{{{({{M}^{2}} + {{t}_{1}} + {{t}_{2}})}}^{2}}}}, \\ \end{gathered} $$

where R denotes the Reggeized gluon, \({{\lambda }_{q}} = {{x}_{1}}{{x}_{2}}S = \) \({{M}^{2}} + {{t}_{1}} + {{t}_{2}} + 2\sqrt {{{t}_{1}}{{t}_{2}}} \cos (\phi )\), ϕ is the angle between the initial transverse momenta.

CEM is another widely used model for the hadronization of a \(c\bar {c}\) pair into charmonium. Its improved version (ICEM) is presented in [13]. The \({{\eta }_{{\text{c}}}}\) meson production cross section is related to the production cross section of a \(c\bar {c}\) pair in the ICSM as follows:

$$\begin{gathered} \sigma (p + p \to {{\eta }_{c}} + X) \\ = {{\mathcal{F}}^{{{{\eta }_{{\text{c}}}}}}}\int\limits_M^{2{{m}_{D}}} {\frac{{d\sigma (p + p \to c + \bar {c} + X)}}{{d{{M}_{{c\bar {c}}}}}}} d{{M}_{{c\bar {c}}}}, \\ \end{gathered} $$
(7)

where \({{M}_{{c\bar {c}}}}\) is the invariant mass of the \(c\bar {c}\) pair with 4‑momentum \(p_{{c\bar {c}}}^{\mu } = p_{c}^{\mu } + p_{{\bar {c}}}^{\mu }\), \({{m}_{D}}\) is the mass of the lightest \(D\) meson. To evaluate the kinematic effect associated with the difference in masses of the intermediate state and the final charmonium, the 4‑momenta of a \(c\bar {c}\) pair and the \({{\eta }_{{\text{c}}}}\) meson are related by the relation \({{p}^{\mu }} = ({M \mathord{\left/ {\vphantom {M {{{M}_{{c\bar {c}}}}}}} \right. \kern-0em} {{{M}_{{c\bar {c}}}}}})p_{{c\bar {c}}}^{\mu }\). The universal parameter \({{\mathcal{F}}^{{{{\eta }_{{\text{c}}}}}}}\) is considered as the probability of transformation of the \(c\bar {c}\) pair with invariant mass \(M < {{M}_{{c\bar {c}}}} < 2{{m}_{D}}\) into a \({{\eta }_{{\text{c}}}}\) meson.

In [14], the parameter \(\mathcal{F}\) was found for inclusive production of the \({J \mathord{\left/ {\vphantom {J \psi }} \right. \kern-0em} \psi }\) mesons at LHC energies. In our calculations, we use \({{\mathcal{F}}^{{{{\eta }_{{\text{c}}}}}}}\) = \({{\mathcal{F}}^{{J/\psi }}}\) = 0.02.

The amplitude of production of the process \(R + R \to c + \bar {c}\) within PRA ICEM was obtained in [15].

3 RESULTS AND CONCLUSIONS

In numerical calculations, the factorization scale was chosen to be \(\mu = \xi {{M}_{{\text{T}}}}\), where the transverse final state mass is \(M_{{\text{T}}}^{2} = {{M}^{2}} + p_{{\text{T}}}^{2}\), and \(\xi \) varies from 1/2 to 2 relative to its standard value 1, in order to estimate the theoretical uncertainty due to the freedom of choice of the scale, which is shown in the figures by the filled bars.

Differential cross sections for \({{\eta }_{{\text{c}}}}\) meson production in PRA were calculated within the framework of the CSM, NQCD, and ICEM hadronization models. Among all the octet contributions of the NQCD series, the largest is the contribution of the state \(^{3}S_{1}^{{(8)}}\). The calculation with the \(^{1}S_{0}^{{(8)}}\) contribution results in an extremely small cross section compared to the \(^{1}S_{0}^{{(1)}}\) contribution in the cross section and is not shown in the corresponding figures.

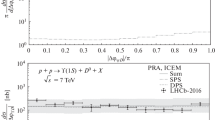
Figure 1 and Fig. 2 compare the experimental data obtained by the LHCb collaboration at an energy \(\sqrt s = \) 7 and 8 TeV with the numerical results obtained in SCM and NQCD, as well as within ICEM. Calculations for the kinematic conditions of the LHCb collaboration were performed for the rapidity range 2.5 < y < 4.5. Figures 3 and 4 show numerical predictions for LHCb and ATLAS at \(\sqrt s = \) 13 TeV. For calculations under the kinematic conditions of ATLAS collaboration, the central rapidity range |y| < 2.5 was chosen.

Fig. 1.
figure 1

Comparison with LHCb data at an energy of 7 TeV within the framework of the NRQCD and ICEM approaches, \(2.5 < y < 4.5\). The dots show the LHCb experimental results with the corresponding errors, the dashed histogram corresponds to the contribution of the singlet state \(^{1}S_{0}^{{(1)}}\), the dash-dotted histogram corresponds to the contribution of the octet state \(^{3}S_{1}^{{(8)}}\), the dash-dotted histogram with two dots corresponds to ICEM calculations.

Full size image
Fig. 2.
figure 2

Comparison with LHCb data at an energy of 8 TeV within the framework of the NRQCD and ICEM approaches, \(2.5 < y < 4.5\). Histogram designations are same as in Fig. 1.

Full size image
Fig. 3.
figure 3

Predictions for LHCb at an energy of 13 TeV, \(2.5 < y < 4.5\). Histogram designations are same as in Fig. 1.

Full size image
Fig. 4.
figure 4

Predictions for ATLAS at an energy of 13 ТeV, \(\left| y \right| < 2.5\). Histogram designations are same as in Fig. 1.

Full size image

PRA calculations in the leading approximation of perturbation theory are consistent with the LHCb experimental data within the limits of the uncertainty of theoretical calculations and experimental errors. As can be seen from Figs. 1 and 2, the contribution of the state to the \(^{3}S_{1}^{{(8)}}\) production cross section of \({{\eta }_{c}}\) turns out to be comparable to the contribution of the \(^{1}S_{0}^{{(1)}}\) singlet, which is sufficient to describe the LHCb data. Thus, calculations in PRA for SCM and NQCD models confirm the conclusion obtained in calculations in the next-to-leading approximation in the strong coupling constant within the framework of the collinear parton model in [16]. The curves corresponding to PRA ICEM lie below those for SCM for \({{\mathcal{F}}_{{{{\eta }_{{\text{c}}}}}}} = {{\mathcal{F}}_{{J/\psi }}}\), but are consistent with the data within the uncertainty of theoretical calculations and experimental errors. This may point to the fact that the choice of the hadron factor \({{\mathcal{F}}_{{{{\eta }_{{\text{c}}}}}}} = {{\mathcal{F}}_{{J/\psi }}}\) is not sufficiently justified.