Study of the Production of Positively Charged Pions in Proton–Proton Collisions in the Range of Primary Momenta between 1345 and 1536 MeV/$c$

Abstract

Differential cross sections obtained for the reaction $pp\to pn\pi^{+}$ at five incident proton momenta of 1345, 1393, 1439, 1486, and 1536 MeV/c are presented. The respective measurements were performed with the aid of a hydrogen-filled bubble chamber. The angular and mass distributions in two-particle channels are compared with the predictions of the one-pion-exchange model and are subjected to a partial-wave analysis with the aim of determining the contributions of various partial waves to the process of pion production in the energy region being studied.

1 INTRODUCTION

Nucleon–nucleon interaction is one of the important processes in hadron physics. Single pion production in nucleon–nucleon collisions is a dominant inelastic process at energies around 1 GeV. Its study, both experimental and theoretical, is aimed at establishing the connection between hadron physics and quantum chromodynamics as a fundamental theory. Although many experiments have already been performed at similar energies [1–8], there still remains the problem of estimating the contribution of isoscalar ($T=0$) partial waves in inelastic neutron–proton collisions. In order to determine the isoscalar contribution, it is necessary to know the isovector part, which can be found quite reliably from data on pion production in proton–proton ($pp$) collisions. The present article reports on the ultimate stage in the series of studies devoted to an analysis of data measured at the synchrocyclotron of Petersburg Nuclear Physics Institute (PNPI, Gatchina) [1–3]. We supplemented the data obtained in those studies and in [4] with data on the reaction $pp\to pn\pi^{+}$ that were obtained at five values of the incident proton momentum in the range of kinetic energies below 1 GeV. In the same way as in the earlier studies, we compare these data with the predictions of the one-pion-exchange (OPE) model and perform a partial-wave analysis in order to determine the contributions of various partial waves.

2 EXPERIMENT AND SELECTION OF DATA

The experiment discussed here was performed at the PNPI synchrocyclotron by employing a 35-cm bubble chamber placed in a magnetic field of strength 14.8 kG. The energy of 1 GeV primary extracted proton beam was reduced by means of a copper absorber of appropriate thickness. Following the absorber, the proton beam was formed by three bending magnets and eight quadrupole lenses. The momentum value was set on the basis of the currents in the bending magnets according to the calibration with the aid of a current-carrying filament. In addition, the primary momentum was tested by measuring the curvature of tracks and by analyzing the subsequent kinematics of events of elastic $pp$ scattering. The momentum of protons incident to the chamber was determined with an error of $\pm$2 MeV/$c$. The root-mean-square spread of the beam momentum was 4 to 5${\%}$. The admixture of heavier particles ($d$, $t$, and He) in the beam was determined by the time of flight and was found to be negligible.

In all, about 200000 stereo photographs were obtained. On average, the irradiation density was 12 to 15 tracks per photograph. Since the experiment was initially aimed at studying the neutral pion production process, events in which tracks in the photograph plane were directed into the forward area with a scattering angle smaller than 60${}^{0}$ (kinematics of events of the reaction $pp\to pp\pi^{0}$) were selected in scanning the photographs. The double-scan efficiency was 99${\%}$. The selected events could belong to the following reactions:

$$pp\to pp,$$

(1)

$$pp\to pn\pi^{+},$$

(2)

$$pp\to pp\pi^{0},$$

(3)

$$pp\to pn\pi^{+}\pi^{0},$$

(4)

$$pp\to d\pi^{+},$$

(5)

$$pp\to d\pi^{+}\pi^{0}.$$

(6)

All events that fall within the useful volume of the chamber and which are appropriate for measurement were handled by means of a semiautomated measuring device (PUOS, which is the acronym of the Russian name) [9]. The identification of the reaction channels was based on employing $\chi^{2}$ values for each specific event at a 1${\%}$ confidence level. If the $\chi^{2}$ values for two hypotheses fell within the fiducial interval, a visual ionization (estimation of the track-ionization density and comparison of the result with the measured momentum of the tracking particle) was invoked in order to identify a positive particle. This made it possible to arrive at a definitive conclusion on the physics hypothesis for the event being considered. Table 1 gives the momenta of protons incident to the chamber and the number of events of the reaction $pp\to pn\pi^{+}$ at each momentum value.

Table 1 Momenta of incident protons and numbers of events of the reaction $pp\to pn\pi^{+}$ at each momentum

3 RESULTS AND THEIR COMPARISON WITH THE PREDICTIONS OF THE OPE MODEL

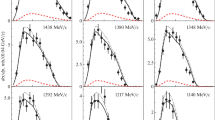
For five values of the incident proton momentum, Figs. 1–5 show the experimental distributions of the momentum transfer to final particles and the angles of final particles in the reaction $pp\to pn\pi^{+}$ in the center-of-mass (c.m.) frame, as well as mass and momentum spectra in the c.m. frame. It is noteworthy that, in contrast to a symmetric distribution at higher energies [1, 2], the angular distribution of pions exhibits a deficit of pions in the backward hemisphere because of the selection of events where the tracks are directed into the forward hemisphere. The experimental data are presented along with results of the calculation based on the OPE model [10–12] (dashed curves) where pole diagrams involving the exchange of $\pi^{+}$ and $\pi^{0}$ mesons are taken into account. The dotted curves represent distributions determined by the phase space. The momentum-transfer distributions are peculiar to one-meson exchange, and this justifies the comparison of our data with the respective model. The calculations on the basis of the OPE model are normalized to the experimental data. One can see that the OPE model describes well the momentum-transfer distributions and is applicable to all of the other distributions. It should be noted that, within this model, the intermediate state of the $\pi N$-scattering amplitude is restricted to the $P_{33}$ wave under the assumption of a leading role of the $\Delta_{33}$ resonance. The data in the figures show that, nevertheless, the OPE model describes the experimental data fairly well.

Fig. 1

Distribution of the momentum transfer from the target to final nucleons (proton and neutron) and from the incident proton to the pion for events of the reaction $pp\to$ $pn\pi^{+}$ in the laboratory frame (first row of panels), angular distribution of particles in the center-of-mass frame (second row of panels), effective-mass distribution (third row of panels), and distribution of particle momenta in the c.m. frame at the incident proton momentum of 1536 MeV/$c$ (fourth row of panels). The rows of panels are reckoned from top to bottom. The crosses on display stand for experimental data. The dashed and dotted curves represent the results of, respectively, calculations based on the OPE model and phase-space calculations.

Fig. 2

Analogous distributions for the incident proton momentum of 1486 MeV/$c$. The crosses stand for experimental data. The notation for the curve is identical to that in Fig. 1.

Fig. 3

Analogous distributions for the incident proton momentum of 1439 MeV/$c$. The crosses stand for experimental data. The notation for the curves is identical to that in Fig. 1.

Fig. 4

Analogous distributions for the incident proton momentum of 1393 MeV/$c$. The crosses stand for experimental data. The notation for the curves is identical to that in Fig. 1.

Fig. 5

Analogous distributions for the incident proton momentum of 1345 MeV/$c$. The crosses stand for experimental data. The notation for the curves is identical to that in Fig. 1.

4 FORMALISM OF PARTIAL-WAVE ANALYSIS AND ITS RESULTS

A partial-wave analysis of these data was performed within the formalism that was described in detail in [13–15]. This is the fully covariant formalism based on the expansion of the total scattering amplitude in terms of partial-wave amplitudes having fixed spin–orbit characteristics of initial, intermediate, and final states. Therefore, it is natural to use the spectroscopic notation ${}^{2S+1}L_{J}$ for two-body partial waves of intrinsic spin $S$, orbital angular momentum $L$, and total spin $J$.

The total amplitude can be represented as the sum of partial-wave amplitudes [13]; that is,

$$A=\sum\limits_{\alpha}A_{\textrm{tr}}^{\alpha}\left(s\right)Q_{\mu_{1}\ldots\mu_{J}}^{\textrm{in}}\left({SLJ}\right)$$

(7)

$${}\times A_{2\textrm{body}}^{S_{2},L_{2},J_{2}}\left({s_{i}}\right)Q_{\mu_{1}\ldots\mu_{J}}^{\textrm{fin}}\left({i,S_{2}L_{2}J_{2}S^{\prime}L^{\prime}J}\right),$$

where $Q$ are operators of the spin–orbital expansion of initial and final states [14], $A_{\textrm{tr}}^{\alpha}$ is the transition amplitude, and $A_{2\textrm{body}}^{S_{2},L_{2},J_{2}}$ describes the rescattering process in the final two-body channel. The energy dependence of partial-wave amplitudes between initial and final states is taken in the form

$$A_{\textrm{tr}}^{\alpha}\left(s\right)=\frac{a_{1}^{\alpha}+a_{3}^{\alpha}\sqrt{s}}{s-a_{4}^{\alpha}}e^{ia_{2}^{\alpha}},$$

(8)

where the superscript $\alpha$ includes all quantum numbers of the respective partial wave, $s$ is the square of the invariant energy of the initial nucleon–nucleon system, and $a_{i}^{\alpha}$ are real-valued parameters. The parameters $a_{4}^{\alpha}$ determine the pole singularities lying in the region of left-hand singularities of partial-wave amplitudes, and $a_{2}^{\alpha}$ introduces phases determined by the rescattering of three final particles. In order to suppress the contributions of amplitudes at high relative momenta, we introduced the Blatt–Weisskopf form factors. Thus, the energy-dependent part of partial-wave amplitudes involving the creation of a resonance, for example, in a two-particle system 12 (say, $\pi p$) and a spectator particle 3 ($n$) has the form

$$A^{\prime}=\frac{A_{\textrm{tr}}^{\alpha}A_{2\textrm{body}}^{S_{2},L_{2},J_{2}}(s_{12})q^{L}k_{3}^{L^{\prime}}}{\sqrt{F\left({q^{2},L,R}\right)F(k_{3}^{2},L^{\prime},r_{3})}},$$

(9)

where $q$ is the incident proton momentum and $k_{3}$ is the spectator particle momentum, both of these momenta being calculated in the reaction c.m. frame. The exact expression for the Blatt–Weisskopf form factor $F(k^{2},L,R)$ can be found, for example, in [14]. One could expect a value between 1 and 4 fm for the effective range $R$ of the initial proton–proton system. However, this value can hardly be determined to a high precision in the present analysis because of a relatively large distance from the $pp$ threshold. In fact, we do not observe any sensitivity to variations in this parameter and fix it at 1.2 fm. A very close result was observed for $r_{3}$. For our ultimate fits, we therefore fixed this parameter at 1.2 fm as well.

In order to describe the energy dependence in the $\pi N$ system we introduced two resonances: $\Delta$(1232)$\dfrac{3^{+}}{2}$ and the Roper resonance $N$(1440)$\dfrac{1^{+}}{2}$. The respective resonance contributions are parametrized in terms of relativistic Breit–Wigner amplitudes in the form

$$A_{2\textrm{body}}^{S_{2},L_{2},J_{2}}\left({s_{12}}\right)=\frac{k_{12}^{L_{2}}}{\sqrt{F\left({k_{12}^{2},L_{2},r_{12}}\right)}}$$

(10)

$${}\times\frac{1}{M_{R}^{2}-s_{12}-iM_{R}\Gamma},$$

$$\Gamma=\Gamma_{R}\frac{M_{R}k_{12}^{2L_{2}+1}F(k_{R}^{2},L_{2},r_{12})}{\sqrt{s_{12}}k_{R}^{2L_{2}+1}F(k_{12}^{2},L_{2},r_{12})},$$

where $s_{12}$ is the square of the invariant energy in the 12 channel, $k_{12}$ is the relative momentum of particles 1 and 2 in their rest frame, and $r_{12}$ is the effective range. The relative momentum in resonance decay, $k_{R}$, is calculated at the resonance mass $M_{R}$. For $\Delta$(1232), we use the PDG (Particle Data Group) values of $M_{R}$ and $\Gamma_{R}$ from [16] with $r_{12}=0.8$ fm. The Roper state was parametrized by employing the coupling constants found in the analysis that was performed in [14], where the decays of this state to $\pi N$, $\Delta\pi$, and $N(\pi\pi)_{S\mathrm{-wave}}$ were determined.

In order to describe the final nucleon–nucleon interaction, we used the parametrization

$$A_{2\textrm{body}}^{S_{2},L_{2},J_{2}}\left({s_{23}}\right)$$

(11)

$${}=\frac{\sqrt{s_{23}}}{1-\frac{1}{2}r_{23}^{\beta}k_{23}^{2}a^{\beta}+ik_{23}a^{\beta}\frac{k_{23}^{2L_{2}}}{F(k_{23},r_{23}^{\beta},L_{2})}}.$$

For $s$ waves, this expression coincides with that based on the scattering-length approximation and proposed in [17, 18]. Thus, we can treat the parameter $a^{\beta}$ as the nucleon–nucleon scattering length and $r^{\beta}$ as the effective range for the nucleon–nucleon system. For $S$ waves, we fixed at $a(^{1}S_{0})={-}23.7$ fm and $a(^{3}S_{1})=5.3$ fm the $pn$ scattering lengths and at $r(^{1}S_{0})=2.8$ fm and $r(^{3}S_{1})=1.8$ fm the respective effective ranges.

A simultaneous fit to the data discussed here and data that correspond to the higher momenta of 1581, 1628, and 1683 MeV/$c$ and which take into account the production of $\pi^{0}$ [1–3] and $\pi^{+}$ [4] mesons made it possible to determine more precisely the contributions of partial waves characterized by higher orbital angular momenta of $L\geqslant 3$. In the analysis of low-energy data alone, the contribution of these partial waves led to an unstable solution—in particular, to a violation of convergence of the procedure for optimizing parameter values and, hence, to large statistical errors in determining the contributions of partial-wave amplitudes. In the simultaneous fit, the statistical errors calculated in a standard way on the basis of correlation of the errors in the code for minimizing parameters turned out to be substantially smaller than the systematic errors associated with the introduction (or suppression) of partial waves that contributed less than 1${\%}$. Figure 6 shows the resulting fit to the data measured at the initial proton momentum of 1486 MeV/$c$. Our partial-wave analysis (histograms) describes satisfactorily the experimental data. Qualitatively, the descriptions of the data at the different values of the incident proton momentum are very close to the description of the data in Fig. 6. A determination of the contributions of various partial-wave amplitudes to the cross section for single pion production was one of the main objectives of the present partial-wave analysis. The contributions of isovector amplitudes to the reaction $pp\to pn\pi^{+}$ are shown in Fig. 7 versus the beam momentum. We have already mentioned that the errors are primarily systematic and stem from the poorly controllable contribution of small partial-wave amplitudes.

Fig. 6

Results of a partial-wave analysis within the even-by-event likelihood method along with some experimental distributions at the beam momentum 1486 MeV/$c$: (first row of panels) angular distributions of particles in the c.m. frame; (second row of panels) mass distributions; and (third and fourth rows of panels) angular distributions of particles in, respectively, the helicity frame and the Gottfried–Jackson frame. The points with error bars on display stand for experimental data, while the histograms represent the results of our partial-wave analysis. The value at the top of each panel is that of $\chi^{2}$ per degree of freedom for the description of the respective distribution in terms of the solution obtained from the partial-wave analysis of the data.

Fig. 7

Contributions (in percent) of the most important isovector waves to the reaction $pp\to pn\pi^{+}$.

5 CONCLUSIONS

New experimental data on the production of positively charged pions in $pp$ collisions have been compared with the results of the calculations based on the OPE model. The results of the calculations agree qualitatively with the experimental data at all momenta of incident protons. The partial-wave analysis performed in the present article made it possible to determine the contributions of dominant partial waves to the pion-production process in the range of energies below 1 GeV.