1 INTRODUCTION

In 1950, Fermi [1, 2] conjectured that in collisions of high-energy particles, the number of formed new particles is so large that their mean free paths are much smaller than the size of the generated nuclear (hadron) matter cloud. As a result, thermal equilibrium sets in soon in this cloud, and, for example, the energy distribution of particles escaping from the cloud can be described using relations of statistical mechanics. Later, Pomeranchuk [3] paid attention to the fact that the matter formed in this case expands at relativistic velocities, and final particles are formed when the temperature at a given point becomes on the order of their mass. Landau [4] noted that the nuclear matter cloud emerging during collisions of ultrarelativistic particles initially has the shape of a thin disk due to the Lorentz contraction; for this reason, the initial stage of the flow is predominantly one-dimensional. If we denote the initial thickness of the disk as 2l and direct the x axis along the normal to the disk, the equations of relativistic fluid dynamics are simplified under the assumption of ultrarelativistic velocities \({v}\) of the flow (c – \({v}\) ≪ c, c being the velocity of light). Landau obtained the asymptotic solutions to these equations for ln(t/l) ≫ 1, ln[(ct – x)/l] ≫ 1 with logarithmic accuracy, which enabled him to estimate the main parameters of the flow. Subsequently, the Landau theory has formed the basis for the theory of multiple production of particles during collisions of elementary particles and atomic nuclei accelerated to ultrarelativistic velocities and has been generally confirmed experimentally (see, for example, [5, 6]).

The exact solution for the 1D stage of the flow was obtained by Khalatnikov [7]. The formulation of the problem considered by him can be described as follows. Let us suppose that a nuclear matter at the initial instant occupies a layer in spatial region –l ≤ x ≤ l and has temperature T0 ≫ mc2, where m is the characteristic mass of hadrons (say, pions) forming the matter. At such ultrarelativistic temperatures, it is natural to assume that the following equation of state holds:

$$p = \varepsilon {\text{/}}3,$$
((1))

where p is the pressure and ε is the energy density. This equation of state corresponds to velocity of sound [8]

$${{c}_{s}} = c\sqrt {\frac{{\partial p}}{{\partial \varepsilon }}} = \frac{c}{{\sqrt 3 }},$$
((2))

which is independent of the parameters of the medium. At the very initial stage of expansion of the layer, self-similar rarefaction waves centered at points x = ±l start propagating from its edges towards one another. At instant tc = l/cs = \(\sqrt 3 \)l/c, these waves collide at the center of matter distribution at point x = 0, leading to the formation between them of the region of general solution to the relativistic fluid dynamics equation, which borders the expansion waves at its edges. Therefore, the general solution must satisfy the boundary conditions following from the requirement of its “matching” with rarefaction waves. Khalatnikov proved [7] an important theorem according to which a 2D relativistic flow is always a potential flow and reduced the equation for the potential to a second-order linear differential equation with constant coefficients with the help of the hodograph transformation. This equation, which is often referred to as the Khalatnikov equation in the context of relativistic fluid dynamics, is analytically equivalent to the telegraph equation that is usually solved with the help of the Laplace transformation in the case of problems with initial conditions [9]. Khalatnikov skillfully employed this method, obtained the exact solution that satisfied the required boundary conditions, and demonstrated that this solution reproduces the Landau asymptotic solution in the corresponding limit (see also [10]). More detailed analysis of the Khalatnikov solution was performed in a number of subsequent publications [11–13].

Despite the elegance of the Khalatnikov solution, it was obtained in the form in which the symmetry of the flow relative to reflection in plane x = 0 is not observed explicitly, which complicates its analysis in certain respects. In addition [7], the operational calculus method for solving the Khalatnikov equation is apparently applicable only to systems with a constant velocity of sound and cannot be generalized to other problems in the case when the equation for the potential of the flow on the hodograph plane, which generally belongs to the class of the Euler–Poisson equations, has constant coefficients. For this reason, we will solve here the Landau–Khalatnikov problem using an alternative Riemann method [14–16] that is applicable to a wider class of the equations of state of the matter. In particular, this method was employed in the recent study [17] for solving the problem of expansion of the Bose–Einstein condensate upon the elimination of a trap with a rectangular potential in the form of a “box.” The form of the solution to the Landau–Khalatnikov problem obtained in this study reflects the flow symmetry explicitly. This solution is used for obtaining the speed distribution of formed particles and the exact relations describing the temperature at the distribution center and the trajectories of the boundaries of the expanding cloud of matter. These forms of the solution are compared, and their equivalence is proved.

2 RELATIVISTIC FLUID DYNAMICS

Beginning from this section, we will use, for simplifying notation, the system of units in which velocity of light c and initial temperature T0 in the layer equal unity. We will briefly describe the main concepts of relativistic fluid dynamics to introduce the required definitions and relations of the theory.

2.1 Basic Equations

It is well known [8, 18] that the relativistic fluid dynamics equations are contained in the conservation laws for a relativistic flow, which have the following form in the case of a 1D flow:

$$\frac{{\partial {{T}^{{00}}}}}{{\partial t}} + \frac{{\partial {{T}^{{01}}}}}{{\partial x}} = 0,\quad \frac{{\partial {{T}^{{01}}}}}{{\partial t}} + \frac{{\partial {{T}^{{11}}}}}{{\partial x}} = 0,$$
((3))

where energy–momentum tensor components Tik are given by

$$\begin{gathered} {{T}^{{00}}} = (\varepsilon + p){{u}^{0}}{{u}^{0}} - p,\quad {{T}^{{01}}} = (\varepsilon + p){{u}^{0}}{{u}^{1}}, \\ {{T}^{{11}}} = (\varepsilon + p){{u}^{1}}{{u}^{1}} + p, \\ \end{gathered} $$
((4))

ui is the 4-velocity vector,

$$({{u}^{0}},{{u}^{1}}) = \left( {\frac{1}{{\sqrt {1 - {{{v}}^{2}}} }},\frac{{v}}{{\sqrt {1 - {{{v}}^{2}}} }}} \right) = (\cosh u,\sinh y),$$
((5))

and we have introduced rapidity y associated with flow velocity \({v}\) by relation \({v}\) = tanhy so that the Lorentz transformation is reduced to a hyperbolic rotation through “angle” y. Substituting expressions (5) into (4) and considering sound velocity definition \(c_{s}^{2}\) = ∂p/∂ε, we arrive at system of equations

$$\begin{gathered} ({{\cosh }^{2}}y + c_{s}^{2}{{\sinh }^{2}}y)\frac{{\partial \varepsilon }}{{\partial t}} \\ \, + 2(\varepsilon + p)\sinh y\cosh y\frac{{\partial y}}{{\partial t}} \\ \, + (1 + c_{s}^{2})\sinh y\cosh y\frac{{\partial \varepsilon }}{{\partial x}} \\ \, + (\varepsilon + p)({{\sinh }^{2}}y + {{\cosh }^{2}}y)\frac{{\partial y}}{{\partial x}} = 0, \\ \end{gathered} $$
$$\begin{gathered} (1 + c_{s}^{2})\sinh y\cosh y\frac{{\partial \varepsilon }}{{\partial t}} \\ \, + (\varepsilon + p)({{\sinh }^{2}}y + {{\cosh }^{2}}y)\frac{{\partial y}}{{\partial t}} \\ \, + ({{\sinh }^{2}}y + c_{s}^{2}{{\cosh }^{2}}y)\frac{{\partial \varepsilon }}{{\partial x}} \\ \, + 2(\varepsilon + p)\sinh y\cosh y\frac{{\partial y}}{{\partial x}} = 0. \\ \end{gathered} $$

Characteristic velocities of this system of first-order differential equations,

$${{{v}}_{ \pm }} = \frac{{{v} \pm {{c}_{s}}}}{{1 \pm {v}{{c}_{s}}}},$$
((6))

have the explicit physical meaning: the velocity of signal propagation is the sum of the flow velocity and the velocity of sound in accordance with the relativistic law of velocity summation; the sound can propagate along the flow and against it. We can easily find the Riemann invariants corresponding to these velocities [8, 18, 19]:

$${{r}_{ \pm }} = y \pm \int\limits_0^\varepsilon {\frac{{{{c}_{s}}d\varepsilon }}{{\varepsilon + p}},} $$
((7))

in the case of ultrarelativistic equation of state (1), this gives

$${{r}_{ \pm }} = y \pm \sqrt 3 \theta ,$$
((8))

where we have introduced variable θ = lnT instead of temperature and have taken into account the fact that equation of state (1) gives the following expression for energy density:

$$\varepsilon = {{T}^{4}}.$$
((9))

The velocity of the flow and the temperature of the fluid as functions of the Riemann invariants have form

$$\begin{gathered} {v} = \tanh y = \tanh \left( {\frac{{{{r}_{ + }} + {{r}_{ - }}}}{2}} \right), \\ T = {{e}^{\theta }} = \exp \left( {\frac{{{{r}_{ + }} - {{r}_{ - }}}}{{2\sqrt 3 }}} \right). \\ \end{gathered} $$
((10))

The hydrodynamic equations written in terms of Riemann invariants acquire a simple diagonal form:

$$\frac{{\partial {{r}_{ \pm }}}}{{\partial t}} + {{{v}}_{ \pm }}({{r}_{ + }},{{r}_{ - }})\frac{{\partial {{r}_{ \pm }}}}{{\partial x}} = 0,$$
((11))

where characteristic velocities

$${{{v}}_{ \pm }} = \frac{{\tanh [({{r}_{ + }} + {{r}_{ - }}){\text{/}}2] \pm 1{\text{/}}\sqrt 3 }}{{1 + \tanh [({{r}_{ + }} + {{r}_{ - }}){\text{/}}2]{\text{/}}\sqrt 3 }}$$
((12))

can also be easily expresses in terms of the Riemann invariants.

2.2 Rarefaction Waves

Equations (11) and (12) immediately give the solutions for rarefaction waves. Let us consider, for example, the right edge of the initial distribution, located at x = l. Since the matter is at rest in the initial state, and the temperature equals unity everywhere, both Riemann invariants in the initial state equal zero. Up to the instant of collision tc = \(\sqrt 3 \)l, the right rarefaction wave evolves independently of the left wave, and parameter l appears in the corresponding solution in the form of combination x – l. Therefore, the Riemann invariants in it can depend only on self-similar variable (x – l)/t. Then relation (11) immediately implies that one of the Riemann invariants must be constant, and variable (x – l)/t must equal the characteristic velocity corresponding to the other Riemann invariant. The flow velocity in the right rarefaction wave is positive (i.e., y > 0), and the temperature decreases upon the expansion of the matter (i.e., θ < 0). Consequently, in the right rarefaction wave, the Riemann invariant

$${{r}_{ + }} = y + \sqrt 3 \theta = 0$$
((13))

must remain unchanged. Using relation

$$\frac{{x - l}}{t} = {{{v}}_{ - }} = \frac{{{v} - 1{\text{/}}\sqrt 3 }}{{1 - {v}{\text{/}}\sqrt 3 }}$$
((14))

we then obtain the flow velocity distribution

$${v} = \frac{{\sqrt 3 (x - l){\text{/}}t + 1}}{{\sqrt 3 + (x - l){\text{/}}t}},$$
((15))

while from relations (9), (10), and (13), we get energy density distribution

$$\varepsilon = {{\left( {\frac{{1 - 1{\text{/}}\sqrt 3 }}{{1 + 1{\text{/}}\sqrt 3 }} \times \frac{{1 - (x - l){\text{/}}t}}{{1 + (x - l){\text{/}}t}}} \right)}^{{2/\sqrt 3 }}}.$$
((16))

The boundary with vacuum, at which ε → 0, moves to the right at the velocity of light, which is not surprising since the medium consists of particles with thermal velocities equal to the velocity of light in our approximation. The wave propagates to the bulk of the stationary medium, at the boundary with which ε = 1, with the velocity of sound (x – l)/t = –1/\(\sqrt 3 \). An analogous solution for the left rarefaction wave depending on self-similar variable (x + l)/t can be constructed in exactly the same way. Riemann invariant r– = y – \(\sqrt 3 \)θ is constant along this wave, which corresponds to a negative flow velocity with y < 0.

2.3 Khalatnikov Equation

After the collision of rarefaction waves at instant tc = \(\sqrt 3 \)l at x = 0, the region of the general solution is formed between them, along which both Riemann invariants r± change with x and t, and obtaining of this solution is a more complicated problem.

Khalatnikov proved [7] that conservation laws (3) lead to equation

$$\frac{{\partial (T{{u}^{1}})}}{{\partial t}} - \frac{{\partial (T{{u}^{0}})}}{{\partial x}} = 0,$$
((17))

indicating that we can introduce potential ϕ = ϕ(x, t) such that

$$d\phi = T\cosh y \cdot dt - T\sinh y \cdot dx.$$

Introducing additionally variables x± = t ± x of the light cone and passing from T and y to Riemann invariants r± as dependent variables, we can write this differential in form

$$d\phi = A({{r}_{ + }},{{r}_{ - }})d{{x}_{ - }} + B({{r}_{ + }},{{r}_{ - }})d{{x}_{ + }},$$
((18))

where

$$\begin{gathered} A({{r}_{ + }},{{r}_{ - }}) = \frac{1}{2}{{e}^{{\theta + y}}} \\ = \frac{1}{2}\exp \left[ {\frac{1}{2}\left( {1 + \frac{1}{{\sqrt 3 }}} \right){{r}_{ + }} + \frac{1}{2}\left( {1 - \frac{1}{{\sqrt 3 }}} \right){{r}_{ - }}} \right], \\ B({{r}_{ + }},{{r}_{ - }}) = \frac{1}{2}{{e}^{{\theta - y}}} \\ = \frac{1}{2}\exp \left[ { - \frac{1}{2}\left( {1 - \frac{1}{{\sqrt 3 }}} \right){{r}_{ + }} - \frac{1}{2}\left( {1 + \frac{1}{{\sqrt 3 }}} \right){{r}_{ - }}} \right]. \\ \end{gathered} $$
((19))

Following Khalatnikov, we perform Legendre transformation

$$W = \phi - A{{x}_{ - }} - B{{x}_{ + }},$$

where variables W, x–, and x+ are treated as functions of the Riemann invariants, which corresponds to the hodograph transformation familiar from gas dynamics [8, 19]. This gives

$$\begin{gathered} dW = \frac{1}{2}\left[ { - \left( {1 + \frac{1}{{\sqrt 3 }}} \right)A{{x}_{ - }} + \left( {1 - \frac{1}{{\sqrt 3 }}} \right)B{{x}_{ + }}} \right]d{{r}_{ + }} \\ + \frac{1}{2}\left[ { - \left( {1 - \frac{1}{{\sqrt 3 }}} \right)A{{x}_{ - }} + \left( {1 + \frac{1}{{\sqrt 3 }}} \right)B{{x}_{ + }}} \right]d{{r}_{ - }}, \\ \end{gathered} $$

so that

$$\frac{1}{2}\left[ { - \left( {1 + \frac{1}{{\sqrt 3 }}} \right)A{{x}_{ - }} + \left( {1 - \frac{1}{{\sqrt 3 }}} \right)B{{x}_{ + }}} \right] = \frac{{\partial W}}{{\partial {{r}_{ + }}}},$$
$$\frac{1}{2}\left[ { - \left( {1 - \frac{1}{{\sqrt 3 }}} \right)A{{x}_{ - }} + \left( {1 + \frac{1}{{\sqrt 3 }}} \right)B{{x}_{ + }}} \right] = \frac{{\partial W}}{{\partial {{r}_{ - }}}}.$$

Therefore, if function W(r+, r–) has been determined, variables x and t are expressed in terms of the Riemann invariants:

$$\begin{gathered} x = \sqrt 3 {{e}^{{ - \theta }}}\left\{ {\left( {\frac{{\cosh y}}{{\sqrt 3 }} + \sinh y} \right)\frac{{\partial W}}{{\partial {{r}_{ - }}}}} \right. \\ \left. { + \left( {\frac{{\cosh y}}{{\sqrt 3 }} - \sinh y} \right)\frac{{\partial W}}{{\partial {{r}_{ + }}}}} \right\}, \\ t = \sqrt 3 {{e}^{{ - \theta }}}\left\{ {\left( {\frac{{\sinh y}}{{\sqrt 3 }} + \cosh y} \right)\frac{{\partial W}}{{\partial {{r}_{ - }}}}} \right. \\ \left. { + \left( {\frac{{\sinh y}}{{\sqrt 3 }} - \cosh y} \right)\frac{{\partial W}}{{\partial {{r}_{ + }}}}} \right\}, \\ \end{gathered} $$
((20))

which gives the solution to the problem in implicit form.

We have formally solved so far Eq. (17) by introducing potential W = W(r+, r–). To obtain the equation for W, we can use the entropy conservation law as the second equation of relativistic fluid dynamics (we denote the entropy density by σ [8]):

$$\frac{{\partial (\sigma {{u}^{0}})}}{{\partial t}} + \frac{{\partial (\sigma {{u}^{1}})}}{{\partial x}} = 0.$$
((21))

The entropy density for a fluid with the ultrarelativistic equation of state can be expressed in terms of the Riemann invariants:

$$\sigma = \frac{4}{3}{{T}^{3}} = \frac{4}{3}\exp \left[ {\frac{{\sqrt 3 }}{2}({{r}_{ + }} - {{r}_{ - }})} \right].$$
((22))

Multiplying Eq. (21) by Jacobian ∂(x, t)/∂(r+, r–), using expressions (22) and (10), and performing simple transformations, we obtain equation

$$\frac{{{{\partial }^{2}}W}}{{\partial {{r}_{ + }}\partial {{r}_{ - }}}} - \frac{1}{{2\sqrt 3 }}\left( {\frac{{\partial W}}{{\partial {{r}_{ + }}}} - \frac{{\partial W}}{{\partial {{r}_{ - }}}}} \right) = 0.$$
((23))

This equation written in terms of independent variables y and θ instead of r± was derived by Khalatnikov [7]. It is equivalent analytically to the known telegraph equation, for solving which mathematical methods have been thoroughly developed [9, 15, 16]. Some classes of such solutions are used in the theory of multiple production of particles (see, for example, [20, 21]). In the case of the Landau–Khalatnikov problem of expansion of the layer, in which specific boundary conditions play an important role, the Riemann method in which the solution is written directly in terms of the boundary conditions of the problem is apparently quite convenient. This method will be employed in the next section.

3 THE LANDAU–KHALATNIKOV PROBLEM

3.1 Boundary Conditions

Potential W defining the fluid flow by expressions (20) must satisfy Eq. (23) as well as the boundary conditions following from the matching of the general solution at its edge with rarefaction waves. If we solve Eq. (20) for derivatives ∂W/∂r±, the solution can be written after simple transformation in the form

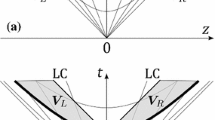
$$\begin{gathered} \frac{{\partial W}}{{\partial {{r}_{ - }}}} = \frac{{{{e}^{\theta }}}}{2}\left( {\cosh y - \frac{{\sinh y}}{{\sqrt 3 }}} \right)\left( {x - \frac{{\tanh y - 1{\text{/}}\sqrt 3 }}{{1 - \tanh y{\text{/}}\sqrt 3 }}t} \right), \\ \frac{{\partial W}}{{\partial {{r}_{ + }}}} = \frac{{{{e}^{\theta }}}}{2}\left( {\cosh y + \frac{{\sinh y}}{{\sqrt 3 }}} \right)\left( {x - \frac{{\tanh y + 1{\text{/}}\sqrt 3 }}{{1 + \tanh y{\text{/}}\sqrt 3 }}t} \right). \\ \end{gathered} $$
((24))

The curves describing the dependences of the Riemann invariants on coordinate x at fixed instant t are shown in Fig. 1. Riemann invariant r+ vanishes at the right boundary of the general solution, while Riemann invariant r– vanishes at the left boundary, where x and t satisfy the solution in the form of rarefaction waves (see relation (14)):

$$\begin{gathered} x - \frac{{\tanh y - 1{\text{/}}\sqrt 3 }}{{1 - \tanh y{\text{/}}\sqrt 3 }}t = l,\quad {{r}_{ + }} = 0, \\ x - \frac{{\tanh y + 1{\text{/}}\sqrt 3 }}{{1 + \tanh y{\text{/}}\sqrt 3 }}t = - l,\quad {{r}_{ - }} = 0. \\ \end{gathered} $$
((25))
Fig. 1.
figure 1

(Color online) Dependences of Riemann invariants r± on coordinate x at a fixed instant t > l\(\sqrt 3 \); xL and xR denote the edges of the general solution, while –l – t and l + t are the boundaries between the left and right rarefaction waves and vacuum.

Full size image

Substituting these expressions into (24), we obtain the boundary conditions in form

$$\begin{gathered} {{\left. {\frac{{\partial W}}{{\partial {{r}_{ - }}}}} \right|}_{{{{r}_{ + }} = 0}}} = \frac{l}{4}\left\{ {\left( {1 - \frac{1}{{\sqrt 3 }}} \right)\exp \left[ {\frac{1}{2}\left( {1 - \frac{1}{{\sqrt 3 }}} \right){{r}_{ - }}} \right]} \right. \\ \left. { + \left( {1 + \frac{1}{{\sqrt 3 }}} \right)\exp \left[ { - \frac{1}{2}\left( {1 + \frac{1}{{\sqrt 3 }}} \right){{r}_{ - }}} \right]} \right\}, \\ {{\left. {\frac{{\partial W}}{{\partial {{r}_{ + }}}}} \right|}_{{{{r}_{ - }} = 0}}} = - \frac{l}{4}\left\{ {\left( {1 + \frac{1}{{\sqrt 3 }}} \right)\exp \left[ {\frac{1}{2}\left( {1 + \frac{1}{{\sqrt 3 }}} \right){{r}_{ + }}} \right]} \right. \\ \left. { + \left( {1 - \frac{1}{{\sqrt 3 }}} \right)\exp \left[ { - \frac{1}{2}\left( {1 - \frac{1}{{\sqrt 3 }}} \right){{r}_{ + }}} \right]} \right\}. \\ \end{gathered} $$
((26))

Since potential W is determined to within an additive constant, we can specify its value W(0, 0) = 0 at the origin of coordinates on hodograph plane (r+, r–). Then integration of Eqs. (26) gives the final form of the boundary conditions on the boundaries between the general and expansion waves:

$$\begin{gathered} W(0,{{r}_{ - }}) = \frac{l}{2}\exp \left( {\frac{{{{r}_{ - }}}}{{2\sqrt 3 }}} \right)\sinh \frac{{{{r}_{ - }}}}{2}, \\ W({{r}_{ + }},0) = - \frac{l}{2}\exp \left( { - \frac{{{{r}_{ + }}}}{{2\sqrt 3 }}} \right)\sinh \frac{{{{r}_{ + }}}}{2}. \\ \end{gathered} $$
((27))

3.2 Riemann Method

Thus, we must solve Eq. (23) with boundary conditions (27) specified on characteristics r+ = 0 and r– = 0. In his fundamental work [14], Riemann proposed the following method for solving this problem. If we are interested in the value of function W at point P = (r+, r–) (Fig. 2), we plot characteristics PA (\(r_{ + }^{'}\) = r+ = const) and PB (\(r_{ - }^{'}\) = r– = const) from point P on hodograph plane (\(r_{ + }^{'}\), \(r_{ - }^{'}\)), which form (with characteristics AO and OB with known values of W(\(r_{ + }^{'}\), 0) and W(0, \(r_{ - }^{'}\)) on them) closed contour \(\mathcal{C}\) = PAOB on this plane. Since quantities (\({{r}_{ + }}\), \({{r}_{ - }}\)) denote the coordinates of the point of “observation” on the hodograph plane, we introduce here notation (\(r_{ + }^{'}\), \(r_{ - }^{'}\)) for running coordinates of points along this contour. We define on this plane vector (V, U) such that integral \(\int_\mathcal{C} ( \)Vd\(r_{ + }^{'}\) + Ud\(r_{ - }^{'}\)) = 0 vanishes, and components of vector (V, U) depends on function W satisfying Eq. (23) as well as on another function R = R(\(r_{ + }^{'}\), \(r_{ - }^{'}\); r+, r–), on which we can impose appropriate conditions without changing the zero value of the above integral. According to Riemann, if we require as such conditions that function R satisfies, first, the conjugate equation, which in our case has form

$$\frac{{{{\partial }^{2}}R}}{{\partial r_{ + }^{'}\partial r_{ - }^{'}}} + \frac{1}{{2\sqrt 3 }}\left( {\frac{{\partial R}}{{\partial r_{ + }^{'}}} - \frac{{\partial R}}{{\partial r_{ - }^{'}}}} \right) = 0,$$
((28))

second, boundary conditions

$$\begin{gathered} \frac{{\partial R}}{{\partial r_{ + }^{'}}} - \frac{R}{{2\sqrt 3 }} = 0\quad {\text{along}}\quad PB, \\ \frac{{\partial R}}{{\partial r_{ - }^{'}}} + \frac{R}{{2\sqrt 3 }} = 0\quad {\text{along}}\quad PA, \\ \end{gathered} $$
((29))

and third, its fixed value at point P,

$$R({{r}_{ + }},{{r}_{ - }};{{r}_{ + }},{{r}_{ - }}) = 1,$$
((30))

the value of W at point P = (r+, r–) is given by

$$\begin{gathered} W(P) = \frac{1}{2}{{(RW)}_{A}} + \frac{1}{2}{{(RW)}_{B}} \\ \, + \int\limits_A^O {Vdr_{ + }^{'} + \int\limits_O^B {Udr_{ - }^{'}} ,} \\ \end{gathered} $$
((31))

where A = (r+, 0), B = (0, r–), O = (0, 0), and U and V can be expressed in terms of boundary values (27) as

$$\begin{gathered} U = \frac{1}{2}\left( {W\frac{{\partial R}}{{\partial r_{ + }^{'}}} - R\frac{{\partial W}}{{\partial r_{ + }^{'}}}} \right) - \frac{{WR}}{{2\sqrt 3 }}, \\ V = \frac{1}{2}\left( {R\frac{{\partial W}}{{\partial r_{ - }^{'}}} - W\frac{{\partial R}}{{\partial r_{ - }^{'}}}} \right) - \frac{{WR}}{{2\sqrt 3 }}. \\ \end{gathered} $$
((32))
Fig. 2.
figure 2

(Color online) Curve describing Riemann invariant r± on hodograph plane (\(r_{ + }^{'}\), \(r_{ - }^{'}\)).

Full size image

Although it seems at first glance that it is not easier to solve Eq. (28) for R than the initial equation for W, boundary conditions (29) are so simple now that function R known as the Riemann function in this theory can be determined easily in our case. Since equation of state (1) is analogous to the nonrelativistic Boyle–Mariotte isothermal equation of state p = \(c_{s}^{2}\)ρ in which isothermal velocity of sound cs is also independent of gas density ρ, Riemann himself [14], who considered such a gas, determined, in fact, the functions required for our analysis. In our case of relativistic fluid dynamics, this function has form

$$\begin{gathered} R(r_{ + }^{'},r_{ - }^{'};{{r}_{ + }},{{r}_{ - }}) = \exp \left[ {\frac{{(r_{ + }^{'} - {{r}_{ + }}) + ({{r}_{ - }} - r_{ - }^{'})}}{{2\sqrt 3 }}} \right] \\ \, \times {{I}_{0}}\left( {\sqrt {\frac{{(r_{ + }^{'} - {{r}_{ + }})({{r}_{ - }} - r_{ - }^{'})}}{3}} } \right), \\ \end{gathered} $$
((33))

where I0(z) is the Bessel function of the imaginary argument (see, for example, [22]; at that time, the corresponding notation had not been introduced, and Riemann represented I0 in the form of a power series).

Considering the Riemann formula (31) and expression (33) for the Riemann function, we can easily find the solution for potential W. It should be noted above all that substituting relations (32) into Eq. (31) and integrating by parts on account of the fact that W(0, 0) = 0, we can transform the Riemann formula to

$$\begin{gathered} W(P) = - \int\limits_A^O {R\left( {\frac{{\partial W}}{{\partial r_{ + }^{'}}} + \frac{W}{{2\sqrt 3 }}} \right)dr_{ + }^{'}} \\ \, + \int\limits_O^B {R\left( {\frac{{\partial W}}{{\partial r_{ - }^{'}}} - \frac{W}{{2\sqrt 3 }}} \right)dr_{ - }^{'}.} \\ \end{gathered} $$
((34))

Substituting boundary conditions (27) for W into this expression and performing simple transformations, we obtain

$$\begin{gathered} W({{r}_{ + }},{{r}_{ - }}) = \frac{l}{2}\exp \left( {\frac{{{{r}_{ - }} - {{r}_{ + }}}}{{2\sqrt 3 }}} \right) \\ \times \left\{ {\int\limits_{{{r}_{ + }}}^0 {\left( {\cosh \frac{r}{2} + \frac{2}{{\sqrt 3 }}\sinh \frac{r}{2}} \right)\exp \left( {\frac{r}{{\sqrt 3 }}} \right)} } \right. \\ \, \times {{I}_{0}}\left( {\sqrt {\frac{{(r - {{r}_{ + }}){{r}_{ - }}}}{3}} } \right)dr \\ \, + \int\limits_0^{{{r}_{ - }}} {\left( {\cosh \frac{r}{2} - \frac{2}{{\sqrt 3 }}\sinh \frac{r}{2}} \right)\exp \left( { - \frac{r}{{\sqrt 3 }}} \right)} \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}\, \times {{I}_{0}}\left( {\sqrt {\frac{{ - {{r}_{ + }}({{r}_{ - }} - r)}}{3}} } \right)dr} \right\}. \\ \end{gathered} $$
((35))

Together with formulas (20), this expression determines implicitly the dependence of Riemann invariants r± on x and t, which can also be used to determine the dependence of physical quantities on coordinate and time with the help of expression (10). The expression obtained for W is slightly more complicated that the analogous expression for the potential in the Khalatnikov solution [7] (see Section 4 below), but it is invariant with respect to transformation r+ → –r–, r‒ → –r+ corresponding to the sign reversal in the flow velocity. This implies the flow symmetry relative to reflection in plane x = 0, which does not hold in the form of the solution to the problem chosen by Khalatnikov. Let us obtain specific corollaries form the obtained solution.

3.3 Initial Stage of Evolution of the General Solution Domain

For short times t – tc ≪ tc elapsed after the instant of collision tc = l\(\sqrt 3 \) of expansion waves, Riemann invariants r± are small in absolute values, and we can expand derivatives ∂W/∂r± into a power series:

$$\begin{gathered} \frac{{\partial W}}{{\partial {{r}_{ + }}}} \approx l\left( { - \frac{1}{2} - \frac{{{{r}_{ + }} + {{r}_{ - }}}}{{2\sqrt 3 }} - \frac{{r_{ + }^{2}}}{8}} \right), \\ \frac{{\partial W}}{{\partial {{r}_{ - }}}} \approx l\left( {\frac{1}{2} - \frac{{{{r}_{ + }} + {{r}_{ - }}}}{{2\sqrt 3 }} + \frac{{r_{ - }^{2}}}{8}} \right). \\ \end{gathered} $$
((36))

Then relations (20) lead to the following expansions:

$$\begin{gathered} x \approx l({{r}_{ + }} + {{r}_{ - }})\left( {\frac{1}{{2\sqrt 3 }} - \frac{{5({{r}_{ + }} - {{r}_{ - }})}}{{24}}} \right), \\ t \approx l\left( {\sqrt 3 + \frac{{{{r}_{ - }} - {{r}_{ + }}}}{2} + \frac{{\sqrt 3 }}{8}(r_{ + }^{2} + r_{ - }^{2}) - \frac{{{{r}_{ + }}{{r}_{ - }}}}{{2\sqrt 3 }}} \right), \\ {\text{|}}{{r}_{ + }}{\text{|}},{{r}_{ - }} \ll 1. \\ \end{gathered} $$
((37))

At the instant of generation of the general solution for r+ = r– = 0, we have t = l\(\sqrt 3 \) as expected, and in the course of further evolution, we always have r+ = r– at the center of distribution for x = 0 (see Fig. 1).

At the right boundary between the general solution and the expansion wave, we have r+ = 0 and obtain the law of motion of this boundary in parametric form:

$$\begin{gathered} {{x}_{R}} \approx lr\left( {\frac{1}{{2\sqrt 3 }} + \frac{{5r}}{{24}}} \right), \\ t \approx l\left( {\sqrt 3 + \frac{r}{2} + \frac{{\sqrt 3 }}{8}{{r}^{2}}} \right),\quad r \ll 1, \\ \end{gathered} $$
((38))

i.e., we can write with the same degree of accuracy

$$\begin{gathered} {{x}_{R}}(t) \approx l\left\{ {\frac{t}{{l\sqrt 3 }} - 1 - 4{{{\left( {\frac{t}{{l\sqrt 3 }} - 1} \right)}}^{2}}} \right\}, \\ \frac{t}{{l\sqrt 3 }} - 1 \ll 1. \\ \end{gathered} $$
((39))

Consequently, in the main approximation, this boundary moves at the velocity of sound at the initial stage.

At the center of the distribution, for r– = –r+ ≡ r, we obtain

$$t \approx l\left( {\sqrt 3 + r + \frac{{\sqrt 3 }}{{12}}{{r}^{2}}} \right),$$

so that the temperature of the matter in this region first decreases in accordance with law

$$\begin{gathered} T = \exp \left( { - \frac{r}{{\sqrt 3 }}} \right) \approx 1 - \left( {\frac{t}{{l\sqrt 3 }} - 1} \right) + \frac{3}{4}{{\left( {\frac{t}{{l\sqrt 3 }} - 1} \right)}^{2}}, \\ \frac{t}{{l\sqrt 3 }} - 1 \ll 1. \\ \end{gathered} $$
((40))

3.4 Motion of General Solution Domain Boundaries

Since the flow is symmetric relative to plane x = 0, it is sufficient to consider the motion of right boundary xR(t), on which r+ = 0. Here, we already know the value of ∂W/∂r–\({{|}_{{{{r}_{ + }} = 0}}}\) from boundary condition (26), and the analogous limit for ∂W/∂r+ can easily be calculated with the help of solution (35). This gives (r = r–)

$$\begin{gathered} {{\left. {\frac{{\partial W}}{{\partial {{r}_{ + }}}}} \right|}_{{{{r}_{ + }} = 0}}} = \frac{l}{2}\exp \left( { - \frac{r}{{2\sqrt 3 }}} \right) \\ \times \left[ {\cosh \frac{r}{2} + \frac{1}{{\sqrt 3 }}\sinh \frac{r}{2} - 2\exp \left( {\frac{r}{{\sqrt 3 }}} \right)} \right], \\ {{\left. {\frac{{\partial W}}{{\partial {{r}_{ - }}}}} \right|}_{{{{r}_{ + }} = 0}}} = \frac{l}{2}\exp \left( { - \frac{r}{{2\sqrt 3 }}} \right) \\ \times \left( {\cosh \frac{r}{2} - \frac{1}{{\sqrt 3 }}\sinh \frac{r}{2}} \right). \\ \end{gathered} $$
((41))

Substituting these expressions into formula (20), we obtain the parametric law of motion for the right boundary:

$$\begin{gathered} {{x}_{R}} = l\left[ {1 + \exp \left( {\frac{r}{{\sqrt 3 }}} \right)\left( {\sqrt 3 \sinh \frac{r}{2} - \cosh \frac{r}{2}} \right)} \right], \\ t = l\exp \left( {\frac{r}{{\sqrt 3 }}} \right)\left( {\sqrt 3 \cosh \frac{r}{2} - \sinh \frac{r}{2}} \right). \\ \end{gathered} $$
((42))

For small r ≪ 1, these formulas are naturally reduced to (38), while for asymptotically long times t/l ≫ 1, when r ≫ 1, we obtain

$$\begin{gathered} x \approx l + t - l(\sqrt 3 + 1){{\left( {\frac{2}{{\sqrt 3 - 1}}\frac{t}{l}} \right)}^{{(2 - \sqrt 3 )/(2 + \sqrt 3 )}}}, \\ t \gg l. \\ \end{gathered} $$
((43))

It can be seen that although this boundary moves at a velocity close to the velocity of light, it lags behind the right boundary between the rarefaction wave and vacuum, which moves in accordance with the power law. However, the relative size of the domain occupied by the rarefaction wave decreases with time. We can easily write analogous expressions for the motion of the left boundary. The general pattern of motion of the edges of expansion waves and the general solution are shown in Fig. 3.

Fig. 3.
figure 3

(Color online) Solid curve depicts the motion of right boundary xR(t) in accordance with exact relations (42) with l = 1; dashed lines show the motion of the boundaries of the right rarefaction wave: its right edge propagates into vacuum with the velocity of light, while the left edge propagates to the bulk of matter with the velocity of sound (1/\(\sqrt 3 \)) until it collides with the left rarefaction wave at the center of distribution of matter (x = 0).

Full size image

It is natural to seek for the variation of the energy density at the boundary of the general solution domain as a function of proper time \(\bar {t}\) using the clock moving with this boundary:

$$\begin{gathered} \bar {t} = \int\limits_{\sqrt 3 l}^t {dt\sqrt {1 - {{{v}}^{2}}} = \int\limits_0^r {\frac{{dt{\text{/}}dr}}{{\cosh (r{\text{/}}2)}}dr} } \\ \approx l\frac{{\sqrt 3 + 1}}{2}\exp \left( {\frac{r}{{\sqrt 3 }}} \right), \\ \end{gathered} $$
((44))

where t = t(r) is expressed by the second expression in (42) and r = –2\(\sqrt 3 \)θ. Consequently, energy density ε = T4 = e4θ decreases upon an increase in the proper time in accordance with the quadratic law:

$$\varepsilon \approx \left( {1 + \frac{{\sqrt 3 }}{2}} \right){{\left( {\frac{l}{{\bar {t}}}} \right)}^{2}}.$$
((45))

3.5 Evolution of Energy Density at the Center of the Distribution

At the center of the distribution for x = 0, where r‒ = –r+ ≡ r, the second relation in (20) can be reduced after simple transformations to

$$\begin{gathered} t = l\sqrt 3 \exp \left( {\frac{r}{{\sqrt 3 }}} \right)\frac{d}{{dr}} \\ \times \left\{ {\exp \left( {\frac{r}{{\sqrt 3 }}} \right)\int\limits_0^r {\left( {\cosh \frac{{r{\kern 1pt} '}}{2} - \frac{1}{{\sqrt 3 }}\sinh \frac{{r{\kern 1pt} '}}{2}} \right)} } \right. \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}} \times \exp \left( { - \frac{{r{\kern 1pt} '}}{{\sqrt 3 }}} \right){{I}_{0}}\left( {\sqrt {\frac{{r(r - r{\kern 1pt} ')}}{3}} } \right)dr{\kern 1pt} '} \right\}, \\ \end{gathered} $$
((46))

which determines the dependence of parameter r on t. Since T = exp(θ) = exp(–r/\(\sqrt 3 \)) at this point, we can determine the time dependences of temperature and energy density at the center of the distribution. For asymptotically long times t ≫ l and for r ≫ 1, considering that the integral in expression (46) converges for r' ~ 1 owing to factor exp(–r'/\(\sqrt 3 \)) appearing in the integrand, we can use the following asymptotic approximation for the Bessel function [22]:

$${{I}_{0}}(z) \approx \frac{{{{e}^{z}}}}{{\sqrt {2\pi z} }},$$
((47))

so that

$$\begin{gathered} {{I}_{0}}\left( {\sqrt {\frac{{r(r - r{\kern 1pt} ')}}{3}} } \right) \approx \frac{{\exp \left( {\frac{r}{{\sqrt 3 }}} \right)\exp \left( { - \frac{{r{\kern 1pt} '}}{{2\sqrt 3 }}} \right)}}{{\sqrt {2\pi r{\text{/}}\sqrt 3 } }}, \\ r \gg r{\kern 1pt} '\sim 1, \\ \end{gathered} $$
((48))

and replace the upper integration limit by infinity. This gives

$$t \approx l\sqrt {\frac{2}{{3\pi ( - \theta )}}} {{e}^{{ - 3\theta }}},\quad {\text{|}}\theta {\text{|}} \gg 1.$$
((49))

We can solve this equation with logarithmic accuracy in –θ:

$$ - \theta \approx \frac{1}{3}\ln \left( {\frac{t}{l}} \right),$$

i.e.,

$$T \approx {{\left( {\frac{2}{{\pi \ln (t{\text{/}}l)}}} \right)}^{{1/6}}}{{\left( {\frac{l}{t}} \right)}^{{1/3}}}.$$
((50))

The energy density decreases with time as

$$\varepsilon = {{T}^{4}} \approx \frac{1}{{{{{[2\pi \ln (t{\text{/}}l)]}}^{{2/3}}}}}{{\left( {\frac{{2l}}{t}} \right)}^{{4/3}}},\quad t \gg l.$$
((51))

The law ε ∝ (l/t)4/3 was obtained by Landau [4] in the approximation disregarding the coefficients depending logarithmically on time.

3.6 Flow at Large Distances from the Boundary between the General Solution and Rarefaction Waves

Over long times, the temperature of the matter strongly decreases as compared to its initial value so that |θ| = |ln T| ≫ 1. If we are interested in the flow away from the boundaries of the general solution, on which one of the Riemann invariants vanishes, we can assume that both Riemann invariants r± = y ± \(\sqrt 3 \)θ are large in absolute value and use asymptotic expression (47) for evaluating the integrals in expression (35), replacing again the integration limits (r+ → –∞, r– → ∞). As a result, we arrive at the following simple expression for W:

$$\begin{gathered} W({{r}_{ + }},{{r}_{ - }}) \approx l \cdot {{3}^{{3/4}}}\sqrt {\frac{2}{\pi }} \frac{{{{{( - {{r}_{ + }}{{r}_{ - }})}}^{{1/4}}}}}{{{{r}_{ - }} - {{r}_{ + }} + 4\sqrt { - {{r}_{ + }}{{r}_{ - }}} }} \\ \times \exp \left[ {\frac{{{{{(\sqrt {{{r}_{ - }}} + \sqrt { - {{r}_{ + }}} )}}^{2}}}}{{2\sqrt 3 }}} \right]. \\ \end{gathered} $$
((52))

Omitting the preexponential factor, we return to the solution obtained by Landau [4, 10]. In evaluating the derivatives in the main approximation, it is sufficient to differentiate only the exponent because the power of the preexponential factor is not lowered in this case:

$$\begin{gathered} \frac{{\partial W}}{{\partial {{r}_{ + }}}} \approx - l\frac{{{{3}^{{1/4}}}}}{{\sqrt {2\pi } }}{{\left( {\frac{{{{r}_{ - }}}}{{ - {{r}_{ + }}}}} \right)}^{{1/4}}}\frac{{\sqrt {{{r}_{ - }}} + \sqrt { - {{r}_{ + }}} }}{{{{r}_{ - }} - {{r}_{ + }} + 4\sqrt { - {{r}_{ + }}{{r}_{ - }}} }} \\ \times \exp \left[ {\frac{{{{{(\sqrt {{{r}_{ - }}} + \sqrt { - {{r}_{ + }}} )}}^{2}}}}{{2\sqrt 3 }}} \right], \\ \frac{{\partial W}}{{\partial {{r}_{ - }}}} \approx l\frac{{{{3}^{{1/4}}}}}{{\sqrt {2\pi } }}{{\left( {\frac{{ - {{r}_{ + }}}}{{{{r}_{ - }}}}} \right)}^{{1/4}}}\frac{{\sqrt {{{r}_{ - }}} + \sqrt { - {{r}_{ + }}} }}{{{{r}_{ - }} - {{r}_{ + }} + 4\sqrt { - {{r}_{ + }}{{r}_{ - }}} }} \\ \times \exp \left[ {\frac{{{{{(\sqrt {{{r}_{ - }}} + \sqrt { - {{r}_{ + }}} )}}^{2}}}}{{2\sqrt 3 }}} \right]. \\ \end{gathered} $$
((53))

Substituting these expressions into (20), we obtain the dependence of the Riemann invariants on x and t. The intervals of variation of r+ and r– for a fixed value of time t can be determined from the second expression in (42):

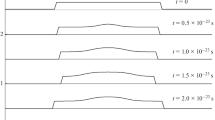
$$\begin{gathered} - {{r}_{m}} \lesssim {{r}_{ + }} \lesssim 0,\quad 0 \lesssim {{r}_{ - }} \lesssim {{r}_{m}}, \\ {{r}_{m}} \approx \frac{{2\sqrt 3 }}{{2 + \sqrt 3 }}\ln \left( {\frac{2}{{\sqrt 3 - 1}}\frac{t}{l}} \right). \\ \end{gathered} $$
((54))

Having fixed, for example, r+ in the indicated interval, we obtain the corresponding value of r– from the second equation in (20) for a given t, and then the corresponding value of x is defined by the first formula in (20). Therefore, we obtain the values of the Riemann invariants for a fixed t as functions of x, which determines the distributions of physical quantities in accordance with relations (10). The general form of the behavior of this solution was determined in [4, 10], where it was shown that the energy distribution lies in the ultrarelativistic region of the flow, while the number density of particles is concentrated at relatively low flow velocities. We will not consider here the details and only note that the distributions of physical quantities can now be determined with allowance for the preexponential factor. An example of the energy density distribution is shown in Fig. 4. Evolution time t = 1000 was chosen long for the Landau approximation to have a high accuracy for values of Riemann invariants r± ~ 5. However, for not very long times, the role of the preexponential factor becomes more significant, which affects the particle rapidity distribution being measured in experiment.

Fig. 4.
figure 4

(Color online) Solid curve shows the energy distribution ε(x) for x > 0 and t = 1000 for length l = 1 of the initial distribution for the asymptotic solution defined by function (52) and expansion wave. Dashed curve corresponds to the Landau approximation in the case when the preexponential factor is replaced by a constant coefficient selected so that the solutions coincide for x = 0.

Full size image

3.7 Rapidity Distribution

Rapidity distribution y for particles is an experimentally observable quantity [23], which is usually compared with the Gaussian distribution following from the Landau approximation. We will consider here more exact expressions taking into account the preexponential factor.

According to Landau [4], the entropy distribution is reproduced by the particle number distribution. For this reason, the rapidity distribution is proportional to the entropy distribution in each element of the matter at the instant when it is transformed into real hadrons at a temperature on the order of their mass [11]. In the proper coordinate system of an element of fluid, the entropy in a layer of thickness dx' is σdx' = σ(u0)'dx', where (u0)' = 1 is the temporal component of the 4-velocity. It is the product of the temporal component of the entropy flux vector and the spatial component of 4-vector dxi. We can assume that quantity (u0)'dx' in the 2D Minkowski geometry is an element of “area” A'01 = (u0)'dx' – (u1)'dt', where (u1)' = 0 in the proper coordinate system. This tensor component is invariant with respect to the Lorentz transformations; therefore, we obtain the following expression for the differential of the entropy in an arbitrary coordinate system:

$$dS = \sigma ({{u}^{0}}dx - {{u}^{1}}dt).$$
((55))

In the center-of-mass system, coordinates t and x are connected with flow parameters θ and y by relations

$$\begin{gathered} t = {{e}^{{ - \theta }}}\left( {\sinh y\frac{{\partial W}}{{\partial y}} - \cosh y\frac{{\partial W}}{{\partial \theta }}} \right), \\ x = {{e}^{{ - \theta }}}\left( {\cosh y\frac{{\partial W}}{{\partial y}} - \sinh y\frac{{\partial W}}{{\partial \theta }}} \right), \\ \end{gathered} $$
((56))

which can be obtained from formulas (20) using substitution (8). Substituting these relations into (56) and considering that σ ∝ T3 = e3θ, u0 = cosh y, and u1 = sinhy, we obtain

$$dS \propto {{e}^{{2\theta }}}\left\{ {\left( {\frac{{{{\partial }^{2}}W}}{{\partial {{y}^{2}}}} - \frac{{\partial W}}{{\partial \theta }}} \right)dy + \left( {\frac{{{{\partial }^{2}}W}}{{\partial \theta \partial y}} - \frac{{\partial W}}{{\partial y}}} \right)d\theta } \right\}.$$

At the instant of formation of free particles, we can disregard the variation of temperature, and their speed distribution repeats the entropy distribution

$$dN \propto dS \propto {{e}^{{2\theta }}}\left( {\frac{{{{\partial }^{2}}W}}{{\partial {{y}^{2}}}} - \frac{{\partial W}}{{\partial \theta }}} \right)dy,$$

where dN is the number of particles with rapidities in the interval (y, y + dy). In an asymptotic region away from the boundaries at which y = ±\(\sqrt 3 \)θ, simple calculations give

$$\begin{gathered} dN = G( - \theta )\frac{{\theta - \sqrt {{{\theta }^{2}} - {{y}^{2}}{\text{/}}3} }}{{{{{({{\theta }^{2}} - {{y}^{2}}{\text{/}}3)}}^{{1/4}}}(\theta - 2\sqrt {{{\theta }^{2}} - {{y}^{2}}{\text{/}}3} )}} \\ \times \exp \left[ {\theta + \sqrt {{{\theta }^{2}} - \frac{{{{y}^{2}}}}{3}} } \right]dy, \\ \end{gathered} $$
((57))

where G(–θ) is the normalization factor defined by condition \(\int_{\sqrt 3 \theta }^{ - \sqrt 3 \theta } {dN} \) = 1, and θ = lnT corresponds to the temperature of nuclear matter decay into individual particles. In fact, G(–θ) weakly depends on –θ and varies from G(3) ≈ 0.3797 to limiting value G(∞) = (1/2)\(\sqrt {3{\text{/}}(2\pi )} \) ≈ 0.3455 by only 4%. For –θ ≫ 1 and y ≪ |θ|, this distribution becomes Gaussian:

$$dN = \frac{1}{{\sqrt {6\pi ( - \theta )} }}\exp \left( { - \frac{{{{y}^{2}}}}{{6( - \theta )}}} \right)dy$$
((58))

in accordance with experiment at very high energies of colliding nuclei [23]. However, at moderate energies, it is apparently expedient to use more accurate formula (57).

4 COMPARISON WITH THE SOLUTION IN THE KHALATNIKOV FORM

Khalatnikov [7] used the coordinate system in which the right edge of the initial distribution of the matter is at point x = 0 (and not x = l as in our study). For the relation between x, t and variables θ, y, formulas (56) are used as before without the substitution x → x – l. For this reason, the Khalatnikov expression

$$\tilde {W}(\theta ,y) = l\sqrt 3 {{e}^{\theta }}\int\limits_{y/\sqrt 3 }^{ - \theta } {{{e}^{{2z}}}{{I}_{0}}(\sqrt {{{z}^{2}} - {{y}^{2}}{\text{/}}3} )} dz,$$
((59))

for the potential is not invariant to the speed sign reversal (y → –y), but has a simpler form as compared to our expression (35). The solution in Khalatnikov’s form written in terms of the Riemann invariants is

$$\begin{gathered} \tilde {W}({{r}_{ + }},{{r}_{ - }}) = l\sqrt 3 \exp \left( {\frac{{{{r}_{ + }} - {{r}_{ - }}}}{{2\sqrt 3 }}} \right) \\ \times \int\limits_{({{r}_{ - }} + {{r}_{ + }})/2\sqrt 3 }^{({{r}_{ - }} - {{r}_{ + }})/2\sqrt 3 } {{{e}^{{2z}}}{{I}_{0}}\left( {\sqrt {{{z}^{2}} - \frac{{{{{({{r}_{ + }} - {{r}_{ - }})}}^{2}}}}{{12}}} } \right)} dz. \\ \end{gathered} $$
((60))

Obviously, functions W in expression (35) and \(\tilde {W}\) in (60) do not coincide since they exhibit different symmetry properties. However, physical corollaries obtained from them are naturally identical. For example, on the right boundary between the general solution and an expansion wave for y = –\(\sqrt 3 \)θ, we obtain the derivatives

$$\begin{gathered} {{\left. {\frac{{\partial \tilde {W}}}{{\partial y}}} \right|}_{{y = - \sqrt 3 \theta }}} = - l{{e}^{{ - \theta }}}, \\ {{\left. {\frac{{\partial \tilde {W}}}{{\partial \theta }}} \right|}_{{y = - \sqrt 3 \theta }}} = - l\sqrt 3 {{e}^{{ - \theta }}}. \\ \end{gathered} $$
((61))

Substituting this derivatives into expression (56), we get the law of motion for the boundary, which coincides with (42) on account of placing the origin at point x = l. At the center of the distribution, for y = 0, formula (59) gives (r = –\(\sqrt 3 \)θ)

$$t = l\sqrt 3 \left\{ {\exp \left( {\frac{{2r}}{{\sqrt 3 }}} \right){{I}_{0}}\left( {\frac{r}{{\sqrt 3 }}} \right) - \int\limits_0^{r/\sqrt 3 } {{{e}^{{2z}}}{{I}_{0}}(z)dz} } \right\},$$
((62))

which differs in form from expression (46); however, the identity of these expressions can easily be verified numerically.

It should be noted that it is impossible to calculate the preexponential factor by simple substitution of asymptotic formula (47) into (60) because the integrand does not contain any longer the factor ensuring the convergence of the integral for finite z. Therefore, each representation has its own advantages in analysis of characteristic properties of the flow.

5 CONCLUSIONS

In this study, an alternative form of the exact solution to the problem of expansion of a layer of matter in relativistic fluid dynamics has been obtained. This problem was formulated by Landau [4], who obtained its asymptotic solution. The Riemann method [14, 15] applied to the Khalatnikov equation [7] makes it possible to find a solution satisfying the boundary conditions at the boundaries with rarefaction waves. Although this solution is physically equivalent to the Khalatnikov solution, its analytic form has certain advantages in analysis of the asymptotic nature of the flow with allowance for the preexponential factor. Comprehensive analysis of the main parameters of the flow in the entire range of its evolution has been performed.