Comparison of the Angles between the Magnetic Moment and Rotation Axis for Two Groups of Radio Pulsars

Abstract

Angles $\beta$ between the rotation axis and the magnetic moment are calculated in two groups of radio pulsars with different periods ($P > 2$ s and $0.1{\text{ s}} < P < 2$ s). Two methods have been used. The first method is based on the observed pulse widths and provides the minimum values of angle ${{\beta }_{1}}$. The distributions of these angles differ significantly for these groups of objects. The second method uses polarization data to calculate more accurate values ${{\beta }_{2}}$. There is a trend for bimodality in the distribution of ${{\beta }_{2}}$ values for pulsars with $P > 2$ s. The closeness of the mean ${{\beta }_{2}}$ values ($47.6^\circ$ for long-period pulsars and $35.6^\circ$ for sources with shorter periods) does not allow us to explain the previously discovered difference in the behavior of these two groups in the $(dP{\text{/}}dt){-} (P)$ diagram by a decrease in the role of magnetic dipole radiation due to a decrease in $\beta$. Our analysis showed that the observed difference can be explained by the different dependence of the pulsar wind and magnetic dipole braking on the period of the pulsar. The deceleration of pulsars with $P > 2$ s is mainly caused by the pulsar wind.

1 INTRODUCTION

One of the tools for analyzing the evolutionary paths of radio pulsars is still the study of the position of these objects in the $(dP{\text{/}}dt){-} (P)$ diagram, which describes the dependence of the derivative of the period between successive pulses on the period itself. This is due to the fact that these values are measured directly during sufficiently long observations and are not related to various assumptions about the nature of pulsars and their models. In [1], the corresponding diagrams were studied for three groups of pulsars with different period values: $P > 2$ s, $0.1{\text{ s}} < P < 2$ s, and $P < 0.1$ s. It was shown that the rotation of pulsars in the first group is slowed down by the removal of the angular momentum by relativistic particles (pulsar wind). In this case, the loss of rotational energy is described by the following expression [2]:

$$I\Omega \frac{{d\Omega }}{{dt}} = - \frac{{L_{p}^{{1/2}}BR_{*}^{3}{{\Omega }^{2}}}}{{{{{(6{{c}^{3}})}}^{{1/2}}}}}.$$

(1)

Here, $I$ is the moment of inertia of the neutron star, ${{R}_{*}}$ is its radius, $\Omega = 2\pi {\text{/}}P$ is the angular velocity of rotation, $B$ is the magnetic field on the surface, ${{L}_{p}}$ is the wind power, and $c$ is the speed of light.

In the second group, the pulsar wind is joined by the magnetic dipole radiation of the neutron star [3]:

$$I\Omega \frac{{d\Omega }}{{dt}} = - \frac{{{{B}^{2}}R_{*}^{6}{{\Omega }^{4}}{{{\sin }}^{2}}\beta }}{{6{{c}^{3}}}}.$$

(2)

The sources of the third group are decelerated by both mechanisms. It was suggested [1] that the contribution of the magnetic dipole radiation depends on the value of angle $\beta$ between the magnetic moment of a neutron star and its rotation axis. Indeed, it follows from expression (2) that the smaller this angle with other parameters being equal, the smaller the contribution of the magnetic dipole mechanism. To verify this assumption, it is necessary to calculate angle $\beta$ for pulsars with different periods and analyze the difference in this angle in different populations.

During all the years of pulsar studies, numerous attempts were made to calculate the $\beta$ angles using various methods [4–8]. It was also important to understand how this angle evolves with the age of the pulsar. In [9], a model of the magnetosphere was constructed, in which angle $\beta$ should increase with time, i.e., pulsars tend to become orthogonal rotators. However, further magnetohydrodynamic calculations [10] showed that the inclination of the magnetic moment to the axis of rotation decreases with age following a power law.

We analyze the difference in angle $\beta$ for two groups of pulsars with $P > 2$ s and $0.1{\text{ s}} < P < 2$ s. As for objects with $P < 0.1$ s, relativistic effects begin to play a role in them [11] and the calculation of $\beta$ may require other methods, which differ from those described in the next section.

2 METHODS USED TO CALCULATE ANGLE $\beta$

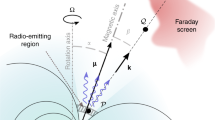
Further, we use the polar cap model shown in Fig. 1. Spherical trigonometry allows writing an equation that relates angles $\beta ,\zeta$, and $\theta$:

$$\cos \theta = \cos \beta \cos \zeta + \sin \beta \sin \zeta \cos \Phi .$$

(3)

Fig. 1.

Geometry of a pulsar radiation cone in the polar cap model: ${{\Phi }_{p}}$ is the observed pulse halfwidth, $\vec {\Omega }$ is the rotation axis of the pulsar, $\mu$ is the vector of the dipole magnetic moment, $L$ is the observer’s line of sight, $\theta$ is the angular radius of the radiation cone, $\zeta$ is the angle between the line of sight and the rotation axis, $\beta$ is the angle between the rotation axis and the magnetic moment vector, $\psi$ is the position angle of the radiation polarization plane, and $\Phi$ is the longitude.

Two more equations are needed to determine all three angles.

The simplest estimation method is associated with the assumption that the line of sight passes through the center of the radiation cone. In this case,

$$\beta = \zeta ,$$

(4)

and the statistical dependence of the pulse width at the 10% level on the period ${{W}_{{10}}}(P)$ can be used as the third equation, assuming that the observed profile width is related to the position of the radiation cone relative to the rotation axis. The real radius of the cone will correspond to $\beta = 90^\circ$, which in the (${{W}_{{10}}}){-} (P)$ diagram is determined by the lower boundary of the array of the observed values:

$$\theta = {{W}_{{10\min }}}(P){\text{/}}2.$$

(5)

This makes it possible to estimate angle $\beta$ based on Eq. (3) using the following expression:

$$\beta = \arcsin \left( {\frac{{\sin \frac{{{{W}_{{10\min }}}}}{4}}}{{\sin \frac{{{{W}_{{10}}}}}{4}}}} \right).$$

(6)

Since we assumed that the observed pulse broadening is associated solely with the approach of the radiation cone to the rotation axis of the pulsar, the values of the $\beta$ angle calculated by formula (6) represent the lower limits of this angle.

In what follows, we will use the pulsar parameters given in the ATNF catalog (latest version 1.67) [12].

It is generally accepted that the observed radio emission from pulsars is generated by the curvature radiation mechanism. In this case, the position angle $\psi$ of linear polarization is determined by the projection of the magnetic field, and its dependence on other angles can be represented as [13]

$$\tan \psi = \frac{{\sin \beta \sin \Phi }}{{\sin \zeta \cos \beta - \cos \zeta \sin \beta \cos \Phi }}.$$

(7)

The observational data show that the variation of the position angle for many pulsars is measured only within the main pulse in a small interval of longitudes $\Phi$. The rate of variation of the position angle reaches its maximum ${{(d\psi {\text{/}}d\Phi )}_{{\max }}}$ when the line of sight crosses the meridian at which the magnetic axis is located ($\Phi = 0$)

$${{\left| {\frac{{d\psi }}{{d\Phi }}} \right|}_{{\max }}} = \frac{{\sin \beta }}{{\sin (\zeta - \beta )}}.$$

(8)

The ${{\Phi }_{p}}$ value for the observed profile is determined by Eq. (3) and is given by the angle $\beta$ (apparent pulse broadening when approaching the axis of rotation) and the angular distance ($\zeta - \beta$) at which the line of sight intersects the radiation cone. The latter effect reduces the observable width ${{\Phi }_{p}}$. The contribution of each of these effects is not known in advance; therefore, on average, they can be considered equal, i.e., compensating each other. The $\theta (P)$ dependence can then be determined by a straight line inscribed in the ${{W}_{{10}}}(P)$ array using the least squares method, and we can set

$$\theta = \frac{{\langle {{W}_{{10}}}\rangle }}{2}.$$

(9)

Expressions (3), (8), and (9) form a system of three equations, which is reduced through transformations to an algebraic equation of the 4th degree:

$$\begin{gathered} C{{(1 - D)}^{2}}{{y}^{4}} + 2C(1 - D){{y}^{3}} \\ + \;[1 + 2{{C}^{2}}D(1 - D)]{{y}^{2}} + 2C(D - {{B}^{2}})y \\ \, + {{C}^{2}}{{D}^{2}} - {{B}^{2}}(1 + {{C}^{2}}) = 0, \\ \end{gathered} $$

(10)

where the following notations are introduced:

$$\begin{gathered} B = \cos \theta ,\quad C = {\text{|}}d\psi {\text{/}}d\Phi {\kern 1pt} {{{\text{|}}}_{{\max }}}, \\ D = \cos \langle {{W}_{{10}}}\rangle {\text{/}}2,\quad y = \cos \zeta . \\ \end{gathered} $$

(11)

Using expressions (11), relation (8) can be rewritten as

$$\tan \beta = \frac{{C{{{(1 - {{y}^{2}})}}^{{1/2}}}}}{{1 + Cy}}.$$

(12)

Solving Eq. (10) with respect to $y$, we find the required angle $\beta$ using (12).

Equation (10) has 4 solutions, from which 4 $\beta$ values are found. Some solutions may be complex and should be discarded. The sign of the derivative $C = (d\psi {\text{/}}d\Phi {{)}_{{\max }}}$ cannot be determined from the main pulse observations only, since the $d\Phi$ sign is not known, and the pulsar can rotate both clockwise and counterclockwise; therefore, it is necessary to solve the system of equations (10) and (12) at $C > 0$ and $C < 0$. Equation (10) can give a negative value $y = \cos \zeta$. This corresponds to $\zeta > 90^\circ$, which is quite possible in real pulsars.

In the calculation of angles $\beta$ by this method, we used the catalog of polarimetric data for 600 pulsars [14]. Objects in globular clusters and binary systems, where their parameters are affected by companions, were excluded. The following factors were also taken into account:

(1) The jump of the position angle by $180^\circ$ corresponds to its simple continuation, i.e., the polarimetric curves should be “sewn” at the discontinuity point. An example of this case is shown in Fig. 2.

Fig. 2.

Top: digitized profile of the position angle $\psi (\Phi )$ within the pulse of the pulsar J2346$-$0609 according to the catalog data [14]; bottom: “sewn” branches of $\psi (\Phi )$ and their fitting with a polynomial function: $\psi (\Phi )$ = $0.1014{{\Phi }^{3}}$ – $2.1966{{\Phi }^{2}}$ + $2.0967\Phi$ – $45.318$.

(2) Jumps by $90^\circ$ or smaller values indicate the presence of another mode (or other polarization modes), and such pulsars were excluded from further consideration.

(3) Sources with a stretched right “tail” in their pulses were also excluded. These “tails” are caused by scattering in the medium between the pulsar and the observer, which can significantly distort the polarization properties.

(4) On S-shaped $\psi (\Phi )$ dependences, the maximum derivative corresponds to the rectilinear part of the curve.

It should be noted that the solution of the system of equations (10) and (12) exists not for any values $B$, $C$, and $D$ obtained from observations. This may mean that the considered model of the behavior of the position angle does not work in certain pulsars.

Angle $\beta$ can be also determined using other methods [11], but we will restrict ourselves to those considered in this section.

3 RESULTS OF THE CALCULATIONS OF ANGLE $\beta$

As already mentioned, we use the data from the catalogs [12, 14] for the analysis.

For further calculations, we need to express the pulse width $W$ in degrees:

$${{W}_{{10}}}\;[^\circ ] = 360^\circ \frac{{{{W}_{{10}}}\;{\text{[ms]}}}}{{P\;{\text{[ms]}}}}.$$

(13)

Figure 3 shows the $({{W}_{{10}}}){-} (P)$ diagram for pulsars with $P > 2$ s.

Fig. 3.

Pulse width as a function of the period for radio pulsars with $P > 2$ s.

For the range $0.1 < P < 2$ s, the resulting sample contained 1381 pulsars with known ${{W}_{{10}}}$ values; in the range $P > 2$ s, the sample included 119 pulsars (see Tables 1, 2).

Table 1.   Angle β values for the sample of pulsars with periods $0.1 < P < 2$ s

Table 2.   Angle β values for the sample of pulsars with periods $P > 2$ s

For the sample with $P > 2$ s,

$$\log ({{W}_{{10\min }}}\;[^\circ ]) = - 0.582\log (P\;[{\text{s}}]) + 0.930,$$

(14)

or

$${{W}_{{10\min }}}\;[^\circ ]) = 8.5^\circ {{P}^{{ - 0.58}}}.$$

(15)

It should be emphasized that the ${{W}_{{10}}}(P)$ dependences can differ significantly between samples of pulsars, so we separately plotted the diagram similar to Fig. 3 for the sources with $0.1 < P < 2$ s (Fig. 4). The lower boundary for the sample with $0.1 < P < 2$ s is described by the equation

$$\log ({{W}_{{10\min }}}\;[^\circ ]) = - 0.062\log (P\;[{\text{s}}]) + 0.555,$$

(16)

hence

$${{W}_{{10\min }}}\;[^\circ ]) = 3.6^\circ {{P}^{{ - 0.06}}}.$$

(17)

Using expressions (14) and (17) and the catalog ${{W}_{{10}}}$ values, we calculated angles ${{\beta }_{1}}$ for the two groups of pulsars under study (see Table 1).

Fig. 4.

Pulse width as a function of the period for the sample with $0.1 < P < 2$ s.

Figure 5 shows the ${{\beta }_{1}}$ distribution histograms for two samples of pulsars normalized to the total number N of pulsars in the sample.

Fig. 5.

Angle ${{\beta }_{1}}$ distribution histograms for the pulsar samples with $0.1 < P < 2$ s and $P > 2$ s normalized to the number $N$ of pulsars in the sample.

To compare the statistical difference between the two distributions, the Kolmogorov–Smirnov test was used. The maximum difference ${{d}_{{\max }}}$ between the counts in two histograms was 0.285 (the counts were normalized to the number $N$ of pulsars in the samples). The Kolmogorov quantile was calculated using the formula

$$\lambda = {{d}_{{\max }}}\sqrt {\frac{{{{N}_{1}}{{N}_{2}}}}{{{{N}_{1}} + {{N}_{2}}}}} ,$$

(18)

where ${{N}_{1}}$ and ${{N}_{2}}$ are the numbers of pulsars in the first and second samples. The value of the Kolmogorov quantile $\lambda = 2.98$ calculated according to (18) means that the ${{\beta }_{1}}$ samples for pulsars with $0.1 < P < 2$ s and $P > 2$ s are statistically different with a probability $p = 0.99999$.

The resulting distributions can be fitted by Gaussians (Figs. 6, 7)

$$\begin{gathered} \frac{n}{{N({{\beta }_{1}})}} = (0.492 \pm 0.010) \\ \times \exp \left\{ { - \frac{{{{{({{\beta }_{1}} - (16.0 \pm 0.2))}}^{2}}}}{{2(8.7 \pm {{{0.4)}}^{2}}}}} \right\} \\ \end{gathered} $$

(19)

for the sample with $0.1 < P < 2$ s and

$$\begin{gathered} \frac{n}{{N({{\beta }_{1}})}} = (0.311 \pm 0.036) \\ \times \;\exp \left\{ { - \frac{{{{{({{\beta }_{1}} - (30.2 \pm 1.4))}}^{2}}}}{{2(11.7 \pm {{{3.1)}}^{2}}}}} \right\} \\ \end{gathered} $$

(20)

for pulsars with $P >$ 2 s.

Fig. 6.

Angle ${{\beta }_{1}}$ distribution for the sample of pulsars with $0.1 < P < 2$ s normalized to the number $N$ of pulsars in the sample.

Fig. 7.

Angle ${{\beta }_{1}}$ distribution for the sample of pulsars with $P > 2$ s normalized to the number $N$ of pulsars in the s-ample.

For the sample with $P > 2$ s, the distribution of angles ${{\beta }_{1}}$ shows a trend for bimodality. The statistical significance of the presence of bimodality was also estimated using the Kolmogorov–Smirnov test. The histogram was compared with two hypotheses: (1) the distribution can be fitted by a single Gaussian (monomodality); (2) the distribution was fitted by two Gaussians (bimodality). The comparison of the histogram with the hypothesis of monomodality yields the Kolmogorov quantile $\lambda = 0.49$, i.e., distributions do not differ significantly with probability $p = 0.97$. Comparing the histogram with the bimodal hypothesis, we obtained $\lambda = 0.33$, which means very good agreement with the model. The visually observed bimodality in the ${{\beta }_{1}}$ distribution for $P > 2$ s should be verified again with increased number of pulsars in this interval of periods. It should be emphasized that the currently observed angle ${{\beta }_{1}}$ values in the two maxima ($30.0^\circ \pm 1.2^\circ$ and $62.9^\circ \pm 3.5^\circ$) do not overlap with a very high probability (the corresponding variances $\sigma$ are $10.8^\circ \pm 0.4^\circ$and $6.0^\circ \pm 0.3^\circ$). In addition, the quantile for the bimodal representation is significantly smaller than for the monomodal representation. This means that the bimodal distribution fits the obtained ${{\beta }_{1}}$ values much better. For a monomodal distribution with $P > 2$ s, the Gaussian is described by Eq. (20), and for the bimodal hypothesis we can use the approximation:

$$\begin{gathered} \frac{{n({{\beta }_{1}})}}{N} = {{A}_{1}}\exp \left( { - \frac{1}{2}{{{\left( {\frac{{{{\beta }_{1}} - {{m}_{1}}}}{{{{\sigma }_{1}}}}} \right)}}^{2}}} \right) \\ + \;{{A}_{2}}\exp \left( { - \frac{1}{2}{{{\left( {\frac{{{{\beta }_{1}} - {{m}_{2}}}}{{{{\sigma }_{2}}}}} \right)}}^{2}}} \right), \\ \end{gathered} $$

$$\begin{gathered} {{A}_{1}} = 0.321 \pm 0.032,\quad {{m}_{1}} = 30.0 \pm 1.2, \\ {{\sigma }_{1}} = 10.8 \pm 0.4, \\ \end{gathered} $$

(21)

$$\begin{gathered} {{A}_{2}} = 0.073 \pm 0.003,\quad {{m}_{2}} = 62.9 \pm 3.5, \\ {{\sigma }_{1}} = 6.0 \pm 0.3. \\ \end{gathered} $$

Figures 8 and 9 show the $\langle {{W}_{{10}}}\rangle (P)$ dependences obtained for both samples of pulsars ($0.1 < P < 2$ s and $P > 2$ s). For the sample with $0.1 < P < 2$ s

$$\log (\langle {{W}_{{10}}}\;[^\circ ]\rangle (P)) = - 0.088\log (P\;[{\text{s}}]) + 1.303,$$

(22)

which corresponds to

$$\langle {{W}_{{10}}}\rangle = 20.1^\circ {{P}^{{ - 0.09}}}.$$

(23)

For the sample with $P > 2$ s,

$$\log (\langle {{W}_{{10}}}\;[^\circ ]\rangle (P)) = - 0.998\log (P\;[{\text{s}}]) + 1.559,$$

(24)

hence

$$\langle {{W}_{{10}}}\rangle = 36.2^\circ {\text{/}}P.$$

(25)

Since the number of pulsars in the Johnston and Kerr database [14] is several times less than the volume of the ATNF database, the cross-comparison of the catalogs led to a significant reduction in the size of the samples. Further selection of the polarization curves in accordance with the criteria mentioned above reduced the sample size even further. The final analysis included 93 pulsars for the sample with $0.1 < P <$ 2 s and 9 pulsars for the sample with $P > 2$ s. The solution of the 4th degree equation gives real roots not for any values $B$, $C$, and $D$, obtained from observations, so the final analysis included 70 pulsars with $0.1 < P <$ 2 s and 6 pulsars for the sample with $P >$ 2 s. The $\beta$ angle values calculated by this method (obtained from the solution of Eq. (10)), are denoted as ${{\beta }_{2}}$. The histograms of the angle ${{\beta }_{2}}$ distributions constructed for the two samples are shown in Fig. 10. The statistical difference between the two distributions was again compared using the Kolmogorov–Smirnov test. The value of the Kolmogorov quantile $\lambda = 0.41$ calculated using formula (18) shows that the ${{\beta }_{2}}$ samples for pulsars with $0.1 < P < 2$ s and $P > 2$ s are statistically indistinguishable with a probability $p = 0.996$. This is possibly due to the very small size of the sample with $P > 2$ s.

Fig. 8.

$\langle {{W}_{{10}}}\rangle$ as a function of period $P$ for the sample with $0.1 < P < 2$ s.

Fig. 9.

$\langle {{W}_{{10}}}\rangle$ as a function of period $P$ for the sample with $P > 2$ s.

Fig. 10.

Angle ${{\beta }_{2}}$ distribution histograms for the samples of pulsars with $0.1 < P < 2$ s and $P > 2$ s normalized to the number $N$ of pulsars in the samples.

For the sample with $0.1 < P < 2$ s, the distribution of angles ${{\beta }_{2}}$ shows visual signs of bimodality (see Fig. 11). Statistical analysis of the reliability of the presence of bimodality was carried out according to the method described in the previous section. For the case of comparing the histogram with the monomodality hypothesis, the Kolmogorov quantile $\lambda = 0.34$, i.e., the distributions do not differ significantly. Thus, the visually observed bimodality in the ${{\beta }_{2}}$ distribution for $0.1 < P < 2$ s is not confirmed in terms of statistical significance. For the monomodal distribution of this sample, $\langle {{\beta }_{2}}\rangle = 35.6^\circ \pm 4.3^\circ$ ($\sigma = 28.8^\circ \pm 4.1^\circ$).

Fig. 11.

Angle ${{\beta }_{2}}$ distribution for the sample of pulsars with $0.1 < P < 2$ s normalized to the number $N$ of pulsars in the sample.

The fitting of the ${{\beta }_{2}}$ distribution with the Gaussian function for the sample with $P >$ 2 s gives the mean value $\langle {{\beta }_{2}}\rangle = 47.6^\circ \pm 5.9^\circ$ ($\sigma = 17.8^\circ \pm 8.0^\circ$), which is shown in Fig. 12. Figures 13 and 14 show the ${{\beta }_{1}}$ and ${{\beta }_{2}}$ distributions for the two groups of samples. The statistical analysis using the Kolmogorov–Smirnov test showed that for pulsar samples with $0.1 < P < 2$ s, the ${{\beta }_{1}}$ and ${{\beta }_{2}}$ distributions differ significantly ($\lambda = 2.45$, $p = 0.99999$), while for the ${{\beta }_{1}}$ and ${{\beta }_{2}}$ distributions of objects with $P > 2$ s, the statistical difference is small ($\lambda = 0.80$, $p = 0.4559$), which may also be due to the small size of the sample with $P > 2$ s for ${{\beta }_{2}}$.

Fig. 12.

Angle ${{\beta }_{2}}$ distribution for the sample of pulsars with $P > 2$ s normalized to the number $N$ of pulsars in the sample.

Fig. 13.

Distribution histograms of angles ${{\beta }_{1}}$ and ${{\beta }_{2}}$ for the samples of pulsars with $0.1 < P < 2$ s normalized to the number $N$ of pulsars in the sample.

Fig. 14.

Distribution histograms of angles ${{\beta }_{1}}$ and ${{\beta }_{2}}$ for the samples of pulsars with $P > 2$ s normalized to the number $N$ of pulsars in the sample.

Figure 15 depicts the ${{\beta }_{1}}{-} {{\beta }_{2}}$ diagrams for both samples. The bisector shown by the red line indicates the region on the graph where both methods should give the same result. As can be seen from the graphs, all ${{\beta }_{2}}$ values are greater than the corresponding ${{\beta }_{1}}$ values (with the exception of four pulsars, for which they can be considered equal within the error limits). The ${{\beta }_{1}}$ distribution is noticeably narrower than ${{\beta }_{2}}$ (almost three times in the $\sigma$ value for pulsars with $0.1 < P < 2$ s).

Fig. 15.

Angle ${{\beta }_{1}}$ and ${{\beta }_{2}}$ values for the samples of pulsars with $0.1 < P < 2$ s and $P > 2$ s.

The ${{\beta }_{1}}$ values obtained on the basis of formula (6) should be considered as the lower limits of the angle between the rotation axis and the vector of the magnetic moment of the pulsar.

4 DISCUSSION AND CONCLUSIONS

The main goal of our study was to test the possibility of explaining the different behavior of two groups of pulsars with periods $P > 2$ s and $0.1 < P < 2$ s in the $(dP{\text{/}}dt){-} (P)$ diagram by the difference in the inclination angle of their magnetic moment to the rotation axis. This possibility was proposed in [1]. Our analysis showed that no such difference was observed. The average values of the lower estimates of angle $\langle {{\beta }_{1}}\rangle = 30.2^\circ$ for pulsars with $P > 2$ s and $16.0^\circ$ for objects with shorter periods overlap taking into account their variances ($\sigma = 11.7^\circ$ and $8.7^\circ$, respectively). The same can be said about more accurate estimates of angle $\beta$ $\langle {{\beta }_{2}}\rangle = 47.6^\circ$ and $35.6^\circ$, $\sigma = 9.5^\circ$ and $10.2^\circ$. In both methods, the average value of angle $\beta$ for pulsars with longer periods turns out to be larger, which, in accordance with Eq. (2), should rather indicate an increase in their magnetic dipole radiation. Therefore, it is necessary to look for other causes of the observed difference.

We compared the role of two deceleration mechanisms associated with the pulsar wind and magnetic radiation. The corresponding loss of angular momentum is described by Eqs. (1) and (2) above. The ratio of the efficiencies of each of the mechanisms is determined by the following expression:

$$\xi = \frac{{{{{(6{{L}_{p}}{{c}^{3}})}}^{{1/2}}}{{P}^{2}}}}{{4{{\pi }^{2}}BR_{*}^{3}{{{\sin }}^{2}}\beta }}.$$

(26)

Assuming that all the characteristic parameters of the pulsars ($L,\;B,\;{{R}_{*}}$, and $\beta$) in the two groups are the same, we arrive at the relation

$$\frac{{{{\xi }_{2}}}}{{{{\xi }_{1}}}} = \frac{{P_{2}^{2}}}{{P_{1}^{2}}}.$$

(27)

The mean periods for the two groups are approximately 2.5 and 0.5 s. This means that the losses due to the pulsar wind in long-period pulsars should be 25 times higher than the magnetic dipole losses. As shown in [1], this is indeed observed.

(1) Our analysis shows that the distribution of $\beta$ angles calculated by the observed pulse profile width (${{\beta }_{1}}$) confirms the statistically significant difference in the distributions for the pulsar samples with $0.1 < P < 2$ s (sample size $N = 1381$ pulsars) and $P > 2$ s ($N = 119$). At the same time, for the sample with $0.1 < P < 2$ s, the average value $\langle {{\beta }_{1}}\rangle =$ 16.0° ± 0.2° ($\sigma = 8.7^\circ \pm 0.3^\circ$), and for $P > 2$ s, $\langle {{\beta }_{1}}\rangle =$ 30.2° ± 1.4° ($\sigma = 11.7^\circ \pm 3.1^\circ$).

The visually observed bimodality in the ${{\beta }_{1}}$ distribution for the sample with $P > 2$ s has a low statistical significance according to the Kolmogorov–Smirnov test. However, the Kolmogorov quantile for the bimodal representation is much smaller than for the monomodal one. This means that the bimodal distribution fits the obtained ${{\beta }_{1}}$ values better.

(2) The analysis using the maximum derivative of the position angle of polarization yields distributions of angles ${{\beta }_{2}}$ that differ noticeably from the corresponding distributions for ${{\beta }_{1}}$: $\langle {{\beta }_{2}}\rangle = 35.6^\circ \pm 4.3^\circ$ ($\sigma = 28.8^\circ \pm 4.1^\circ$) for the pulsar sample with $0.1 < P < 2$ s ($N = 70$) and $\langle {{\beta }_{2}}\rangle = 47.6^\circ \pm 5.9^\circ$ ($\sigma = 17.8^\circ \pm 8.0^\circ$) for the sample with $P > 2$ s ($N = 6$). The ${{\beta }_{2}}$ distributions in the two samples are not statistically different according to the Kolmogorov–Smirnov test, which may be due to the small sample size for $P > 2$ s. The emerging bimodality in the ${{\beta }_{2}}$ distribution for the sample with $0.1 < P < 2$ s turns out to be statistically insignificant according to the Kolmogorov–Smirnov test.

(3) The ${{\beta }_{1}}$ and ${{\beta }_{2}}$ distributions for the samples with $0.1 < P < 2$ s differ significantly, while the ${{\beta }_{1}}$ and ${{\beta }_{2}}$ distributions for the samples with $P > 2$ s are not statistically distinguishable, which can also be due to the small size of the sample with $P > 2$ s for ${{\beta }_{2}}$.

(4) All ${{\beta }_{2}}$ values are greater than or equal to the corresponding ${{\beta }_{1}}$ values (within error), which confirms that the ${{\beta }_{1}}$ values should be considered as the lower limits of angle $\beta$ between the axis of rotation and the magnetic moment vector of the pulsar.

(5) The different behavior of radio pulsars with periods $P > 2$ s and $0.1 < P < 2$ s found earlier in the $(dP{\text{/}}dt){-} (P)$ diagram is explained by the different period dependence of the losses for the pulsar wind and magnetic dipole braking and by much faster removal of angular momentum by relativistic particles in long-period pulsars.

To confirm the results obtained in this study, in particular, more definite judgments about the emerging bimodalities in the distributions of angle $\beta$, it is necessary to expand the sample of pulsars with periods $P > 2$ s.