INTRODUCTION

Methods based on synchronous multiple-microphone measurements are used to identify sound sources in acoustics [1]. We should note the algorithms of beamforming type that have broadly developed with application to problems of aeroacoustics [2]. In the classical conventional beamforming (CB) algorithm, monopoles are used as source models. Such a choice of source type for the inverse problem of determining the amplitudes makes sense if the characteristics of the studied sound field are a priori unknown and the region of generation of the most intense radiation relative to the position of the microphone array needs to be determined. In the course of further development of this line of research, a problem formulation arose within which it makes sense to discriminate the source types and consider acoustic sources of complex structure [3–7]. Due to the mathematical ill-posedness of the inverse problem for determining the field of sources by an induced sound field [8], there is still no adequate natural mathematical formulation in which a unified model of sources composed of sources of different type can be considered. The existing algorithms have rigorous limitations in their applicability and usually use a set of sources limited by a single multipole type [6, 7, 9]. In this work, we propose a new theoretical approach to the problem of determining the field of amplitudes of acoustic sources. The main advantage of the proposed method is the well-posedness of the inverse problem. In particular, the method allows taking into account sources of various types in a unified model of sources. The peculiarity of this method lies in the transition to consideration of correlation characteristics of the studied acoustic fields and sources inducing them. When a system of sources is imposed by the delta-correlation conditions, the problem acquires completely different mathematical properties that are not inherent to the process described by the original wave equation. Thus, the operator entering the formulation of the inverse problem of source identification is no longer degenerate. This approach allows discriminating different types of sources within the framework of the problem of simultaneous recognition. The method is verified using an example of determining the monopole and dipole components of the field of acoustic sources and allows separating both components with correct values of the spatial distribution of amplitudes.

CORRELATION-PROBLEM FORMULATION OF ACOUSTIC-SOURCE IDENTIFICATION

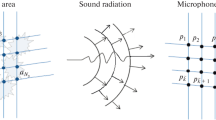
Consider the scheme of microphone measurements of a sound field propagating from the region of generation, where the supposed sound sources are situated (Fig. 1).

Fig. 1.
figure 1

Scheme of multiple-microphone synchronous measurements.

Full size image

The region from which the acoustic radiation emerges is divided into a discrete grid, each node of which is put in correspondence to a priori unknown amplitude \({{a}_{k}}\). Then, the Fourier image of the pressure induced at the \(i\)th microphone of the array is represented in the form

$${{p}_{i}} = \sum\limits_{k = 1}^{{{N}_{s}}} {{{G}_{{ik}}}{{a}_{k}}} ,$$
(1)

where Gik is the signal induced by a single source located in the kth node of the grid of sources at the ith microphone (the columns of the matrix Gik = (q1|q2|…|qNs) are called “directors,” representing the pressures induced by the corresponding single sound sources located in the nodes of the source grid at the microphones of the array).

In applied problems, it is often impossible to directly seek the numerical solution to system (1). The detailed numerical analysis of the conditions to the field of sources and to the geometry of the microphone array in which system of equations (1) is well-posed is provided in work [10].

Consider the spectral matrix \(\overline {{{p}_{i}}p_{j}^{ * }} \); here, \(\overline {{\text{ }}\bullet {\text{ }}} \) means averaging over realizations:

$$\overline {{{p}_{i}}p_{j}^{ * }} = \sum\limits_{k = 1,p = 1}^{{{N}_{s}}} {{{G}_{{ik}}}\overline {{{a}_{k}}a_{p}^{ * }} G_{{jp}}^{ * }} .$$
(2)

This expression in the matrix form becomes

$$C = GA{{G}^{H}},$$
(3)

where \({{C}_{{ij}}} = \overline {{{p}_{i}}p_{j}^{ * }} \) and \({{A}_{{kp}}} = \overline {{{a}_{k}}a_{p}^{ * }} \).

To determine the positions of sources in space and the correlation relationships between them (in particular, their amplitudes), we need to solve matrix equation (3). For this purpose, it is convenient to use the technique of the Kronecker product of matrices [11]. In this case, the system takes the form

$$\tilde {C} = (G \otimes G*)\tilde {A}{\text{ }},$$
(4)

where

$$\begin{gathered} \tilde {C} = \left( {\begin{array}{*{20}{c}} {\overline {{{{\left| {{{p}_{1}}} \right|}}^{2}}} } \\ {\overline {{{p}_{1}}p_{2}^{ * }} } \\ \vdots \\ {\overline {{{p}_{1}}p_{{{{N}_{m}}}}^{ * }} } \\ {\overline {{{p}_{2}}p_{1}^{ * }} } \\ {\overline {{{{\left| {{{p}_{2}}} \right|}}^{2}}} } \\ \vdots \\ {\overline {{{p}_{2}}p_{{{{N}_{m}}}}^{ * }} } \\ \vdots \\ {\overline {{{p}_{{{{N}_{m}}}}}p_{1}^{ * }} } \\ \vdots \\ {\overline {{{{\left| {{{p}_{{{{N}_{m}}}}}} \right|}}^{2}}} } \end{array}} \right),\,\,\,\,\widetilde A = \left( {\begin{array}{*{20}{c}} {\overline {{{{\left| {{{a}_{1}}} \right|}}^{2}}} } \\ {\overline {{{a}_{1}}a_{2}^{ * }} } \\ \vdots \\ {\overline {{{a}_{1}}a_{{{{N}_{s}}}}^{ * }} } \\ {\overline {{{a}_{2}}a_{1}^{ * }} } \\ {\overline {{{{\left| {{{a}_{2}}} \right|}}^{2}}} } \\ \vdots \\ {\overline {{{a}_{2}}a_{{{{N}_{s}}}}^{ * }} } \\ \vdots \\ {\overline {{{a}_{{{{N}_{s}}}}}a_{1}^{ * }} } \\ \vdots \\ {\overline {{{{\left| {{{a}_{{{{N}_{s}}}}}} \right|}}^{2}}} } \end{array}} \right), \\ G \otimes G*\,\, = \left( {\begin{array}{*{20}{c}} {{{G}_{{11}}}G_{{11}}^{ * }}&{{{G}_{{11}}}G_{{12}}^{ * }}& \cdots &{{{G}_{{11}}}G_{{1{{N}_{s}}}}^{ * }}&{{{G}_{{12}}}G_{{11}}^{ * }}&{{{G}_{{12}}}G_{{12}}^{ * }}& \cdots &{{{G}_{{12}}}G_{{1{{N}_{s}}}}^{ * }}& \cdots &{{{G}_{{1{{N}_{s}}}}}G_{{11}}^{ * }}& \cdots &{{{G}_{{1{{N}_{s}}}}}G_{{1{{N}_{s}}}}^{ * }} \\ {{{G}_{{11}}}G_{{21}}^{ * }}&{{{G}_{{11}}}G_{{22}}^{ * }}& \cdots &{{{G}_{{11}}}G_{{2{{N}_{s}}}}^{ * }}&{{{G}_{{12}}}G_{{21}}^{ * }}&{{{G}_{{12}}}G_{{22}}^{ * }}& \cdots &{{{G}_{{12}}}G_{{2{{N}_{s}}}}^{ * }}& \cdots &{{{G}_{{1{{N}_{s}}}}}G_{{21}}^{ * }}& \cdots &{{{G}_{{1{{N}_{s}}}}}G_{{2{{N}_{s}}}}^{ * }} \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {{{G}_{{11}}}G_{{{{N}_{m}}1}}^{ * }}&{{{G}_{{11}}}G_{{{{N}_{m}}2}}^{ * }}& \cdots &{{{G}_{{11}}}G_{{{{N}_{m}}{{N}_{s}}}}^{ * }}&{{{G}_{{12}}}G_{{{{N}_{m}}1}}^{ * }}&{{{G}_{{12}}}G_{{{{N}_{m}}2}}^{ * }}& \cdots &{{{G}_{{12}}}G_{{{{N}_{m}}{{N}_{s}}}}^{ * }}& \cdots &{{{G}_{{1{{N}_{s}}}}}G_{{{{N}_{m}}1}}^{ * }}& \cdots &{{{G}_{{1{{N}_{s}}}}}G_{{{{N}_{m}}{{N}_{s}}}}^{ * }} \\ {{{G}_{{21}}}G_{{11}}^{ * }}&{{{G}_{{21}}}G_{{12}}^{ * }}& \cdots &{{{G}_{{21}}}G_{{1{{N}_{s}}}}^{ * }}&{{{G}_{{22}}}G_{{11}}^{ * }}&{{{G}_{{22}}}G_{{12}}^{ * }}& \cdots &{{{G}_{{22}}}G_{{1{{N}_{s}}}}^{ * }}& \cdots &{{{G}_{{2{{N}_{s}}}}}G_{{11}}^{ * }}& \cdots &{{{G}_{{2{{N}_{s}}}}}G_{{1{{N}_{s}}}}^{ * }} \\ {{{G}_{{21}}}G_{{21}}^{ * }}&{{{G}_{{21}}}G_{{22}}^{ * }}& \cdots &{{{G}_{{21}}}G_{{2{{N}_{s}}}}^{ * }}&{{{G}_{{22}}}G_{{21}}^{ * }}&{{{G}_{{22}}}G_{{22}}^{ * }}& \cdots &{{{G}_{{22}}}G_{{2{{N}_{s}}}}^{ * }}& \cdots &{{{G}_{{2{{N}_{s}}}}}G_{{21}}^{ * }}& \cdots &{{{G}_{{2{{N}_{s}}}}}G_{{2{{N}_{s}}}}^{ * }} \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {{{G}_{{21}}}G_{{{{N}_{m}}1}}^{ * }}&{{{G}_{{21}}}G_{{{{N}_{m}}2}}^{ * }}& \cdots &{{{G}_{{21}}}G_{{{{N}_{m}}{{N}_{s}}}}^{ * }}&{{{G}_{{22}}}G_{{{{N}_{m}}1}}^{ * }}&{{{G}_{{22}}}G_{{{{N}_{m}}2}}^{ * }}& \cdots &{{{G}_{{22}}}G_{{{{N}_{m}}{{N}_{s}}}}^{ * }}& \cdots &{{{G}_{{2{{N}_{s}}}}}G_{{{{N}_{m}}1}}^{ * }}& \cdots &{{{G}_{{2{{N}_{s}}}}}G_{{{{N}_{m}}{{N}_{s}}}}^{ * }} \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {{{G}_{{{{N}_{m}}1}}}G_{{11}}^{ * }}&{{{G}_{{{{N}_{m}}1}}}G_{{12}}^{ * }}& \cdots &{{{G}_{{{{N}_{m}}1}}}G_{{1{{N}_{s}}}}^{ * }}&{{{G}_{{{{N}_{m}}2}}}G_{{11}}^{ * }}&{{{G}_{{{{N}_{m}}2}}}G_{{12}}^{ * }}& \cdots &{{{G}_{{{{N}_{m}}2}}}G_{{1{{N}_{s}}}}^{ * }}& \cdots &{{{G}_{{{{N}_{m}}{{N}_{s}}}}}G_{{11}}^{ * }}& \cdots &{{{G}_{{{{N}_{m}}{{N}_{s}}}}}G_{{1{{N}_{s}}}}^{ * }} \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots \\ {{{G}_{{{{N}_{m}}1}}}G_{{{{N}_{m}}1}}^{ * }}&{{{G}_{{{{N}_{m}}1}}}G_{{{{N}_{m}}2}}^{ * }}& \cdots &{{{G}_{{{{N}_{m}}1}}}G_{{{{N}_{m}}{{N}_{s}}}}^{ * }}&{{{G}_{{{{N}_{m}}2}}}G_{{{{N}_{m}}1}}^{ * }}&{{{G}_{{{{N}_{m}}2}}}G_{{{{N}_{m}}2}}^{ * }}& \cdots &{{{G}_{{{{N}_{m}}2}}}G_{{{{N}_{m}}{{N}_{s}}}}^{ * }}& \cdots &{{{G}_{{{{N}_{m}}{{N}_{s}}}}}G_{{{{N}_{m}}1}}^{ * }}& \cdots &{{{G}_{{{{N}_{m}}{{N}_{s}}}}}G_{{{{N}_{m}}{{N}_{s}}}}^{ * }} \end{array}} \right). \\ \end{gathered} $$

The issue of ill-posedness of the inverse problem of determining the source field by an induced sound radiation remains present in this formulation. Let us show that, when we switch to consideration of acoustic fields induced by delta-correlated fields, the issue of ill-posedness disappears.

Assuming there to be a delta correlation of sources (the matrix of amplitudes acquires diagonal form \({{A}_{{kp}}} = \overline {{{a}_{k}}a_{p}^{ * }} = \overline {a_{k}^{2}} {{\delta }_{{kp}}}\)), we can simplify relation (4), eliminating a large number of relations expressing the correlations between different sources:

$${{\tilde {C}}_{{reduce}}} = {{(G \otimes G*)}_{{{\text{reduce}}}}}{{\tilde {A}}_{{{\text{uncorrelated}}}}},$$
(5)

where

$${{\tilde {C}}_{{{\text{reduce}}}}} = \left( {\begin{array}{*{20}{c}} {\overline {{{{\left| {{{p}_{1}}} \right|}}^{2}}} } \\ {\overline {{{p}_{1}}p_{2}^{ * }} } \\ \vdots \\ {\overline {{{p}_{1}}p_{{{{N}_{m}}}}^{ * }} } \\ {\overline {{{{\left| {{{p}_{2}}} \right|}}^{2}}} } \\ \vdots \\ {\overline {{{p}_{2}}p_{{{{N}_{m}}}}^{ * }} } \\ \vdots \\ {\overline {{{{\left| {{{p}_{{{{N}_{m}}}}}} \right|}}^{2}}} } \end{array}} \right),\,\,\,\,{{\tilde {A}}_{{{\text{uncorrelated}}}}}\left( {\begin{array}{*{20}{c}} {\overline {a_{1}^{2}} } \\ {\overline {a_{2}^{2}} } \\ \vdots \\ {\overline {a_{{{{N}_{s}}}}^{2}} } \end{array}} \right),\,\,{{(G \otimes G*)}_{{{\text{reduce}}}}}\, = \,\left( {\begin{array}{*{20}{c}} {{{G}_{{11}}}G_{{11}}^{ * }}&{{{G}_{{12}}}G_{{12}}^{ * }}& \cdots &{{{G}_{{1{{N}_{s}}}}}G_{{1{{N}_{s}}}}^{ * }} \\ {{{G}_{{11}}}G_{{21}}^{ * }}&{{{G}_{{12}}}G_{{22}}^{ * }}& \cdots &{{{G}_{{1{{N}_{s}}}}}G_{{2{{N}_{s}}}}^{ * }} \\ \vdots & \vdots & \ddots & \vdots \\ {{{G}_{{11}}}G_{{{{N}_{m}}1}}^{ * }}&{{{G}_{{12}}}G_{{{{N}_{m}}2}}^{ * }}& \cdots &{{{G}_{{1{{N}_{s}}}}}G_{{{{N}_{m}}{{N}_{s}}}}^{ * }} \\ {{{G}_{{21}}}G_{{21}}^{ * }}&{{{G}_{{22}}}G_{{22}}^{ * }}& \cdots &{{{G}_{{2{{N}_{s}}}}}G_{{2{{N}_{s}}}}^{ * }} \\ {{{G}_{{21}}}G_{{31}}^{ * }}&{{{G}_{{22}}}G_{{32}}^{ * }}& \cdots &{{{G}_{{2{{N}_{s}}}}}G_{{3{{N}_{s}}}}^{ * }} \\ \vdots & \vdots & \ddots & \vdots \\ {{{G}_{{21}}}G_{{{{N}_{m}}1}}^{ * }}&{{{G}_{{22}}}G_{{{{N}_{m}}2}}^{ * }}& \cdots &{{{G}_{{2{{N}_{s}}}}}G_{{{{N}_{m}}{{N}_{s}}}}^{ * }} \\ \vdots & \vdots & \ddots & \vdots \\ {{{G}_{{{{N}_{m}}1}}}G_{{{{N}_{m}}1}}^{ * }}&{{{G}_{{{{N}_{m}}2}}}G_{{{{N}_{m}}2}}^{ * }}& \cdots &{{{G}_{{{{N}_{m}}{{N}_{s}}}}}G_{{{{N}_{m}}{{N}_{s}}}}^{ * }} \end{array}} \right).$$

Note that, owing to the fact that the spectral matrix \(\overline {{{p}_{i}}p_{j}^{ * }} \) is Hermitian, in the reduced matrix \({{(G \otimes G*)}_{{{\text{reduce}}}}}\), in addition to the columns corresponding to correlation of different sources, we have also removed some rows that were different only in the complex conjugation and introducing no new information.

The obtained system of equations (5) is quasi-linear, because elements \({{\tilde {A}}_{{{\text{uncorrelated}}}}}\) are mean squares of the power of sources and cannot be negative, which is an substantial circumstance that is taken into account in the procedure for determining the unknowns.

System (5) has properties that differ from the properties of the original system (4). This allows correctly posing the problem of source identification in configurations (types of sources, region of their location, and geometry of microphone array) ill-posed within the original system for correlated sources. The difference of the operators present in problems (4) and (5) can be vividly seen using the example of a continuous model, where discretization by a grid of sources was not performed:

$$p({\mathbf{r}}) = \int G ({\mathbf{r}},{\mathbf{\xi }})a({\mathbf{\xi }})d{\mathbf{\xi }},$$
(6)
$$\overline {p({{{\mathbf{r}}}_{1}})p{\text{*}}({{{\mathbf{r}}}_{2}})} = \int {G({{{\mathbf{r}}}_{1}},{{{\mathbf{\xi }}}_{1}})G{\text{*}}({{{\mathbf{r}}}_{2}},{{{\mathbf{\xi }}}_{2}})\overline {a({{{\mathbf{\xi }}}_{1}})a{\text{*}}({{{\mathbf{\xi }}}_{2}})} d{{{\mathbf{\xi }}}_{1}}d{{{\mathbf{\xi }}}_{2}}} ,$$
(7)
$$\overline {p({{{\mathbf{r}}}_{1}})p{\text{*}}({{{\mathbf{r}}}_{2}})} = \int {G({{{\mathbf{r}}}_{1}},{\mathbf{\xi }})G{\text{*}}({{{\mathbf{r}}}_{2}},{\mathbf{\xi }})\overline {{{{\left| {a({\mathbf{\xi }})} \right|}}^{2}}} d{\mathbf{\xi }}} {\text{ }},$$
(8)

where \(G({\mathbf{r}},{\mathbf{\xi }})\) is the Green’s function corresponding to the type of source.

Formula (6) is the solution to the wave equation. Formula (7) is the equation or correlations, an immediate consequence of the wave equation. Formula (8) describes the solution to the delta-correlated field of sources \(\overline {a({{{\mathbf{\xi }}}_{1}})a{\text{*}}({{{\mathbf{\xi }}}_{2}})} = \overline {{{{\left| {a({{{\mathbf{\xi }}}_{1}})} \right|}}^{2}}} \delta ({{{\mathbf{\xi }}}_{1}} - {{{\mathbf{\xi }}}_{2}})\). Uncorrelated sound sources (8), in contrast to correlated sources (6) and (7), cannot be nonradiating as a whole, because the energy transferred by the acoustic field through the surface covering the sources is equal to the sum of radiation energies from each individual source and can vanish only if there are no sources at all:

$$\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc} {\overline {{{{\left| {p({\mathbf{r}})} \right|}}^{2}}} } dS = \mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc} {\int {{{{\left| {G({\mathbf{r}},{\mathbf{\xi }})} \right|}}^{2}}\overline {{{{\left| {a({\mathbf{\xi }})} \right|}}^{2}}} d{\mathbf{\xi }}} } dS.$$
(9)

If \(\int {\overline {{{{\left| {a({\mathbf{\xi }})} \right|}}^{2}}} d{\mathbf{\xi }}} > 0\), then \(\mathop{{\int\!\!\!\!\!\int}\mkern-21mu \bigcirc} {\overline {{{{\left| {p({\mathbf{r}})} \right|}}^{2}}} } dS > 0\).

Note also that, after we discretize the equation and introduce the grid of sources, expression (8) takes the following form: \(\overline {{{p}_{i}}p_{j}^{ * }} = \sum\nolimits_{k = 1}^{{{N}_{s}}} {{{G}_{{ik}}}G_{{jk}}^{ * }\overline {{{{\left| {{{a}_{k}}} \right|}}^{2}}} } \) \( = \sum\nolimits_{k = 1}^{{{N}_{s}}} {\overline {{{{\left| {{{a}_{k}}} \right|}}^{2}}} {{{\left( {{{q}_{k}}q_{k}^{H}} \right)}}_{{ij}}}} \).

Note that the correlation method allows scaling with respect to independent microphone measurements [12]. For this purpose, it suffices to write the blocks corresponding to different measurements in forming matrices \(\widetilde C\) and \((G \otimes G^{ * })\) of the system one below another:

$${\text{ }}\left( {\begin{array}{*{20}{c}} {{{{\widetilde C}}^{1}}} \\ \hline {{{{\widetilde C}}^{2}}} \\ \hline \vdots \\ \hline {{{{\widetilde C}}^{{{{N}_{{{\text{pos}}}}}}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{{{(G \otimes G^{ * })}}^{1}}} \\ \hline {{{{(G \otimes G^{ * })}}^{2}}} \\ \hline \vdots \\ \hline {{{{(G \otimes G*)}}^{{{{N}_{{{\text{pos}}}}}}}}} \end{array}} \right)\tilde {A}.$$

For the method with uncorrelated sources, we have

$${\text{ }}\left( {\begin{array}{*{20}{c}} {\widetilde C_{{{\text{reduce}}}}^{1}} \\ \hline {\widetilde C_{{{\text{reduce}}}}^{2}} \\ \hline \vdots \\ \hline {\widetilde C_{{{\text{reduce}}}}^{{{{N}_{{{\text{pos}}}}}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {(G \otimes G^{ * })_{{{\text{reduce}}}}^{1}} \\ \hline {(G \otimes G^{ * })_{{{\text{reduce}}}}^{2}} \\ \hline \vdots \\ \hline {(G \otimes G^{ * })_{{{\text{reduce}}}}^{{{{N}_{{{\text{pos}}}}}}}} \end{array}} \right){{\tilde {A}}_{{{\text{uncorrelated}}}}}.$$

It is also worth noting that the problem formulation with uncorrelated sources is well-posed in the cases in which the sources are correlated, but the scale of their correlation is less than the resolution capability of the microphone array; in this case, the sound field cannot be discriminated from the field of delta-correlated sources with the same direction as an individual coherent structure. In particular, this condition is met for compact (the characteristic scale is less than the wavelength) sound sources. At low Mach numbers (\({{{\text{M}}}^{2}} \ll 1\), the characteristic length of the studied wave is far larger than the size of the vortex zone and the arising sources can be regarded as compact. Thus, at low Mach numbers, the subsonic aerodynamic sources of noise can be correctly described within the proposed paradigm.

METHOD FOR NUMERICAL DETERMINATION OF SOURCE AMPLITUDES

To simplify the notation, in this section, we introduce denotations not related with other parts of the paper.

For linear systems of the form \(Ax = b\), taking into account the fact that the right-hand side is assumed to be given with errors, because it has been measured experimentally, it makes sense to find the solution as the minimum of the expression

$${{\left\| {Ax - b} \right\|}_{2}}\xrightarrow[x]{}\min .$$
(10)

The solution to minimization problem (10) is equivalent to the solution to the linear system

$${{A}^{H}}Ax = {{A}^{H}}b.$$
(11)

The solution to system (11) can be sought by the conjugate gradient method [13]:

$$\frac{1}{2}\left( {{{c}^{H}}x + {{x}^{H}}c} \right) + \frac{1}{2}{{x}^{H}}Gx\xrightarrow[x]{}\min ,$$
(12)

where \(G = {{A}^{H}}A\) and \(c = {{A}^{H}}b\).

The iteration scheme of the solution is as follows:

$$\begin{gathered} {{p}_{k}} = - {{g}_{k}} + {{\beta }_{k}}{{p}_{{k - 1}}},\,\,\,\,{{\alpha }_{k}} = \frac{{\left\| {{{g}_{k}}} \right\|_{2}^{2}}}{{p_{k}^{H}G{{p}_{k}}}}, \\ {{x}_{{k + 1}}} = {{x}_{k}} + {{\alpha }_{k}}{{p}_{k}},\,\,\,\,{{g}_{k}} = c + G{{x}_{k}},\,\,\,\,{{\beta }_{k}} = \frac{{\left\| {{{g}_{k}}} \right\|_{2}^{2}}}{{\left\| {{{g}_{{k - 1}}}} \right\|_{2}^{2}}}. \\ \end{gathered} $$
(13)

Here, for components \({{x}_{{k + 1}}}\), we apply an additional procedure related with nonnegativity of the mean squares of amplitudes. If negative components \({{x}_{{k + 1}}}\) arise during iterations, then their sign is changed to the opposite one:

$${\text{if }}x_{{k + 1}}^{i} < 0 \to x_{{k + 1}}^{i} = - x_{{k + 1}}^{i},\,\,\,\,i = \overline {1,{{N}_{s}}} .$$
(14)

As the starting point of the algorithm, we chose the values

$${{\beta }_{0}} = 0,\,\,\,\,{{g}_{0}} = c.$$

METHOD VERIFICATION

We verified the developed method numerically using model examples of identification of mutually uncorrelated sources; for this purpose, we introduced both a monopole and dipole into our model. The position of sources was modeled in a plane parallel to the plane of the microphone array. The coordinates of the microphones used to recognize the sources are depicted in Fig. 2. This microphone array is a virtual image of the real microphone array available in the Anechoic Room AK-2 of the Central Aerohydrodynamic Institute.

Fig. 2.
figure 2

Coordinates of microphones of a virtual planar microphone array.

Full size image

The sources located in different nodes of the source grid are assumed to be uncorrelated. Moreover, in each node there are three types of sources that are also mutually uncorrelated:, with a monopole and two dipole components oriented in the plane of sources:

$$\begin{gathered} G_{{kl}}^{1} = \frac{{{{e}^{{ik\left| {r_{k}^{m} - r_{l}^{s}} \right|}}}}}{{\left| {r_{k}^{m} - r_{l}^{s}} \right|}}, \\ G_{{kl}}^{2} = \frac{{{{{(r_{k}^{m} - r_{l}^{s})}}_{x}}{{e}^{{ik\left| {r_{k}^{m} - r_{l}^{s}} \right|}}}}}{{{{{\left| {r_{k}^{m} - r_{l}^{s}} \right|}}^{2}}}}\left( {ik - \frac{1}{{\left| {r_{k}^{m} - r_{l}^{s}} \right|}}} \right), \\ G_{{kl}}^{3} = \frac{{{{{(r_{k}^{m} - r_{l}^{s})}}_{y}}{{e}^{{ik\left| {r_{k}^{m} - r_{l}^{s}} \right|}}}}}{{{{{\left| {r_{k}^{m} - r_{l}^{s}} \right|}}^{2}}}}\left( {ik - \frac{1}{{\left| {r_{k}^{m} - r_{l}^{s}} \right|}}} \right), \\ \end{gathered} $$
(15)

where \(G_{{kl}}^{1}\) is a monopole, \(G_{{kl}}^{2}\) is an x-dipole, \(G_{{kl}}^{3}\) is a y-dipole (it is assumed that the sources are located in the plane \(XY\)), \(r_{k}^{m}\) is the coordinate of the \(k\)th microphone, and \(r_{l}^{s}\) is the coordinate of the \(l\)th node of the grid of sources.

In generating spectral matrix \({{C}_{{ij}}} = \overline {{{p}_{i}}p_{j}^{ * }} \), the property of source uncorrelation was simulated by means of multiple realizations with different random phases between all the sources. In particular, we considered 150 realizations in the provided examples.

The plane of sources was situated at a distance of 1 m from the plane of the microphone array.

We present the maps of source localization at a frequency of 1000 Hz. We simulated a pair of sources: a monopole and an x-dipole. The monopole was located at the position (–0.25, 0), and the x-dipole was located at the position (0.2, –0.2). We represented three cases: simultaneous modeling of a monopole and dipole (the input data are acoustic fields from an uncorrelated monopole and dipole), separate modeling of monopole (the input data are the acoustic field of a monopole), and separate modeling of dipole (the input data are the acoustic field of a dipole).

The results of source localization accurately correspond to the numerically given values. For a dipole component (as we see in Figs. 3a and 3b), the dynamic range for this configuration was \( \sim 6\) dB. When we remove the x-dipole from simulation, the corresponding level of intensity of the field of x-dipoles reduced by \( \sim 9\) dB (Figs. 3a, 3d, 3g). When the monopole was removed, the level of intensity of the field of monopoles decreased by \( \sim 12\) dB (Figs. 3c, 3f, 3i).

Fig. 3.
figure 3

Maps of acoustic-source localization: (a–c) simultaneous modeling of monopole and x-dipole, (d–f) modeling of monopole, (g–i) modeling of x-dipole, (a, d, g) output of x-dipole intensity, (b, e, h) output of y-dipole intensity, and (c, f, i) output of monopole intensity.

Full size image

We also modeled the configuration of sources with the same spatial position, but a different dipole amplitude, which was increased three times.

The method allows correctly recognizing both the monopole and dipole at such ratio of amplitudes. Here, judging by the acoustic map for the y-dipole, the dynamic range is \( \sim 10\) dB relative to the dominating dipole sources.

INVESTIGATION OF METHOD STABILITY

To check the possibility of using our method in a real experiment, we studied its stability. First, we consider the effect of inaccuracy in prescribing wavenumber k = ω/c. For this purpose, as input data, we used an incorrect value of speed of sound in the medium \(c\). The sources were modeled with \(c = 330\) m/s. In the implemented algorithm, we used \(c = 340\) m/s. The configuration of sources was the same as in Fig. 3. Comparison of the results with correct and inaccurate wavenumber values are given in Fig. 5.

Fig. 4.
figure 4

Maps of acoustic-source localization (the amplitude of x-dipole is three times larger than the amplitude of monopole): (a) output of x-dipole intensity, (b) output of y-dipole intensity, and (c) output of monopole intensity.

Full size image
Fig. 5.
figure 5

Effect of inaccuracy in prescribing the wavenumber. We simultaneously modeled monopole and x-dipole: (a–c) wavenumber is given correctly and (d–f) wavenumber is given with a mistake, by varying the speed of sound from 330 to 340 m/s.

Full size image

A moderate variation in wavenumber \(k\) does not lead to a strong distortion of the returned acoustic map. In Fig. 5, we see that the localization and amplitude values of the monopole and dipole sources are almost unchanged. If we judge by the component of the y-dipole, which is absent in modeling the sources, the level of dynamic range decreased by 1 dB.

We also investigated the effect of inaccuracy in prescribing the position of the source plane relative to the microphone array (Fig. 6). For this purpose, we shifted the position of the source localization plane in parallel by 2 cm from the real position. In this case, we considered the configuration of the sources, where the dipole has an amplitude that is three times greater. Thus, the amplitude of the modeled dipole did not disappear at the background of errors. This is related with the fact that, in terms of the structure of dipole orientation, the microphone array occurs in the region of the minimum of its acoustic radiation and the monopole dominates in terms of the level of signals induced at microphones.

The dynamic range decreased from \( \sim 10\) to \( \sim 4\) dB. The method is sufficiently sensitive to the accuracy of prescribing the region of location of acoustic sources in constructing the grid of sources, at least in the considered configuration of the microphone array, types of sources, and their localization. Apparently, the use of a three-dimensional microphone array [9, 12, 14] will allow improving the identification quality and increasing the dynamic range, because it will cover the maximums of the direction of dipole sound sources.

CONCLUSIONS

The method for identifying sound sources based on the correlation analysis of acoustic fields is developed. Under the assumption of uncorrelated sound sources, this approach allows reducing the inverse problem of determining the field of sources by the data of multiple-microphone measurements to a well-posed problem without invoking additional assumptions about the structure of sources. Note that this approach is suitable only in the case of uncorrelated point sources. The results have a general character; therefore, their applicability to aircraft applications and the range of parameters under which this assumption is possible will be studied further.

The developed method was numerically verified using the example of determining the field of sources composed of both monopole and dipole components. As a result of numerical tests, we demonstrated that the method allows correctly determining the amplitudes of monopoles and two components of dipoles, with dipole moments oriented in parallel to the plane of the microphone array. We studied the stability of the method in the case of inaccuracies in prescribing the wavenumber and position of the plane of sources.

Further research will be intended to adapt the developed method to apply it to the noise of the turbulent jet and to determination of spatial distribution of intensity of quadrupole sources according to the Lighthill analogy [15].

Fig. 6.
figure 6

Effect of inaccuracy in prescribing the position of source plane. We simultaneously modeled monopole and x-dipole with an amplitude that is three times larger: (a–c) position of source array corresponds to real position of sources and (d–f) source array is shifted by 2 cm from the real position of sources away from the microphone array.

Full size image