INTRODUCTION

The acousto-optic delay line (AODL) is an effective tool for signal processing in the time domain [1–4]. A smoothly controllable delay of signals over a wide time interval (several tens of microseconds) makes it possible to build high-performance radar simulators based on them [5, 6]. In an AODL, the effective signal processing in the time domain is due to the low speed of propagation of the acoustic wave (slower by a factor of about 105 than the speed of propagation of an electromagnetic wave) in a photoelastic medium (PEM). The elastic wave propagation speed v also predetermines the character and parameters of the acousto-optic interaction, since an elastic wave with the same velocity enters an optical beam with a small diameter \(d\). Under these conditions, the cutoff frequency AODL is defined as

$${{f}_{{{\text{cut}}}}} = {{0.4375} \mathord{\left/ {\vphantom {{0.4375} {\left( {{d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}} \right).}}} \right. \kern-0em} {\left( {{d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}} \right).}}$$

It follows from this expression that in order to increase the cutoff frequency of the AODL, it is necessary to reduce the diameter of the light beam and use a PEM with a high propagation velocity of of the elastic wave. In any case, the limit of practical application of an AODL is set by the relation \({d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}\). This indicates that the pulse width \({{\tau }_{i}}\) at the AODL input must be longer than the time of crossing the optical beam by the acoustic wave [7]; i.e., the condition \({{\tau }_{i}} > {d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}\) must be satisfied. However, research has shown that in the case of \({{\tau }_{i}} < {d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}\) at the output of AODL, a certain response is also formed, which is characterized by properties suitable for solving both the main problem related to signal processing in the time domain, and a number of other particular and specific practical problems. In other words, AODL can also be used above the cutoff frequency.

The aim of this study is to study the parameters of the AODL response to a rectangular input action with duration \({{\tau }_{i}} < {d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}\), derive the calculated relations for their analysis, and develop recommendations for the application of the features of the photoelastic interaction at frequencies above the boundary.

DESIGN AND OPERATING PRINCIPLE OF AN AODL

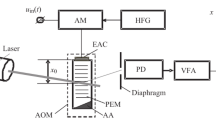
Structurally, an AODL is implemented based on an acousto-optic modulator (AOM), which consists of a PEM and an electroacoustic transducer (EAT) attached to its end [8].

The AOM bandwidth is 40–60% of its central frequency, which is selected in the range from tens of megahertz to gigahertz units. As a rule, the processed signal \({{u}_{{{\text{in}}}}}(t)\) has a low-frequency spectrum. An amplitude modulator (AM) and a high frequency generator (HFG) are used to transfer the signal to the AOM operating frequency range. The AM output is connected to the EAT terminals, which excites an elastic wave in the PEM that travels to the acoustic absorber (AA). When the laser beam falls into the PEM aperture (in this case, at the Bragg angle, at which only one diffraction order appears), a photoelastic effect is observed, i.e., part of the light is deflected (Fig. 1). The spatial position and intensity of the deflected light are determined by the parameters of the RF electrical signal supplied to the EAT terminals [9]. The deflected light beam is recorded by a photomultiplier tube (PMT).

Fig. 1.
figure 1

AODL scheme.

Full size image

The cross section of the interaction of an elastic wave packet with duration \({{\tau }_{i}}\) and width H, and an optical beam with a circular cross-sectional diameter d in the x0z plane for the case \({{\tau }_{i}} < {d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}\) is shown in Fig. 2.

Fig. 2.
figure 2

Geometry of acousto-optic interaction in the plane perpendicular to the direction of propagation of the laser beam (τi < d/v).

Full size image

THEORETICAL STUDY

The traditional AODL algorithm a priori assumes that useful information is contained in the electrical signal that is fed to the EAT terminals. In the context of the purpose of this study, it is more convenient to assume that useful information is contained in the light beam that falls into the PEM aperture. Note that such a formulation of the problem can take place when it is necessary to extract information from an optical signal. Under these conditions, if we assume that the coordinate system moves along the x axis at speed v, the AODL can be viewed as a linear stationary system with a rectangular impulse response of duration \({{\tau }_{i}}\). Such a sequence of physical processes allows us to assume that the optical beam enters the considered linear stationary system with velocity v. In this case, that part of the optical beam which is within the cross-sectional area participates in the acousto-optical interaction:

$${{S}_{1}}(x) = \int\limits_x^{x + v{{\tau }_{i}}} {H{\kern 1pt} '(x)dx} {\text{ at }}{{x}_{0}} \leqslant x \leqslant {{x}_{0}} + d + v{{\tau }_{i}},$$
(1)

where the length of the line of interaction of the leading front of the elastic wave packet with the laser beam in the x0z plane (see Fig. 2)

$$\begin{gathered} H{\kern 1pt} '(x) = 2\sqrt {d(x - {{x}_{0}}) - {{{(x - {{x}_{0}})}}^{2}}} {\text{ }} \\ {\text{at }}{{x}_{0}} \leqslant x \leqslant {{x}_{0}} + d. \\ \end{gathered} $$
(2)

Here x is the current coordinate; and \({{x}_{0}}\) is the distance from the EAT to the acousto-optic interaction point (see Fig. 1).

Under these conditions, the power of the deflected light beam is determined by the formula

$${{P}_{1}}(x) = {{{{S}_{1}}(x)\eta {{P}_{0}}} \mathord{\left/ {\vphantom {{{{S}_{1}}(x)\eta {{P}_{0}}} {{{S}_{0}}}}} \right. \kern-0em} {{{S}_{0}}}},$$
(3)

where \(\eta \) is the diffraction efficiency of the AOM; and \({{P}_{0}}\) and \({{S}_{0}}\) are the power and cross-sectional area of the light beam incident into the AOM aperture, respectively.

It should be noted that the diffraction efficiency of the AOM at the constant power of the input electrical signal is a constant value for the selected specific AODL design [10].

The deflected light beam hits the PMT photosensitive surface through a hole in the diaphragm. The PMT output current is determined according to the laws of general physics by the formula

$${{i}_{{{\text{out}}}}}(x) = {{Ge\eta {\kern 1pt} '{{P}_{1}}(x)} \mathord{\left/ {\vphantom {{Ge\eta {\kern 1pt} '{{P}_{1}}(x)} {(h\nu )}}} \right. \kern-0em} {(h\nu )}},$$
(4)

where \(G\) is the gain of the PMT; \(e = 1.6\,\, \times \,\,{{10}^{{ - 19}}}\,{\text{Kl}}\) is the proton charge; \(\eta {\kern 1pt} '\) is the quantum yield of the photocathode (the average number of electrons emitted by the photocathode when one photon is incident on it); \(h = 6.63\,\, \times \,\,{{10}^{{ - 34}}}\,{\text{J s}}\) is Planck’s constant; and \(\nu \) is the frequency of light. The number of photons that fall on the PMT’s photosensitive surface per second is determined by the \({{{{P}_{1}}(x)} \mathord{\left/ {\vphantom {{{{P}_{1}}(x)} {(h\nu )}}} \right. \kern-0em} {(h\nu )}}\) ratio.

The PMT output current generates the following voltage on the load with resistance \({{R}_{{\text{l}}}}\):

$${{u}_{{{\text{out}}}}}(x) = {{R}_{{\text{l}}}}{{i}_{{{\text{out}}}}}(x).$$
(5)

Substituting formulas (1)–(4) into (5), we obtain the following equation for the output voltage of the AODL:

$$\begin{gathered} {{u}_{{{\text{out}}}}}(x) = \frac{{2{{R}_{{\text{l}}}}Ge\eta {\kern 1pt} '\eta {{P}_{0}}}}{{h\nu {{S}_{0}}}}\int\limits_x^{x + v{{\tau }_{i}}} {\sqrt {d(x - {{x}_{0}}) - {{{(x - {{x}_{0}})}}^{2}}} dx} \\ {\text{at }}{{x}_{0}} \leqslant x \leqslant {{x}_{0}} + d + v{{\tau }_{i}}. \\ \end{gathered} $$
(6)

Given that the current coordinate \(x\) is related to the current time t by the equality \(x = vt\), we rewrite Eq. (6) in the following form:

$$\begin{gathered} {{u}_{{{\text{out}}}}}(x) = c\int\limits_t^{t + {{\tau }_{i}}} {\sqrt {{{\tau }_{0}}(t - \tau ) - {{{(t - \tau )}}^{2}}} dt} \\ {\text{at }}\tau \leqslant t \leqslant \tau + {{\tau }_{0}} + {{\tau }_{i}}, \\ \end{gathered} $$
(7)

where \(c = {{2{{R}_{{\text{l}}}}Ge\eta {\kern 1pt} '\eta {{P}_{0}}{{v}^{2}}} \mathord{\left/ {\vphantom {{2{{R}_{{\text{l}}}}Ge\eta {\kern 1pt} '\eta {{P}_{0}}{{v}^{2}}} {(h\nu {{S}_{0}})}}} \right. \kern-0em} {(h\nu {{S}_{0}})}}\) is a constant factor; \({{\tau }_{0}} = {d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}\) is the time constant AODL; and \(\tau = {{{{x}_{0}}} \mathord{\left/ {\vphantom {{{{x}_{0}}} v}} \right. \kern-0em} v}\) is the delay due to the travel time of the elastic wave packet from EAT to the point of the acousto-optic interaction.

When calculating the integral in Eq. (7), it is necessary to distinguish three areas. The first region is characterized by the entry of an elastic wave packet into the aperture of the optical beam. In this case, the output voltage is calculated by the formula

$$\begin{gathered} {{u}_{{{\text{out}}.1}}}(t) = c\int\limits_\tau ^t {\sqrt {{{\tau }_{0}}(t - \tau ) - {{{(t - \tau )}}^{2}}} dt} \\ {\text{at }}\tau \leqslant t \leqslant \tau + {{\tau }_{i}}. \\ \end{gathered} $$
(8)

The second region is characterized by the process of propagation of an elastic wave packet in the aperture of the optical beam. Here the calculation is carried out according to the following equation:

$$\begin{gathered} {{u}_{{{\text{out}}.2}}}(t) = c\int\limits_{t - {{\tau }_{i}}}^t {\sqrt {{{\tau }_{0}}(t - \tau ) - {{{(t - \tau )}}^{2}}} dt} \\ {\text{at }}\tau + {{\tau }_{i}} \leqslant t \leqslant \tau + {{\tau }_{0}}. \\ \end{gathered} $$
(9)

The third region is characterized by the process of the exit of an elastic wave packet from the aperture of the optical beam. Here the calculation is carried out by the expression

$$\begin{gathered} {{u}_{{{\text{out}}.3}}}(t) = c\left[ {\int\limits_\tau ^{\tau + {{\tau }_{0}}} {\sqrt {{{\tau }_{0}}(t - \tau ) - {{{(t - \tau )}}^{2}}} dt} } \right. \\ \left. { - \int\limits_\tau ^{t - {{\tau }_{i}}} {\sqrt {{{\tau }_{0}}(t - \tau ) - {{{(t - \tau )}}^{2}}} dt} } \right], \\ \end{gathered} $$
(10)

at \(\tau + {{\tau }_{0}} \leqslant t \leqslant \tau + {{\tau }_{0}} + {{\tau }_{i}}\).

The output voltage is the sum of three terms determined by Eqs. (8)–(10):

$$\begin{gathered} {{u}_{{{\text{out}}}}}(t) = {{u}_{{{\text{out}}.1}}}(t) + {{u}_{{{\text{out}}.2}}}(t) + {{u}_{{{\text{out}}.3}}}(t){\text{ }} \\ {\text{at }}\tau \leqslant t \leqslant \tau + {{\tau }_{0}} + {{\tau }_{i}}. \\ \end{gathered} $$
(11)

NUMERICAL SIMULATION

The AODL response is simulated with parameters \(d = 1.6\,\,{\text{mm}}\), \(v = 3.63\,\,{{{\text{km}}} \mathord{\left/ {\vphantom {{{\text{km}}} {\text{s}}}} \right. \kern-0em} {\text{s}}}\), and \(\tau = 0.6\,\,\mu {\text{s}}\) on a rectangular input action with duration \({{\tau }_{i}} = 0.1\,\,\mu {\text{s}}\) and \({{\tau }_{i}} = 0.3\,\,\mu {\text{s}}\). Obviously, in both cases, the condition \({{\tau }_{i}} < {d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}\); i.e., photoelastic interaction occurs in the forbidden region.

The formula for modeling the output voltage PMT in the Mathcad environment is obtained from the joint analysis of Eqs. (8)–(11) in the following form:

$$\begin{gathered} {{u}_{{{\text{out}}}}}(t) = {{u}_{{{\text{out}}.1}}}(t)\left[ {\Phi (t - \tau ) - \Phi (t - \tau - {{\tau }_{i}})} \right] \\ + \,\,{{u}_{{{\text{out}}.2}}}(t)\left[ {\Phi (t - \tau - {{\tau }_{i}}) - \Phi (t - \tau - {{\tau }_{0}})} \right] \\ + \,\,{{u}_{{{\text{out}}.3}}}(t)\left[ {\Phi (t - \tau - {{\tau }_{0}}) - \Phi (t - \tau - {{\tau }_{0}} - {{\tau }_{i}})} \right] \\ {\text{at }}\tau \leqslant t \leqslant \tau + {{\tau }_{0}} + {{\tau }_{i}}, \\ \end{gathered} $$
(12)

where \(\Phi (t)\) is the Heaviside unit step function.

Normalized graphs of voltages at the output of AODL constructed according to formula (12) for cases \({{\tau }_{i}} = 0.1\,\,\mu {\text{s}}\) and \({{\tau }_{i}} = 0.3\,\,\mu {\text{s}}\) are shown in Fig. 3, from which it is easy to determine that in both cases the pulse width at the AODL output (measured at 0.5 of the maximum value) is approximately 0.4 μs. Thus, in the forbidden region (beyond the boundary frequency), the duration of the output pulse does not depend on the duration of the input pulse \({{\tau }_{i}}\) and is determined by the relationship \({d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}\). In this case, the duration of the acousto-optical interaction (measured at the zero level) depends on the duration of the input pulse \({{\tau }_{i}}\) and is determined by the sum \({d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v} + {{\tau }_{i}}\). The spread between the magnitude \({d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}\) and the duration of the output pulse is due to the fact that due to the circular cross section of the light, the area of the acousto-optical interaction in the plane perpendicular to the direction of propagation of the laser beam changes nonlinearly. It is obvious that the shorter the duration of the input pulse \({{\tau }_{i}}\) the closer the shape of the graph is to the configuration of the cross section of the laser beam. In the case under consideration, a uniform distribution of the power flux density in the cross section of the laser beam is assumed. For the limiting case, i.e., when \({{\tau }_{i}} \to 0\), formula (11) has the following form:

$$\mathop {{\text{Lim}}}\limits_{{{\tau }_{i}} \to 0} \left[ {{{u}_{{{\text{out}}}}}(t)} \right] = {{u}_{{{\text{out}}.2}}}(t){\text{ at }}\tau \leqslant t \leqslant \tau + {{\tau }_{0}} + {{\tau }_{i}}.$$
Fig. 3.
figure 3

Normalized voltage graph at the AODL output.

Full size image

EXPERIMENTAL

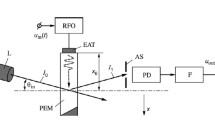
The established provisions and the results of numerical simulation are verified experimentally. The layout diagram for experimental research and the measuring equipment used are shown in Fig. 4. Here, a semiconductor laser L is used as a light source. The laser beam falls into the AOM aperture at the Bragg angle.

Fig. 4.
figure 4

Layout diagram for experimental research.

Full size image

The rectangular pulse from the the G5-54 generator modulates the oscillation of the G4-107 high-frequency generator, which operates in the external pulse modulation mode, and synchronizes the MSO4052 oscilloscope. The oscillation frequency of the G4-107 generator is chosen equal to the central frequency of the AOM, which in this case is 80 MHz. The deflected light falls through the slit in the diaphragm D onto the light-sensitive surface of the PMT-114.

Oscillograms of pulses at the input and output of the AODL with parameters \(d = 1.6\,\,{\text{mm}}\), \(v = 3.63\,\,{{{\text{km}}} \mathord{\left/ {\vphantom {{{\text{km}}} {\text{s}}}} \right. \kern-0em} {\text{s}}}\), and \(\tau = 0.6\,\,\mu {\text{s}}\) are shown in Fig. 5. The duration of the input pulse, which is determined from the oscillogram at the level of 0.5 of the maximum value, \({{\tau }_{i}} \approx 0.3\,\,\mu {\text{s}}\); i.e., the condition \({{\tau }_{i}} < {d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}\) is satisfied.

Fig. 5.
figure 5

Oscillograms of pulses at the input (2) and at the output (1) of the AODL with parameters v = 3630 m/s, d = 1.6 mm, τ = 0.6 μs.

Full size image

The parameters of the oscillogram of the output pulse (Fig. 5, curve 1) agree closely with the parameters of the calculated graph in Fig. 3 for the case \({{\tau }_{i}} = 0.3\,\,\mu {\text{s}}\). The duration of the output pulse is approximately 0.4 μs. This corresponds to the established statement and proves that under the condition \({{\tau }_{i}} < {d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}\) the duration of the output pulse is independent of the duration of the input pulse (Fig. 5, curve 2). The duration of the acousto-optical interaction determined from the calculated graph and from the oscillogram is approximately 0.74 μs. In Fig. 5, curve 1, this parameter is determined, taking into account the inertia of the measuring instruments. All this proves that under the condition \({{\tau }_{i}} < {d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}\) the duration of the output pulse is determined by the time taken to cross the optical beam by the elastic wave packet, i.e., by the ratio \({d \mathord{\left/ {\vphantom {d v}} \right. \kern-0em} v}\).

Thus, the experimental data confirm the established regularities and coincide with the results of the numerical analysis.

CONCLUSIONS

In the known applications of an AODL, the limit of the practical realization of its capabilities is determined by the time taken to cross the optical beam by an elastic wave. The limiting parameters of the AODL, namely, its cutoff frequency and, accordingly, the permissible minimum duration of the input pulse, are estimated by this parameter.

It was found that the AODL is characterized by some extraordinary capabilities, which, in addition to its direct functional purpose, can also be used to solve other radio engineering problems, for example, to extract information about the energy-geometric characteristics of quasi-coherent light.