1 INTRODUCTION

At present, considerable attention in the field of micro- and nanoelectronics is being paid to the development of device structures based on 2D materials, especially graphene [1, 2]. Graphene has a number of unique properties for creating a new element base for micro- and nanoelectronics: highly mobile charge carriers, ambipolarity, and high level of conductivity. Thus, field-effect graphene transistors (FGTs) can be used in high-speed electronics, especially in analog and RF devices [3].

A significant difference in the physics of the functioning of field-effect transistors based on semiconductor materials and FGTs necessitated the creation of models specifically for FGT. The fundamental difference is clearly manifested in the transfer characteristics of FGTs, which have a hole conduction region to the left of the Dirac point and electronic conductivity to the right of the Dirac point. In recent years, numerous works have been devoted to FGT models and obtaining experimental samples of these devices, which is reflected in the review on compact FGT models [4].

Such models can be developed based on a diffusion-drift model with various modifications [5–7]; the kinetic Boltzmann equation with modifications [8, 9]; Green’s functions [10]; and Landauer’s formulas [11]. Models can also be designed for single-layer [7, 11], two-layer [12, 13], and multilayer [14] FGTs. In [15], a model is described for the proposed construction of a graphene-based tunneling transistor.

In this paper, we present a brief description of the proposed simplified combined self-consistent model of a field-effect transistor based on single-layer graphene (Fig. 1), as well as the simulation results obtained with its use. The influence of the dielectrics of FGT gates on their current–voltage (I–V) characteristics is investigated.

Fig. 1.
figure 1

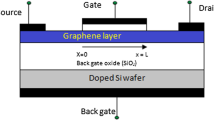
Cross section of a dual-gate FGT based on single-layer graphene: S, source; G, upper gate; BG, back (lower) gate; D, drain; (1) substrate; (2) the dielectric of the lower gate; (3) dielectric of the upper gate; (4) metal of the upper gate; (5) metal of the lower gate; (6) source and drain metal; (7) graphene.

Full size image

2 MODEL

The proposed model is based on the equations of the quantum diffusion-drift model [16, 17] and belongs to the class of combined models according to the classification [17, 18]. In the model, the electrostatic potential of the channel and the quantum capacity are calculated self-consistently using the iterative method. When implementing the algorithm of the transfer characteristics, the dichotomy method was used to take into account the drain resistance Rd and source Rs. A detailed description of the model is given in articles [19–21]. Therefore, here we give the main relations of the model, which is a combination of physical-topological and electrical models.

At the first stage, the capacities of the upper \({{C}_{{gt}}}\) and lower \({{C}_{{gb}}}\) gates are calculated. Next, the electrostatic potential is self-consistently calculated \(V\) using the iterative method according to the following formulas [22, 23]:

$$V = \frac{{{{C}_{{gt}}}\left( {{{V}_{{tg}}} - {{V}_{{tg0}}} - {{V}_{a}}} \right) + {{C}_{{gb}}}\left( {{{V}_{{beff}}} - {{V}_{a}}} \right)}}{{{{C}_{{gt}}} + {{C}_{{gb}}} + \alpha {{C}_{q}}}},$$
(1)
$$\alpha = \frac{1}{2}\left( {\frac{1}{{1 + \frac{{{{q}^{2}}{{V}^{2}}}}{{{{{(kT\ln (4))}}^{2}}}}}} + 1} \right),$$
(2)
$${{C}_{q}} = \frac{{2{{q}^{3}}}}{{\pi {{{(\hbar {{V}_{F}})}}^{2}}}}\left| V \right|,$$
(3)

where \({{C}_{{gt}}}\) and \({{C}_{{gb}}}\) are capacitances of the upper and lower gates; \(\alpha \) is the capacity factor (\(\alpha \) = 0.5 at \(q\left| V \right| \gg kT\)); \(q\) is the electron charge; \(\hbar \) is Planck’s constant divided by \(2\pi \); \({{V}_{F}}\) is the Fermi velocity equal to \({{V}_{F}}\)= 106 m/s; \({{V}_{{tg}}}\) is the voltage at the upper gate; \({{V}_{{beff}}}\) is the effective voltage at the lower gate; \({{V}_{{tg0}}}\) is the Dirac voltage for the upper gate; \(V\) is the electrostatic potential of the channel; \({{V}_{a}}\) ranges from 0 to \({{V}_{{ch}}}\); \({{V}_{{ch}}}\) is the full voltage drop in the channel; \(L\) is the channel length; \(k\) is the Boltzmann constant; and \(T\) is the ambient temperature.

The system of equations (1)–(3) is solved iteratively until the correction of the electrostatic potential in the channel reaches the given value.

At the second stage, based on the electrostatic potential found in the channel, the total charge density of the graphene sheet \(Q\) is calculated according to [24]:

$$Q = \frac{{q\pi {{{\left( {kT} \right)}}^{2}}}}{{3{{{(\hbar {{V}_{F}})}}^{2}}}} + \frac{{{{q}^{3}}{{V}^{2}} + q{{\Delta }^{2}}}}{{\pi {{{(\hbar {{V}_{F}})}}^{2}}}}.$$
(4)

Next, the effective mobility of the charge carriers in graphene \(\mu \) is calculated taking into account the mobility of the electrons and holes [23]:

$$\mu = \left( {\frac{{14({{\mu }_{p}} - {{\mu }_{n}})\left( {\frac{{\pi {{{\left( {kT} \right)}}^{2}}}}{{3{{{(\hbar {{V}_{F}})}}^{2}}}} + \frac{{{{q}^{2}}}}{{\pi {{{(\hbar {{V}_{F}})}}^{2}}}}{{V}^{2}}} \right)V}}{{\left( {\frac{{\pi {{{\left( {kT} \right)}}^{2}}}}{{3{{{(\hbar {{V}_{F}})}}^{2}}}} + \frac{{{{q}^{2}}{{V}^{2}} + {{\Delta }^{2}}}}{{\pi {{{(\hbar {{V}_{F}})}}^{2}}}}} \right)\sqrt {1 + \frac{{{{q}^{2}}}}{{{{{(kT\ln (4))}}^{2}}}}{{V}^{2}}} }} + h} \right)\frac{m}{{m + {{V}^{2}}}},$$
(5)

where \({{\mu }_{p}}\) and \({{\mu }_{n}}\) are the mobility of the electrons and holes, respectively, \(\Delta \) is the inhomogeneity of the electrostatic potential, and \(h\) and \(m\) are matching parameters of the model.

The drain current is determined by the formula obtained from the quantum diffusion-drift model [25, 26]:

$${{I}_{d}} = \frac{{W\int\limits_0^{{{V}_{{ch}}}} {\mu QdV} }}{{L + \left| {\int\limits_0^{{{V}_{{ch}}}} {\frac{\mu }{{{{V}_{{sat}}}}}dV} } \right|}},$$
(6)

where \(W\) is the channel width and \({{V}_{{sat}}}\) is the saturation velocity.

The saturation velocity is calculated based on the model [24] and allows us to take into account the scattering by the optical phonons:

$${{V}_{{sat}}} = \left\{ \begin{gathered} \frac{{2{{V}_{F}}}}{\pi },\,\,{\text{if}}\,\,\left| {{{Q}_{{net}}}} \right| \leqslant q\left| {{{\rho }_{{crit}}}} \right| \hfill \\ \frac{{2q\Omega }}{{{{\pi }^{2}}\hbar {{V}_{F}}\left| {{{Q}_{{net}}}} \right|}}\sqrt {\frac{{\pi {{{(\hbar {{V}_{F}})}}^{2}}\left| {{{Q}_{{net}}}} \right|}}{q} - {{{\left( {\frac{{\hbar \Omega }}{2}} \right)}}^{2}}} ,\,\,\,\,{\text{if}}\,\,\,\left| {{{Q}_{{net}}}} \right| > q\left| {{{\rho }_{{crit}}}} \right|, \hfill \\ \end{gathered} \right.$$
(7)
$${{\rho }_{{crit}}} = \frac{1}{{2\pi }}\left( {\frac{\Omega }{{{{V}_{F}}}}} \right),$$

where \({{\rho }_{{crit}}}\) is the critical density of the charge carriers, \({{Q}_{{net}}}\) is the charge density of the carriers in the channel (\({{Q}_{{net}}} = \left| {\alpha {{C}_{q}}V} \right|\)), and \(\hbar \Omega \) is the effective energy of the optical phonons.

Note that if we do not take into account quantum phenomena and voltage drops at the drain and source regions, then in this case \({{V}_{{ch}}} = {{V}_{d}}\) (\({{V}_{d}}\) is the voltage applied to the drain with respect to the source), and relation (6) leads to the traditional diffusion-drift model used by many authors (sometimes with modifications and corrections [5–7, 22, 27]) when calculating the drain current of the FGTs.

At the final stage of obtaining the transfer I–V characteristic of the FGT, in order to take into account the voltage drops across the resistances of the drain regions \({{R}_{d}}\) and source regions \({{R}_{s}}\), it is necessary to recalculate the drain current \({{I}_{d}}\) at a fixed drain voltage \({{V}_{d}}\) by applying the optimization method. We used the dichotomy method [19–21]. This method has been successfully used to solve much more complex problems of the multidimensional numerical simulation of fragments of silicon VLSI [28, 29]. The current does not need to be recalculated only in the special case when the resistance of the drain region \({{R}_{d}}\) and source region \({{R}_{s}}\) is not taken into account, i.e., \({{R}_{d}} = {{R}_{s}} = 0\) [26, 30].

3 RESULTS AND DISCUSSION

The developed models and the corresponding software were tested on the example of calculating the transfer and output I–V characteristics of a dual-gate FGT [31] with Al2O3 as the upper gate dielectric at room temperature. As follows from Figs. 2 and 3, good agreement of the simulation results with the experimental data was achieved for both transfer characteristicsFootnote 1 and for the output characteristics of the FGT. This increases our confidence in the validity of the theoretical results presented below.

Fig. 2.
figure 2

Transfer I–V characteristic of a dual-gate FGT with the following dielectrics of the upper gate: (1) HfO2; (2) SiC; (3) Al2O3; (4) h-BN; (5) SiO2; (6) experimental data for FGT with Al2O3 dielectric.

Full size image
Fig. 3.
figure 3

Output I–V characteristic of a dual-gate FGT with the following dielectrics of the upper gate: (1) HfO2; (2) SiC; (3) Al2O3; (4) h-BN; (5) SiO2; (6) experimental data for FGT with Al2O3 dielectric.

Full size image

Figures 2 and 3 show the calculations for five different FGTs with the same geometric dimensions but which differ in the dielectric material of the upper gate. Apart from Al2O3 [32], the other dielectrics were chosen according to the principle used in the experimental research works on graphene transistors: silicon dioxide SiO2 [33], silicon carbide SiC [34], hafnium dioxide HfO2 [11, 35–37], and hexagonal boron nitride h-BN [38]. The substrate material for all the investigated FGTs was doped silicon and the dielectric material of the lower gate was silicon dioxide.

Figure 2 shows the results of calculating the transfer I–V characteristic of the investigated devices at room temperature and voltage at the drain, Vd = 0.6 V; Fig. 3 shows the output characteristics of the FGT at a fixed voltage at the upper gate of Vtgt = –1 V. Figure 3 shows how significant the influence of the upper gate of the FGT is on the I–V characteristic of the dielectric material. Curve 1 corresponds to an FGT with an upper gate dielectric of HfO2; curve 2, SiC; curve 3, Al2O3; curve 4, h-BN; and curve 5, SiO2.

Table 1 shows the results of calculating the current swing for the transfer characteristics of all five FGTs. If we follow the principles of operation of field-effect transistors, then the best devices are those with the largest current swing, that is, the ratio of the maximum and minimum drain currents of the device.

Table 1.   Parameters of transfer characteristics of FGTs
Full size table

Let us consider the region of hole conduction to the left of the Dirac point. With a smaller swing at the –1 V point and with a larger swing at –2 V relative to the Dirac point, the best FGTs are from HfO2 (Table 1), followed by FGTs from SiC, Al2O3, h-BN, SiO2, respectively.

The influence of dielectrics on the I–V characteristics of the FGT is due to their different dielectric constant, which affects the gate capacitance, and the different energies of the optical phonons for these materials with a graphene layer located on them. The corresponding data for the calculations were taken from [39] for dielectrics of SiO2, HfO2, SiC, and h‑BN, as well as from [23, 40] for Al2O3 (Table 2). It is interesting to note that in the region of electronic conductivity to the right of the Dirac point, the values of the range Idmax/Idmin are close to similar values in the region of hole conductivity, which is related to a certain symmetry of the transfer I–V characteristics with respect to the Dirac point.

Table 2.   Dielectric constants and scattering parameters for graphene on various substrates
Full size table

The asymmetry of the behavior of the transfer characteristics in the regions of electron and hole conduction is mainly due to the contact resistance. Figure 2 shows the shift of the Dirac point to the right, if we trace the behavior of curves 1–5 (Fig. 2), for the corresponding FGTs with different dielectrics of the upper gate. This is due to a decrease in the dielectric constant of the dielectrics of the upper gate, from the highest for HfO2 with \(\varepsilon = \) 22.0 to the lowest for SiO2 with \(\varepsilon = \) 3.9 (Table 2).

For a better understanding of the influence of the upper and lower dielectrics on the transfer characteristics of an FGT, let us consider the effect separately of each of the parameters: the dielectric constant of the lower gate, the dielectric constant of the upper gate, scattering by optical phonons, and the thicknesses of the upper and lower gates.

Figure 4 illustrates the influence \(\varepsilon \) of the dielectric of the lower gate on the transfer I–V characteristic of the dual-gate FGT. Figure 4 clearly shows the shift of the Dirac point to the region of higher voltages as \(\varepsilon \) of the dielectric of the lower gate increases.

Fig. 4.
figure 4

Transfer I–V characteristic of a dual-gate FGT at different \({{\varepsilon }_{{}}}\) of dielectric of lower gate: (1) SiO2 (\({{\varepsilon }_{b}}\) = 3.9); (2) h-BN (\({{\varepsilon }_{b}}\)= 5.09); (3) Al2O3 (\({{\varepsilon }_{b}}\) = 8.9); (4) SiC (\({{\varepsilon }_{b}}\) = 9.7); (5) HfO2 (\({{\varepsilon }_{b}}\) = 22.0).

Full size image

For comparison, consider the change in the dielectric constant of the upper gate (Fig. 5). An inverse relationship is observed here, i.e., the greater the dielectric constant the more the Dirac point shifts to the region of lower voltages; while the drain current and the ratio of the maximum current to the minimum current increase. The change in current is much more noticeable.

Fig. 5.
figure 5

Transfer I–V characteristic of a dual-gate FGT at different \({{\varepsilon }_{{}}}\) of dielectric of upper gate: (1) SiO2 (\({{\varepsilon }_{t}}\) = 3.9); (2) h-BN (\({{\varepsilon }_{t}}\) = 5.09); (3) Al2O3 (\({{\varepsilon }_{t}}\) = 8.9); (4) SiC (\({{\varepsilon }_{t}}\) = 9.7); (5) HfO2 (\({{\varepsilon }_{t}}\) = 22.0).

Full size image

Thus, it can be seen that the influence of the dielectric of the upper gate on the drain current is stronger than that of the lower gate, which is explained by the significant difference in the gate capacitances, which are calculated based on \(\varepsilon \) of the dielectric of the corresponding gate.

Consider an example of an FGT with an upper gate dielectric of HfO2 and a lower gate dielectric of SiO2. In this case, the capacity per unit area of the upper gate is 1.2 × 10–2 F/m2 and the lower one is 1.5 × 10–4 F/m2. The difference in these capacitances by two orders of magnitude affects the electrostatic potential in the channel calculated later (see formula (1)), and, consequently, the drain current, i.e., the I–V characteristic of the device. The displacement of the graphs to the left or to the right is also determined by the value of the electrostatic potential, and, therefore, the corresponding parameters (apart from the dielectric constants, the value of the applied displacement to the upper and lower gates, as well as the Dirac voltage for the upper gate, is important). As the studies have shown, with the other parameters unchanged, if \(\varepsilon \) of the dielectric of the upper gate is greater than \(\varepsilon \) of the dielectric of the lower gate, the shift of the Dirac point on the transfer I–V characteristics will be to the right, and the greater this difference, the stronger the bias (Fig. 5).

Figure 6 shows that a change in the scattering by the optical phonons has an insignificant effect on the characteristics of the devices. The values of the scattering by the optical phonons for these calculations were taken from various sources: curve 1 corresponds to \(\hbar {{\omega }_{{opt}}}\) = 55.0 meV [40]; and curve 2, to \(\hbar {{\omega }_{{opt}}}\) = 75.0 meV [24]. Value \(\hbar {{\omega }_{{opt}}}\) = 85.0 meV (curve 3) is given for comparison. As follows from the calculations performed, the effect of this parameter should be considered together with the dielectric constant of the material.

Fig. 6.
figure 6

Transfer I–V characteristic of a dual-gate FGT with different values of scattering by optical phonons: (1) \(\hbar {{\omega }_{{opt}}}\) = 55 meV [41]; (2) \(\hbar {{\omega }_{{opt}}}\) = 75 meV [24]; (3) \(\hbar {{\omega }_{{opt}}}\) = 85 meV.

Full size image

The effect of the optical phonons for various materials of the lower gate is illustrated in Figs. 7 and 8. In these examples, the upper gate is made of Al2O3, (\({{\varepsilon }_{t}}\) = 8.9), and the dielectrics of the lower gates change. The effect of the change caused by the scattering by the optical phonons for various materials was estimated with respect to the corresponding Al2O3, i.e., \(\hbar {{\omega }_{{opt}}}\) = 55.0 meV. For each of the materials, this effect is insignificant (for example, for curves 3 and 4 in Fig. 7, corresponding to the lower dielectric of SiO2). This is explained by the small difference between the scattering by the optical phonons for SiO2 (\(\hbar {{\omega }_{{opt}}}\) = 58.9 meV) and for Al2O3 (\(\hbar {{\omega }_{{opt}}}\) = 55.0 meV). The biggest difference is for curves 1 and 2 in Fig. 7, corresponding to the lower dielectric of HfO2. Note that since \(\hbar {{\omega }_{{opt}}}\) = 21.6 meV for HfО2 is less than that from Al2O3 with \(\hbar {{\omega }_{{opt}}}\) = 55.0 meV, the drain currents correspondingly decrease, in contrast to all other cases (curves 1 and 2 in Fig. 8 for SiC, curves 3 and 4 in Fig. 8 for h-BN, curves 2 and 3 in Fig. 7 for SiO2), for which the drain current for the corresponding material increases.

Fig. 7.
figure 7

Transfer I–V characteristic of a dual-gate FGT with scattering on optical phonons corresponding to different dielectrics of the lower gate: (1) \({{\varepsilon }_{b}}\) = 22.0 (HfО2), \(\hbar {{\omega }_{{opt}}}\)= 55 meV; (2) \({{\varepsilon }_{b}}\) = 22.0 (HfО2), \(\hbar {{\omega }_{{opt}}}\)= 21.6 meV; (3) \({{\varepsilon }_{b}}\) = 3.9 (SiO2), \(\hbar {{\omega }_{{opt}}}\)= 58.9 meV; (4) \({{\varepsilon }_{b}}\) = 3.9 (SiO2), \(\hbar {{\omega }_{{opt}}}\)= 55.0 meV.

Full size image
Fig. 8.
figure 8

Transfer I–V characteristic of a dual-gate FGT with scattering on optical phonons corresponding to different dielectrics of the lower gate: (1) \({{\varepsilon }_{b}}\) = 9.7 (SiC), \(\hbar {{\omega }_{{opt}}}\) = 116.0 meV; (2) \({{\varepsilon }_{b}}\) = 9.7 (SiC), \(\hbar {{\omega }_{{opt}}}\)= 55.0 meV; (3) \({{\varepsilon }_{b}}\) = 5.09 (h-BN), \(\hbar {{\omega }_{{opt}}}\)= 101.7 meV; (4) \({{\varepsilon }_{b}}\) = 5.09 (h-BN), \(\hbar {{\omega }_{{opt}}}\)= 55.0 meV.

Full size image

The effect of the thickness of the upper gate’s dielectric on the transfer characteristics of an FGT with an Al2O3 dielectric was also studied. Its thickness varied from 15 to 30 nm with a step of 5 nm, which corresponds to curves 1 to 4 in Fig. 9. As follows from Fig. 9, the Dirac point with an increase in the dielectric thickness shifts to the region of higher voltages at the upper gate, and the current swing decreases. This is due to the fact that the increase in the thickness of the dielectric leads to a decrease in the capacitance of the upper gate, and, as a consequence, to a change in the electrostatic potential in the FGT channel, which in turn affects the I–V characteristic of the device.

Fig. 9.
figure 9

Transfer I–V characteristic of a dual-gate FGT with different thicknesses of the dielectric of the upper gate: (1) dtg = 15 nm; (2) dtg = 20 nm; (3) dtg = 25 nm; (4) dtg = 30 nm.

Full size image

In Fig. 10 the transfer I–V characteristic of a dual-gate FGT with different thicknesses of the dielectric of the lower gate are shown. The dielectric thickness was varied from 300 to 420 nm with a step of 60 nm, which corresponds to curves 1 to 3. It was found that the effect of the thickness of the lower gate on the I–V characteristic is insignificant. It can be seen that with an increase in the thickness of the dielectric, the Dirac point shifts slightly to the region of lower voltage values at the upper gate, and the current swing in the characteristics remains practically unchanged. This is due to the fact that the capacitance per unit area of the lower gate is much less than the corresponding capacitance of the upper gate, and, therefore, has a smaller effect on the change in the electrostatic potential in the channel, and as a result, on the transfer I–V characteristic of the FGT.

Fig. 10.
figure 10

Transfer I–V characteristic of a dual-gate FGT with different thicknesses of the lower gate dielectric: (1) dbg = 300 nm; (2) dbg = 360 nm; (3) dbg = 420 nm.

Full size image

4 CONCLUSIONS

Using the proposed simplified combined self-consistent model of an FGT, a significant effect of the dielectric material of the upper gate on the output and transfer current-voltage characteristics of field-effect transistors based on single-layer graphene is shown. The calculated characteristics of five FGTs, which differ in terms of the dielectric of the upper gate, are analyzed. It was found that the highest ratio of the maximum drain current to the minimum drain current on the I–V characteristic is possessed by an FGT from HfO2, and the smallest ration, to an FGT from SiO2. Overall, the results for all five FGTs lead us to conclude that the performance of the investigated transistors is acceptable.

It has been established that a change in the thickness of the dielectric of the lower gate (of up to tens of nanometers) insignificantly affects the I–V characteristic of the FGT but even a small change in the thickness of the dielectric of the upper gate (of several nanometers) leads to visible changes in the characteristics of the device, which will obviously be important in the manufacturing of devices.

The programs implementing the model are included in the NANODEV system for modeling nanoelectronic devices [41, 42], which has been developed at Belarusian State University of Informatics and Radioelectronics (BSUIR) since 1995.