INTRODUCTION

Multiferroics attract much attention of researchers from scientific and practical points of view, since these materials have both magnetic and ferroelectric properties under the same external conditions [1]. This is often due to the existence of a magnetoelectric effect in such materials [2]. In multiferroics, antiferromagnetism and ferroelectricity most often coexist, and ferroelectric ferromagnets are quite rare materials. The appearance of electric polarization induced by a magnetic field can be explained on the basis of the three most popular microscopic mechanisms: the mechanism related to the antisymmetric Dzyaloshinskii–Moriya interaction [3, 4], magnetostriction [5], and spin-dependent metal–ligand hybridization. We focus our attention on the Dzyaloshinskii–Moriya interaction, since it causes noncollinear spin ordering. Inhomogeneous magnetic ordering, in turn, can lead to polarization [6, 7].

The magnetism of small-sized particles has attracted much attention in recent years due to the possibility of their practical applications [8, 9]. “Single-domain” particles are potential candidates for use as memory elements in high-density hard disk storage. However, as the particle size increases, their magnetic state changes to a vortex or multidomain state [10–14]. Discussion of magnetic phase transitions in small particles has become particularly popular [12]. There are materials with different types of structural, magnetic, orbital, and charge ordering, and among them the most interesting are manganites, high-temperature cuprate superconductors, and multiferroics. Phase separation in these materials is often accompanied by a nonuniform charge distribution [5, 6, 15, 16].

This paper examines the relationship between magnetism and ferroelectricity in submicrometer ferromagnetic particles near the temperature of the magnetic phase transition from the paramagnetic to the ferromagnetic state. The purpose of the work is to determine the spatial distribution of inhomogeneous magnetization caused by size effects, and to study the properties of spatially inhomogeneous polarization arising as a result of spatial inhomogeneity of magnetization in spherical particles. The objectives of the work also include the determination of the region of existence of such inhomogeneous states in the coordinates linear particle size–temperature and the consideration of changes in local electric polarization in a small external magnetic field. All calculations were carried out within the framework of a phenomenological approach.

RESULTS AND DISCUSSION

We consider a three-dimensional spherical ferromagnetic particle placed in a paraelectric medium. The harmonic part of the Landau–Ginzburg–Devonshire free energy [7] near a second-order phase transition has the form

$$F = \int {dV~\left( {\frac{A}{2}{{{\vec {m}}}^{2}} + \frac{g}{2}{{{\left( {\nabla \vec {m}} \right)}}^{2}}} \right) + {{F}_{{{\text{EM}}}}}} ,$$
(1)

where \(\vec {m}\left( {\vec {r}} \right)\) is the local magnetization; V is the volume of the spherical particle; \(\nabla \) is the vector differential operator; the term \(A\) determines the exchange interaction: \(A = A{\kern 1pt} '\left( {T - {{T}_{{\text{c}}}}} \right)\), and \({{T}_{{\text{c}}}}\) is the temperature of magnetic phase transition of a bulk sample; \(g\) is the gradient term obtained previously [7]. The inhomogeneous magnetoelectric effect contributes to the free energy \({{F}_{{{\text{EM}}}}}\) of the crystal, which has the following form for a bulk crystal [7]:

$${{F}_{{{\text{EM}}}}} = \smallint dV~\gamma \vec {E} \cdot \left( {\vec {m} \cdot \left( {\nabla \cdot \vec {m}} \right) - \left( {\vec {m} \cdot \nabla } \right) \cdot \vec {m}} \right).$$
(2)

Here, \(\vec {E}\) is the electric field strength and \(\gamma \) is the magnetoelectric coupling constant. We assume that the contribution to energy by the magnetoelectric effect is small; i.e., the constant \(\gamma \) is small. Then, when determining magnetization, we can first neglect \({{F}_{{{\text{EM}}}}}\). The effective magnetic field \({{H}^{{{\text{eff}}}}}\left( {\vec {r},~t} \right)\) is defined as the variation of the free energy change \(F - {{F}_{{{\text{EM}}}}}\) with magnetic moment \(\vec {m}\):

$${{\vec {H}}^{{{\text{eff}}}}}\left( {\vec {r},~t} \right) = {{ - {{\delta }}\left( {F - {{F}_{{{\text{EM}}}}}} \right)} \mathord{\left/ {\vphantom {{ - {{\delta }}\left( {F - {{F}_{{{\text{EM}}}}}} \right)} {{{\delta }}\vec {m}}}} \right. \kern-0em} {{{\delta }}\vec {m}}}{{\;}}.$$
(3)

Since we are considering a spherical particle, we change to a spherical coordinate system \(r\), \(\theta \), and \(\varphi \). The origin of the spherical coordinate system is placed at the center of the particle. The angle \(\theta \) (\(0 \leqslant \theta \leqslant \pi \)) is counted from the z axis; the angle \(\varphi \) (\(0 \leqslant \varphi < 2\varphi \)), from the x axis. To determine the spatial distribution of the magnetic moment vector\({{\;}}\vec {m}\) and, subsequently, the electric polarization vector \(\vec {p}\), let us consider the variation \(\delta {\text{(}}F - {{F}_{{{\text{EM}}}}})\) with \(\delta {{m}_{\varphi }}\). If this variation is zero, then the magnetization is a solution to the equation

$$\begin{gathered} A{{m}_{\varphi }} + \frac{g}{{{{r}^{2}}{{{\left( {\sin \left( \theta \right)} \right)}}^{2}}}}{{m}_{\varphi }} - \frac{g}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}\left( {{{r}^{2}}\frac{{\partial {{m}_{\varphi }}}}{{\partial r}}} \right) \\ - \,\,\frac{g}{{{{r}^{2}}\sin \left( \theta \right)}}\frac{\partial }{{\partial \theta }}\left( {\sin \left( \theta \right)\frac{{\partial {{m}_{\varphi }}}}{{\partial \theta }}} \right) = 0. \\ \end{gathered} $$
(4)

The magnetization distribution that occurs when stability is lost with respect to the vortex inhomogeneous state has the form

$${{m}_{r}} = 0,\,\,\,\,{{m}_{\theta }} = 0,\,\,\,\,{{m}_{\varphi }}\left( {r,~\varphi } \right) = C{{j}_{1}}\left( {{{p_{1}^{1}r} \mathord{\left/ {\vphantom {{p_{1}^{1}r} R}} \right. \kern-0em} R}} \right)\sin \left( \theta \right),$$
(5)

where \({{m}_{r}}\), \({{m}_{\theta }}\), and \({{m}_{\varphi }}\left( {r,~{{\theta }}} \right)\) are the projections of the local magnetization vector on the axes of the spherical coordinate system; \({{j}_{{\text{1}}}}\left( x \right)\) is the spherical Bessel function of the first order; R is the particle radius; \(p_{n}^{1}\) is the nth root of the equation \(j_{1}^{'}\left( x \right) = 0\); and \(C = {\text{const}}\). Loss of stability with respect to vortex formation corresponds to the minimum value of the constant \(p_{1}^{1} \approx 2.1\). The function \({{j}_{1}}\left( {{{p_{1}^{1}r} \mathord{\left/ {\vphantom {{p_{1}^{1}r} R}} \right. \kern-0em} R}} \right)\) is an increasing function of \(r\) at \(0 \leqslant r \leqslant R\) and has a maximum at \(r = R\).

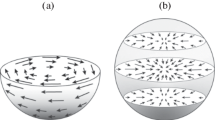
Figure 1a presents the distribution of magnetization on the surface of the spherical particle, i.e., at points \(r = R\), at \(C > 0\). The arrows show the local magnetization vectors. Near a second-order phase transition to a ferromagnetic state, for particles of submicrometer size, an approximation can be used in which the value of local magnetization depends on the distance to the center of the particle. One of the solutions to Eq. (4) is the vortex state (5).

Fig. 1.
figure 1

Magnetization distributions on the surface of a spherical particle immediately after a phase transition from a paramagnetic to a ferromagnetic state: (a) in the case where \({{m}_{r}} = {{m}_{\theta }} = 0\) and \({{m}_{\varphi }} = {{m}_{\varphi }}\left( {r,~\varphi } \right)\) (expression (5)) at \(r = R\), where \(R\) is the particle radius; and (b) in the case where \({{m}_{r}} = {{m}_{\varphi }} = 0\) and \({{m}_{\theta }} = {{m}_{\theta }}\left( {r,~\varphi } \right)\) (Eq. (7)) at \(r = R\). The arrows show the magnitudes and directions of the local magnetization vectors on the particle surface.

Full size image

Let’s consider the second case, where \({{m}_{r}} = {{m}_{\varphi }} = 0\) and \({{m}_{\theta }} = {{m}_{\theta }}\left( {r,\theta } \right)\). To determine the spatial distribution of the magnetic moment vector\({{\;}}\vec {m}\), let us consider the variation \(\delta {\text{(}}F - {{F}_{{{\text{EM}}}}})\) with \(\delta {{m}_{{{\theta }}}}\). If this variation is zero, then the magnetization is a solution to the equation

$$\begin{gathered} A{{m}_{\theta }} + \frac{g}{{{{r}^{2}}{{{\left( {\sin \left( \theta \right)} \right)}}^{2}}}}{{m}_{\theta }} \\ - \,\,\frac{g}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}\left( {{{r}^{2}}\frac{{\partial {{m}_{{{\theta }}}}}}{{\partial r}}} \right) - \frac{g}{{{{r}^{2}}{\kern 1pt} \sin \left( \theta \right)}}\frac{\partial }{{\partial \theta }}\left( {\sin \left( \theta \right)\frac{{\partial {{m}_{\theta }}}}{{\partial \theta }}} \right) = 0, \\ \end{gathered} $$
(6)

which is similar to Eq. (4).

The solution to Eq. (6) has the form

$${{m}_{\theta }}\left( {r,~\theta } \right) = {{C}_{2}}{{j}_{1}}\left( {{{p_{1}^{1}r} \mathord{\left/ {\vphantom {{p_{1}^{1}r} R}} \right. \kern-0em} R}} \right)\sin \left( \theta \right),$$
(7)

where \({{C}_{2}} = {\text{const}}\).

Figure 1b shows the distribution of magnetization on the surface of the spherical particle in this case (at \({{C}_{2}} > 0\)). Unlike the first case shown in Fig. 1a, the total magnetization of the particle is not zero. It is important to note that the distribution of magnetization inside the particle is inhomogeneous, just like on the surface, and depends on the distance from the center of the particle. The magnetization modulus, as can be seen from expressions (5) and (7), increases monotonically in the direction from the center of the particle to the surface.

For cubic crystals, the acceptable form of magnetically induced electric polarization [7, 15] is the equation that is obtained by differentiating the magnetoelectric contribution to free energy (2):

$$\vec {p} = \gamma \left( {\left( {\vec {m} \cdot \nabla } \right) \cdot \vec {m} - \vec {m} \cdot \left( {\nabla \cdot \vec {m}} \right)} \right).$$
(8)

This equation was obtained for the case where the electric polarization is determined by the Dzyaloshinskii–Moriya interaction [3, 4]. For a 3D-vortex state in the bulk of the ball at \({{m}_{r}} = {{m}_{\theta }} = 0\) and \({{m}_{\varphi }} = {{m}_{\varphi }}\left( {r,~{{\varphi }}} \right)\) (see expression (5)), the polarization has the form

$$\begin{gathered} \vec {p}\left( {r,\theta } \right) = - \gamma {{C}^{2}}\frac{{j_{1}^{2}\left( {{{p_{1}^{1}r} \mathord{\left/ {\vphantom {{p_{1}^{1}r} R}} \right. \kern-0em} R}} \right)\sin \left( \theta \right)}}{r} \\ \times \,\,\left( {\sin \left( \theta \right){{{\vec {e}}}_{r}} + \cos \left( \theta \right){{{\vec {e}}}_{\theta }}} \right). \\ \end{gathered} $$
(9)

Here, \({{\vec {e}}_{r}}\) and \({{\vec {e}}_{\theta }}\) are the unit vectors of the spherical coordinate system. If we rewrite this expression in the Cartesian coordinate system, it becomes clear that the local polarization at each point of the spherical particle lies in the xy plane, i.e., has no projections onto the z axis. Figure 2 shows the distribution of local polarization in the xy plane passing through the center of the particle. The polarization vectors, which are shown by arrows, lie in the xy plane of the Cartesian coordinate system and directed towards the z axis. The length of the arrows at different points of the section is proportional to the magnitude of the polarization vector at these points. From Eq. (9), it is clear that, since the local polarization is proportional to the square of the constant C, it does not depend on the direction in which the magnetization “spins”, but depends only on the direction of the axis of the vortex state.

Fig. 2.
figure 2

Distribution of local electric polarization \(\vec {p}\left( {{{{\vec {m}}}_{0}}} \right)\) inside a spherical particle in the plane z = 0 passing through the center of the particle, which was calculated using Eq. (9).

Full size image

In the second case of magnetization distribution, i.e., at \({{m}_{r}} = {{m}_{\varphi }} = 0\) and \({{m}_{\theta }} = {{m}_{\theta }}\left( {r,\theta } \right) = \) \({{C}_{2}}{{j}_{1}}\left( {{{p_{1}^{1}r} \mathord{\left/ {\vphantom {{p_{1}^{1}r} R}} \right. \kern-0em} R}} \right)\sin \left( \theta \right)\) (see Fig. 1b), substitution of magnetization into Eq. (8) gives the same Eq. (9) as in the case of magnetization in the form of a vortex. Thus, the polarization in the particle (see Fig. 2) has the same form for two different magnetization distributions.

The vortex magnetization distribution discussed above in this article leads to a polarization distribution for which the total polarization of the particle is zero. But at such a magnetization distribution, the total polarization may differ from zero in an external magnetic field.

Ferromagnetic particles can also be “single-domain” uniformly magnetized formations. Homogeneous states of ferromagnetic particles arise if the magnetic energy of a uniformly magnetized particle is less than the energy of a similar particle for which there is a nonuniform distribution of magnetization in the bulk of the particle. The first energy has the order \(A{{M}^{2}}V\); and the second, \(g{{M}^{2}}V{\text{/}}{{l}^{2}}\). Here, \(M\) is the total magnetization of the particle, \(V\) is its volume, l is the linear particle size, and \(A\) and \(g\) are parameters of Eq. (1) for free energy. Then the size of single-domain particles has a value equal in order of magnitude to \({{R}_{{\text{c}}}} \sim {{\left( {g{\text{/}}A} \right)}^{{1{\text{/}}2}}}\) [17]. If, in a zero external magnetic field, a spherical particle is uniformly magnetized, then, inside it, there is constant magnetic field \({{\vec {h}}_{{\text{s}}}} = - {{\left[ {{{\mu }_{0}}\left( {\mu + 2} \right)} \right]}^{{ - 1}}}\vec {M}\), and the stability of the state with uniform magnetization is lost at \(A = - {{\left[ {{{\mu }_{0}}\left( {\mu + 2} \right)} \right]}^{{ - 1}}}\). In this expression, \(\mu \) is the magnetic permeability of the ferromagnet and \({{\mu }_{0}}\) is the magnetic permeability of vacuum.

The expression \(A = - {{\left[ {{{\mu }_{0}}\left( {\mu + 2} \right)} \right]}^{{ - 1}}}\) determines the critical temperature TCS = TC – ΔTS, where \({{\Delta }}{{T}_{{\text{S}}}} = {{\left[ {A{\kern 1pt} '{{\mu }_{0}}\left( {\mu + 2} \right)} \right]}^{{ - 1}}}\). Above the temperature TCS, the homogeneous state becomes unstable with respect to the emergence of an inhomogeneous state, since the energy of the inhomogeneous state becomes less than the energy of the homogeneous one. Therefore, for the critical radius, we have \(R = {{R}_{{\text{c}}}} = p_{1}^{1}{{\left( {g{{\mu }_{0}}} \right)}^{{1{\text{/}}2}}}{{\left( {\mu + 2} \right)}^{{1{\text{/}}2}}}\), wherein \({{R}_{{\text{c}}}}\) is on the order of 10–20 nm [9].

The vortex state under discussion exists in the temperature range above TCS and below TCV and corresponds to the minimum free energy of the system; therefore, this state is stable (Fig. 3). The upper limit temperature TCV of the existence of an inhomogeneous vortex state can be determined from the equality \(A = - g{{\left( {{{p_{n}^{1}} \mathord{\left/ {\vphantom {{p_{n}^{1}} R}} \right. \kern-0em} R}} \right)}^{2}}\) at n = 1. This temperature is TCV = TC – ΔTV, where \({{\Delta }}{{T}_{V}} = 4.4{\kern 1pt} \log {{\left[ {A{\kern 1pt} '{{R}^{2}}} \right]}^{{ - 1}}}\). Since the value \(g{\text{/}}A{\kern 1pt} '\) is quite small (\(g{\text{/}}A{\kern 1pt} '\) ≈ 5 × 10–16 m2 K), then TCV ∼ TC. For example, ΔTV ≈ 0.05 K at R ≈ 100 nm; that is, the upper limit of the region of existence of inhomogeneous states is near TC. Therefore, the temperature interval of the region of existence of the vortex state is on the order of ΔTS. According to our estimates, ΔTS is a few kelvins. Above TCV, the uniform paramagnetic state is the ground state, and below TCS the ground state is the uniform magnetic state.

Fig. 3.
figure 3

Phase diagram of the existence of an inhomogeneous vortex magnetic state and an inhomogeneous polar state of spherical nanoparticles in coordinates particle radius \(R\)–temperature \(T\). The region of the inhomogeneous vortex state is shaded. \({{T}_{{\text{C}}}}\) is the Curie temperature of the magnetic phase transition of the bulk material, and \({{R}_{{\text{c}}}}\) is the critical radius. At \(R < {{R}_{{\text{c}}}}\), the spherical particle is uniformly magnetized. TCS = TC – ΔTS and TCV = TC – ΔTV are the temperature boundaries of the region of inhomogeneous vortex state. At T > TCS, the homogeneous magnetic state becomes unstable with respect to the appearance of an inhomogeneous state (see text), since the energy of the inhomogeneous state becomes less than the energy of the homogeneous state.

Full size image

Let us consider what happens if the magnetization changes when an external magnetic field is applied, and how the polarization changes in this case. Let us place the particle in weak constant external magnetic field \(\vec {H}\). Then \(\widehat {\vec {m}} = {{\vec {m}}_{0}} + {{\delta }}\vec {m}\), where \({{\vec {m}}_{0}}\) is the magnetization of the particle in the absence of a magnetic field, and \(\delta \vec {m} = \chi \vec {H}\) (\(\chi \) is the magnetic susceptibility, \(\chi \) = const) is an addition to magnetization that occurs under the action of the magnetic field. Then \(\vec {p} = \vec {p}\left( {\widehat {\vec {m}}} \right) = \vec {p}\left( {{{{\vec {m}}}_{0}}} \right) + {{\Delta }}\vec {p}\), where \(\vec {p}\left( {\widehat {\vec {m}}} \right)\) and \(\vec {p}\left( {{{{\vec {m}}}_{0}}} \right)\) have the form of Eq. (9). For the additional polarization, we obtain the equation

$$\Delta \vec {p} = \gamma \chi \left( {\left( {\vec {H} \cdot \nabla } \right) \cdot {{{\vec {m}}}_{0}} - \vec {H} \cdot \left( {\nabla \cdot {{{\vec {m}}}_{0}}} \right)} \right).$$
(10)

Let the magnetization be defined in spherical coordinate system \({{\vec {m}}_{0}} = {{\vec {m}}_{0}}\left( {r,~\theta ,\varphi } \right)\). Let us initially consider the magnetization that has the form of a vortex state (Fig. 1a),

$${{\vec {m}}_{0}} = {{m}_{\varphi }}\left( {r,~\theta } \right) \cdot {{\vec {e}}_{\varphi }},$$
(11)

where \({{m}_{\varphi }}\left( {r,~{{\theta }}} \right)\) is as in expression (5), and \({{m}_{r}} = 0\) and \({{m}_{\theta }} = 0\). Then \(\vec {p}\left( {{{{\vec {m}}}_{0}}} \right)\) has form (9). For a constant magnetic field \(\vec {H}\) in a spherical coordinate system, we have

$$\vec {H} = {{H}_{r}} \cdot {{\vec {e}}_{r}} + {{H}_{\theta }} \cdot {{\vec {e}}_{\theta }} + {{H}_{\varphi }} \cdot {{\vec {e}}_{\varphi }} = {\text{const}},$$
(12)

were \({{H}_{r}}\), \({{H}_{\theta }}\), and \({{H}_{\varphi }}\) are the vector projections of \(\vec {H}\) on the axes of the spherical coordinate system.

For definiteness, we consider only the case where the magnetic field is directed along the z axis of the Cartesian coordinate system, i.e., along the axis of the vortex state (Fig. 1a). In this case, \({{H}_{r}} = H{\kern 1pt} {\text{cos}}\left( {{\theta }} \right)\), \({{H}_{\theta }} = - H{\kern 1pt} {\text{sin}}\left( \theta \right)\), and \({{H}_{\varphi }} = 0\), and as a result for \({{\Delta }}\vec {p}\) we obtain

$${{\Delta }}\vec {p} = \gamma \chi CH\frac{{{\text{sin}}\left( {2\theta } \right)}}{2}\left[ {\frac{{\partial {{j}_{1}}\left( {{{p_{1}^{1}r} \mathord{\left/ {\vphantom {{p_{1}^{1}r} R}} \right. \kern-0em} R}} \right)}}{{\partial r}} - \frac{{{{j}_{1}}\left( {{{p_{1}^{1}r} \mathord{\left/ {\vphantom {{p_{1}^{1}r} R}} \right. \kern-0em} R}} \right)}}{r}} \right] \cdot {{\vec {e}}_{\varphi }}.$$
(13)

This equation is equal to zero at \({{\partial {{j}_{1}}\left( {{{p_{1}^{1}r} \mathord{\left/ {\vphantom {{p_{1}^{1}r} R}} \right. \kern-0em} R}} \right)} \mathord{\left/ {\vphantom {{\partial {{j}_{1}}\left( {{{p_{1}^{1}r} \mathord{\left/ {\vphantom {{p_{1}^{1}r} R}} \right. \kern-0em} R}} \right)} {\partial r}}} \right. \kern-0em} {\partial r}} \approx {{{{j}_{1}}\left( {{{p_{1}^{1}r} \mathord{\left/ {\vphantom {{p_{1}^{1}r} R}} \right. \kern-0em} R}} \right)} \mathord{\left/ {\vphantom {{{{j}_{1}}\left( {{{p_{1}^{1}r} \mathord{\left/ {\vphantom {{p_{1}^{1}r} R}} \right. \kern-0em} R}} \right)} r}} \right. \kern-0em} r}\), i.e., if \(r\) approaches zero, and also at \(\theta = 0,\frac{\pi }{2},\) and \(\pi \). At other \(r\) values, according to Eq. (13), \({{\Delta }}\vec {p}\) is not zero. From Eq. (13), it is clear that, after averaging over the angles θ and φ, the total additional polarization caused by the external magnetic field is zero. That is, in this case, when an external magnetic field is applied, uniform polarization does not occur.

Let us now consider the magnetization in the second case, which has the form \({{\vec {m}}_{0}} = {{m}_{\theta }}\left( {r,\theta } \right){{\vec {e}}_{\theta }}\), \({{m}_{r}} = 0\) and \({{m}_{\varphi }} = 0\), as in Eq. (7) (Fig. 1b). Then, by performing calculations similar to those shown above, for a magnetic field directed along the z axis, we obtain an expression for the contribution to local polarization in the form

(14)

After averaging of this equation over the angles θ and φ, we find that the total additional polarization caused by the external magnetic field is zero in this case as well. However, it should be emphasized that, in these two cases of inhomogeneous magnetic states, under the action of a magnetic field, the local polarization of the particle changes in accordance with Eqs. (13) and (14), which can be observed using local research methods.

CONCLUSIONS

Within the framework of the phenomenological theory, the phase transition from the paramagnetic to the ferromagnetic state in three-dimensional spherical particles of a cubic ferromagnet was studied. It was shown that, for particles with a certain radius, a phase transition to a vortex state is energetically more favorable, and for particles with a size less than a certain critical value, a transition to a uniformly magnetized state is observed. Equations were derived for the inhomogeneous magnetization of spherical particles in two states (vortex and nonvortex) in a zero external magnetic field, taking into account variations of the magnetization amplitude. The inhomogeneous electric polarization related to the inhomogeneous distribution of magnetization in the bulk of these small magnetic particles was calculated. The calculations assumed that the microscopic mechanism of the relationship between polarization and magnetization is due to the Dzyaloshinskii–Moriya interaction. For spherical particles, the region of existence of such inhomogeneous magnetoelectric states was determined in the particle size–temperature coordinates. It was shown that, when a magnetic field is applied along the z axis, the local polarization changes, but the total polarization of the particle remains equal to zero.