1 INTRODUCTION

It is known that the Poisson–Boltsman (PB) equation relates a local electrostatic potential value with a charge density at some point of a system. In spite of numerous drawbacks, the unique properties of this equation (the mathematical simplicity and easiness of modifications) are used when both theoretically considering (as a first approximation) the properties of electrical double layers (EDLs) formed at interfaces [1–7] and analyzing the results of diverse experiments [8–11]. The simplest equation of the PB theory describes a drop of reduced electrostatic potential \(\psi \left( x \right)\) in an electrolyte solution at a boundary with a planar surface:

$$\psi \left( x \right) = {{\psi }_{{{\text{eff}}}}}\exp \left( { - \kappa x} \right).$$
((1))

A surprising property of Eq. (1), which is obtained by solving the linearized PB equation, is the fact that it completely coincides with the solution of the nonlinearized PB equation for large distances from even a strongly charged wall, although it underestimates surface potential \({{\psi }_{{\text{s}}}}\) and the rate of its variations at small distances. (For weakly charged surfaces, \({{\psi }_{{\text{s}}}} = {{\psi }_{{{\text{eff}}}}},\) potential profiles coincide with each other).

Effective surface potential \({{\psi }_{{{\text{eff}}}}}\) in Eq. (1) plays the role of a fitting parameter when smoothing experimental data. For strongly charged particles, the value of |\({{\psi }_{{{\text{eff}}}}}\)| is, as a rule, markedly lower than “real” surface potential |\({{\psi }_{{\text{s}}}}\)|, which is related to the number of ionized groups located on the particle surface. This discrepancy in the values of \({{\psi }_{{\text{s}}}}\) and \({{\psi }_{{{\text{eff}}}}}\) is explained by the fact that, under the action of electrostatic forces, some counterions appear to be so strongly bonded to a particle that the formed particle–counterions “complex” behaves as a single entity possessing a decreased surface charge. From this fact, some researchers have inferred that the properties of strongly charged objects may be described by the linearized PB equation, in which the real surface charge is replaced by an effective one. The sense of this replacement is easily clarified by analyzing the solution of classical PB equation (2) for a positively charged planar surface brought in contact with a 1 : 1 electrolyte [2–7]:

$$\psi \left( x \right) = 2\ln \left[ {\frac{{1 + \exp \left( { - \kappa x} \right){\text{tanh}}\left( {{{{{\psi }_{{\text{s}}}}} \mathord{\left/ {\vphantom {{{{\psi }_{{\text{s}}}}} 4}} \right. \kern-0em} 4}} \right)}}{{1 - \exp \left( { - \kappa x} \right){\text{tanh}}\left( {{{{{\psi }_{{\text{s}}}}} \mathord{\left/ {\vphantom {{{{\psi }_{{\text{s}}}}} 4}} \right. \kern-0em} 4}} \right)}}} \right].$$
((2))

For high surface potentials \(({{\psi }_{{\text{s}}}} \gg 1)\), \({\text{tanh}}\left( {{{{{\psi }_{{\text{s}}}}} \mathord{\left/ {\vphantom {{{{\psi }_{{\text{s}}}}} 4}} \right. \kern-0em} 4}} \right) \to 1{{\;}}\), and expression (2) is simplified:

$$\psi \left( x \right) = 2\ln \left[ {\frac{{1 + \exp \left( { - \kappa x} \right)}}{{1 - \exp \left( { - \kappa x} \right)}}} \right].$$
((3))

At distances from a surface that noticeably exceed the Debye length (x\( \gg \) κ–1), potential \(\psi \left( x \right)~\) becomes completely insensitive to surface potential ψs:

$$\psi \left( x \right) = 4\exp \left( { - \kappa x} \right) = {{\psi }_{{{\text{eff}}}}}\exp \left( { - \kappa x} \right).$$
((4))

Thus, at large distances from a strongly charged planar surface, the electrostatic potential varies according to a law determined by linearized PB equation (1) in which the effective potential takes a value corresponding to the saturation condition \(({{\psi }_{{{\text{eff}}}}} \to \psi _{{{\text{eff}}}}^{{{\text{sat}}}}{{\;}} = 4).\)

Oosawa [12] and Manning [13, 14] were the first to propose the idea of accumulating counterions around strongly charged objects for explaining the behavior of strongly charged linear polyelectrolytes. The essence of this idea consists in the fact that, due to the prevalence of the electrostatic attraction between oppositely charged ions (groups) over the entropic scattering of ions, large amounts of counterions are concentrated (condensed) at a strongly charged surface, thereby substantially decreasing the initial surface charge to some fixed “postcondensation” value. Belloni has shown [15] that simple laws analogous to those reported by Manning may be derived from the PB theory, provided that a surface separating the condensed and free ions has been determined. In the literature, different theoretical [17–21] and experimental [22–26] approaches may be found, which are employed to prove the immobilization of counterions and determine the surface charge values, at which counterions appear to be strongly bonded to a surface.

The aforementioned effects are observed when the surfaces of various objects (spheres, rods, etc.) are strongly charged. The PB theory states that, in such cases, the surface charge neutralization to the postcondensation value becomes possible, provided that the concentration of ions near a surface is markedly higher than the concentration that corresponds to their close packing. The effect of the excluded volume of ions on the electric potential distribution near a charged object remains to be clarified. Great attention is focused on the study of this problem using approaches of different complexities [27–35].

The goal of this work is to study the distributions of the electrostatic potential and the concentration of counterions both in the immediate vicinity of a spherical nanoparticle and at large distances from it under the conditions of a constant surface charge density and a finite size of the ions. Numerical solution has been performed for the modified nonlinear PB equation in which the Boltzmann distribution characteristic of point ions has been replaced by the Langmuir distribution [30–35], which, under the conditions of strongly charged surfaces, prevents the ion concentration from exceeding the saturation concentration that corresponds to the close packing of the ions.

2 MODEL AND CALCULATION METHOD

Let us place a positively charged spherical particle with radius a into an aqueous electrolyte solution. Assume that the charge is uniformly distributed over the particle surface. To compensate for the surface charge under the conditions of thermodynamic equilibrium, counterions (anions) are attracted from the bulk solution to the surface, while coions (cations) are repulsed. The competition between the ion–particle electrostatic interactions, on the one hand, and the concomitant losses of the translational entropy of the ions, on the other hand, promotes a nonuniform distribution of the ions in the proximity of the charged surface. Let us take that, because of the finite size of the ions, their concentration at the surface must not exceed maximum value, which is determined by effective ion radius b: for simple cubic packing, \({{C}^{{{\text{max}}}}} = \frac{1}{{{{{\left( {2b} \right)}}^{3}}{{N}_{{\text{A}}}}}}\) (NA is Avogadro’s number). Then, assume that, under equilibrium conditions, local concentration \({{C}_{i}}\left( r \right)\) of i-type ions in the solution at distance r from the particle center obeys the Langmuir distribution:

$$~~{{C}_{i}}\left( {\mathbf{r}} \right) = \frac{{{{C}_{{0i}}}{\text{exp}}\left[ { - \frac{{{{z}_{i}}e\varphi \left( {\mathbf{r}} \right)}}{{kT}}} \right]}}{{1 + \sum\limits_{i = 1}^n {\frac{{{{C}_{{0i}}}}}{{C_{i}^{{{\text{max}}}}}}} \left\{ {{\text{exp}}\left[ { - \frac{{{{z}_{i}}e\varphi \left( {\mathbf{r}} \right)}}{{kT}}} \right] - 1} \right\}}},$$
((5))

where Сi and С0i are the local concentrations of i-type ions (mol/m3) at a point with electric potential φ(r) and in the bulk solution (φ(∞) = 0), respectively; k is the Boltzmann constant; T is the absolute temperature; e is the elementary charge; and zi is the ion valence. Distribution (5) is transformed into Boltzmann distribution (6) when the effective ion size tends to zero, while maximum concentration Cmax tends to infinity:

$${{C}_{i}} = {{C}_{{0i}}}{{e}^{{{{ - {{z}_{i}}e\varphi } \mathord{\left/ {\vphantom {{ - {{z}_{i}}e\varphi } {kT}}} \right. \kern-0em} {kT}}}}}.$$
((6))

Substituting distribution (5) into the Poisson equation, we obtain the modified Poisson–Boltzmann equation (MPBE), which, for a z1 : z2 electrolyte with volume concentration C0i, takes the following form:

$$\begin{gathered} {{\nabla }^{2}}\varphi = - \frac{{e{{N}_{{\text{A}}}}}}{{\varepsilon {{\varepsilon }_{0}}}} \\ \times \,\,\frac{{\mathop \sum \limits_{i = 1}^2 {{z}_{i}}{{C}_{{0i}}}{\text{exp}}\left[ { - \frac{{{{z}_{i}}e\varphi \left( {\mathbf{r}} \right)}}{{kT}}} \right]}}{{1 + \sum\limits_{i = 1}^2 {\frac{{{{C}_{{0i}}}}}{{C_{i}^{{{\text{max}}}}}}} \left\{ {{\text{exp}}\left[ { - \frac{{{{z}_{i}}e\varphi \left( {\mathbf{r}} \right)}}{{kT}}} \right] - 1} \right\}}}. \\ \end{gathered} $$
((7))

Here, ∇2 is the Laplace operator, ε is the dielectric constant of the solution, and ε0 is the dielectric permittivity of vacuum. The dielectric constant of the solution is assumed to be independent of its concentration and to remain unchanged up to the particle surface. For a symmetric electrolyte consisting of ions with valence z, MPBE (7) may be written in the compact form using the potential and the distance measured in the units of thermal potential φT = kT/e and Debye radius 1/κ, respectively:

$$\psi \left( {\mathbf{r}} \right) = \frac{{ze\varphi \left( {\mathbf{r}} \right)}}{{kT}} = \frac{{z\varphi \left( {\mathbf{r}} \right)}}{{{{\varphi }_{{\text{T}}}}}},$$
((8))
$$\kappa = \sqrt {\frac{{2{{z}^{2}}{{e}^{2}}{{N}_{{\text{A}}}}{{C}_{0}}}}{{kT\varepsilon {{\varepsilon }_{0}}}}} .$$
((9))

Under the condition of equal effective sizes of the counterions and coions, i.e., when their maximum concentrations are the same, \(C_{1}^{{{\text{max}}}} = C_{2}^{{{\text{max}}}} = {{C}_{{{\text{max}}}}},\) the distribution of the electric potential for a 1 : 1 electrolyte (z1 = –z2 = z = 1) in the proximity of a spherical particle is described by the following equation:

$$\frac{{{{d}^{2}}\psi }}{{d{{r}^{2}}}} + \frac{2}{r}\frac{{d\psi }}{{dr}} = \frac{{2{\text{sinh}}\left( \psi \right)}}{{1 + \frac{{2{{C}_{0}}}}{{{{C}_{{\max }}}}}\left[ {{\text{cosh}}\left( \psi \right) - 1} \right]}}.$$
((10))

The traditional PB equation is obtained from the modified one, when the value of parameter Cmax tends to infinity.

We assume that charge density σ remains unchanged on the particle surface, and the electric potential vanishes at a large distance from the particle; i.e., we impose the following boundary conditions:

$$ - {{\left. {\frac{{d\psi }}{{dr}}} \right|}_{{r = \kappa a}}} = \frac{{e\sigma }}{{\varepsilon {{\varepsilon }_{0}}kT\kappa }} = {{\sigma }_{{\text{S}}}},\,\,\,\,\mathop {\lim }\limits_{r \to \infty } \psi \left( r \right) = 0.$$
((11))

Nonlinear differential equation (10) was discretized using finite second-order differences. The nodes were located at equal distances from each other. The numerical solution was performed by the iteration method. The iterations were interrupted when, in successive approximations, the maximum deviation of the calculated potential from the previous one became no larger than 10–9 for all nodes. The steps between the nodes were varied. When analyzing the results obtained , the step was selected in a manner such that potential values ceased to depend on the step magnitude (within the preset error).

Three model parameters were varied in the calculations: (1) particle radius (a = 5, 15, and 40 nm), (2) reduced surface charge density (σs = 1–40), and (3) effective ion size (the sizes of cations and anions were believed to be equal), i.e., the maximum attainable electrolyte concentration that ensured the fulfillment of the conditions of close packing (Cmax= 0.5–10, ∞ mol/L). The electrolyte concentration in the bulk solution far from the particles was maintained unchanged and equal to 0.1 M.

3 RESULTS AND DISCUSSION

The modified PB theory used in this work enables us to analyze the influence of the effective counterion size on variations in the electrostatic potential and the distribution of ions near the surface of a single particle in an electrolyte solution. The data obtained for spherical particles 15 nm in radius will be presented below.

The results of calculating the profiles of the electrostatic potential are presented in Fig. 1 for three different values of the surface charge density (σs = 1, 10, and 40) at counterion sizes corresponding to Cmax ≥ 0.5 M. The data obtained have confirmed the known notion that, for weakly charged particles (in our model, σs = 1 corresponds to this case), the ion size has no effect on the electrostatic potential drop (the profiles in Fig 1a almost coincide with each other), while the drop takes place at distances of, mainly, 1–2 Debye radii (κ–1 ~ 1 nm for a 0.1 M 1 : 1 electrolyte solution). Another situation develops when the surface charge density grows. Now, the solution of Eq. (10) yields profiles (Figs. 1b, 1c, curves 2–6), the values of which are substantially higher than the potentials obtained in terms of the classical PB theory (Figs. 1b, 1c, curves 1). The larger the effective ion size (the lower the maximum attainable electrolyte concentration), the larger the differences between the profiles.

Fig. 1.
figure 1

Variations in the electrostatic potential near a spherical 15-nm particle at surface charge densities σs = (a) 1, (b) 10, and (c) 40. The sizes of electrolyte ions correspond to (a) Cmax ≥ 0.5 М; (b) Cmax = (1) ∞, (2) 3, (3) 1, and (4) 0.5 М; and (c) Cmax = (1) ∞, (2) 10, (3) 3, (4) 1.5, (5) 1, and (6) 0.5 М.

Full size image

The reason for this behavior is quite obvious and associated with the fact that the steric hindrances relevant to the effective sizes of counterions prevent the latter from approaching to a particle surface in amounts sufficient for neutralizing its high charge. In this case, the compensation is realized due to the formation of an extended layer of counterions at the surface. The formation of such a layer is evident from the ion distributions in the proximity of a particle, which are presented in Fig. 2 for σs = 10 and 40. It can be seen in Fig. 2 that, according to the classical PB theory, large amounts of counterions are concentrated in a thin near-surface layer, the thickness of which is close to the Debye radius (~1 nm). Therewith, at ion sizes corresponding to Cmax = 0.5 M, the counterions are concentrated in an extended layer (Fig. 2, curves 4). Its width is estimated to be ~2.5 nm for σs = 10 (Fig. 2a) and ~9 nm for σs = 40 (Fig. 2b). As the maximum attainable concentration increases, the width of the counterion layer decreases (Fig. 2, curves 2–4).

Fig. 2.
figure 2

Variations in the counterion concentration near a spherical 15-nm particle at surface charge densities σs = (a) 10 and (b) 40. Electrolyte ion sizes correspond to Cmax = (1) ∞, (2) 3, (3) 1, and (4) 0.5 М.

Full size image

Thus, two regions with different properties are distinguished in the electrolyte solution located in the proximity of a strongly charged particle surface. A saturated layer of counterions with concentration Cmax is adjacent to the particle. The counterions located in this layer are rather strongly bonded to the particle due to electrostatic interaction. For example, the electrostatic potential at the inflection point of the C(x) profile for Cmax = 0.5 M is, approximately, 1kT, while, at points closer to the particle surface, it noticeably exceeds this value, thereby retaining the anions in the vicinity of the positively charged particles.

Variations in the potential inside of the saturated layer may be estimated by solving Eq. (10), the right-hand side of which comprises constant concentration Cmax that corresponds to the maximum attainable packing of counterions,

$$\frac{{{{d}^{2}}\psi }}{{d{{{\left( {\kappa x} \right)}}^{2}}}} + \frac{2}{{\kappa \left( {a + x} \right)}}\frac{{d\psi }}{{d\left( {\kappa x} \right)}} = \frac{{{{C}_{{\max }}}}}{{{{C}_{0}}}},$$
((12))

with boundary conditions

$$ - {{\left. {\frac{{d\psi }}{{d\left( {\kappa x} \right)}}} \right|}_{{x = 0}}} = {{\sigma }_{{\text{s}}}},\,\,\,\,\psi \left( 0 \right) = {{\psi }_{0}}.$$
((13))

The authors of [30] were the first to obtain the following solution:

$$\psi \left( x \right) = {{\psi }_{0}} - \frac{{{{\sigma }_{{\text{s}}}}\kappa ax}}{{a + x}} + \frac{{{{C}_{{\max }}}\left( {3a + x} \right){{\kappa }^{2}}{{x}^{2}}}}{{6{{C}_{0}}\left( {a + x} \right)}}.$$
((14))

They used Eq. (14) to determine thickness lc of the saturated (condensed) layer of from the position of the minimum in potential ψ(x) as follows:

$${{l}_{{\text{c}}}} = a\left( {\sqrt[3]{{1 + \frac{{3{{C}_{0}}{{\sigma }_{{\text{s}}}}}}{{{{C}_{{\max }}}\kappa a}}}} - 1} \right).$$
((15))

According to Eq. (15), if the particle radius is increased at a fixed surface charge density and concentration corresponding to the close packing of ions \(\left( {\frac{{{{C}_{0}}{{\sigma }_{{\text{s}}}}}}{{{{C}_{{\max }}}\kappa a}} \ll 1} \right),\) he condensed layer thickness ceases to depend on the radius and tends to the thickness of a corresponding layer on a planar surface [32]: \({{l}_{{\text{c}}}} = \frac{{{{C}_{0}}{{\sigma }_{{\text{s}}}}}}{{{{C}_{{{\text{max}}}}}\kappa }}.\) The latter thickness varies in proportion to the surface charge density and the square root of the bulk solution concentration \(\left( {C_{0}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} \right)\) and in inverse proportion to the saturation concentration.

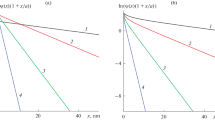
It follows from Fig. 2 that the presence of the condensed layer substantially shifts the diffuse part of the EDL away from the particle surface. Figure 3 presents the electric potential profiles for surface charge densities \({{\sigma }_{{\text{s}}}} = 1{\kern 1pt} - {\kern 1pt} 40\) and maximum attainable concentrations in semilogarithmic coordinates \({\text{ln}}\left[ {\psi \left( x \right)\left( {1 + \frac{x}{a}} \right)} \right] = f\left( x \right)\). The data in Fig. 3 show that, in the chosen coordinate system, a linear dependence is observed for all studied systems in the range, where the potential values are markedly decreased. The slope of the straight lines corresponds to reciprocal Debye length κ with a high accuracy. Thus, there is, indeed, a range of distances, in which the electric potential profile (irrespective of the counterion sizes and the value of the surface charge) acquires the form of

$$\psi \left( x \right) = {{\psi }_{{{\text{eff}}}}}\frac{a}{{a + x}}\exp \left( { - \kappa x} \right),$$
((16))
Fig. 3.
figure 3

Variations in the electrostatic potential near a 15-nm particle at surface charge densities σs = (1) 1, (2) 4, (3) 10, (4) 20, and (5) 40 and electrolyte ion sizes corresponding to Cmax = (a) ∞, (b) 3, and (c) 0.5 М.

Full size image

i.e., is described by the PB theory, with effective surface potential \({{\psi }_{{{\text{eff}}}}}\) differing from the values of real surface potential \({{\psi }_{{\text{s}}}}.\)

As is seen from the data presented in Fig. 3, ion sizes markedly influence the value of factor \({{\psi }_{{{\text{eff}}}}} = \psi \left( {x \to 0} \right).\) According to the data shown in Fig. 3a, we have that, within the framework of the classical PB theory (\({{C}_{{{\text{max}}}}} \to \infty ,\)\(b = 0\)), the potential profiles are almost the same for surface charge densities \({{\sigma }_{{\text{s}}}} \geqslant 20\) and decrease according to law (16) while moving away from the particle at distances larger than the Debye screening length. In this case, we obtain the following for strongly charged particles (irrespective of the value of the surface charge): \(\mathop {\lim }\limits_{x \to 0} \left[ {{\text{ln}}\left( {\psi \left( x \right)} \right)} \right] = 1.376,\) or \({{\psi }_{{{\text{eff}}}}} = 3.958,\) which is close to value \(\psi _{{{\text{eff}}}}^{{{\text{sat}}}} = 4\) for a planar surface (see Eq. (4); Fig. 4, curve 1 ).

Fig. 4.
figure 4

Dependences of the ψeff value in Eq. (16), which describes variations in the electrostatic potential with the distance from the surface of a spherical 15-nm particle, on surface charge density σs for electrolyte ion sizes corresponding to Cmax = (1) ∞, (2) 10, (3), 3 (4) 1, and (5) 0.5 М.

Full size image

At finite sizes of counterions, the modified PB theory shows a completely different situation (Fig. 4). First of all, it should be noted that, at a high surface charge of particles, no saturation is observed for the effective surface potential. As \({{\sigma }_{{\text{s}}}}\) increases, \({{\psi }_{{{\text{eff}}}}}\) also rises, and the lower maximum attainable saturation concentration \({{C}_{{{\text{max}}}}}\), the greater the rise (Fig. 4, curves 2–5). As was noted above and when analyzing the data of Fig. 1a, the actual coincidence of the curves (the closeness of the effective potential values) is observed only for low values of \({{\sigma }_{{\text{s}}}}.\) Moreover, for \({{C}_{{{\text{max}}}}} = \infty \), the saturation potential observed in Fig. 3a is no higher than the real surface electrostatic potential: \({{\psi }_{{{\text{eff}}}}} < {{\psi }_{{\text{s}}}}.\) An analogous behavior is also typical for finite-size ions in the range of maximum attainable electrolyte concentrations (Fig. 3b), however, without \({{\psi }_{{{\text{eff}}}}}\) saturation (at the considered values of the model parameters). At the same time, for , the effective potential is markedly higher than the real one (Fig. 3c) as \({{\sigma }_{{\text{s}}}} \geqslant 10.\) For \({{C}_{{{\text{max}}}}}\) = 1.5 M, the relation \({{\psi }_{{{\text{eff}}}}} > {{\psi }_{{\text{s}}}}\) is fulfilled only at \({{\sigma }_{{\text{s}}}}{{\;}}\) = 40.

Figure 5 shows that, as the ion sizes grow (i.e., their maximum attainable concentration decreases), the effective surface electrostatic potential deviates from the values corresponding to the classical PB model with zero ion sizes. As is seen in Fig. 5, the higher particle surface charge density \({{\sigma }_{{\text{s}}}}\), the greater the deviation.

Fig. 5.
figure 5

Dependences of the ψeff value in Eq. (16), which describes variations in the electrostatic potential with the distance from the surface of a spherical 15-nm particle, on the maximum attainable electrolyte concentration at surface charge densities σs = (1) 1, (2) 4, (3) 10, (4) 20, and (5) 40.

Full size image

4 CONCLUSIONS

The modified PB theory, which includes restrictions on maximum attainable concentration of ions in a solution Cmax determined by their finite sizes, has been employed to study (under the conditions of constant surface charge density σs) the spatial distributions of the electrostatic potential in a 1 : 1 electrolyte near a spherical particle. It has been found that, for weakly charged particles, the potential profiles are almost independent of Cmax and coincide with the profile obtained in terms of the classical PB model. The surface potential gradually increases with σs. Far from a charged particle, when the potential decreases below its thermal value, an exponential drop of the potential is observed for all considered ion sizes. In contrast to the classical PB theory, according to which a rise in the surface charge leads to potential saturation \(\left| {{{\psi }_{{{\text{eff}}}}}} \right| \to 4,\) in the modified PB theory, which takes into account the sizes of electrolyte ions in the simplest form, the effect of saturation is absent. Now, the value of \({{\psi }_{{{\text{eff}}}}}\) depends (in accordance with the results of the performed calculations) on both the surface charge and the size of counterions. Moreover, for large counterions, the effective potential substantially exceeds the corresponding value obtained by solving the nonlinear MPBE. The difference in the EDL characteristics obtained by solving the classical and modified PB equations directly follows from the fact that the modified theory predicts the appearance of a condensed layer at a particle surface, with the concentration of counterions in this layer being equal to Cmax. Therewith, the layer thickness increases with a rise in the surface charge density (at a constant ion size) and ion size (at a constant charge density on the particle surface ).