INTRODUCTION

Rayleigh surface acoustic waves (RSAWs) are traditionally used in flaw detection to detect surface defects. Recently, however, RSAWs have also found application in problems of acoustic structurometry [1], in assessing stresses and residual deformations [2–4], the level of fatigue damage [5, 6], RF Patent no. 2507514], and in many other technical problems.

For many highly loaded structures, the accumulation of operational damage follows the mechanism of the growth of microplastic deformations and depletion of plasticity. In this regard, the increased interest of modern researchers in studying the effect of plastic deformation on the acoustic characteristics of material, including such unconventional ones as the parameters of structure-borne noise (hereinafter referred to as SN) is understandable. Structural noise is associated with the scattering of elastic waves on structural inhomogeneities, nonmetallic inclusions, and metal grains. In this case, SN is present both in the domain of the probing pulse and after the passage of this pulse.

There are various radio engineering methods for processing signals containing “noise” characteristics. Among those, one can distinguish such methods as spatial–temporal processing, optimization of scanning parameters [7, 8], wavelet filtering [10], radio technical methods of SN “whitening” [11], etc.

It should be noted that in modern studies, SN is considered not only as a hindrance but also as a source of information about the structure of material by which one can judge its state [11–13]. The problem lies in the development of reliable algorithms for obtaining this information.

The reliability of the above-mentioned algorithms is determined, firstly, by the correctness of the used mathematical methods for processing the results of acoustic measurements in order to determine the informative SN characteristics and, secondly, by the adequacy of these characteristics to the monitored parameters of the materials under study.

In [14], an approach was formulated to assessing the structure of metal based on the value of the integral level of acoustic SN, for which the SN averaged amplitude was used, and the effect of the grain size of steel 45 on the value of the proposed SN characteristic was also shown experimentally. The relationship between SN and porosity was shown in [15]. In the papers [16, 17], a method of ultrasonic structuroscopy of products made of complex-structured materials was proposed that uses the analysis of SN statistical characteristics. The authors have shown that a comprehensive analysis of SN signal makes it possible to establish a relationship between its energy spectrum and the nature of the structural inhomogeneities in the material under study.

Analyzing changes in the SN energy spectrum in the same material allows monitoring changes in its structure during operation—if a change in the energy spectrum is recorded when observing the same object over time, then this indicates the emergence of deformations in the material [16].

At the same time, it was noted that special materials science studies are required to establish stable quantitative relationships between SN characteristics and the parameters of the structure of specific products.

The papers [18–22] as well as RF Patent no. 2589751 are devoted to structural inspections using the characteristics of a backscattered signal.

It should be noted that the currently used methods of wavelet processing of various signals, including ultrasonic pulses, are often characterized by redundancy of information, which can be useful, for example, for neural network models in the absence of intelligible physical ideas about the phenomena under study. In the case of analyzing the regularities of elastoplastic deformation by the acoustic method, when the nature of SN is understood at the level of rigorous physical concepts, it is hardly advisable to use wavelet analysis algorithms. Indeed, in its nature the energy spectrum of acoustic SN does not differ much from the spectrum of the probing pulse. In this regard, using wavelet analysis to obtain the quantitative characteristics of SN can increase the errors in estimating the spectral–energy characteristics, since the assumption of the quasi-steadiness of SN and its processing by means of the short-time fast Fourier transform (FFT) leads to substantially smaller errors than the results of wavelet analysis of real oscillograms as nonstationary processes.

A comparative analysis of the experimental results obtained by various researchers showed that when analyzing the parameters of microstructure, micropores, microcracks, and other microdamages that provide the Rayleigh character of pulse scattering in the megahertz range, the parameters of the energy spectrum of SN should be considered as the most informative characteristics.

The aim of this work is to develop an algorithm for the quantitative assessment of structure-borne noise when using RSAW pulses, based on the calculation of their relative energy, as well as experimental verification of the proposed algorithm under elastic and elastoplastic deformation of 20GL steel widely present in railway transport.

ALGORITHM FOR ASSESSING STRUCTURE-BORNE NOISES

To obtain the necessary quantitative spectral-energy estimates, we used the short-time Fourier transform of the signal \(U\left( t \right),\)

$$S\left( {\omega ,\tau } \right) = \int\limits_{ - \infty }^\infty {U(t)} W(t - \tau ){{e}^{{ - \omega t}}}dt,$$
(1)

where \(S\left( {\omega ,\tau } \right)\) is the spectral density, depending on the frequency ω and the time shift \(\tau \), \(W\left( t \right)\) is a tapering function, the choice of which is determined by the specific features of the problem being solved and the required accuracy of time and frequency resolution. A discrete analogue of expression (1) has the form

$$S({{\omega }_{k}}) = \sum\limits_{n = 0}^{N - 1} {} u(n\Delta t)w(n\Delta t){{e}^{{ - j{{\omega }_{k}}n\Delta t}}},$$
(2)

where \({{\omega }_{k}}\) are discrete frequencies, \(u\left( {n\Delta t} \right)\) are signal samples, \(N\) is the number of equidistant samples within the signal observation interval \(T\), \(w\left( {n\Delta t} \right)\) are the samples of the tapering function; \({{w}_{k}} = \frac{{2\pi }}{{N\Delta t}}k\), \(k = 0,1, \ldots ,N - 1\), and \(t = \frac{T}{N}\) is the signal sampling step, inverse to the sampling frequency \({{f}_{{\text{d}}}}\).

In digital processing, it is usually assumed that \(\Delta t = 1\); therefore, formula (2) is written as

$${{S}_{k}} = \sum\limits_{n = 0}^{N - 1} {{{u}_{n}}{{w}_{n}}{{e}^{{ - j\frac{{2\pi }}{N}kn}}}.} $$
(3)

When processing SN realizations, the main criterion for the tapering function is the requirement for the maximum suppression of spectrum spreading (the Gibbs effect). To fulfill this criterion, the following parameters need to be optimized: the main lobe width at –3 dB, the main lobe width at the zero level, the maximum side lobe level, and the window attenuation coefficient.

One of the best functions according to the listed criteria is the Hamming tapering function [23]

$${{w}_{n}} = \left\{ \begin{gathered} 0.53836 - 0.46164\cos \frac{{2\pi }}{N}n,\,\,\,\,n = 0,1,...N - 1 \hfill \\ 0,\,\,\,\,n \geqslant N \hfill \\ \end{gathered} \right.,$$
(4)

which we will use.

One of the most promising methods for calculating the SN energy spectrum is its determination using a modified periodogram by the Welch method [24], which provides, as shown in [25], a consistent estimate of the power density value \({{P}_{k}} = {{\left| {{{S}_{k}}} \right|}^{2}}\).

When dividing the array of structure-borne noise values with a total duration of \({{N}_{n}}\) into \({{N}_{{{\text{seg}}}}}\) segments, the expression for the modified periodogram takes the form

$${{\Pi }_{k}}(i) = \frac{1}{U}\left| {\sum\limits_{n = 0}^{{{N}_{{\text{p}}}} - 1} {{{u}_{n}}(i){{w}_{n}}(i){{e}^{{ - j\frac{{2\pi }}{{{{N}_{{\text{p}}}}}}kn}}}} } \right|,$$
(5)

where \({{N}_{{\text{p}}}}\) is the periodogram duration, \(i = 1,...,{{N}_{{{\text{seg}}}}},\) and \(\frac{1}{U}\) is the Welch weight factor

$$U = \frac{{\sum\limits_{n = 0}^{{{N}_{{\text{p}}}} - 1} {{{{\left| {{{w}_{n}}(i)} \right|}}^{2}}} }}{{{{N}_{{\text{p}}}}}}.$$
(6)

The total number of segments \({{N}_{{{\text{seg}}}}}\) depends on the noise duration \({{N}_{{\text{n}}}}\), the periodogram duration \({{N}_{{\text{p}}}}\), and the degree of overlap of the segments \({{t}_{s}},\% ,\)

$${{N}_{{{\text{seg}}}}} = {\text{Int}}\left[ {\frac{{{{N}_{{\text{n}}}} - {{N}_{{\text{p}}}}}}{{{{N}_{{\text{p}}}}\left( {1 - \frac{{{{t}_{s}}}}{{100}}} \right)}} + 1} \right],$$
(7)

where the operator \({\text{Int}}\) designates the entier of the bracketed expression.

The expression for the spectral power density in accordance with [30] has the form

$${{P}_{k}} = \frac{1}{{{{N}_{{{\text{seg}}}}}}}\sum\limits_{i = 1}^{{{N}_{{{\text{seg}}}}}} {{{\Pi }_{k}}(i).} $$
(8)

As an informative quantitative characteristic of structure-borne noise, we will use the value of the relative energy

$$\delta {{E}_{{\text{n}}}} = \frac{{{{E}_{{\text{n}}}}}}{{{{E}_{\Sigma }}}},$$
(9)

where \({{E}_{{\text{n}}}}\) is the noise energy calculated by the formula

$${{E}_{{\text{n}}}} = \frac{1}{{{{N}_{{\text{p}}}}}}\sum\limits_{k = 0}^{{{N}_{{\text{p}}}} - 1} {{{P}_{k}}} ,$$
(10)

\({{P}_{k}}\) is calculated by formula (8).

The \({{E}_{\Sigma }}\) is the total energy of noise and signal,

$${{E}_{\Sigma }} = {{E}_{{\text{n}}}} + {{E}_{{\text{s}}}},$$
(11)

and \({{E}_{{\text{s}}}}\) is the signal energy calculated by the formula

$${{E}_{{\text{c}}}} = \sum\limits_{k = 0}^{{{N}_{{\text{s}}}} - 1} {{{{\left| {\sum\limits_{n = 0}^{{{N}_{{\text{0}}}} - 1} {{{u}_{n}}{{w}_{n}}{{e}^{{ - f\frac{{2\pi }}{N}kn}}}} } \right|}}^{2}}} $$
(12)

for the Hamming tapering function (4).

MATERIALS AND METHODS

A quantitative assessment of the value of the relative energy of structure-borne noise was carried out using samples of steel 20GL with a yield point of 210 MPa. We used flat reference blocks of type I according to GOST (State Standard) 1497 with a thickness of the working part of 5 mm. The roughness of the working surface \({\text{Ra}}\) was 2.5 \(\mu {\text{m}}\) in accordance with GOST (State Standard) 2589. The measurements were repeated for 5 identical samples. Each measurement was repeated 5 times with the breakdown of the acoustic contact.

Elastoplastic deformation of the samples was carried out using a Tinius OIlsen Ltd testing machine, model H100KU.

Acoustic measurements were taken using the ASTRON IVK (no. 67552-17 in the State Register of Measuring Instruments); this makes it possible to accurately measure the delays and amplitudes of ultrasonic pulses.

The measurements were carried out at the moments when the upper traverse of the testing machine stopped. The tensile curve with traverse stopping points indicated is shown in Fig. 1.

Fig. 1.
figure 1

Tensile curve, steel 20GL.

Full size image

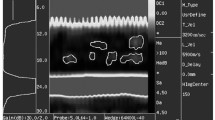
RSAW pulses with a frequency of 3 MHz and a duration of approximately 2 \(\mu {\text{s}}\) were excited and received using a wedge-shaped sensor with a fixed measurement base (Fig. 2). Plexiglas® was used as the material of the wedge-shaped sensor. The angle \(\alpha \) was chosen equal to the second critical angle. A typical oscillogram of a RSAW pulse is shown in Fig. 3.

Fig. 2.
figure 2

Design of the wedge-shaped surface wave sensor: (1) double-sided Plexiglass® wedge, (2) emitter of Rayleigh waves, (3) receiver of Rayleigh waves, (4) casing, (5) high-frequency cable.

Full size image
Fig. 3.
figure 3

Oscillogram of surface wave signal.

Full size image

In Fig. 3, the analyzed SN area corresponds to the pulse scattered in the direction of wave propagation.

Backscattering is not taken into account in the framework of the developed algorithm, since its main parameters (average amplitude, energy, etc.), as shown by experiments, are characterized by a substantial scatter, almost an order of magnitude higher than the corresponding values for forward scattering.

The duration of SN was determined by the degree of its attenuation to the noise level of equipment and calculated by means of the ASTRON IVK software.

Spectral processing was carried out using FFT with a number of points of 213, which corresponds to a frequency resolution of 20 kHz for the sampling rate of 160 MHz.

Figure 4 shows typical energy spectra.

Fig. 4.
figure 4

Typical energy spectra of pulse (a) and structure-borne noise (b) obtained for samples in the initial state.

Full size image

Measurements were repeated 5 times at each stage of loading.

The results of measurements of the relative values of structure-borne noise are compiled in Tables 1 (elastic deformation) and 2 (elastoplastic deformation).

Table 1. Elastic deformation
Full size table

In the tables, \(\left\langle {\delta {{E}_{{\text{n}}}}} \right\rangle \) is the average value of the relative energy of structure-borne noise and \(\Delta \left( {\delta {{E}_{{\text{n}}}}} \right)\) is the confidence interval at a confidence level of 95%. The test results showed that in the domain of elastic deformations (see Table 1) the average value of the relative energy of structure-borne noise remains constant, while in the region of elastoplastic deformations (see Table 2) the relative energy of structure-borne noise depends on the plastic deformation of the samples. The corresponding graph of dependence for elastoplastic deformations is shown in Fig. 5.

Table 2.   Elastoplastic deformation
Full size table
Fig. 5.
figure 5

Influence of plastic deformation on the relative energy of structure-borne noise.

Full size image

When constructing the graphs, the true values of deformations \({{\varepsilon }_{{{\text{true}}}}}\) and stresses \({{\sigma }_{{{\text{true}}}}}\) were used, which at the stage of uniform deformation are expressed via the conditional values \({{\varepsilon }_{{{\text{cond}}}}}\) and \({{\sigma }_{{{\text{cond}}}}}\) as follows:

$${{\varepsilon }_{{{\text{true}}}}} = \ln \left( {1 + {{\varepsilon }_{{{\text{cond}}}}}} \right),$$
(13)
$${{\sigma }_{{{\text{true}}}}} = {{\sigma }_{{{\text{cond}}}}}\left( {1 + {{\varepsilon }_{{{\text{cond}}}}}} \right).$$
(14)

Figure 6 shows the curve of the dependence of the relative noise energy on the true stress for the entire region of elastoplastic deformation.

Fig. 6.
figure 6

Dependence of relative noise energy on true stress for the entire deformation diagram.

Full size image

The curve in Fig. 6 allows an interesting conclusion about the nature of the effect of stress on the used parameter \(\delta {{E}_{{\text{n}}}}\). Regardless of whether the material is in the region of elastic or elastoplastic deformation, the dependence curve is described by the single-valued function

$$\delta {{E}_{{\text{n}}}} = \left\{ \begin{gathered} \delta {{E}_{{\text{n}}}}({\text{elast)}} = {\text{const}}\,\,{\text{for}}\,\,{\text{0}} \leqslant {{\sigma }_{{{\text{true}}}}} < {{\sigma }_{{\text{y}}}} \hfill \\ {{f}_{1}}({{\sigma }_{{{\text{true}}}}})\,\,{\text{or}}\,\,{{f}_{2}}\left( {{{\varepsilon }_{{{\text{true}}}}}} \right)\,\,{\text{for}}\,\,{{\sigma }_{{{\text{true}}}}} < {{\sigma }_{{\text{y}}}} \hfill \\ \end{gathered} \right..$$
(15)

where \({{\sigma }_{{\text{y}}}}\) is the physical yield stress and the approximating functions \({{f}_{1}}\left( {{{\sigma }_{{{\text{true}}}}}} \right)\) and \({{f}_{1}}\left( {{{\varepsilon }_{{{\text{true}}}}}} \right)\) are easy to select by the least squares method.

In the practical usage of the proposed algorithm for a real structural element or a semifinished product made of steel 20GL, the approximating dependences (15), taking into account the errors in determining the proposed informative structure-borne noise parameter listed in Tables 1 and 2, will make it possible to determine the parameters of the stress-strain state of material in the elastoplastic region; this is extremely important when solving both technological problems and the problems of safe operation of various objects.

CONCLUSIONS

(1) Modern approaches to the processing of ultrasonic signals containing an uncorrelated component in the form of structure-borne noise have been analyzed.

(2) A variant of quantitative assessment of structure-borne noise when using RSAW pulses is proposed. It is based on the calculation of the relative energy of structure-borne noise using a short-time Fourier transform and a modified Welch periodogram method.

(3) It has been shown experimentally that elastic stresses do not affect the value of structure-borne noise when using RSAWs, in agreement with the conclusions of [26, 27].

(4) Plastic deformation has a considerable effect on the value of structure-borne noise starting with the yield point; this can be associated with the well-known processes of an increase in the spatial inhomogeneity of plastically deformed polycrystals at the mesoscale.

(5) The results obtained can serve as a basis for the development of an engineering technique for assessing stresses or the degree of plastic deformation of a structural material, regardless of what state—elastic or elastoplastic—it is in; this is not allowed by velosymmetric methods due to the simultaneous (multidirectional and depending on the type of the stress state) effect on the speed of sound of elastic and plastic deformations.