Comparative Analysis of Neural Networking and Regression Models for Time Series Forecasting

Abstract

Applicability of neural nets in time series forecasting has been considered and researched. For this, training of fully connected and recurrent neural networks on various time series with preliminary selection of optimal hyperparameters (optimization algorithm, amount of neurons on hidden layers, amount of epochs during training) has been performed. Comparative analysis of received neural networking forecasting models with each other and regression models has been performed. Conditions, affecting on accuracy and stability of results of the neural networks, have been revealed.

INTRODUCTION

Nowadays there are various classes of forecasting models and methods. Forecasting models can be divided into two categories. In statistical models, dependence of value of time series on previous values of the same time series is expressed by a formula. In structural models, this dependence is set by some structure [1]. These models are used, when finding the dependence analytically seems to be difficult.

Neural networks are attributed to structural category of forecasting models. In these models, unlike in statistical ones, not only initial data affect accuracy and stability of forecasting results, but several structural characteristics of neural networks (such as amount of neurons and connections among them, activation functions, training duration, etc.) also do. This is a disadvantage of neural networks, which complicates their using in forecasting. That’s why comparing of statistical and structural approaches to time series forecasting is of interest.

FEATURES OF NEURAL NETWORK MODELS FOR TIME SERIES ANALYSIS AND FORECASTING

The aim of this research is building and researching two neural networks, analyzing various time series. The following objectives have been set:

– setting of optimal values of neuronet hyperparameters;

– comparing of accuracy results of neural networks and regression models for time series with linear and non-linear trends.

Two neural networks are the object of the researching: perceptron and recurrent neural network. Perceptron consists of three sequential layers. The choice of this architecture is due to the fact that, on the one hand, neural networks with one hidden layer are universal approximators [2], and on the other hand, using of deep neural networks doesn’t improve results in comparison with neuronets with 1–2 hidden layers [3]. Input layer consists of p neurons, to which p consecutive elements of the considered time series are fed. After the input layer, the network has a hidden one, consisting of arbitrary amount of neurons. On this layer, activation function ReLU (rectified linear unit) is acting according to the following formula:

$$f(x) = \max (0,x).$$

(1)

Output layer consists of the only neuron, on which prediction of value of time series from p previous values (lags) is calculated. This neural network is fully connected, i.e. all neurons of each layer (except the output one) are connected with all neurons of the next layer by directed connections (synapses) with own weights. Besides, input data are preliminarily normalized according to the following formula:

$$x{\kern 1pt} ' = \frac{{x - {{x}_{{\min }}}}}{{{{x}_{{\max }}} - {{x}_{{\min }}}}},$$

(2)

where x – value before normalizing, x' ∈ [0, 1] – value after normalizing, x_min and x_max – minimal and maximal values of the considered time series respectively. The inverse of (2) is applied to the result obtained on the output layer. As a result, forecasted value of the time series is received.

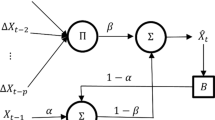
As the perceptron, the recurrent neural network consists of three layers. Input layer contains p neurons, output one – single neuron, and all neurons on input and hidden layers are connected with all neurons on hidden and output layers respectively. Unlike the perceptron, the recurrent neuronet hidden layer contains LSTM neurons, presenting a kind of recurrent neurons, which can use the value on their outputs on the next epoch, as well as remember input information [4]. On hidden layer, two activation functions are used: one function for data from input layer, and the other one for data, obtained on hidden layer and fed recurrently on input of LSTM neurons. In considered neural network, activation functions ReLU (1) and hard sigmoid, acting according to the following formula:

$$f(x) = \left\{ \begin{gathered} 0,\quad x < - 2.5, \hfill \\ 0.2x + 0.5,\quad - {\kern 1pt} 2.5 < x < 2.5, \hfill \\ 1,\quad x > 2.5, \hfill \\ \end{gathered} \right.$$

are used respectively.

As in the perceptron, input data are normalized according to formula (2), and then are fed to input of the recurrent neural network, producing a forecasting result, to which inverse transformation must be applied.

HYPERPARAMETERS EVALUATION SCHEME AND ANALYSIS OF THE NEURAL NETWORKS PERFORMANCE

Algorithm that implements the neural networks has been implemented on R language with using Keras library [5, 6]. Building of neural networking models for each series is performed with training of the neural networks.

Training of the neural networks occurs as follows. Initially, n–p training instances, where n – length of the considered time series, are formed. Each of them is a vector of p consecutive elements of time series, to which the next, (p + 1)th element of the same series, is mapped. After that, the neural networks are trained on these instances for several epochs. Thus, the neural networks have the following hyperparameters, which should be evaluated:

– amount of neurons on the input layer p (which is also indicates maximal lag order, with which forecasting of the series will be performed);

– amount of neurons on the hidden layer;

– amount of training epochs.

Neural networks optimization algorithm, i.e. algorithm of synapses weights recalculation on each epoch, has been selected by example of modeled time series with deterministic quadratic trend:

$${{y}_{t}} = a + bt + c{{t}^{2}} + {{\xi }_{t}},\quad t = \overline {1,n} ,$$

(3)

where y_t – value of the time series in moment t, a, b and c – trend parameters, ξ_t, $t = \overline {1,n}$ – random values, which are normally distributed with zero mean and preset variance σ².

After the selection of optimization algorithm, hyperparameters evaluation was done on an example of the series (3). Training of the neural networks with various sets of values of hyperparameters was performed. For each of these sets training was repeated Q times. After each training, mean absolute error (MAE) was calculated according to the following formula:

$${{e}_{q}} = \frac{1}{{n - p}}\sum\limits_{t = p + 1}^n {\left| {{{y}_{t}} - {{{\hat {y}}}_{{q,t}}}} \right|} ,\quad q = \overline {1,Q} ,$$

(4)

where ${{\hat {y}}_{{q,t}}}$, $t = \overline {p + 1,n}$, $q = \overline {1,Q}$, – forecasted values of the time series y_t. For received values e_q, $q = \overline {1,Q}$, their mean value and standard deviation were calculated. After comparison of these characteristics, the set of optimal values of hyperparameters has been selected.

In Table 1, results of the perceptron and LSTM network performance, when using different optimization algorithms for the time series (3), are presented (the experiment has been repeated Q times for each optimizator).

Table 1. Comparison of the neural networks performance on an example of series y_t = a + bt + ct² + ξ_t, $t = \overline {1,n}$, ξ_t ∈ N(0, σ²). Results for a = 21.4, b = 3.2, c = 0.07, n = 1109, σ = 15, Q = 25 are presented

As Table 1 shows, for the majority of optimization algorithms implemented in Keras library, standard deviation of MAEs exceeds their mean value, which indicates instability of both neural networks in these cases. That’s why adaptive gradient method, or AdaGrad, has been chosen as optimization algorithm for training both neuronets, because it has demonstrated the best stability in comparison to other optimizators.

Given method is a modification of the method of stochastic gradient descent (SGD), which is widely used for training of neural networks. Unlike SGD, where the length of a gradient vector, along which weights of synapses change, doesn’t depend on input data, in AdaGrad, frequency of input instances is taken into account to take notice of infrequently occurring values of time series, which can impact on the desired models [7]. If in stochastic gradient descent, parameters of optimizator θ_i, $i = \overline {1,\nu }$, are recalculated according to formula

$${{\theta }_{{\tau + 1,i}}} = {{\theta }_{{\tau ,i}}} - \eta \cdot {{\nabla }_{\theta }}J({{\theta }_{{\tau ,i}}}),$$

where θ_τ,i – value of parameter in the beginning of τth epoch, η – hyperparameter, called “general learning rate”, than when using adaptive gradient, the following transform is taking place:

$${{\theta }_{{\tau + 1,i}}} = {{\theta }_{{\tau ,i}}} - \frac{\eta }{{\sqrt {{{G}_{{\tau ,ii}}} + \varepsilon } }} \cdot {{\nabla }_{\theta }}J({{\theta }_{{\tau ,i}}}),$$

where G_τ – diagonal matrix of the order of ν, in which ith diagonal element equals to the sum of the squares of the partial derivatives of the function J with respect to parameter θ_i, which are received on the first τ epochs, ε – smoothing variable that avoids division by zero (usually on the order of $1 \times {{10}^{{ - 8}}}$) [8].

After hyperparameters evaluation, the neural networks have been applied for building of forecasts for the following series with deterministic trends:

$$\begin{gathered} {{y}_{t}} = a + bt + {{\xi }_{t}}, \\ {{y}_{t}} = a + bt + c\sin t + {{\xi }_{t}}, \\ {{y}_{t}} = a + bt + c{{t}^{2}} + {{\xi }_{t}}, \\ {{y}_{t}} = a\sin t + b{{t}^{2}} + {{\xi }_{t}}, \\ {{y}_{t}} = a + b\sin t + {{\xi }_{t}}, \\ \end{gathered} $$

where a, b, c – trend parameters, ξ_t ∈ N(0, σ²). Synapses weights initialization for the given series was done randomly. After training of the neural network, MAE was calculated according to formula (4). This procedure was repeated Q times for each time series.

For each time series a linear regression model

$${{y}_{t}} = \alpha + \beta t + {{\xi }_{t}},\quad t = \overline {1,n} $$

(5)

was built by ordinary least squares, as well as autoregression model:

$${{y}_{t}} = {{\beta }_{1}}{{y}_{{t - 1}}} + ... + {{\beta }_{p}}{{y}_{{t - p}}} + {{\xi }_{t}},\quad t = \overline {p + 1,n} .$$

(6)

For both models MAEs were calculated with formula (4) (for model (5) p = 0 was considered). These MAEs were compared with statistical characteristics of MAEs received for the perceptron and LSTM network.

RESEARCH RESULTS

Examples of the neural networks performance with various values of hyperparameters are presented in Table 2.

Table 2. Accuracy of the neural networks performance on an example of the series y_t = a + bt + ct² + ξ_t, $t = \overline {1,n}$

The perceptron with ten neurons on its hidden layer is less accurate and stable, because mean and standard deviation of MAEs in this occurrence exceed values of the same characteristics with other amount of neurons on the hidden layer. In other occurrences, connection between amount of neurons on the input and on the hidden layers is not clearly visible. And for the recurrent neural network, optimal amount of neurons on hidden layer is about 100–500. If there are fewer neurons, less stable results are obtained, and if there are more neurons, training of LSTM network takes longer without significant improvement of results. Among all considered results, the best ones received, when amount of neurons on the hidden layer is 100, p ∈ {3, 5, 7} (values of p ∈ {3, 5, 7, 10, 15}, amount of neurons on the hidden layer from set {10, 50, 100, 250, 500, 1000} for the perceptron and {10, 50, 100, 250, 500} for the LSTM network have been considered).

Dependence of accuracy of the perceptron performance on amount of neurons on the hidden layers for time series of various lengths has been also considered. Examples of results are presented in Table 3.

Table 3. Accuracy of the perceptron performance on an example of the series y_t = a + bt + ct² + ξ_t, $t = \overline {1,n}$

The best accuracy and stability results have been received for the following pairs of value of n and amount of neurons: (1000, 5000), (1000, 10 000), (2500, 5000), (2500, 10 000), (5000, 5000), (5000, 10 000), (10 000, 2500), (10 000, 5000) (series of length of n ∈ {1000, 2500, 5000, 10 000} and amount of neurons from set {100, 500, 1000, 5000, 10 000, 20 000, 40 000} were considered). When n = 1000, approximately equal results have been received for various amounts of neurons on the hidden layer. For others values of n, the neural network has demonstrated the best accuracy and stability with 2500–10 000 neurons.

On a computer with a processor Intel® Core™ i5-3230M CPU 2.60 GHz, average time of the perceptron training for series with length n = 1000 – 9 seconds per epoch, with n = 10 000 – 82 seconds, and it doesn’t depend on amount of neurons. Training was performed for 5–10 epochs, because with further training accuracy of the perceptron results is insignificantly changed (Figs. 1, 2).

Fig. 1.

Dynamics of mean absolute errors for normalized data after each epoch during the perceptron training for forecasting of series y_t = a + bt + ct² + ξ_t.

Fig. 2.

Dynamics of mean absolute errors for normalized data, when forecasting series y_t = a + bt + c sin t + ξ_t with perceptron.

Figures 1, 2 show that significant improvement of the results for various time series is reached after the second epoch. For example, for time series with quadratic trend (Fig. 1) MAE of normalized data has decreased with comparison to the first epoch. With further training MAE either remains almost unchanged (Fig. 1) or slowly decreases (for example, for series y_t = a + bt + c sin t + ξ_t (Fig. 2) MAE after the 12th epoch was 2.3 × 10^–3, and after the 24th epoch – 2.2 × 10^–3, i.e. after increasing the amount of epochs by 2 times the results increased by 23/22 ≈ 1.045 times).

Analysis of the recurrent neural network in forecasting time series with length n = 1000 has also been performed. Average training time of LSTM network is 9 s, when there are 100 neurons on hidden layer, 14 s, when there are 250 neurons, and 50 s, when there are 500 neurons (Figs. 3–6).

Fig. 3.

Dynamics of mean absolute errors for normalized data, when forecasting series y_t = a + bt + ct² + ξ_t with LSTM-net with 100 neurons on hidden layer.

Fig. 4.

Dynamics of mean absolute errors for normalized data, when forecasting series y_t = a + bt + ct² + ξ_t with LSTM-net with 500 neurons on hidden layer.

Fig. 5.

Dynamics of mean absolute errors for normalized data, when forecasting series y_t = a + bt + c sin t + ξ_t with LSTM-net with 100 neurons on hidden layer.

Fig. 6.

Dynamics of mean absolute errors for normalized data, when forecasting series y_t = a + bt + c sin t + ξ_t with LSTM-net with 500 neurons on hidden layer.

With 100 neurons on hidden layer of the LSTM network training is as long as training of the perceptron, but such net is less accurate compared to the fully-connected neuronet. On the other hand, with using 500 neurons on hidden layer, one can obtain more accurate results, but such LSTM network will be trained significantly longer. Thus, recommended amount of epochs for the recurrent neural network will depend not only on length of considered time series, but also on architecture of the neural network itself.

Further, dependence of accuracy of the neural networks performance on parameters a, b, c, σ with p = 7 and 100 neurons on the hidden layer was considered. There were 7 epochs during training of the perceptron, and 10 epochs during training of the LSTM network. Received characteristics of MAEs and their comparison to MAEs of regression models for series with linear trend are presented in Table 4 (in Tables 4–8, “S.d.” stands for “standard deviation”, “LR MAE” and “AR MAE” denote MAEs obtained with linear regression and autoregression respectively).

Table 4. Comparison of accuracy of neural networking models with regression models for series y_t = a + bt + ξ_t, $t = \overline {1,n}$, ξ_t ∈ N(0, σ²)

Table 5. Comparison of neural networking models with regression models for series y_t = 1 + t + csint + ξ_t, $t = \overline {1,n}$, ξ_t ∈ N(0, σ²)

Table 6. Comparison of neural networking models with regression models for series y_t = 1 + t + ct² + ξ_t, $t = \overline {1,n}$, ξ_t ∈ N(0, σ²)

Table 7. Comparison of neural networking models with regression models for series y_t = a sin t + bt² + ξ_t, $t = \overline {1,n}$, ξ_t ∈ N(0, σ²)

Table 8. Comparison of neural networking models with regression models for series y_t = a + b sin t + ξ_t, $t = \overline {1,n}$, ξ_t ∈ N(0, σ²)

For all series with linear trends, both neural networks are more accurate than autoregression model (6), but less accurate than linear regression (5). Besides, mean absolute error of the model (5) doesn’t depend on free term and coefficient, which set linear trend of series, while when modeling with both the perceptron and the LSTM network, with the increasing of b the accuracy and stability of the results get worse. Variance σ² also impacts on the accuracy and stability of the results.

In Tables 5–8, accuracy results and comparison of the models for series with non-linear trends are presented.

When forecasting time series with linear trend and sinusoidal oscillations, variance σ² of random values ξ_t plays an important role: its increasing involves increasing of MAEs with all the models. The recurrent neural network gives more stable results than the perceptron, as evidenced by the values of standard deviations of MAEs.

When forecasting series with quadratic trend, trend parameter c also impacts on performance of the models. By increasing of this parameter accuracy and stability of the neural networking models get worse, as well as accuracy of regression models. The LSTM network has shown better results in stability in comparison with the perceptron.

For series y_t = a sin t + bt² + ξ_t with increasing of coefficient b MAEs with neural networks and autoregression increase, and with autoregression changing of the results is more substantial. The recurrent neural network has shown better results than the perceptron in all the examples, except a = 10, b = 0.1. Influence of parameters a and σ is less significant.

For series with no trend and with sinusoidal oscillations, forecasting accuracy exclusively depends on variance σ².

On the whole, from Tables 5–8 we can conclude that for series with non-linear trends neural networking models better fit. Series y_t = 1 + t + c sin t + ξ_t with c = 1 and c = 10 are exceptions (Table 5). In this occurrence, non-linear component csint, which varies from –c to c, has less impact on behavior of the series, than random values ξ_t, which are in interval (‒3σ, 3σ), i.e. from –3 to 3, from –30 to 30 and from –150 to 150 for the suggested examples. That’s why the results of the perceptron and the LSTM network are similar to the results with series with linear trend, and neural network works worse than linear regression model (5).

Besides, for series y_t = a sin t + bt² + ξ_t with a = 50, b = 0.02 and y_t = a + b sin t + ξ_t (Tables 7 and 8) the results of the perceptron are bit worse than ones of autoregression model (6). This is due to the fact that for these series a strongly marked periodicity is inherent, by virtue of which an apparent dependence of value of time series on its past values is taking place, and this dependence can be evaluated with autoregression model. At the same time, results of the LSTM network for series y_t = a sin t + bt² + ξ_t are better than ones of the perceptron and autoregression.

With increasing of variance of random values ξ_t the accuracy of neural networks decreases, and an influence of variance on the stability is not visible. Parameters, setting trend of time series, principally impact on the accuracy of the models, but the stability not always depends on them. For example, in series y_t = 1 + t + ct² + ξ_t with increasing of parameter c standard deviation of MAEs also significantly increases (Table 6), but in other cases there is no such an obvious dependence.

CONCLUSIONS

From the research results we can conclude than perceptrons and LSTM networks with single hidden layer can be used in time series forecasting. Selection of values of hyperparameters is important, because it impacts on accuracy and stability of the neural networks. The impact of selection of optimization algorithm during neural networks training was also shown.

Comparative analysis of neural networking models with each other, as well as with linear regression and autoregression, has been performed. Its result is that linear regression better approximates series with linear trends, autoregression and the LSTM network – series with periodicity and the perceptron better works with non-periodical series with non-linear trends. The perceptron training time only depends on length of forecasted time series, and training time for the recurrent neural network depends also on amount of neurons on hidden layer of the network. At the same time, with proper choosing of this amount the LSTM network gives more accurate and stable results than the perceptron, as a rule. Thus, with the considered neural networks it’s possible to build a forecast for arbitrary time series with deterministic trend for a limited time.