An Integrally Asymmetric Flow Past a Plate with an Upstream-Moving Surface

Abstract

This paper considers the flow of a viscous ideal gas past a plate with an upstream-moving surface. A new type of nonstationary periodic flow with integral asymmetry of aerodynamic characteristics is discovered at transonic free-stream velocities.

INTRODUCTION

The problem of flow past a fixed plate with a surface moving against an incompressible fluid flow was studied in [1–4], where it was found that, within the framework of the boundary layer equations, a solution exists only for a relative velocity of the plate surface β less than 0.3541. For greater β the solution was already obtained in the framework of the Navier–Stokes equations [5]. At a plate surface velocity greater than the free-stream velocity, the flow near the plate becomes unsteady and periodic in time [6]. In the range $1 \leqslant \beta \leqslant 1.6$, the period depends weakly on β and is about 25 times greater than the duration of the free stream passing the plate length. A lifting force arises and acts on the plate. The lifting force is positive for half of the period and negative for the other half. After integrating over the period, the average lifting force amounts to zero.

This work focuses on the flow near a plate with an upstream-moving surface in compressible gas at transonic speeds, which is typical for modern aircraft. Moving surfaces can be used to control the flow. There are barely any theoretical studies of such flows at transonic speeds. As a result of analysis of the solution, a new phenomenon was discovered—an unsteady, asymmetric, on average, change in the flow characteristics near the plate at some modes of velocity of the flow and the plate surface.

PROBLEM SETUP

Consider a two-dimensional flow past a fixed plate at a zero angle of attack to free-stream velocity u_∞ of a viscous perfect gas. The velocity of both plate surfaces is directed against the incident flow and is equal in magnitude to $\beta {{u}_{\infty }}$.

The plate length is L. The free-stream Mach number is M_∞. The characteristic Reynolds number Re is based on the free-stream velocity, plate length, and the kinematic viscosity coefficient of the unperturbed flow. t is time nondimensionalized by ${L \mathord{\left/ {\vphantom {L {{{u}_{\infty }}}}} \right. \kern-0em} {{{u}_{\infty }}}}$, and the Prandtl number $\Pr$ and adiabatic exponent k are assumed constant.

The parameters of a uniform flow are set at an infinite distance from the plate, and the no-slip condition and the temperature factor η, which is equal to the ratio of the plate temperature to the stagnation temperature of the incident gas, are set on the surface. The flow is assumed to be laminar with a viscosity coefficient determined by the Sutherland law.

The calculations were carried out using the finite volume method on structured grids. The rectangular boundary of the computational domain was located at a distance of 25 plate lengths from the plate. The program was tested by comparison to the results obtained in [6] at small M_∞ and by calculations on grids with different numbers of nodes. The period of characteristics change at β = 1.6, calculated by the equations for an incompressible fluid, was ${{t}_{0}} = 25.6$, and at ${{{\text{M}}}_{\infty }}$ = 0.1 the period was ${{t}_{0}} = 25.7$.

INTEGRALLY ASYMMETRIC FLOW AT TRANSONIC SPEEDS

Gas compressibility at transonic velocities strongly affects the limit of stable modes, the change period in flow characteristics, and the flow symmetry. The results below correspond to the parameters $\operatorname{Re}$ = 1000, $\Pr = 0.72$, k = 1.4, and η = 1.

As in the case of small M_∞, recirculation zones form on both sides of the plate. At the same time, these zones contract toward the surface of the plate with an increase in M_∞ and thus elongate, affecting the stability of the flow. So in the case of $\beta = 1.6$ at ${{{\text{M}}}_{\infty }} = 0$, the flow is periodical with ${{t}_{0}} = 25.6$; at ${{{\text{M}}}_{\infty }} = 0.6$, it is periodical with ${{t}_{0}} = 2.2$; and at ${{{\text{M}}}_{\infty }} = 0.9$, it is stable and symmetrical (Fig. 1). The decrease in the period of flow oscillations with an increase in M_∞ is due to the fact that at ${{{\text{M}}}_{\infty }} = 0$ recirculation zones are thick and the instability region covers the entire vortex region, and at ${{{\text{M}}}_{\infty }} = 0.6$ due to substantial contraction of these zones, the unstable flow region is located near the rear edge of the plate.

Fig. 1.

Vorticity contours from –49 to 49 with step 14 at ${{{\text{M}}}_{\infty }} = 0.9$, $\beta = 1.6$.

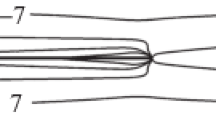
In the above cases, the integral of the lifting force over a period of time is zero for unstable flows, i.e., such flows can be called integrally symmetric. The evolution of the vorticity field during the second half of the period replicates the evolution during the first half, when the recirculation regions are mirrored across the plate surface and the vorticity sign changes. At $\beta \geqslant 3.2$ the flow loses its integral symmetry, starting from ${{{\text{M}}}_{\infty }} = 0.8$. The geometry of the vortex regions becomes substantially curved up (or down, the choice is random and depends on the process of reaching the periodic solution and on the type of perturbations), and the integral of the lifting force over the period ceases to be zero. Figure 2 shows the characteristic shape of recirculation areas at ${{{\text{M}}}_{\infty }} = 0.8$ and $\beta = 3.2$, and Fig. 3, the dependence of the lift coefficient c_y on time for this case. As can be seen from Fig. 3, the lifting force is negative in the smaller part of the period and positive in the larger part. With increasing M_∞ or β, coefficient c_y might stop changing sign over time, remaining either positive or negative all the time.

Fig. 2.

The same contours as in Fig. 1 at ${{{\text{M}}}_{\infty }} = 0.8$, $\beta = 3.2$.

Fig. 3.

Time dependence of the lift coefficient at ${{{\text{M}}}_{\infty }} = 0.8$, $\beta = 3.2$.

The existence of an integrally asymmetric solution implies another mirror solution. So, for the example in Fig. 3, a solution with a predominantly negative lift must exist. In order to show this, the following numerical experiment was conducted. A flow with ${{{\text{M}}}_{\infty }} = 0.9$ and $\beta = 4$ (Fig. 4) was studied. Over time, an integrally asymmetric flow with negative lift was established. Over a certain period of time, a strong perturbation was set as the lower boundary velocity increased up to $\beta = 8$. After some time, the velocity at the lower boundary became equal to $\beta = 4$ once again, but after that an integrally asymmetric flow with positive lifting force was established and the sign of the force did not change over time. The dashed lines in Fig. 4 show the average value of the lift coefficient before the change in the velocity of the plate surface and the same value with a different sign.

Fig. 4.

Sign switch of the lift coefficient after a strong flow disturbance at ${{{\text{M}}}_{\infty }} = 0.9$, $\beta = 4$.

CONCLUSIONS

A new type of nonstationary periodic flow with integral asymmetry of the flow characteristics over time is discovered. Such asymmetry is inherent in transonic velocities and sufficiently large β. In this case, large regions of supersonic flows appear in the flow, ending in shock waves. It is possible that the unsteady interaction of the shock waves with vortex regions is the cause of the integral asymmetry.