1. INTRODUCTION

Along with body and surface waves (a model example of the latter is the Rayleigh wave in a half-space), wedge waves comprise a fundamental type of oscillations of a solid and are intensively studied in geophysics (mountain ranges), machine building (edges of cutting tools), civil engineering (massive concrete buildings), etc. In this paper, we prove the existence of a symmetric mode in an elastic solid wedge for all allowable values of the Poisson ratio \(\sigma \in ( - 1,1{\text{/}}2)\) and openings close to π (both smaller and larger). Note that the presence of a wave localized in a vicinity of the edge of a wedge with an opening larger than a flat angle is a radically new effect, which has not been observed previously.

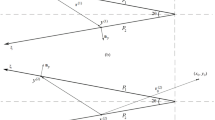
Let us consider a homogeneous isotropic solid wedge \({{K}^{\varepsilon }} = {{\Omega }^{\varepsilon }} \times \mathbb{R}\) with an opening close to a flat angle. Here (see Fig. 1),

$${{\Omega }^{\varepsilon }} = {\text{\{ }}({{x}_{1}},{{x}_{2}}){\text{:}}\,r > 0,\phi \in (\alpha ,\pi - \alpha ){\text{\} }},$$

ε = tanα is a small parameter and \(x = ({{x}_{1}},{{x}_{2}})\) and \((r,\phi )\) are, respectively, the Cartesian and polar coordinates.

Fig. 1.
figure 1

Wedge cross section.

Full size image

An elastic wave traveling along the edge of wedge \({{K}^{\varepsilon }}\) has the form

$${{U}^{\varepsilon }}({{x}_{1}},{{x}_{2}},{{x}_{3}},t) = {{u}^{\varepsilon }}({{x}_{1}},{{x}_{2}}){{e}^{{i(k{{x}_{3}} - \omega t)}}},$$
((1))

where t is time, k > 0 is the wave number, \(\omega = \omega (\varepsilon ) > 0\) is the frequency, and \({{u}^{\varepsilon }} = (u_{1}^{\varepsilon },u_{2}^{\varepsilon },u_{3}^{\varepsilon })\) is the vector function of displacements exponentially decaying at infinity.

Numerical experiments [4, 5] predicted the existence of a symmetric mode

$$\begin{gathered} u_{1}^{\varepsilon }( - {{x}_{1}},{{x}_{2}}) = - u_{1}^{\varepsilon }({{x}_{1}},{{x}_{2}}),\quad u_{2}^{\varepsilon }( - {{x}_{1}},{{x}_{2}}) = u_{2}^{\varepsilon }({{x}_{1}},{{x}_{2}}), \\ u_{3}^{\varepsilon }( - {{x}_{1}},{{x}_{2}}) = u_{3}^{\varepsilon }({{x}_{1}},{{x}_{2}}) \\ \end{gathered} $$
((2))

at all sufficiently small α > 0. These waves were investigated analytically at the physical level of rigor in [2, Ch. 10, §2; 9, 15]. Note also studies [6, 10], where symmetric modes were proven to exist for some ranges of wedge openings that are far from π.

2. STATEMENT OF THE PROBLEM

We eliminate variables \({{x}_{3}},t\) and reduce the Navier–Lamé system of equations and traction-free boundary conditions to the form

$$\begin{gathered} L({{\partial }_{1}},{{\partial }_{2}},{{\partial }_{3}}){{u}^{\varepsilon }} = {{\omega }^{2}}{{u}^{\varepsilon }}\quad {\text{in}}\quad {{\Omega }^{\varepsilon }}, \\ N({{\partial }_{1}},{{\partial }_{2}},{{\partial }_{3}}){{u}^{\varepsilon }} = 0\quad {\text{at}}\quad \partial {{\Omega }^{\varepsilon }}. \\ \end{gathered} $$
((3))

From here on, \({{\partial }_{1}} = \frac{\partial }{{\partial {{x}_{1}}}}\), \({{\partial }_{2}} = \frac{\partial }{{\partial {{x}_{2}}}}\), and \({{\partial }_{3}} = ik\). The components of the left-hand sides of (3) can be written as

$$\begin{gathered} \mathop {[L({{\partial }_{1}},{{\partial }_{2}},{{\partial }_{3}}){{u}^{\varepsilon }}]}\nolimits_n = - {{\partial }_{m}}\sigma _{{nm}}^{\varepsilon }, \\ \mathop {[N({{\partial }_{1}},{{\partial }_{2}},{{\partial }_{3}}){{u}^{\varepsilon }}]}\nolimits_n = \sigma _{{nm}}^{\varepsilon }{{\nu }_{m}},\quad n = 1,2,3, \\ \end{gathered} $$

\(\nu = ({{\nu }_{1}},{{\nu }_{2}},0)\) is the unit vector of the outward normal to the wedge boundary, and the stress-tensor components \(\sigma _{{nm}}^{\varepsilon }\) are determined by the formulas

$$\sigma _{{nm}}^{\varepsilon } \equiv {{\sigma }_{{nm}}}[{{u}^{\varepsilon }}] = \lambda {{\partial }_{l}}u_{l}^{\varepsilon }{{\delta }_{{n,m}}} + \mu ({{\partial }_{m}}u_{n}^{\varepsilon } + {{\partial }_{n}}u_{m}^{\varepsilon }),$$

where \(\lambda \) and \(\mu \) are the Lamé constants, \(\lambda + \frac{2}{3}\mu > 0\), \(\mu > 0\), and \({{\delta }_{{n,m}}}\) is the Kronecker delta. Identical subscripts suggest summation from 1 to 3.

We consider in detail the case of \(\varepsilon > 0\). For \(\varepsilon < 0\) (i.e., for wedge openings larger than π), all calculations remained the same and only Figs. 1 and 2 change.

Fig. 2.
figure 2

Half-plane with a cut.

Full size image

Similarly to [12], we transform \({{\Omega }^{\varepsilon }}\) into a half-plane with a cut of opening \(2\alpha \) (see Fig. 2)

$${{\Pi }^{\varepsilon }} = \{ ({{x}_{1}},{{x}_{2}}) \in {{\mathbb{R}}^{2}}{\text{:}}\,{{x}_{2}} > 0,{\text{|}}{{x}_{1}}{\text{|}} > \varepsilon {{x}_{2}}\} .$$

The equations and boundary condition (3) are rewritten as

$$\begin{gathered} L({{\partial }_{1}},{{\partial }_{2}},{{\partial }_{3}}){{u}^{\varepsilon }} = {{\omega }^{2}}{{u}^{\varepsilon }}\quad {\text{in}}\quad {{\Pi }^{\varepsilon }}; \\ \sigma _{{n2}}^{\varepsilon } = 0\quad {\text{at}}\quad {{x}_{2}} = 0, \\ \end{gathered} $$
((4))

and they are supplemented with the transmission conditions at the angular cut sides:

$$\begin{gathered} u_{n}^{\varepsilon }(\varepsilon {{x}_{2}},{{x}_{2}})\nu _{n}^{{\varepsilon + }} + u_{n}^{\varepsilon }( - \varepsilon {{x}_{2}},{{x}_{2}})\nu _{n}^{{\varepsilon - }} = 0; \\ u_{3}^{\varepsilon }(\varepsilon {{x}_{2}},{{x}_{2}}) = u_{3}^{\varepsilon }( - \varepsilon {{x}_{2}},{{x}_{2}}); \\ \end{gathered} $$
((5))
$$u_{n}^{\varepsilon }(\varepsilon {{x}_{2}},{{x}_{2}})\tau _{n}^{{\varepsilon + }} + u_{n}^{\varepsilon }( - \varepsilon {{x}_{2}},{{x}_{2}})\tau _{n}^{{\varepsilon - }} = 0\quad {\text{for}}\quad {{x}_{2}} > 0;$$
$$\sigma _{{nm}}^{\varepsilon }(\varepsilon {{x}_{2}},{{x}_{2}})\nu _{m}^{{\varepsilon + }}\, + \,\sigma _{{nm}}^{\varepsilon }( - \varepsilon {{x}_{2}},{{x}_{2}})\nu _{m}^{{\varepsilon - }}\, = \,0\,\,\,{\text{for}}\,\,\,{{x}_{2}}\, > \,0,$$
((6))

where \({{\nu }^{{\varepsilon \pm }}}\, = \,{{(1\, + \,{{\varepsilon }^{2}})}^{{ - 1/2}}}( \mp 1,\varepsilon ,0)\) and τε± = (1 + \({{\varepsilon }^{2}}{{)}^{{ - 1/2}}}( - \varepsilon , \mp 1,0)\) are the normal and tangent vectors, respectively.

The generalized statement of problem (4)–(6) corresponds to the integral identity

$$\begin{gathered} {{a}^{\varepsilon }}(ik;{{u}^{\varepsilon }},{v}) \equiv \int\limits_{{{\Pi }^{\varepsilon }}}^{} {\sigma _{{nm}}^{\varepsilon }} \overline {{{\partial }_{m}}{{{v}}_{n}}} dx = {{\omega }^{2}}\int\limits_{{{\Pi }^{\varepsilon }}}^{} {u_{n}^{\varepsilon }} \overline {{{{v}}_{n}}} dx, \\ {v} \in H_{\sharp }^{1}({{\Pi }^{\varepsilon }}), \\ \end{gathered} $$
((7))

where \(H_{\sharp }^{1}({{\Pi }^{\varepsilon }})\) is the space of vector functions from \({{H}^{1}}({{\Pi }^{\varepsilon }})\) that satisfy condition (5). Since \({{a}^{\varepsilon }}(ik;u,u)\) is the closed positive quadratic form in \(H_{\sharp }^{1}({{\Pi }^{\varepsilon }})\), the positive self-adjoint operator \({{\mathcal{A}}^{\varepsilon }}(ik)\) in the space of vector functions \({{L}_{2}}({{\Pi }^{\varepsilon }})\) is put into correspondence with problem (7) [1, Ch. 10]. It was proven in [7] that the essential spectrum of operator \({{\mathcal{A}}^{\varepsilon }}(ik)\) coincides with ray \([c_{R}^{2}{{k}^{2}}, + \infty )\), where cR is the Rayleigh wave velocity. Therefore, only the discrete spectrum of problem (4)–(6) can be located below the cutoff point \(\omega _{R}^{2} = c_{R}^{2}{{k}^{2}}\), the nonemptiness of which provides the existence of wave (1) localized in a vicinity of the wedge edge and propagating along the edge with a velocity below cR.

3. ASYMPTOTIC EXPANSIONS

The eigenvalue of problem (4)–(6) will be sought in the form

$$\Lambda (\varepsilon ) = \omega _{R}^{2} - {{\varepsilon }^{2}}{{\Lambda }^{1}} + \tilde {\Lambda }(\varepsilon ),\quad {{\Lambda }^{1}} > 0,$$
((8))

where \({{\Lambda }^{1}}\) is to be determined and \(\tilde {\Lambda }(\varepsilon )\) is a small residue. We apply the method of matched asymptotic expansions and choose the following ansatz for the “inner” (applicable in a finite vicinity of the cut) expansion of the corresponding vector eigenfunction \({{u}^{\varepsilon }}\):

$${{u}^{\varepsilon }} = {{w}^{0}} + \varepsilon {{w}^{1}} + {{\varepsilon }^{2}}{{w}^{2}} + \ldots \,.$$
((9))

Here, dots substitute for minor asymptotic terms and w0 is the Rayleigh wave

$${{u}^{R}}({{x}_{2}}) = (0,u_{2}^{R}(k{{x}_{2}}),u_{3}^{R}(k{{x}_{2}})),$$
((10))
$$\begin{gathered} u_{2}^{R}({{x}_{2}}) = {{\kappa }_{l}}{{e}^{{ - {{\kappa }_{l}}{{x}_{2}}}}} - \frac{{2{{\kappa }_{l}}}}{{1 + \kappa _{t}^{2}}}{{e}^{{ - {{\kappa }_{t}}{{x}_{2}}}}}, \\ u_{3}^{R}({{x}_{2}}) = - {{e}^{{ - {{\kappa }_{l}}{{x}_{2}}}}} + \frac{{1 + \kappa _{t}^{2}}}{2}{{e}^{{ - {{\kappa }_{t}}{{x}_{2}}}}}. \\ \end{gathered} $$
((11))

Here \(\kappa _{t}^{2} = 1 - c_{R}^{2}{\text{/}}c_{t}^{2} > 0\), \(\kappa _{l}^{2} = 1 - c_{R}^{2}{\text{/}}c_{l}^{2} > 0\), and ct and cl are the velocities of the transverse and longitudinal body waves, respectively.

Vector function w0 satisfies the equations and boundary conditions (4) with \({{\omega }^{2}} = \omega _{R}^{2}\) but retains the residuals in the transmission conditions (5) and (6). The major (of order ε) parts of these residuals are compensated by a solution to the problem

$$\begin{gathered} L({{\partial }_{1}},{{\partial }_{2}},{{\partial }_{3}}){{w}^{1}} = \omega _{R}^{2}{{w}^{1}}\quad {\text{in}}\quad {{\Pi }^{0}}, \\ N({{\partial }_{1}},{{\partial }_{2}},{{\partial }_{3}}){{w}^{1}} = 0,\quad {{x}_{2}} = 0; \\ \end{gathered} $$
((12))
$$ - w_{n}^{1}( + 0,{{x}_{2}}) + w_{n}^{1}( - 0,{{x}_{2}}) = - 2u_{2}^{R}({{x}_{2}}){{\delta }_{{n,1}}};$$
$$\begin{gathered} - {{\sigma }_{{n1}}}[{{w}^{1}}]( + 0,{{x}_{2}}) + {{\sigma }_{{n1}}}[{{w}^{1}}]( - 0,{{x}_{2}}) \\ = - 2{{\sigma }_{{n2}}}[{{u}^{R}}](0,{{x}_{2}}),\quad {{x}_{2}} > 0. \\ \end{gathered} $$
((13))

Any solution to the problem (12)–(13), which grows no faster than the power law at \({{x}_{1}} \to \pm \infty \), has the form

$${{w}^{1}}(x) = \sum\limits_ \pm \,{{\chi }_{ \pm }}({{x}_{1}})(c_{u}^{ \pm }{{u}^{R}}(x) + c_{{v}}^{ \pm }{{{v}}^{R}}(x)) + {{\tilde {w}}^{1}}(x),$$
((14))

where \({{\chi }_{ \pm }}\) are the smooth cut-off functions, \({{\chi }_{ \pm }}({{x}_{1}}) = 1\) for \( \pm {{x}_{1}} > 2\) and \({{\chi }_{ \pm }}({{x}_{1}}) = 0\) for \( \pm {{x}_{1}} < 1\), and the residual term \({{\tilde {w}}^{1}}(x)\) decays exponentially at \({{x}_{1}} \to \pm \infty \) and \({{x}_{2}} \to + \infty \). Finally, \({{{v}}^{R}}\) is the solution to problem (3) in \({{\Omega }^{0}}\), which linearly grows with x1 [8]:

$${{{v}}^{R}}({{x}_{1}},{{x}_{2}}) = ( - i{{k}^{{ - 1}}}u_{3}^{R}(k{{x}_{2}}),{{x}_{1}}u_{2}^{R}(k{{x}_{2}}),{{x}_{1}}u_{3}^{R}(k{{x}_{2}})).$$

Coefficients \(c_{u}^{ \pm }\) and \(c_{{v}}^{ \pm }\) in (14) are determined not uniquely, because a linear combination \({{C}_{u}}{{u}^{R}}\, + \,{{C}_{{v}}}{{{v}}^{R}}\) is a solution to the homogeneous problem (12)–(13). Therefore, we assume that \(c_{u}^{ + } + c_{u}^{ - } = 0\) and \(c_{{v}}^{ + } + c_{{v}}^{ - } = 0\). We apply Green’s formula in rectangle \(\{ x{\text{:}}\,{\text{|}}{{x}_{1}}{\text{|}} < T,0 < {{x}_{2}} < T{\text{\} }}\) to the functions \({{w}^{1}}\) and \({{u}^{R}}\) and let T tend to \( + \infty \); as a result,

$$2c_{{v}}^{ + } = \frac{{2\int\limits_0^{ + \infty } {({{\sigma }_{{22}}}[{{u}^{R}}]\overline {u_{2}^{R}} + {{\sigma }_{{32}}}[{{u}^{R}}]\overline {u_{3}^{R}} - u_{2}^{R}\overline {{{\sigma }_{{11}}}[{{u}^{R}}]} )} d{{x}_{2}}}}{{\int\limits_0^{ + \infty } {({{\sigma }_{{21}}}[{{{v}}^{R}}]\overline {u_{2}^{R}} + {{\sigma }_{{31}}}[{{{v}}^{R}}]\overline {u_{3}^{R}} - {v}_{1}^{R}\overline {{{\sigma }_{{11}}}[{{u}^{R}}]} )} d{{x}_{2}}}}.$$

Hence, using (11), we arrive at

$$c_{{v}}^{ + }\, = \, - \,\frac{{B{{{(1\, - \,B)}}^{{1/2}}}(4\, - \,B){{{(2\, - \,B)}}^{2}}(16\, - \,24B\, + \,8{{B}^{2}}\, - \,{{B}^{3}})}}{{({{{(4 - B)}}^{2}} - 8)({{{(1 - B)}}^{2}}(7 - 2B) + 1){{{(3 - B)}}^{4}}}},$$
((15))

where \(B = 1 - \kappa _{t}^{2} \in (0,1)\). Similar calculations show that \(c_{u}^{ + } = 0\). Thus, the first correction to (9) is constructed. The next terms of the expansion can also be found; however, their explicit formulas are not required.

Note that \(c_{{v}}^{ + } < 0\) because, due to the Rayleigh equation [14],

$$16 - 24B + 8{{B}^{2}} - {{B}^{3}} = 16(1 - B)c_{t}^{2}c_{l}^{{ - 2}} > 0.$$
((16))

To construct the “outer” asymptotic expansion \({{u}^{\varepsilon }}\) (at large \({\text{|}}{{x}_{1}}{\text{|}}\) values), we consider the vector functions

$${{W}^{{\varepsilon \pm }}}({{x}_{1}},{{x}_{2}}) = {{e}^{{\xi _{ \pm }^{\varepsilon }{{x}_{1}}}}}{{U}^{{\varepsilon \pm }}}({{x}_{2}}),\quad \pm \xi _{ \pm }^{\varepsilon } < 0,$$

describing the waves that exponentially decay at \({{x}_{1}} \to \pm \infty \). They should be solutions to problem (3) in \({{\Omega }_{0}}\) with the spectral parameter \({{\omega }^{2}} = \Lambda (\varepsilon )\). Therefore, \({{U}^{{\varepsilon \pm }}}\) are solutions to the boundary-value problem for the system of ordinary differential equations

$$\begin{gathered} L(\xi _{ \pm }^{\varepsilon },{{\partial }_{2}},ik){{U}^{{\varepsilon \pm }}}({{x}_{2}}) = {{\omega }^{2}}{{U}^{{\varepsilon \pm }}}({{x}_{2}}),\quad {{x}_{2}} > 0; \\ N(\xi _{ \pm }^{\varepsilon },{{\partial }_{2}},ik){{U}^{{\varepsilon \pm }}}(0) = 0. \\ \end{gathered} $$
((17))

To solve (17), we use the standard asymptotic ansatz (see [3, Ch. 9])

$$\begin{gathered} \xi _{ \pm }^{\varepsilon } = \mp \varepsilon {{\xi }^{1}} + \mathop {\tilde {\xi }}\nolimits_ \pm ^\varepsilon ,\quad {{\xi }^{1}} > 0; \\ {{U}^{{\varepsilon \pm }}}({{x}_{2}}) = {{U}^{0}}({{x}_{2}}) + \xi _{ \pm }^{\varepsilon }{{U}^{1}}({{x}_{2}}) + \mathop {\tilde {U}}\nolimits^{\varepsilon \pm } ({{x}_{2}}). \\ \end{gathered} $$

For the first two terms of the expansion, we derive the problems

$$\begin{gathered} L(0,{{\partial }_{2}},ik){{U}^{0}}({{x}_{2}}) - \omega _{R}^{2}{{U}^{0}}({{x}_{2}}) = 0,\quad {{x}_{2}} > 0; \\ N(0,{{\partial }_{2}},ik){{U}^{0}}(0) = 0 \\ \end{gathered} $$

and

$$\begin{gathered} L(0,{{\partial }_{2}},ik){{U}^{1}}({{x}_{2}}) - \omega _{R}^{2}{{U}^{1}}({{x}_{2}}) = - {{\partial }_{\xi }}L(0,{{\partial }_{2}},ik){{U}^{0}}({{x}_{2}}), \\ {{x}_{2}} > 0; \\ N(0,{{\partial }_{2}},ik){{U}^{1}}(0) = - {{\partial }_{\xi }}N(0,{{\partial }_{2}},ik){{U}^{0}}(0), \\ \end{gathered} $$

the solutions to which are

$${{U}^{0}}({{x}_{2}}) = {{u}^{R}}({{x}_{2}}),\quad {{U}^{1}}({{x}_{2}}) = ( - i{{k}^{{ - 1}}}u_{3}^{R}(k{{x}_{2}}),0,0).$$
((18))

The next term should be sought from the problem

$$\begin{gathered} L(0,{{\partial }_{2}},ik){{U}^{2}}({{x}_{2}}) - \omega _{R}^{2}{{U}^{2}}({{x}_{2}}) \\ = - {{({{\xi }^{1}})}^{2}}({{\partial }_{\xi }}L(0,{{\partial }_{2}},ik){{U}^{1}}({{x}_{2}}) \\ + \frac{1}{2}\partial _{\xi }^{2}L(0,{{\partial }_{2}},ik){{U}^{0}}({{x}_{2}})) - {{\Lambda }^{1}}{{U}^{0}}({{x}_{2}}),\quad {{x}_{2}} > 0; \\ N(0,{{\partial }_{2}},ik){{U}^{2}}(0) = - {{({{\xi }^{1}})}^{2}}{{\partial }_{\xi }}N(0,{{\partial }_{2}},ik){{U}^{1}}(0). \\ \end{gathered} $$

Its solvability condition

$$b{{({{\xi }^{1}})}^{2}} + {{\Lambda }^{1}}{\text{||}}{{U}^{0}};{{L}^{2}}({{\mathbb{R}}_{ + }}){\text{|}}{{{\text{|}}}^{2}} = 0$$
((19))

includes the coefficient

$$\begin{gathered} b = \int\limits_0^{ + \infty } {\left( {i\frac{{(\lambda \, + \,\mu )}}{k}u_{3}^{{R'}}\overline {u_{2}^{R}} \, - \,(\lambda \, + \,\mu ){\text{|}}u_{3}^{R}{{{\text{|}}}^{2}}\, - \,\mu {\text{|}}u_{2}^{R}{{{\text{|}}}^{2}}\, - \,\mu {\text{|}}u_{3}^{R}{{{\text{|}}}^{2}}} \right)d{{x}_{2}}} \\ \, + i\frac{\lambda }{k}u_{3}^{R}(0)\overline {u_{2}^{R}(0)} \\ = - \frac{{{{B}^{3}}(16\, - \,24B\, + \,8{{B}^{2}}\, - \,{{B}^{3}})({{{(1 - B)}}^{2}}(7 - 2B) + 1)}}{{128k{{{(1 - B)}}^{{5/2}}}{{{(2 - B)}}^{2}}}}\, < \,0. \\ \end{gathered} $$
((20))

Here, relations (11) and (16) were taken into account. Thus, quadratic equation (19) has two real roots \( \pm {{\xi }^{1}}\). The estimate of the residue \({\text{|}}\mathop {\tilde {\xi }}\nolimits_ \pm ^\varepsilon {\text{|}} \leqslant c{{\varepsilon }^{2}}\) is ensured by the general results [3, Ch. 9].

The outer asymptotic expansions at \( \pm {{x}_{1}} \to + \infty \) are sought in the form

$$\begin{gathered} (1 + \varepsilon C_{ \pm }^{1} + \ldots ){{W}^{{\varepsilon \pm }}}(x) + \ldots = {{U}^{0}}({{x}_{2}}) \\ \, + \varepsilon ( \mp {{\xi }^{1}}({{U}^{1}}({{x}_{2}}) + {{x}_{1}}{{U}^{0}}({{x}_{2}})) + C_{ \pm }^{1}{{U}^{0}}({{x}_{2}})) + \ldots . \\ \end{gathered} $$
((21))

To match the asymptotic expansions (see [11]), we equate the coefficients at identical powers of \(\varepsilon \) in (9) and (21). Due to (18), the main terms comprise the Rayleigh wave (10): \({{w}^{0}} = {{U}^{0}} = {{u}^{R}}\). According to (14), the coincidence of the terms on the order of \(\varepsilon \) yields

$${{\xi }^{1}} = - c_{v}^{ + },\quad C_{ \pm }^{1} = c_{u}^{ \pm } = 0.$$
((22))

Relation (22) is valid due to the above-verified inequality \(c_{{v}}^{ + } < 0\). From (19) and (15), we derive the final formula for the correction term in expansion (8):

$${{\Lambda }^{1}} = \frac{{{{{(c_{{v}}^{ + })}}^{2}}{\text{|}}b{\text{|}}}}{{{\text{||}}{{U}^{0}};{{L}^{2}}({{\mathbb{R}}_{ + }}){\text{|}}{{{\text{|}}}^{2}}}} > 0.$$

Note that, due to (15), (20), and

$${\text{||}}{{U}^{0}};{{L}^{2}}({{\mathbb{R}}_{ + }}{\text{)|}}{{{\text{|}}}^{2}} = \frac{{{{B}^{2}}({{{(1 - B)}}^{2}}(7 - 2B) + 1)}}{{8k{{{(1 - B)}}^{{\frac{3}{2}}}}{{{(2 - B)}}^{2}}}},$$

the \({{\Lambda }^{1}}\) value is independent of the wave number \(k\).

The estimate of the asymptotic residue \({\text{|}}\tilde {\Lambda }(\varepsilon ){\text{|}} \leqslant c{{\varepsilon }^{3}}\) in representation (8) of the eigenvalue \(\Lambda (\varepsilon ) = {{\omega }^{2}}(\varepsilon )\) of problem (4)–(6) in \({{\Pi }^{\varepsilon }}\) (and, therefore, problem (3) in \({{\Omega }^{\varepsilon }}\)) is derived according to the standard scheme (compare [11] and [13]) based on the spectral expansion of the resolvent of operator \({{\mathcal{A}}^{\varepsilon }}(ik)\) of problem (7) (see [1, Ch. 6]); notably, the test vector function is constructed from the found terms of the inner (9) and outer (21) expansions using an appropriate partition of unity.

Since the Rayleigh wave (the first approximation in asymptotic expansions (9) and (21)) is symmetric, it is clear that all the following terms of the expansions also have symmetry (2). Thus, the constructed mode is symmetric. Note once again that all calculations are independent of the sign of ε; therefore, the symmetric wave exists at wedge openings both smaller and larger than the flat angle.

ACKNOWLEDGMENTS

This study was supported by the Russian Science Foundation, grant no. 17-11-01003.