The approximation of the Earth’s physical surface by a mathematical surface is commonly carried out by a sphere or an ellipsoid of revolution. A triaxial ellipsoid can be used in some cases. Geodetic heights of points of the Earth’s surface are commonly calculated by approximate methods using the relation between spatial rectangular coordinates x, y, z and geodetic coordinates B, L, H. All calculations use the assumption of small flattening values or eccentricity of an ellipse the rotation of which generates an ellipsoid. Meanwhile, the shape of some small Solar System bodies is far from being spherical, so this assumption is not correct. The triaxial ellipsoid is used for approximation of such bodies. Due to hard determination of the geodesic height relative to the triaxial ellipsoid or the ellipsoid of revolution with a large polar flattening, some authors suggest using the geodetic height relative to the sphere [7]. For the hypsometric map of Phobos, the satellite of Mars, in the Atlas of the Terrestrial Planets [1], the surface of the triaxial ellipsoid was taken as a level surface and the heights were determined by the radius vector taken from the digital elevation model. It is also recommended [3] to use the triaxial ellipsoid as an approximation surface for Phobos and to specify the parameters of this ellipsoid.

The iteration method [4] was developed to determine the geodetic height relative to the triaxial ellipsoid. As the first approximation, the authors propose to choose either a zero value of height H or the length difference of the radius vector to the reference point and the radius vector to the point of crossing with the ellipsoid. The method was tested in development of the Phobos Atlas maps [2]. Meanwhile, such first approximation variants are incorrect for small bodies of the Solar system, for example, the Asteroid 433 Eros.

The proposed fundamentally new approach to calculation of the geodesic height relative to the triaxial ellipsoid is based on the joint use of the equation of the normal to the surface, passing through a given point, and the surface equation proper. The method is reduced to solving the sixth-degree equation by the Sturm method [6] and the fourth-degree equation by the Ferrari method [5].

A geodetic height, i.e., the shortest distance from a physical surface point of a celestial body \(({{x}_{0}},{{y}_{0}},{{z}_{0}})\) to its approximating surface is specified by a straight line segment that is perpendicular to this surface and passes through the point \((x,y,z)\). The line perpendicular to the mathematical surface \(f(x,y,z) = C\) and passing through the point with coordinates \(({{x}_{0}},{{y}_{0}},{{z}_{0}})\) is specified by the following equations:

$$\frac{{{{x}_{0}} - x}}{{\frac{{\partial f(x,y,z)}}{{\partial x}}}} = \frac{{{{y}_{0}} - y}}{{\frac{{\partial f(x,y,z)}}{{\partial y}}}} = \frac{{{{z}_{0}} - z}}{{\frac{{\partial f(x,y,z)}}{{\partial z}}}}.$$

The distance between the points with coordinates \(({{x}_{0}},{{y}_{0}},{{z}_{0}})\) and \((x,y,z)\) is as follows:

$$h = \sqrt {{{{({{x}_{0}} - x)}}^{2}} + {{{({{y}_{0}} - y)}}^{2}} + {{{({{z}_{0}} - z)}}^{2}}} .$$
((1))

If \(f(x,y,z) = C\) is a triaxial ellipsoid with semi-axes a, b, c, the surface point with coordinates \((x,y,z)\) can be calculated by the following system of equations:

$$\begin{gathered} \frac{{{{x}_{0}} - x}}{{\frac{x}{{{{a}^{2}}}}}} = \frac{{{{y}_{0}} - y}}{{\frac{y}{{{{b}^{2}}}}}}, \\ \frac{{{{x}_{0}} - x}}{{\frac{x}{{{{a}^{2}}}}}} = \frac{{{{z}_{0}} - z}}{{\frac{z}{{{{c}^{2}}}}}}, \\ \frac{{{{x}^{2}}}}{{{{a}^{2}}}} + \frac{{{{y}^{2}}}}{{{{b}^{2}}}} + \frac{{{{z}^{2}}}}{{{{c}^{2}}}} = 1. \\ \end{gathered} $$
((2))

Expression of y and z through x from the first two equations, on the basis of the third equation, yields a sixth-degree equation relative to x. Meanwhile, a considerable difference in semi-axes values can result in too wide a spread in the coefficients of this equation, which, in turn, can lead to a lower calculation accuracy. To avoid this problem, the following substitution is made:

$${{x}_{0}} = a{{x}_{{0n}}},\quad {{y}_{0}} = b{{y}_{{0n}}},\quad {{z}_{0}} = c{{z}_{{0n}}},$$
$$x = a{{x}_{n}},\quad y = b{{y}_{n}},\quad z = c{{z}_{n}}.$$

Then, the system of equations (2) will take the following form:

$$\begin{gathered} \frac{{{{x}_{{0n}}} - {{x}_{n}}}}{{{{x}_{n}}}} = \frac{{(1 - e_{1}^{2})({{y}_{{0n}}} - {{y}_{n}})}}{{{{y}_{n}}}}, \\ \frac{{{{x}_{{0n}}} - {{x}_{n}}}}{{{{x}_{n}}}} = \frac{{(1 - {{e}^{2}})({{z}_{{0n}}} - {{z}_{n}})}}{{{{z}_{n}}}}, \\ x_{n}^{2} + y_{n}^{2} + z_{n}^{2} = 1, \\ \end{gathered} $$
((3))

where \(e_{1}^{2}\) and \({{e}^{2}}\) are the squared eccentricities of the equatorial ellipse and the section ellipse of the initial meridian.

Accordingly, we obtain a sixth-degree equation relative to \({{x}_{n}}\):

$${{a}_{0}}x_{n}^{6} + {{a}_{1}}x_{n}^{5} + {{a}_{2}}x_{n}^{4} + {{a}_{3}}x_{n}^{3} + {{a}_{4}}x_{n}^{2} + {{a}_{5}}{{x}_{n}} + {{a}_{6}} = 0.$$
((4))

The coefficients of this equation are as follows:

$${{a}_{0}} = e_{1}^{4}{{e}^{4}},\quad {{a}_{1}} = - 2{{x}_{{0n}}}(e_{1}^{2} + {{e}^{2}})e_{1}^{2}{{e}^{2}},$$
$$\begin{gathered} {{a}_{2}} = x_{{0n}}^{2}[{{(e_{1}^{2} + {{e}^{2}})}^{2}} + 2e_{1}^{2}{{e}^{2}}] + y_{{0n}}^{2}{{e}^{4}}{{(1 - e_{1}^{2})}^{2}} \\ + \;z_{{0n}}^{2}e_{1}^{4}{{(1 - {{e}^{2}})}^{2}} - e_{1}^{4}{{e}^{4}}, \\ \end{gathered} $$
$$\begin{gathered} {{a}_{3}} = 2{{x}_{{0n}}}[(e_{1}^{2} + {{e}^{2}})(e_{1}^{2}{{e}^{2}} - x_{{0n}}^{2}) \\ - \;y_{{0n}}^{2}{{e}^{2}}{{(1 - e_{1}^{2})}^{2}} - z_{{0n}}^{2}e_{1}^{2}{{(1 - {{e}^{2}})}^{2}}], \\ \end{gathered} $$
$$\begin{gathered} {{a}_{4}} = x_{{0n}}^{2}[x_{{0n}}^{2} + y_{{0n}}^{2}{{(1 - e_{1}^{2})}^{2}} + z_{{0n}}^{2}{{(1 - {{e}^{2}})}^{2}} \\ - \;{{(e_{1}^{2} + {{e}^{2}})}^{2}} - 2e_{1}^{2}{{e}^{2}}], \\ \end{gathered} $$
$${{a}_{5}} = 2x_{{0n}}^{3}(e_{1}^{2} + {{e}^{2}}),\quad {{a}_{6}} = - x_{{0n}}^{4}.$$

It should be noted that in the case when the point \(({{x}_{0}},{{y}_{0}},{{z}_{0}})\) lies in one of the coordinate planes or when the mathematical surface is an ellipsoid of revolution, Eq. (4) passes into a fourth-degree equation.

In solving Eq. (4), the first two roots \({{x}_{{1n}}}\), \({{x}_{{2n}}}\) can be calculated with the help of the Sturm chain, while other roots can be determined by the Ferrari method. The root for which a distance h is minimum is chosen from the calculated values. The planetocentric latitude and longitude of the surface point with coordinates \((x,y,z)\) are obtained from the known formulas:

$$x = r\cos \varphi \cos \lambda ,\quad y = r\cos \varphi \sin \lambda ,\quad z = r\sin \varphi .$$

The JavaScript software developed to calculate heights has been placed on the website of the Center for Geoinformational Studies, Institute of Geography, Russian Academy of Sciences [8]. The program code can be viewed and copied. The input data include the planetocentric longitude and latitude of the physical surface point and the length of the radius vector to this point. At the output, the values of new latitudes, longitudes, and heights are added to this table.

To confirm the theoretical studies, hypsometric maps were compiled for the Asteroid 433 Eros according to the digital model NLR190 data [9]. In the mapping process, the calculated height is referred to the aforementioned angular coordinates. It should be noted that the geodetic latitude of the points with coordinates \({{x}_{0}},{{y}_{0}},{{z}_{0}}\) and \(x,y,z\) is the same.

The procedure considered for determination of the geodetic heights provides the possibility of analyzing the proposed mathematical surface in order to compile map of relief. Considerable deviations of the body’s physical surface from an ellipsoid can be caused by both high fluctuations in heights and by unsuccessfully selected parameters of the ellipsoid, including its orientation relative to the body. It should be noted that on the Phobos hypsometric map in the Atlas of Terrestrial Planets [1], the thematic content is given without taking into account the hypsometry of local relief features. In the Phobos Atlas [2], contours are superimposed on the photo mosaic, but they are not always coincide with local relief features.

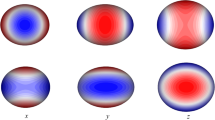
Figure 1 shows the Asteroid 433 Eros hypsometric map in an equidistant along meridians cylindrical projection of a triaxial ellipsoid with semi-axes 17 000 m, 5500 m, and 5500 m, recommended by the International Astronomical Union. It follows from comparison with the photo map (Fig. 2) that in the meridian of 0, 360° there is an elevation difference area that is not coincide with the actual relief. The use of an ellipsoid with parameters of 14 000 m, 5500 m, and 5500 m makes it possible to display more adequately the terrains in this area (Fig. 3).

Fig. 1.
figure 1

Hypsometric map of the Asteroid 433 Eros for the triaxial ellipsoid with semi-axes 17 000 m, 5500 m, and 5500 m.

Full size image
Fig. 2.
figure 2

Photo map of the Asteroid 433 Eros for the triaxial ellipsoid with semi-axes 17 000 m, 5500 m, and 5500 m.

Full size image
Fig. 3.
figure 3

Hypsometric map of the Asteroid 433 Eros for a triaxial ellipsoid with semi-axes 14 000 m, 5500 m, and 5500 m.

Full size image

Hence, we propose accurate calculation of the geodetic heights of the celestial body’s surface points relative to the triaxial ellipsoid with arbitrary flattening. The method developed was tested by the example of the Asteroid 433 Eros, and it can be applied to other bodies. By analogy with the Earth, for which different ellipsoids of revolution are used, it is proposed to use different reference ellipsoids for better approximation of different areas.