INTRODUCTION

The study of self-focusing and filamentation of femtosecond laser pulses is among promising directions of research in modern nonlinear optics. These phenomena occur due to spatial and temporal modulations of the optical field phase and amplitude; they lead to the formation of nonlinear foci and plasma channels with the free electron density ρе > 1020 m−3, the generation of supercontinuum luminescence, conical emission, and terahertz radiation. Fundamental results obtained in the studies of self-focusing and filamentation of laser pulses [1, 2] are used in solution of many scientific problems and development of new engineering processes.

It is known that the group velocity dispersion (GVD) of pulses can strongly affect the self-focusing and filamentation of laser radiation in some cases [3]. Most of the studies are focused on the processes occurring in condensed media (K8 glass [4], fused silica [5]). When using femtosecond lasers in the study of the atmosphere in the visible and near-IR wavelength regions, including light energy transmission and laser ranging and communication, the effect of normal dispersion on laser pulse parameters becomes a problem. The problem is much more complicated in the case of high-power laser radiation, which produces self-action of laser pulses in the atmosphere.

The dispersion counteraction to pulse collapse is one of the important results which show the role of dispersion in self-focusing. The self-focusing power threshold increases with enhancement of dispersion distortions [6, 7]. In [8], in a Kerr medium at normal GVD, the threshold was assessed at different diffraction and dispersion lengths. The importance of the power level for estimation of the role of GVD was especially noted in [3], since the air dispersion can cease radiation self-focusing at relatively low powers (a little higher than critical). Indeed, during self-focusing of pulses of a specified power, the dispersion length can be of a minimal scale among the characteristic longitudinal lengths for millimeter laser beams [9, 10]. This results in a drop in the peak power and, thus, violation of the self-focusing conditions. In this connection, it is of interest to consider this effect in more detail and for a wider set of input pulse parameters. It is necessary to find out what are the main physical causes of the dispersion effect on the self-focusing and filamentation of laser pulses; can the GVD affect nonlinear processes under conditions where the characteristic longitudinal scale of its manifestation is greater than the length of the region where the strongest nonlinear pulse transformations occur?

Due to the development of the diffraction-beam approach [11], which has proven to be an effective tool for the analysis of the filamentation of high-power laser pulses [12, 13], it becomes possible to answer the above questions. In particular, it is important to trace the redistribution of energy between different time layers of a laser pulse, to derive relations which provide for approximate estimates of the dispersion effect to forecasting the femtosecond laser pulse propagation through the atmosphere.

In this work, self-focusing and filamentation of laser pulses in air were simulated using a numerical solution of the equation for slowly varying complex amplitude of an electric field (nonlinear Schrödinger equation) [1]. The mathematical statement of the problem is described in [11]. The calculations were performed for pulses of a Ti:sapphire laser with the length tp = 100 and 20 fs at the central wavelength λ = 800 nm. Laser beams with the initial radius R0 (in terms of the intensity decay level e–1) from 0.18 to 3 mm and the relative peak power η from 3 to 9 were considered, which corresponds to the single filamentation mode. Here, η determines the ratio of the peak power P0 to the self-focusing critical power of a collimated Gaussian beam Рсr = 3.18 GW for the parameters specified [9].

MAIN RELATIONS USED WITHIN THE DIFFRACTION-BEAM TUBE APPROACH

Let us write the initial relationships of diffraction-beam optics, which follow from the amplitude-phase approach [11] based on the transition from the complex amplitude U(x, y, z; t) of the electric field of a light wave, which is connected with the field strength as

to the real wave amplitude А(x, y, z; t) and phase φ(x, y, z; t):

$$U = A{{e}^{{i\varphi }}},$$

where x and y are the coordinates of the transverse vector r⊥; z is the longitudinal coordinate; t is the time; and ω0 and k0 are the central frequency and wavenumber of the laser radiation. Equations for А and φ are connected with each other. Within the approach suggested, they are written with the use of the characteristic differential equations for the variables Rd, z, and τdis. In particular, the equations for instantaneous diffraction Rd and “temporal” τdis rays are expressed in terms of the wave phase φ:

$$\frac{{d{{{\mathbf{R}}}_\text{d}}}}{{dz}} = \frac{{{{\nabla }_{ \bot }}\varphi ({{{\mathbf{R}}}_\text{d}},z;{{\tau }_{{{\text{dis}}}}})}}{{{{k}_{0}}}},\,\,\,\,\frac{{d{{\tau }_{{{\text{dis}}}}}}}{{dz}} = - k_{\omega }^{{{{''}}}}\frac{{\partial \varphi }}{{\partial t}}({{{\mathbf{R}}}_\text{d}},z;{{\tau }_{{{\text{dis}}}}}),$$
((1))

where \(k_{\omega }^{{{{''}}}} = {{\left. {\frac{{{{\partial }^{2}}k}}{{\partial {{\omega }^{2}}}}} \right|}_{{{{\omega }_{0}}}}}\) is the GDV coefficient; \(k = {{{{n}_{0}}\omega } \mathord{\left/ {\vphantom {{{{n}_{0}}\omega } c}} \right. \kern-0em} c}\) is the wavenumber at frequency ω; \({{n}_{0}} = \sqrt {{{\varepsilon }_{0}}} \) is the refractive index of an undisturbed medium; ε0 is its permittivity; and с is the speed of light in vacuum. In our case, we consider the parabolic form of the dispersion equation which is valid for rarefied gases: \(k(\omega )\,\,\, = \,\,\,{{k}_{0}} + k_{\omega }^{{{'}}}(\omega - {{\omega }_{0}})\,\,\, + \,\,\,0.5k_{\omega }^{{{{''}}}}{{(\omega - {{\omega }_{0}})}^{2}},\) where \({1 \mathord{\left/ {\vphantom {1 {k_{\omega }^{{{'}}}}}} \right. \kern-0em} {k_{\omega }^{{{'}}}}} = {{{v}}_\text{g}}\) is the group velocity of a radiation pulse.

Each diffraction ray (DR) is a spatial trajectory, the tangent to which coincides with the direction of an Poynting vector normalized to the wave intensity. When considering the problem of self-focusing and single filamentation of laser pulse in the context of radial symmetry in accordance with the amplitude-phase approach, the rotation of a DR around the laser beam axis determines the boundaries of the corresponding diffraction-beam tube (DBT). As a result, the laser beam can be represented as a set of nested DBTs each characterized by a finite cross section and carrying a certain amount of radiation power. The power which flows through any cross section of a tube remains constant, provided that there are no energy sources and sinks in the medium. This makes it possible to judge the effect of physical processes that occur with radiation in the medium by variations in the DBT form during radiation propagation, since these tubes do not exchange energy and do not intersect in space.

EFFECT OF THE GROUP VELOCITY DISPERSION ON THE LASER PULSE FILAMENTATION IN AIR

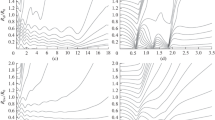
To estimate the dispersion effect on the parameters of the filamentation domain of Ti:Sapphire laser pulses, let us consider changes in the relative radii of DBTs with different initial relative peak power and beam radii shown in Fig. 1. The DBT radius is normalized to the initial beam radius R0, and the longitudinal coordinate z, to the Rayleigh length of the original beam. The trajectories of instantaneous DRs corresponding to the central time layer of a pulse τ = (t − z/vg)/tp = 0 are determined from the well-known wave phase profile φ during the solution of DR Eqs. (1).

Fig. 1.
figure 1

Relative DBT radii along the path for beams with the radius (a–c) R0 = 1 and (d–f) 3 mm, pulse length tр = 20 fs and relative peak power (a and d) η = 3, (b and e) 6, and (c and f) 9.

Full size image

For clarity, rays which correspond to energy-replenishing DBTs, i.e., tubes where the energy exceeds the energy loss during plasma formation throughout the filament lifetime, are bolded in Fig. 1. After the cease of filamentation, these tubes are transformed into high-intensity postfilamentation light channels (PFC). As noted in [14], these DBTs correspond to the energy reservoir in [15]. Parameters of energy-replenishing DBT are determined by initial laser radiation parameters and directly affect the general process pattern.

The comparison between the energy-replenishing DBT radii for pulses 20 (Fig. 1) and 100 fs in length (Fig. 5 in [13]) shows that the tube radius increases in the case of GVD manifestation. In addition, the dependence of the tube radius on the initial laser beam radius is traced for millimeter beams. In the absence of dispersion \((k_{\omega }^{{{{''}}}} = 0)\), the above dependence does not manifest itself for this class of beams. In this case, for pulses of small relative power (Fig. 1a), the radius of an energy-replenishing DBT may exceed the initial laser beam radius; in the absence of dispersion (see [13]), this is characteristic only of submillimeter laser beams. An increase in the energy-replenishing DBT radius when accounting for the dispersion is caused by pulse power leveling in its different time layers, i.e., a decrease in the power in the central time layer and its increase in the front layer as compared to the case of zero dispersion.

The differences in the structure of DRs constructed for beams with the same peak power but different initial radii are also seen. When GVD is taken into account, the absence of self-focusing and filamentation of an initially supercritical pulse (η > 1) can be connected not only with a small pulse peak power (Figs. 1a and 1d), but also with an increase in the initial beam radius (Fig. 1e). As a result, no plasma channels, where the density of free electrons is characteristic of the filamentation domain, are formed for laser pulses with certain parameters (Figs. 1a and 1d–1e).

The comparison of the diffraction-beam patterns for 20- (Fig. 1) and 100-fs pulses (Fig. 5 in [13]) made it possible to analyze the effect of GVD on the coordinate of the nonlinear beam focus normalized to the Rayleigh length. This coordinate determines the beginning of the filamentation domain, which is characterized by a certain (specified) free electron density of laser plasma ρе > 1020 m−3. As shown below, this situation may not occur due to the medium dispersion effect.

Figure 2 shows the dependence of the normalized coordinate of the nonlinear focus zf/LR on the initial laser beam radius for the central time layer (τ = 0) of pulses of various length.

Fig. 2.
figure 2

Normalized coordinate of nonlinear focus zf/LR as a function of the initial radius of a beam with η = 6.

Full size image

An increase in the initial beam radius results in a decrease in the normalized coordinate of the nonlinear focus with respect to the pulse source and in stabilization of the normalized coordinate for millimeter laser beams at a fixed initial peak power of 100-fs pulses.

If the GVD effect is enhanced, the normalized coordinate of the nonlinear focus is removed for 20-fs pulses at the same beam radii (region I in Fig. 2). Moreover, for millimeter laser beams, the character of the dependence of zf/LR on R0 changes, i.e., the normalized coordinate of the nonlinear focus increases with the initial beam radius (region II in Fig. 2), which indicates the enhancement of the dispersion effects for beams with larger initial radii. Thus, for a beam with the radius R0 = 3 mm, the normalized coordinate of the filamentation start shifts along the radiation propagation path more than two times farther for 20-fs pulses as compared to 100-fs pulses. The estimates of the characteristic scales of self-focusing and filamentation of laser pulses with parameters corresponding to Fig. 2 show that the dispersion effect for 20-fs pulses manifests itself even in the cases where the dispersion length is not a minimal scale among all the characteristic longitudinal scales of the problem.

Figure 3 illustrates the fact that the length of the radiation filamentation domain is reduced under the GVD effect. The angular divergence of the DBT also changes during the postfilamentation propagation. Moreover, if the pulse dispersion is taken into account, then the tubes are deformed more strongly and enter and exit the nonlinear focus at larger angles with respect to the propagation axis. As a result, if GVD is considered, then the angular divergence of the most intensive part of the beam PFC increases (two times on average in comparison with the dispersion free case [14]). The absolute values of the divergence are tenths of a milliradian.

Fig. 3.
figure 3

The relative DBT radii along the path for pulses with η = 6, R0 = 1 mm, tр = 20 fs with (solid curves) and without dispersion (dashed curves).

Full size image

We should especially note that the above increase in the normalized coordinate of the filamentation start is observed only for some time layers near the central layer and in the integral pattern constructed for pulse-averaged DRs if the medium dispersion is taken into account. Figures 4a and 4c show how the normalized coordinate of the nonlinear focus changes in different time layers of a laser pulse for beams with different initial radii for medium models with and without GVD. In this example, η = 6 (Figs. 4a and 4b) and 9 (Figs. 4c and 4d); tр = 20 fs.

Fig. 4.
figure 4

The normalized coordinate of nonlinear focus as a function of the initial radius for (a and c) different time layers of a laser pulse and maximal concentration of free electrons (b and d) during filamentation calculated taking with account of GVD (solid curves) and neglecting it (dashed curves).

Full size image

Note that not all nonlinear foci correspond to the beginning of the filamentation domain even for a central time layer if the dispersion is taken into account in the computational model. As can be seen from Figs. 4b and 4d, allowance for the dispersion results in a sharp decrease in the plasma density in the beam channel as the initial beam radius increases, which indicates low radiation intensity in the region of the nonlinear focus, insufficient for the high-intensity plasma channeling.

Figure 4a shows that the dispersion effect on the self-focusing can be ambiguous under variation in the initial beam radius. A change in the DBT power due to dispersion immediately affects the coordinate of the nonlinear focus. Since the front and rear pulse time layers are characterized by lower power as compared to the center layer, the nonlinear focus in these time layers is shifted along the propagation path from the laser source, which is observed in the absence of dispersion (dashed curves in Fig. 4a). In this case, self-focusing of the trailing edge of a pulse occurs earlier than of the leading edge due to the effect of nonlinear refraction in the plasma formed by the central layers.

When GVD is taken into account, the power in different time layers of a pulse is leveled due to the power flow from the previous time layers to the current one [11]; hence, the normalized coordinate of filamentation start changes more smoothly. A beam with R0 = 3 mm is focused at one point for all pulse time layers, since the self-focusing is suppressed by the dispersion in this case, and filamentation does not occur. In addition, the normalized coordinate of the nonlinear focus can be smaller in individual peripheral time layers if the dispersion is taken into account (R0 = 1 mm).

To explain the role of dispersion, we consider the power evolution in DBT. As is known, the radiation propagates through a dispersion medium under conditions of phase modulation, and additionally through a nonlinear medium with self-phase-modulation; therefore, high radiation intensity enhances the role of dispersion in a nonlinear medium. GVD leads to wave phase modulation in the medium, which affects the pulse intensity, power, and length and the filament structure and size. According to [11], one can write an equation which describes the DBT power evolution Pd. The DBT power conservation law within the diffraction-beam approach has the form

$$\frac{{\partial {{P}_\text{d}}}}{{\partial z}} = \left[ {\int\limits_0^{{{R}_\text{d}}(z,t)} {\frac{\partial }{{\partial t}}{{S}_\text{t}}d{{{\mathbf{r}}}_{ \bot }}} } \right] - {{\left\langle {{{\alpha }_\text{n}}} \right\rangle }_{\sigma }}{{P}_\text{d}},$$
((2))

where \({{S}_\text{t}} = k_{\omega }^{{{{''}}}}I{\kern 1pt} \frac{{\partial \varphi }}{{\partial t}}\) is the source function which characterizes a path variation in the energy flux density stored due to the dispersion in previous pulse time layers; \({{\left\langle {{{\alpha }_\text{n}}} \right\rangle }_{\sigma }}\) is the absorption coefficient averaged over the absorption cross section σ.

The first term in the right-hand side of Eq. (2) describes a change in the power due to phase modulation, and the second term, nonlinear losses. In other words, Eq. (2) shows that the power variation inside a DBT does not relate to the energy exchange between neighbor tubes but is caused only by losses due to plasma formation and energy redistribution within a pulse.

Fig. 5.
figure 5

The relative DBT power Pt/Pcr along the path z/LR for different time layers of a 20-fs pulse (a) with and (b) without dispersion; R0 = 1 mm, η = 6.

Full size image

The second time derivative of the wave phase determines the pulse chirp due to the GVD and Kerr and plasma nonlinearity. The chirp magnitude depends on the radiation intensity and changes in different time layers of a laser pulse. As a result, inevitable power loss in DBT can be compensated by power inflow from the preceding time layers. Then, the instantaneous balance of forces of focusing and defocusing nonlinearities can be restored (or set) in the tube, which maintains the filamentation.

Figure 5 shows variations in the relative DBT power Pt/Pcr along the path z/LR for time layers 1 < τ < 1 of a 20-fs laser pulse for the cases with GVD and without it. A DBT with the power equal to self-focusing critical power at the time point τ = 0 is taken.

One can see that the path variations in the DBT relative power significantly depend on the dispersive properties of the medium. Thus, the power in the tube is near constant or decreases in the regions of active plasma formation (−0.5 < τ < 0.5) in the absence of dispersion (Fig. 5b). The normalized focus coordinate should move along the path from the laser source in peripheral time layers where the power is lower than in the central layer, which is observed in the absence of dispersion (dashed curves in Figs. 4a and 4c). GVD provides an additional inflow of power from the preceding time layers of a pulse, and, as can be seen from Fig. 5a, the power in the tube increases at certain path points in the presence of dispersion at the pulse edges, which approaches the focus in the normalized coordinates (solid curves for R0 = 1 and 2 mm in Fig. 4). In this case, the dispersion (Fig. 5a) affects only the pulse edges, where the normalized focus coordinate increases as compared to the case without dispersion. The intensity decreases and the focus moves away in the central time layer in the presence of GVD due to the phase modulation.

ESTIMATION OF GVD EFFECT ON LASER PULSE FILAMENTATION BASED ON THE ANALYSIS OF CHARACTERISTIC SCALES

Let us consider an increase in the laser pulse intensity during its focusing in air. The integral representation of the intensity has been derived in [11]:

$$I({{{\mathbf{R}}}_\text{d}},z,t) = I\left( {{{{\mathbf{R}}}_\text{d}}(0),0,{{\tau }_{\text{dis}}}(0)} \right)\exp \left\{ {D(z)} \right\},$$
((3))

where

$$\begin{gathered} D(z) = \int\limits_0^z {\left[ { - \frac{{\nabla _{ \bot }^{2}\varphi }}{{{{k}_{0}}}}\left( {{{{\mathbf{R}}}_\text{d}}(z{\kern 1pt} '),z{\kern 1pt} ',{{\tau }_{{{\text{dis}}}}}(z{\kern 1pt} ')} \right)} \right.} \\ + \,\,k_{\omega }^{{{{''}}}}\frac{{{{\partial }^{2}}\varphi \left( {{{{\mathbf{R}}}_\text{d}}(z{\kern 1pt} '),z{\kern 1pt} ',{{\tau }_{{{\text{dis}}}}}(z{\kern 1pt} ')} \right)}}{{\partial {{t}^{2}}}} \\ \left. {^{{^{{^{{^{{^{{}}}}}}}}}} - \,\,{{\alpha }_\text{n}}\left( {{{{\mathbf{R}}}_\text{d}}(z{\kern 1pt} '),z{\kern 1pt} ',{{\tau }_{{{\text{dis}}}}}(z{\kern 1pt} ')} \right)} \right]dz{\kern 1pt} ', \\ \end{gathered} $$

\(\nabla _{ \bot }^{2}\) is the transverse Lapalacian; αn is the coefficient of nonlinear absorption due to plasma formation. Equation (3) is written in terms of spatial and “temporal” rays (1). Near the beginning of the propagation path, we can write

$$I(z) \approx I(0) + \frac{1}{2}\frac{{{{d}^{2}}I(0)}}{{d{{z}^{2}}}}{{z}^{2}}$$

for the case of the only Kerr nonlinearity effect εn = 2n0n2I (εn is the nonlinear addition to the medium permittivity, n2 is the nonlinearity factor) at αn = 0. Using Eq. (3), we derive

$$\frac{{{{d}^{2}}I(0)}}{{d{{z}^{2}}}} = \beta I(0),$$

where \(\beta = \frac{{d\gamma }}{{dz}}\), \(\gamma = {{\gamma }_\text{t}} - {{\gamma }_\text{r}};\)\({{\gamma }_\text{t}} = \frac{{{{\partial }^{2}}\varphi }}{{\partial {{t}^{2}}}}\) is the pulse chirp; \({{\gamma }_\text{r}} = \frac{{\nabla _{ \bot }^{2}\varphi }}{{{{k}_{0}}}}\) is the coefficient of spatial modulation of the wave phase. The wave phase is determined by the integral equation [11]

$$\varphi \left( {{{{\mathbf{R}}}_\text{d}}(z),z,{{\tau }_{{{\text{dis}}}}}(z)} \right) = \frac{{k{}_{0}}}{2}\int\limits_0^z {{{{\tilde {\varepsilon }}}_{\text{ef}}}\left( {{{{\mathbf{R}}}_\text{d}}(z{\kern 1pt} '),z{\kern 1pt} ',{{\tau }_{{{\text{dis}}}}}(z{\kern 1pt} ')} \right)dz} .$$

Here \({{\tilde {\varepsilon }}_{\text{ef}}} = {{{{\varepsilon }_{\text{ef}}}} \mathord{\left/ {\vphantom {{{{\varepsilon }_{{ef}}}} {{{\varepsilon }_{0}} - 1}}} \right. \kern-0em} {{{\varepsilon }_{0}} - 1}}\) is the disturbance of the effective permittivity of the medium; εef = ε0 + εn + εd + εdis; \({{\varepsilon }_\text{d}} = \frac{{{{\varepsilon }_{0}}\nabla _{ \bot }^{2}A}}{{k_{0}^{2}A}}\) is the diffraction and \({{\varepsilon }_{{{\text{dis}}}}} = - \frac{{{{\varepsilon }_{0}}k_{\omega }^{{{{''}}}}}}{{{{k}_{0}}A}}\frac{{{{\partial }^{2}}A}}{{\partial {{t}^{2}}}}\) is the dispersion component of the effective permittivity of the medium.

Let us consider the case of the weak diffraction effect on self-focusing, where the estimate

$${{\beta }_{t}} = - \frac{1}{{L_{{{\text{dis}}}}^{2}}}\left( {1 + \frac{{2L_{{{\text{dis}}}}^{{}}}}{{{{L}_{\text{n1}}}}}} \right),$$

is valid at τ = 0, where \({{L}_{{{\text{dis}}}}} = {{t_\text{p}^{2}} \mathord{\left/ {\vphantom {{t_{p}^{2}} {k_{\omega }^{{{{''}}}}}}} \right. \kern-0em} {k_{\omega }^{{{{''}}}}}}\) is the characteristic longitudinal scale of the problem for the condition of normal linear dispersion; \({{L}_{\text{n1}}} = {{{{n}_{0}}} \mathord{\left/ {\vphantom {{{{n}_{0}}} {({{k}_{0}}{{n}_{2}}{{I}_{0}})}}} \right. \kern-0em} {({{k}_{0}}{{n}_{2}}{{I}_{0}})}}\) is the length which characterizes the nonlinear phase incursion in the medium in the geometrical optics approximation, and I0 is the peak intensity of incident radiation connected with its peak power Р0 by the relation \({{P}_{0}} = \pi R_{0}^{2}{{I}_{0}}.\)

Let us estimate the coefficient of spatial modulation \({{\beta }_\text{r}} = - \frac{d}{{dr}}{{\gamma }_\text{r}}\) due to the Kerr nonlinearity and diffraction. The coefficient βr, connected with the nonlinear phase \({{\varphi }_\text{n}} = \frac{{{{k}_{0}}}}{2}\int_0^z {{{\varepsilon }_\text{n}}dz} \) is calculated in the aberration-free geometrical optics approximation and the specified intensity approximation at z = 0. Then, at τ = 0, like for the pulse chirp,

$$\beta _\text{r}^{n} = \frac{{4{{n}_{2}}{{I}_{0}}}}{{{{n}_{0}}R_{0}^{2}}} = \frac{2}{{L_{\text{n2}}^{2}}},$$

where \({{L}_{\text{n2}}} = \sqrt {\frac{{{{n}_{0}}}}{{2{{n}_{2}}{{I}_{0}}}}} {{R}_{0}}\) is the nonlinearity length calculated in the aberration-free approximation. In the physical sense, Ln2 determines the distance where the current beam radius changes by \(\sqrt 2 \) times as compared to its value at the entrance in a nonlinear medium.

Calculating the coefficient of phase modulation due to diffraction

$$\beta _\text{r}^\text{d} = - \frac{2}{{L_\text{d}^{2}}},$$

where \({{L}_\text{d}} = {{k}_{0}}R_{0}^{2}\) is the diffraction length, we derive

$$\beta = \frac{2}{{L_{\text{n2}}^{2}}} - \frac{1}{{L_{{{\text{dis}}}}^{2}}}\left( {1 + \frac{{2{{L}_{{{\text{dis}}}}}}}{{L_{\text{n1}}^{{}}}}} \right) - \frac{2}{{L_\text{d}^{2}}}.$$

Thus, we can introduce a scale for a dispersion medium with Kerr nonlinearity, which characterizes the effect of normal dispersion under conditions of nonlinearity:

$$L_{{{\text{dis}}}}^{\text{ef}} = {{L}_{{{\text{dis}}}}}{{\left( {1 + \frac{{2{{L}_{{{\text{dis}}}}}}}{{{{L}_{{{\text{n1}}}}}}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}.$$

The characteristic lengths for the problem are given in Table 1. The comparison between the diffraction, dispersion, and nonlinear scales allows one to estimate the effect which predominates during the femtosecond laser pulse propagation (it corresponds to the minimal scale).

Table 1.   Characteristics scales of self-focusing and filamentation of laser pulses
Full size table

Ln2 < Ld < Ldis for 100-fs pulses; therefore, the nonlinearity makes the greatest contribution to the self-focusing and filamentation of laser pulses. If the pulse length is reduced to 20 fs and the dispersion length is correspondingly decreased, then this relationship is true for submillimeter beams, while Ld > Ldis for millimeter beams with R0 > 1.56 mm. Despite the dispersion length not being the smallest scale for some initial laser pulse parameters, it affects the self-focusing and filamentation (see Fig. 4). This suggests that the conditions for the phase modulation of pulses under self-focusing change in comparison with a linear medium.

Table 1 shows that the effective dispersion length \(L_{{{\text{dis}}}}^{{{\text{ef}}}}\) is lower than \(L_{{{\text{dis}}}}^{{}}\) by several times for millimeter-radius beams and by orders of magnitude for submillimeter laser beams for 20-fs pulses. Thus, we can estimate a priori the effect of normal dispersion on self-focusing and filamentation of ultrashort laser pulses in air. For this effect, the condition \(L_{{{\text{dis}}}}^{{{\text{ef}}}}\) < Ln2 < Ld should be satisfied.

CONCLUSIONS

The study of the propagation of high-power femtosecond pulses of a Ti:sapphire laser in air based on the diffraction-beam tube approach shows the following. The radius of the energy-replenishing diffraction-beam tube with energy sufficient to compensate the beam energy loss throughout the lifetime of a filament increases, as well as the angular divergence of a postfilament channel, as the pulse length decreases from 100 to 20 fs. The coordinate of the filamentation start normalized to the Rayleigh length increases with the initial beam radius for millimeter laser beams under the effect of normal dispersion. It is possible to estimate the effect of normal dispersion on self-focusing and filamentation of femtosecond laser pulses in air using the expression for the modified dispersion length derived in this work.