INTRODUCTION

Evaporation is one of the most important in hydrological cycle and plays a significant role in water resources management. It is needed as input for modeling hydrological processes as well, soil, water, plant and atmosphere relations. Soil evaporation starts when soil moisture increase due to rainfall, irrigation or the capillary rise of water table. The amount of evaporated water depends on soil characteristics and climatic conditions of the atmosphere. In arid and semi-arid regions, a significant portion of water from rainfall that reaches the soil surface get lost due to evaporation. Even in the covered soils with vegetation, depends on type of irrigation method and plant growth stage, about 10 to 61% of evapotranspiration (ET) belongs to soil evaporation alone [36]. Therefore, soil evaporation is a major component of the hydrologic cycle particularly in arid areas under rainfed agriculture and pastures.

Generally, the capillary rise of groundwater from deeper levels causes salinization, resulting in concentration of salt at the soil surface. Therefore, a major difficulty associated with agriculture in areas overlying shallow ground water that is high in salt content is that saline water will move upward to the surface and evaporate, leaving behind salt deposits that can damage crops or deteriorate soil structures. Therefore, for salinity controlling caused by capillary rise from free water surface, the critical water table depth is predicted for drainage purposes [12]. The minimum depth of water table in the soil profile depends on texture and structure of soils and usually is considered to be 175 cm or more, so capillary rise and evaporation rate reduce to lower than 1 mm/day [23]. Consequently, evaporation is not only responsible for huge water loss through soil surface, but may also cause large scales soil salinization particularly in arid and semi-arid regions [28]. Effective methods for controlling evaporation from the soil surface only depend on awareness of the evaporation process in the different states and forms. For providing appropriate water table depth, relationship between the water table depth, soil characteristics and evaporation rate must be recognized [37].

Both experimental data and theoretical schemes have shown that three distinct evaporative stages of soil drying do exist [37]. In the first stage which is called “constant rate stage,” evaporation is governed by external atmospheric conditions. In this stage, evaporation is sustained as the soil water content decreases with time in the topsoil due to the hydraulic gradient increasing sufficiently to compensate for the decreasing hydraulic conductivity [35]. The second stage, falling rate stage, of evaporation is characterized by a gradual decrease of evaporation rate with time. In this stage, evaporation depends both on atmospheric conditions and the rate of transport of water from deeper parts of the profile to the soil surface. Because the increase of hydraulic gradient cannot compensate the decreasing hydraulic conductivity, the water movement to the soil surface decreases. The third stage, slow rate stage, begins after the surface zone becomes too dry so that further conduction of liquid water through it effectively stops. At this stage, low rate evaporation through dry layer of the soil occurs due to diffusion of vapor [12].

Several investigations have been conducted for determining the share of shallow water table depth for providing different crops water requirement. The results show that the water table at depths of 50–110 cm from the soil surface, provide about 41–75% of crops water requirement [8, 15, 16, 18, 19, 30, 34]. However, subsurface drain spacing is underestimated by the equations that do not account for evaporation (E) or evapotranspiration (ET) lowering the water table in drained lands. Several researchers showed that taking E/ET into account in the design of subsurface drain spacing leads to wider drain spacing by 9 to 24% [e.g. 1, 20, 23].

The main difficulty in accurate estimation of steady evaporation under field conditions is the lack of simple relations with minimum input requirements in terms of water losses in the water balance models. However, direct measurement of evaporation in large scales is difficult, costly, time consuming and usually impractical [37]. In this regard, many studies have been conducted and several measurement methods have been developed. Almost all of these methods are dependent on soils hydraulic parameters and water content in the soil profile. Theoretical studies on soil evaporation can be categorized into two steady and unsteady state conditions. Many researchers investigated steady-state upward flow [e.g., 4–6, 10, 13, 26, 32, 33]. Steady state solutions are based on Darcy-Buckingham law for upward flow in the saturated zone above constant and shallow water table. Unsteady evaporation studies can be divided into numerical and analytical solutions of Richards’ equation for upward flow in the unsaturated zone with initial and boundary conditions governing evaporation process. The use of numerical simulation models in the analysis of evaporation process under various initial and boundary conditions have been developed by several investigators [e.g., 2, 3, 9, 11, 25, 27]. These models make it possible to analyze the role of the time variable soil conditions at the surface as well as in depth. However, numerical solutions are complex and have difficulties in using rather than analytical solutions. Several researchers have derived analytical solution of the unsteady upward flow modelsfor semi-infinite and finite soil for an initially uniform wetted soil column in the presence or absence of groundwater table. These studies mainly focused on the one dimensional diffusion equation, neglecting thermal and gravity effects [e.g., 17, 22, 23, 29, 31, 36, 37].

This study aimed to improve the analytical and classical solution which presented by Gardner [5] for estimating steady evaporation rate from bare soils in the presence of shallow water table.

MATERIALS AND METHODS

Theoretical Scheme

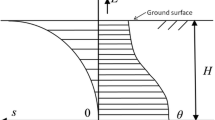
Although water evaporation in the field is not a steady-state process, a nearly steady upward flow from a shallow water table to bare soil surface may be established if the daily evaporative demand is reasonably uniform for a long period of time [14]. A Classic and analytical solution to this phenomenon presented by Gardner [5] and examined by Gardner and Fireman [6]. In such condition, which is presented in Fig. 1, it has been assumed that the maximum possible water evaporation rate occurs above a water table located at a distance Z = –L below the soil surface (Z = 0). The relationship between hydraulic conductivity and soil water pressure head can be expressed by the following functional form:

$$K(h) = \frac{{{{K}_{s}}}}{{1 + {{{\left( {\frac{h}{a}} \right)}}^{N}}}},$$
((1))
Fig. 1.
figure 1

Schematic representation of boundary conditions governing steady-state evaporation from shallow water table.

Full size image

where K(h) is the soil unsaturated hydraulic conductivity (LT–1), Ks is the saturated hydraulic conductivity (LT–1), h is the soil water pressure head (L) and N > 0 and a(L) < 0 are two constant parameters depending on soils type and the shape of K–h, curve.

In such situation, h1 = 0 at z1 = –L (the water table) and h2 → –∞ at z2 = 0 (the soil surface) representing the maximum capillary attraction to the soil surface and therefore the maximum evaporation rate. By changing the differential form of the Darcy-Buckingham flow equation to integral form, we may rewrite as [14]:

$${{J}_{w}} = - K(h)\left( {\frac{{dh}}{{dz}} + 1} \right),$$

or

$$\int\limits_{{{h}_{1}}}^{{{h}_{2}}} {\frac{{dh}}{{1 + \frac{{{{J}_{w}}}}{{K(h)}}}}} = - \int\limits_{{{h}_{1}}}^{{{h}_{2}}} {dz = {{z}_{1}} - {{z}_{2}}} ,$$
((2))

where Jw is flow rate (LT–1), dh is soil water pressure head (L) difference and dz is distance between any two points (L).

Letting Jw = +E represents the soil surface evaporation rate and using Eqs. (1) and (2), we can rewrite:

$$ - L = \int\limits_0^{ - \infty } {\frac{{dh}}{{1 + \left( {\frac{E}{{{{K}_{s}}}}} \right)\left( {1 + {{{\left( {\frac{h}{a}} \right)}}^{N}}} \right)}}} .$$
((3))

Letting the change of variables y = h/a > 0 in Eq. (3), the following change in the integral is produced:

$$ - L = a\int\limits_0^\infty {\frac{{dy}}{{1 + \left( {\frac{E}{{{{K}_{s}}}}} \right) + \left( {\frac{E}{{{{K}_{s}}}}} \right){{y}^{N}}}}} .$$
((4))

By assuming that E/Ks ⪡ 1, we have:

$$ - L \approx a\int\limits_0^\infty {\frac{{dy}}{{1 + \left( {\frac{E}{{{{K}_{s}}}}} \right){{y}^{N}}}}} .$$
((5))

Letting z = y (E/Ks)1/N in Eq. (5), the following change can be applied in the integral:

$$ - L = a{{\left( {\frac{{{{K}_{s}}}}{E}} \right)}^{{1{\kern 1pt} /N}}}\int\limits_0^\infty {\frac{{dz}}{{1 + {{z}^{N}}}}} .$$
((6))

The integral in Eq. (6) can be found in any standard table of definite integral or it can be evaluated by the calculus of residues [24]:

$$\int\limits_0^\infty {\frac{{dz}}{{1 + {{z}^{N}}}}} = \frac{\pi }{{N\sin \rightleftarrows \left( {\frac{\pi }{N}} \right)}}.$$
((7))

After substituting Eq. (7) in Eq. (6) and solving it, the maximum evaporation rate may be calculated by:

$$E = {{K}_{s}}{{\left( {\frac{{ - a\pi }}{{LN\sin \rightleftarrows \left( {\frac{\pi }{N}} \right)}}} \right)}^{N}}.$$
((8))

Equation (8) gives the maximum evaporation rate from bear soil (E) as function of the distance from the water table to the soil surface (L) and the soil hydraulic parameters (Ks, a, and N).

To calculate the integral in Eq. (4), it was assumed that E/Ks ratio is negligible (E/Ks ⪡ 1). Although this assumption is nearly true for coarse-textured soils, bout for heavy soils textures this ratio is considerable. For instance, if the daily evaporation rate in a region is 5 mm/day and the saturated hydraulic conductivity of two sandy loam and clay soil texture are 120 and 20 mm/day, the E/Ks ratio would be about 0.042 and 0.250, respectively.

In this study, we did not consider E/Ks ratio to be negligible and the integral in Eq. (4) was solved instead of the integral in Eq. (5). Letting b = E/Ks, and since b > 0, so b/(1 + b) > 0 and we will have:

$$\begin{gathered} \frac{{ - L}}{a} = \int\limits_0^\infty {\frac{{dy}}{{1 + b + b{{y}^{N}}}}} \\ = \frac{1}{{1 + b}}\int\limits_0^\infty {\frac{{dy}}{{1 + \left( {\frac{b}{{1 + b}}} \right){{y}^{N}}}}} \\ = \frac{1}{{1 + b}}\int\limits_0^\infty {\frac{{dy}}{{1 + {{{\left( {\left( {\sqrt[N]{{\frac{b}{{1 + b}}}}} \right)y} \right)}}^{N}}}}} . \\ \end{gathered} $$
((9))

If the change of variable \(x = \left( {\sqrt[N]{{\frac{b}{{1 + b}}}}} \right)\,y\) is applied to Eq. (9), we would lead to:

$$\begin{gathered} \left( {\sqrt[N]{{\frac{b}{{1 + b}}}}} \right)y = x \Rightarrow y \\ = x\left( {\sqrt[N]{{\frac{{1 + b}}{b}}}} \right) \Rightarrow dy = \left( {\sqrt[N]{{\frac{{1 + b}}{b}}}} \right)dx, \\ y \to \infty \Rightarrow x \to \infty , \\ y \to 0 \Rightarrow x \to 0, \\ \end{gathered} $$
$$\begin{gathered} \frac{{ - L}}{a} = \frac{1}{{1 + b}}\int\limits_0^\infty {\frac{{\left( {\sqrt[N]{{\frac{b}{{1 + b}}}}} \right)dx}}{{1 + {{x}^{N}}}}} \\ = \left( {\frac{1}{{1 + b}}} \right)\left( {\sqrt[N]{{\frac{b}{{1 + b}}}}} \right)\int\limits_0^\infty {\frac{{dx}}{{1 + {{x}^{N}}}}} . \\ \end{gathered} $$
((10))

The right integral in Eq. (10) is a definite integral that may be looked up in any standard mathematical text or it can be evaluated by the calculus of residues [24]. It has the following value:

$$\mathop \smallint \limits_0^\infty \frac{{dx}}{{1 + {{x}^{N}}}} = \frac{\pi }{{N\sin \left( {\frac{\pi }{N}} \right)}}.$$
((11))

Substituting Eq. (11) into Eq. (10) and simplifying it, we have:

$$\frac{{\left( {\frac{E}{{{{K}_{s}}}}} \right)}}{{{{{\left( {1 + \left( {\frac{E}{{{{K}_{s}}}}} \right)} \right)}}^{{N - 1}}}}} = {{\left( {\frac{{ - a\pi }}{{LN\sin \left( {\frac{\pi }{N}} \right)}}} \right)}^{N}}.$$
((12))

Equation (12) implicitly gives the maximum soil surface evaporation rate (E) as function of the distance (L) between the water table and the soil surface, and the soil parameters Ks, a, and N are used to model the hydraulic conductivity function.

As it is presented here, for determining upward water transfer rate in liquid form, the soil hydraulic conductivity and soil water pressure head relation is assumed to conform to an empirical function which originally suggested by Gardner [5]. However, almost a similar derivation has previously been proposed by Ripple et al. [26]. They used a modified form of hydraulic conductivity and soil water pressure head function [7] which demonstrates more clearly the physical significance of the coefficients as following:

$$K = {{K}_{{\left( S \right)}}} = \frac{{{{K}_{{{\text{Sat}}}}}}}{{{{{\left( {\frac{S}{{{{S}_{{\frac{1}{2}}}}}}} \right)}}^{n}} + 1}},$$
((13))
$$\left( {\frac{E}{{{{K}_{{{\text{Sat}}}}}}} + 1} \right){{\left( {\frac{{\frac{E}{{{{K}_{{{\text{Sat}}}}}}}}}{{\frac{E}{{{{K}_{{{\text{Sat}}}}}}} + 1}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 n}} \right. \kern-0em} n}}}}\left( {\frac{L}{{{{S}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right) = \frac{\pi }{{n\sin \left( {\frac{\pi }{n}} \right)}},$$
((14))

where K(S) is hydraulic conductivity for liquid flow (LT–1), KSat is hydraulic conductivity of water saturated soil (LT–1), S is the soil water pressure head, which defined as the negative of the soil water pressure head (L), S1/2 is a constant coefficient representing S at \(K = \frac{1}{2}{{K}_{{{\text{Sat}}}}}\) (L) and n (–) is integer soil coefficient which usually ranges from 2 for clays to 5 in sands, and E is the rate of evaporation from the soil surface (LT–1).

Comparison of the Original and Improved Models

To verify the performance of Eq. (12), the original Gardner and Fireman [6] laboratory experimental data were used. In that experiment, some plexi-glass cylinders with 12 cm diameter and 60–100 cm length have been packed uniformly with two air-dried soils. The soils had fine sandy loam and clay textures. A water table has been then maintained at the bottom of each soil column by means of a buret arranged as a Mariotte bottle. The rate of loss of water from the buret served as a measure of the evaporation rate once the steady state was attained. The soil columns have been placed upon a slowly rotating table with an oscillating fan arranged to blow across the tops of the columns and four heat lamps placed 45 cm directly above the path of the tops of the columns. The evaporative conditions have been varied by varying the rate of air circulations and the amount of incident radiant energy [6].

In order to study the relation between evaporation rate and depth to the water table, columns similar to those described above were packed with soil, with an array of porous cups in the bottom of each column. The columns were partially dried and rewetted two or three times since this treatment tended to stabilize the structure and give results more nearly in agreement with field data. The cups in each column were connected through a manifold and a long copper tube to buret arranged as a Mariotte bottle. The buret for each column could be lowered to any depth below the soil surface down to 750 cm, thus simulating a variable water table. Tensiometers were placed at two or three depths in some of the columns. The simulated water table was lowered in increments of about 60 cm and ample time was allowed for steady state to be attained at each depth before lowering the next depth. At steady state the rate of loss of water from the buret equals the evaporation rate. The tensiometer readings gave assurance the steady state had been attained.

Table 1 summarizes values of parameters of hydraulic conductivity and soil water pressure head function (Eq. (1)) that were fitted to two fine sandy loam and clay soils [14].

Table 1.   The parameter values of Ks, a, and N for the experimental soils [14]
Full size table

For quantitative comparison of measured and estimated values of evaporation rates in the presence of water table, as well as for evaluating model performance, analysis of residual errors, differences between measured and predicted values were used [21, 37]. These are maximum coefficient of determination (CD), root mean square error (RMSE), and modeling efficiency (EF). The mathematical expressions of these statistics can be written as:

$${\text{CD}} = \frac{{\sum\limits_{i = 1}^n {{{{({{O}_{i}} - \bar {O})}}^{2}}} }}{{\sum\limits_{i = 1}^n {{{{({{P}_{i}} - \bar {O})}}^{2}}} }},$$
((15))
$${\text{RMSE}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{{({{P}_{i}} - {{O}_{i}})}}^{2}}} }}{n}} ,$$
((16))
$${\text{EF}} = \frac{{\sum\limits_{i = 1}^n {{{{({{O}_{i}} - \bar {O})}}^{2}}} - \sum\limits_{i = 1}^n {{{{({{P}_{i}} - {{O}_{i}})}}^{2}}} }}{{\sum\limits_{i = 1}^n {{{{({{O}_{i}} - \bar {O})}}^{2}}} }},$$
((17))

where Oi is the observed values, Pi is the predicted values, \(\bar {O}\) is mean of the observations, and n is the number of samples.

The CD statistics gives the ratio between the scatter of simulated values and that of the measurements. The RMSE is a frequently used measure of the difference between values predicted by a model and the values actually observed from the environment that is being modelled. The EF value is commonly used to assess the predictive power of hydrological discharge models. However, it can also be used to quantitatively describe the accuracy of model outputs for other things than discharge (such as nutrient loadings, temperature, concentrations etc.). The lower limit for CD is zero. The large RMSE value shows how much the simulations overestimate or underestimate the measurements. EF can range from –∞ to 1. An efficiency of 1 (EF = 1) corresponds to a perfect match between model and observations. An efficiency of 0 indicates that the model predictions are as accurate as the mean of the observed data, whereas an efficiency less than zero (–∞ < EF < 0) occurs when the observed mean is a better predictor than the model [37]. If all simulated and measured data are the same, the statistics yield CD = 1; RMSE = 0; EF = 0.

RESULTS AND DISCUSSION

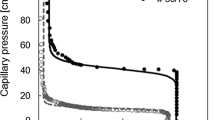
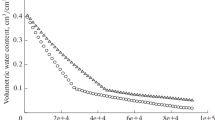
Using parameters values of hydraulic conductivity-soil water pressure head, the soil surface evaporation rate at different water table depths were obtained by two analytical models. The water table depths were varied between 0–750 cm for two soil textures. The estimated values by Eqs. (8) and (12) and those measured by Gardner and Fireman [6] were compared for two soil textures in Figs. 2 and 3, respectively. Both Figs. 2 and 3 show that not only the original model, but in some extent the improved model, underestimate the evaporation rate. This can be related to fact that both Eqs. (8) and (12) do not account for that part of evaporation which occurs as upward vapor phase. It can be followed from Figs. 4 and 5 that these two models can better predict evaporation rates when water table is relatively deeper. The reason can be attributed to the boundary conditions governing the evaporation process. To derive Eqs. (8) and (12), we assumed that at soil surface (z2 = 0), the pressure head is infinite (h2 → –∞) to theoretically solve the integral in Eq. (3). However, when the water table is near soil surface, the validity of this assumption is doubtful. Consequently, under very shallow water table conditions, determination of evaporation rate is practically impossible and its amount tends to infinity. In the clay soil texture, evaporation rate is larger than that of sandy loam soil under high water table conditions. Coarse-textured soils mostly contain large pores that drain out water at modest pressure heads and characterized in the model by larger values of N than the finer textured soils, which have a broader distribution of pore sizes. As a consequence, when the distance between water table and soil surface is large enough, the coarse-textured soils offer more resistance to upward water flow than finer textured soils. The upward water flow in fine-textured soils can be more significant than in coarse-textured soils. Thus, to avoid soil salinization, water table must be kept lower for fine-textured soils than for coarse-textured ones in drainage activities. For solving the integral in Eq. (4), it was assumed by Gardner that E/Ks ratio is negligible. Although this assumption is nearly true for coarse-textured soils, but for heavy soil textures this ratio is considerable. For this reason, our proposed analytical solution provided better estimation than the Gardner model particularly in fine-textured soil.

Fig. 2.
figure 2

Measured and estimated values of evaporation rate from the sandy loam soil surface by Eqs. (8) and (12) in different water table depths (observation data taken from [6]).

Full size image
Fig. 3.
figure 3

Comparison of the estimated evaporation rates from the clay soil with Eqs. (8) and (12) and those obtained by [6] in different water table depths.

Full size image
Fig. 4.
figure 4

Comparison of predicted evaporation rates from sandy loam soil obtained with Eqs. (8) and (12) and those presented by [6].

Full size image
Fig. 5.
figure 5

Comparison of evaporation rates from clay soil predicted with Eqs. (8) and (12) and those obtained by [6].

Full size image

The calculated values of CD, RMSE and EF statistics for the measured and predicted evaporation rates based on Eqs. (8) and (12) are given in Table 2. As can be seen in this Table, the obtained largest CD belongs to Eq. (12) that indicates a better prediction between simulated values and that of the measurements for both soil textures. However, the calculated RMSE for Eq. (12) is lower than that of Eq. (8). The large RMSE value for Eq. (8) shows how much the simulations more underestimate the measurements. As well, the modeling efficiency (EF) of Eq. (12) is better than Eq. (8) for the two experimental soil textures. The large EF value for Eq. (12) shows better match between model output and observations.

Table 2.   The calculated statistics for evaluating the model performances
Full size table

CONCLUSIONS

In the field condition, evaporation from bare soil surface is a dynamic phenomenon due to varying the hydraulic gradient in the topsoil with time. Therefore, both soil water content and hydraulic conductivity play important role in the rate of transport of water from deeper parts of the profile to the soil surface and then in evaporation rate. The assumption that E/Ks ratio is not negligible in the soils particularly for fine-textured soils and incorporating this ratio to solve the upward steady-state flow equation can improve the accuracy of estimating evaporation rate in the presence of shallow water table. In this research by incorporating E/Ks ratio in the upward flow derivation, the original model of Gardner is modified. Quantitative comparison of experimental data and those predicted with both models show that the prediction of evaporation rate in the presence of shallow water table is significantly improved by our proposed model.