Developing Approaches to Analysis of Melt Motion on the Surface of a Fuel Pin

Abstract

Based on the analysis of experiments carried out on simulators of fuel elements with a cladding of low-melting metals, models of melting and movement of the melt over the surface of fuel elements are proposed. The presented work is a continuation of experimental and theoretical work carried out jointly at the Nuclear Safety Institute, Russian Academy of Sciences, and Kutateladze Institute of Thermophysics, Siberian Branch, Russian Academy of Sciences, to study the features of the movement of a melt over a cylindrical surface that simulates the surface of a fuel element. It analyzes the factors that determine the thermal destruction of fuel elements. One of the important conclusions drawn from the analysis of experimental data was the conclusion about the prevailing film laminar runoff in the heated part of the fuel element simulator. Using this assumption, an analytical model was built that allows predicting the mass of a fuel element carried out of its limits during melting. As a result of calculations using the proposed model, it was shown that, for an accident with the introduction of positive reactivity, when the power increase can reach ten ratings, a modification of the model is necessary to take into account the turbulent runoff regime. For this purpose, a simplified model of the flow of the melt was built. A comparison is made with known techniques and it is shown that the proposed approach makes it possible to describe the turbulent flow regime with satisfactory accuracy. The modified model made it possible to calculate the features of the movement of a stainless steel melt over the surface of a fuel element of a fast neutron (BN) reactor. Information was obtained on the thickness of the melt, its velocity and Reynolds number, depending on the conditions of drainage, and on the mass carried outside the core.

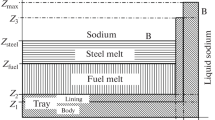
The first stage of a severe accident in a reactor facility is accompanied by the destruction of fuel elements in it. The reason for the destruction of fuel elements is a violation of the thermal balance in the core caused by a decrease in the cooling intensity of the fuel elements due to a decrease in the coolant flow rate with a constant energy release or a sharp increase in energy release due to the introduction of excessive positive reactivity. It is necessary to carry out a numerical calculation of such processes in order to analyze the consequences of severe accidents. Therefore, algorithms should be developed based on the modern understanding of the features of the destruction of fuel pins. The fuel pins of FB reactors have an active part, in which the main energy release occurs, and a blanket, in which there is virtually no energy release (Fig. 1). The presence of a cold blanket part can significantly affect the movement of the melt during its solidification. One of the obstacles to the development of algorithms is the lack of reliable experimental data. For this reason, experimental studies on the melting of fuel rod cladding simulators were carried out at the Institute for Safe Development of Nuclear Power Engineering, Russian Academy of Sciences, and Kutateladze Institute of Thermophysics, Siberian Branch, Russian Academy of Sciences, during which the melting and movement of the melt were studied and the temperature of the cladding and its mass loss were measured [1, 2].

Fig. 1.

Fuel pin diagram.

MODEL OF THE MASS LOSS OF THE SHELL DURING ITS MELTING

One of the important conclusions drawn from the analysis of experimental data is that the melt that flows down in the heated part of the fuel element simulator occurs in the film laminar mode [1, 2]. Taking into account this assumption and the results of work [3], the expression for calculating the mass average velocity of the melt flow U in the laminar regime of its flowing over a cylindrical surface and the simultaneous action of gravity and friction stress with a gas flow, it can be written in the following form:

$$\begin{gathered} U = \frac{{{{\rho }}g}}{{8{{\mu }}}}\left[ {{{{\left( {R + {{\delta }}} \right)}}^{2}} - {{R}^{2}}} \right] + \frac{{{{R}^{2}}}}{{{{{\left( {R + {{\delta }}} \right)}}^{2}} - {{R}^{2}}}} \\ \times \,\,\left[ {\left( {R + {{\delta }}} \right)\frac{{{{{{\tau }}}_{c}}}}{{{\mu }}} - \frac{{{{\rho }}g{{{\left( {R + {{\delta }}} \right)}}^{2}}}}{{2{{\mu }}}}} \right] \\ \times \,\,\left[ {{{{\left( {1 + \frac{{{\delta }}}{R}} \right)}}^{2}}\ln \left( {1 + \frac{{{\delta }}}{R}} \right) - \frac{1}{2}{{{\left( {1 + \frac{{{\delta }}}{R}} \right)}}^{2}} + \frac{1}{2}} \right], \\ \end{gathered} $$

(1)

where ${{\rho }}{\text{,}}$ ${{\mu }}{\text{,}}$ and ${{\delta }}$ are density, dynamic coefficient of viscosity, and thickness of the melt film, respectively; $R$ is radius of the surface over which the melt flows; g is gravitational acceleration; and ${{{{\tau }}}_{c}} = \frac{{{\xi }}}{8}{{{{\rho }}}_{c}}U_{c}^{2}$ is the friction stress between the melt and the gas flow (here ${{\xi }} = 0.02$ is coefficient of friction, index c is from English coolant).

Melt film weight m_f calculated by the equation

$${{m}_{f}} = {{\rho }}L{{\pi }}\left[ {{{{\left( {R + {{\delta }}} \right)}}^{2}} - {{R}^{2}}} \right],$$

where L is cladding length and $R = {{R}_{1}} - \Delta$ (here ${{R}_{1}}$ is initial outer radius of the shell; $\Delta$ is the thickness of the molten part of the fuel pins cladding, index f is from English film).

Total mass of the melt ${{m}_{l}}$ (index l from English liquid), formed as a result of melting of the fuel element cladding, is calculated by the expression

$${{m}_{l}} = {{\rho }}L{{\pi }}\left( {R_{1}^{2} - {{R}^{2}}} \right).$$

In the above expressions, the melting of the cladding from the inside is taken into account due to the heat exchange between it and the fuel core. In this case, the melt runoff, as was found in [1, 2], occurs along the outer surface of the cladding.

The equations of the conservation of the cladding melt mass and the thickness of its film, taking into account the fact that its formation is determined by melting, and its disappearance by dripping, are as follows:

$$\begin{gathered} \left\{ \begin{gathered} {{{\text{d}}{{m}_{f}}} \mathord{\left/ {\vphantom {{{\text{d}}{{m}_{f}}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = {N \mathord{\left/ {\vphantom {N {\Delta h - U{{\rho \pi }}\left[ {{{{\left( {{{R}_{1}} - \Delta + {{\delta }}} \right)}}^{2}} - {{{\left( {{{R}_{1}} - \Delta } \right)}}^{2}}} \right];}}} \right. \kern-0em} {\Delta h - U{{\rho \pi }}\left[ {{{{\left( {{{R}_{1}} - \Delta + {{\delta }}} \right)}}^{2}} - {{{\left( {{{R}_{1}} - \Delta } \right)}}^{2}}} \right];}} \hfill \\ {{{\text{d}}{{m}_{l}}} \mathord{\left/ {\vphantom {{{\text{d}}{{m}_{l}}} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = {N \mathord{\left/ {\vphantom {N {\Delta h;}}} \right. \kern-0em} {\Delta h;}} \hfill \\ \end{gathered} \right. \hfill \\ \left\{ \begin{gathered} {{{\text{d}\delta }} \mathord{\left/ {\vphantom {{{\text{d}\delta }} {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = {N \mathord{\left/ {\vphantom {N {\left( {2\Delta h{{\rho }}L{{\pi }}R} \right) - U{{\left[ {{{{\left( {R + {{\delta }}} \right)}}^{2}} - {{R}^{2}}} \right]} \mathord{\left/ {\vphantom {{\left[ {{{{\left( {R + {{\delta }}} \right)}}^{2}} - {{R}^{2}}} \right]} {\left[ {2L\left( {R + {{\delta }}} \right)} \right];}}} \right. \kern-0em} {\left[ {2L\left( {R + {{\delta }}} \right)} \right];}}}}} \right. \kern-0em} {\left( {2\Delta h{{\rho }}L{{\pi }}R} \right) - U{{\left[ {{{{\left( {R + {{\delta }}} \right)}}^{2}} - {{R}^{2}}} \right]} \mathord{\left/ {\vphantom {{\left[ {{{{\left( {R + {{\delta }}} \right)}}^{2}} - {{R}^{2}}} \right]} {\left[ {2L\left( {R + {{\delta }}} \right)} \right];}}} \right. \kern-0em} {\left[ {2L\left( {R + {{\delta }}} \right)} \right];}}}} \hfill \\ {{{\text{d}}\Delta } \mathord{\left/ {\vphantom {{{\text{d}}\Delta } {{\text{d}}t}}} \right. \kern-0em} {{\text{d}}t}} = {N \mathord{\left/ {\vphantom {N {\left( {2\Delta h{{\rho }}L{{\pi }}R} \right),}}} \right. \kern-0em} {\left( {2\Delta h{{\rho }}L{{\pi }}R} \right),}} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $$

where t is time, N is heater power, and $\Delta h$ is specific heat of fusion.

Using these equations, one can determine the mass loss at any time. It should be noted that these equations were obtained under the assumption that the velocity profile in the melt film over the melt thickness is established practically instantaneously, regardless of the melt formation rate. The validity of this approach will be substantiated further by comparing the calculation results and experimental data presented in the literature.

MODEL VALIDATION

To validate the model, we used the data of experimental studies by the authors of the mass loss rate Δm cladding simulators of fuel elements during their melting [1, 2]. The experiments were carried out using model cladding made of lead-bismuth alloy or tin. The calculation results and experimental data from [1, 2] are shown in Figs. 2 and 3.

Fig. 2.

Experimental (1) dependence and (2) calculated rate of weight loss of the eutectic Pb (44.5%)–Bi (55.5%) alloy on time, t. N, W: 3—93.0; 4—170.5; 5—259.7.

Fig. 3.

Experimental (1) dependence and (2) calculated rate of mass loss Sn versus time. N, W: 3—91.0; 4—174.4; 5—262.2.

The fuel pin simulator had a length of 0.18 m. A model cladding 0.001 m thick was deposited on it. Inside the simulator, there was a tubular cylindrical heater on which the model cladding was applied. The lower part of the cladding 0.02 m long was unheated and simulated the cold part of the fuel element. The length of the upper heated part of the model shell was 0.16 m.

As follows from the figures, the presented model makes it possible with satisfactory accuracy to simulate the mass loss of the model shell during its melting. Differences are observed only at the lowest energy release for the tin shell. The lower rate of mass loss of the melt can be explained by its partial freezing on the cold, lower part of the simulator (blanket) and a decrease in its drainage rate. In the above mathematical model, freezing on the surface is not taken into account.

Using the developed model, calculations were carried out for a shell made of stainless steel of type 316 (foreign classification, analogous to Kh18N12M3) at a nominal power release in the core of a 450 MW/m³ reactor plant type FB [4]. An accident was considered in which a sharp decrease in the coolant flow rate occurs due to pump shutdown at a constant reactor power (loss of coolant accident of the ULOF (Unprotected Loss of Flow) type), coolant boiling, a heat transfer crisis and, as a consequence, melting of the fuel element cladding. The length of the model fuel element was 1.0 m, the radius was 0.005 m, and the cladding thickness was 0.001 m.

Data transfer from the model melt to the melt related to the real cladding of a fuel element can be performed in accordance with the Reynolds number similarity theory

$$\operatorname{Re} = \frac{{4{{\rho }}U{{\delta }}}}{{{\mu }}} = - \frac{{{\text{d}}m}}{{{\text{d}}t}}\frac{2}{{{{\mu \pi }}R}} = \frac{{q{{\delta }}L}}{{{{\mu }}\Delta h}},$$

where q is heat flux from the surface of the fuel rod.

The moving gas in this case (see Fig. 1) is sodium vapor, which is formed due to its boiling. It should be noted that the steam velocity can reach several hundred meters per second due to the high energy loading of the core and the tightness of the rod bundle. Indeed, in accordance with the law of conservation of mass, the following estimate can be made:

$${{U}_{g}} = \frac{{4q{{L}_{r}}{{n}_{r}}}}{{{{D}_{h}}\Delta {{h}_{e}}{{{{\rho }}}_{{{\text{Na}}}}}}},$$

where U_g is the sodium vapor velocity, ${{L}_{r}}$ is fuel rod length, n_r is the number of rods in the fuel assembly (index r from English rod), D_h is hydraulic diameter of the fuel assembly (index h from English heat), $\Delta {{h}_{e}}$ is specific heat of vaporization (index e from English evaporation), and ${{{{\rho }}}_{{{\text{Na}}}}}$ is the sodium vapor density.

When $q = {{10}^{6}}$ W/m², ${{n}_{r}} = 300,$ ${{D}_{h}} = 3 \times {{10}^{{ - 3}}}$ m, $\Delta {{h}_{e}} = 4 \times {{10}^{6}}$ J/kg, ${{\rho }} = {{10}^{3}}$ kg/m³, $L = 1$ m, the speed of sodium vapor is 100 m/s.

Results of calculating the mass loss at different rates of blowing a fuel element with a gas flow U_g, (index g from English gas), the thickness of the melt film, and the Reynolds number are shown in Fig. 4. In Fig. 4a, “Heat balance” denotes the solution of a system of equations in which it is assumed that all the melt that was formed as a result of melting flows out instantly, i.e., without taking into account the final flow rate. In Fig. 4b two peaks are observed in the calculation of the Reynolds number at a gas velocity of 150 m/s. The first peak is associated with the carryover of the melt through the upper boundary of the fuel element, the second with the fact that, with a gradual increase in the film thickness due to melting, gravitational forces begin to exceed the friction force with the gas flow. As a result, the direction of movement of the melt is reversed, i.e., the melt begins to flow through the lower boundary.

Fig. 4.

Dependences of the (a) rate of weight loss of steel 316 in the laminar flow of the melt, (b) Reynolds numbers, and (c) the thickness of the melt film from time. U_g, m/s: 1—0; 2—50; 3—100;—150; 5—heat balance.

Moreover, it can be concluded from Fig. 4c that the thickness of the melt film does not exceed 0.8 mm, which indicates the possibility of considering the film for a fuel element 8 mm in diameter as relatively thin. In this case, the expression for the melt flow rate can be written in the form

$$U = \frac{{{{{{\tau }}}_{c}}{{\delta }}}}{{2{{\mu }}}} - \frac{{{{\rho }}g{{{{\delta }}}^{2}}}}{{3{{\mu }}}}.$$

(2)

The possibility of using this assumption was tested independently by comparing the results of calculations using formulas (1) and (2). It is known that formula (2) is valid at low gas velocities, at least before flooding. The possibility of transferring the formula to higher ranges will be presented below by comparing the calculation results for it with the available experimental data and known empirical formulas.

It also follows from Fig. 4b that, even for the nominal energy release, the Reynolds number for the melt is slightly higher than the critical value when passing from a laminar flow to a turbulent one (Re = 2000). Thus, for accidents with a loss of coolant flow rate ULOF, when the energy release is close to the nominal value, or accidents of the LOF type (loss of flow), when the reactor operates at the level of residual energy release, it can be assumed that a laminar regime of film runoff will be realized. For an accident with a power surge of the UTOP (unprotected transient over power) type, when the power can be several times higher than the nominal, the simplified laminar drainage model will be incorrect. For this reason, the development of simplified approaches to calculating the motion of the melt in laminar and turbulent regions is required.

IMPROVEMENT OF THE MODEL

The speed of the melt can be calculated based on the balance of the acting forces

$${{{{\tau }}}_{w}}{{\Pi }_{w}} = {{{{\tau }}}_{c}}{{\Pi }_{c}} - {{\rho }}gS,$$

where τ_w is friction stress on the wall in the laminar flow regime (index w from English wall), ${{\Pi }_{w}} = 2{{\pi }}R$ is wetted fuel element perimeter, ${{\Pi }_{c}} = 2{{\pi }}\left( {R + {{\delta }}} \right)$ is the perimeter of the contact between the melt and the coolant, and $S = {{\pi }}{{\left( {R + {{\delta }}} \right)}^{2}} - {{\pi }}{{R}^{2}}$ is the cross-sectional area of the melt.

In the presented expression, it is taken into account that the melt, due to friction, moves upward with the gas flow, while downward under the action of gravity. For a thin film, the expression for τ_w can be simplified:

$${{{{\tau }}}_{w}} = {{{{\tau }}}_{c}} - {{\rho }}g{{\delta }}{\text{.}}$$

Using the balance equation, the melt flow rate can be found by solving the nonlinear equation

$${{\xi }}\left( {\operatorname{Re} } \right){{U}^{2}} = \frac{{8\left| {{{{{\tau }}}_{c}} - {{\rho }}g{{\delta }}} \right|}}{{{\rho }}}.$$

The calculation of the friction stress in the laminar flow regime is carried out according to the formula [5]

$${{{{\tau }}}_{w}} = \frac{{2\left( {3{{\alpha }} - 1} \right){{\mu }}U}}{{{{\alpha \delta }}}},$$

where α is the coefficient taking into account the unevenness of the velocity profile over the thickness of the melt.

Here

$${{\alpha }} = {{\left( {3 + r} \right)} \mathord{\left/ {\vphantom {{\left( {3 + r} \right)} 6}} \right. \kern-0em} 6},$$

where $r = {{{{\rho }}g{{\delta }}} \mathord{\left/ {\vphantom {{{{\rho }}g{{\delta }}} {\left[ {2{{{{\tau }}}_{c}} + {{\rho }}g{{\delta }}} \right]}}} \right. \kern-0em} {\left[ {2{{{{\tau }}}_{c}} + {{\rho }}g{{\delta }}} \right]}}.$

If the melt profile is described by a power function with exponent n, then ${{\alpha }} = {1 \mathord{\left/ {\vphantom {1 {\left( {n + 1} \right)}}} \right. \kern-0em} {\left( {n + 1} \right)}}.$

For a turbulent flow, under the assumption of a power law of the velocity distribution (at n = 1/7) [5, 6], the following relation can be obtained:

$${{{{\tau }}}_{w}} = {{{{\xi }}}_{w}}{{{{\rho }}{{U}^{2}}} \mathord{\left/ {\vphantom {{{{\rho }}{{U}^{2}}} 8}} \right. \kern-0em} 8},$$

(3)

where ${{{{\xi }}}_{w}} = 0.37{{\left( {4U{{{{\delta \rho }}} \mathord{\left/ {\vphantom {{{{\delta \rho }}} {{\mu }}}} \right. \kern-0em} {{\mu }}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 4}} \right. \kern-0em} 4}}}}$ = ${{0.37} \mathord{\left/ {\vphantom {{0.37} {{{{\operatorname{Re} }}^{{0.25}}}}}} \right. \kern-0em} {{{{\operatorname{Re} }}^{{0.25}}}}}.$

Following the technique proposed in [6], for a turbulent flow, as a self-similar velocity profile, one can apply the power law of distribution over the melt thickness

$$u\left( y \right) = {{U}_{s}}{{\left( {{y \mathord{\left/ {\vphantom {y {{\delta }}}} \right. \kern-0em} {{\delta }}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}},$$

where ${{U}_{s}}$ is the velocity on the surface of the melt (index s from English surface).

According to [6], the expression for determining the thickness of the viscous sublayer δ_v (index v from English viscous) looks like this:

$${{{{\delta }}}_{{v}}} = {{{{\alpha }}}_{{v}}}{{{\mu }} \mathord{\left/ {\vphantom {{{\mu }} {\left( {{{\rho }}{{U}_{*}}} \right)}}} \right. \kern-0em} {\left( {{{\rho }}{{U}_{*}}} \right)}},$$

where ${{{{\alpha }}}_{{v}}}$ = 11.5 is model parameter and ${{U}_{*}} = \sqrt {{{{{{{\tau }}}_{w}}} \mathord{\left/ {\vphantom {{{{{{\tau }}}_{w}}} {{\rho }}}} \right. \kern-0em} {{\rho }}}}$ is pulsation speed.

Because ${{{{\tau }}}_{w}} = {{{{\xi }}}_{w}}{{{{\rho }}{{U}^{2}}} \mathord{\left/ {\vphantom {{{{\rho }}{{U}^{2}}} 8}} \right. \kern-0em} 8},$ you can write the following expression:

$${{{{U}_{*}}} \mathord{\left/ {\vphantom {{{{U}_{*}}} U}} \right. \kern-0em} U} = \sqrt {{{{{{{\xi }}}_{w}}} \mathord{\left/ {\vphantom {{{{{{\xi }}}_{w}}} 8}} \right. \kern-0em} 8}} .$$

In accordance with [6], the formula for the velocity of the melt at the boundary of the viscous sublayer can be written in the form

$${{u}_{{v}}} = {{{{\alpha }}}_{{v}}}{{U}_{*}}.$$

At the same time, when using a power-law velocity profile

$${{{{u}_{{v}}}} \mathord{\left/ {\vphantom {{{{u}_{{v}}}} {{{U}_{s}}}}} \right. \kern-0em} {{{U}_{s}}}} = {{\left( {{{{{{{\delta }}}_{{v}}}} \mathord{\left/ {\vphantom {{{{{{\delta }}}_{{v}}}} {{\delta }}}} \right. \kern-0em} {{\delta }}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}},$$

from which ${{{{{{\alpha }}}_{{v}}}{{U}_{*}}} \mathord{\left/ {\vphantom {{{{{{\alpha }}}_{{v}}}{{U}_{*}}} {{{U}_{s}}}}} \right. \kern-0em} {{{U}_{s}}}}$ = ${{\left( {{{{{{{\alpha }}}_{{v}}}{{\mu }}} \mathord{\left/ {\vphantom {{{{{{\alpha }}}_{{v}}}{{\mu }}} {\left( {{{\rho \delta }}U} \right)}}} \right. \kern-0em} {\left( {{{\rho \delta }}U} \right)}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}}.$

Using expression (3) and the fact that ${U \mathord{\left/ {\vphantom {U {{{U}_{s}}}}} \right. \kern-0em} {{{U}_{s}}}} = {{\alpha }} = \frac{7}{8}$ [6], one can get

$${{\left( {{{{{{{\xi }}}_{w}}} \mathord{\left/ {\vphantom {{{{{{\xi }}}_{w}}} 8}} \right. \kern-0em} 8}} \right)}^{{{4 \mathord{\left/ {\vphantom {4 7}} \right. \kern-0em} 7}}}} = \frac{8}{7}{{4}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}}{{\alpha }}_{{v}}^{{{{ - 6} \mathord{\left/ {\vphantom {{ - 6} 7}} \right. \kern-0em} 7}}}{{\left( {{{4{{\rho \delta }}U} \mathord{\left/ {\vphantom {{4{{\rho \delta }}U} {{\mu }}}} \right. \kern-0em} {{\mu }}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 7}} \right. \kern-0em} 7}}}},$$

or

$${{{{\xi }}}_{w}} = 8{{\left( {{8 \mathord{\left/ {\vphantom {8 7}} \right. \kern-0em} 7}} \right)}^{{{7 \mathord{\left/ {\vphantom {7 {24}}} \right. \kern-0em} {24}}}}}{{\alpha }}_{v}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}{{4}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}{{\operatorname{Re} }^{{ - 0.25}}} = {{0.37} \mathord{\left/ {\vphantom {{0.37} {{{{\operatorname{Re} }}^{{0.25}}}}}} \right. \kern-0em} {{{{\operatorname{Re} }}^{{0.25}}}}}.$$

Thus, for the model proposed by the authors

$${{{{\xi }}}_{w}} = \max \left[ {{{64{{{\operatorname{Re} }}^{{ - 1}}}\left( {3{{\alpha }} - 1} \right)} \mathord{\left/ {\vphantom {{64{{{\operatorname{Re} }}^{{ - 1}}}\left( {3{{\alpha }} - 1} \right)} {{\alpha }}}} \right. \kern-0em} {{\alpha }}},\,\,\,\,{{0.37} \mathord{\left/ {\vphantom {{0.37} {{{{\operatorname{Re} }}^{{0.25}}}}}} \right. \kern-0em} {{{{\operatorname{Re} }}^{{0.25}}}}}} \right].$$

SUBSTANTIATION OF THE MODEL

To substantiate the presented model, an analysis of experimental [7–9] and theoretical [7, 10–13] works on liquid film runoff was performed. In most works, the dependence of the dimensionless film thickness ${{{{\delta }}}^{ + }} = \frac{{{\delta }}}{{{\nu }}}\sqrt {{{{{{{\tau }}}_{w}}} \mathord{\left/ {\vphantom {{{{{{\tau }}}_{w}}} {{\rho }}}} \right. \kern-0em} {{\rho }}}}$ (here ${{\nu }}$ is kinematic coefficient of viscosity) from the Reynolds number $\operatorname{Re} = {{4U{{\delta }}} \mathord{\left/ {\vphantom {{4U{{\delta }}} \nu }} \right. \kern-0em} \nu }$ was studied; for the calculation, various ratios were recommended:

$$\begin{gathered} {{{{\delta }}}^{ + }} = {{\left[ {{{{\left( {0.707{{{\operatorname{Re} }}^{{0.5}}}} \right)}}^{{2.5}}} + {{{\left( {0.0379{{{\operatorname{Re} }}^{{0.9}}}} \right)}}^{{2.5}}}} \right]}^{{0.4}}}, \\ \operatorname{Re} = {{4U{{\delta }}} \mathord{\left/ {\vphantom {{4U{{\delta }}} {{{\nu }}\,}}} \right. \kern-0em} {{{\nu }}\,}}\,\,\,[10]; \\ \end{gathered} $$

$${{{{\delta }}}^{ + }} = 0.19{{\operatorname{Re} }^{{0.7}}}\,\,\,\,[7];$$

$$\begin{gathered} {{{{\delta }}}^{ + }} = \left\{ {\frac{{\operatorname{Re} }}{4}\left[ {\frac{{F + {{{\left( {{{\operatorname{Re} } \mathord{\left/ {\vphantom {{\operatorname{Re} } 4}} \right. \kern-0em} 4}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}{{0.5F + 0.333{{{\left( {{{\operatorname{Re} } \mathord{\left/ {\vphantom {{\operatorname{Re} } 4}} \right. \kern-0em} 4}} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}}}} \right.} \right. \\ {{\left. { + \,\,\left. {\frac{{{{\operatorname{Re} } \mathord{\left/ {\vphantom {{\operatorname{Re} } {340}}} \right. \kern-0em} {340}}}}{{\sqrt {{{{\left[ {\ln \left( {10 + {{\operatorname{Re} } \mathord{\left/ {\vphantom {{\operatorname{Re} } {680}}} \right. \kern-0em} {680}}} \right)} \right]}}^{2}} + {{680} \mathord{\left/ {\vphantom {{680} {\operatorname{Re} }}} \right. \kern-0em} {\operatorname{Re} }}} }}} \right]} \right\}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ F = \frac{{{{{{\tau }}}_{c}}}}{{{{\rho }}{{{\left( {g{{\nu }}} \right)}}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}}}\,\,\,\,[11]; \\ \end{gathered} $$

$$\begin{gathered} {{{{\delta }}}^{ + }} = {{\left( {{{\operatorname{Re} } \mathord{\left/ {\vphantom {{\operatorname{Re} } 2}} \right. \kern-0em} 2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,\operatorname{Re} < 1160;\,\,\,\,{{{{\delta }}}^{ + }} = 0.0504{{\left( {\operatorname{Re} } \right)}^{{{7 \mathord{\left/ {\vphantom {7 8}} \right. \kern-0em} 8}}}}, \\ \operatorname{Re} \geqslant 1160\,\,\,\,[12]; \\ \end{gathered} $$

$${{{{\delta }}}^{ + }} = 0.095{{\operatorname{Re} }^{{0.8}}}\,\,\,\,[13].$$

For a liquid film flowing down under the action of gravity, Nusselt obtained the following formula: ${{{{\delta }}}^{ - }} = {{\left( {0.75\operatorname{Re} } \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},$ where ${{{{\delta }}}^{ - }} = {{\delta }}{{\left( {{g \mathord{\left/ {\vphantom {g {{{{{\nu }}}^{2}}}}} \right. \kern-0em} {{{{{\nu }}}^{2}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},$ which can be reduced to the standard form

$${{{{\delta }}}^{ + }} = {{\left( {{{{{\delta }}}^{ - }}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}} = {{\left( {0.75\operatorname{Re} } \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}.$$

The dimensional dependence of the friction coefficient on the Reynolds number is as follows:

$$\begin{gathered} {{{{\tau }}}_{w}} = {{\left( {{{{{\delta }}}^{ + }}} \right)}^{2}}\frac{{{{\rho \nu }}}}{{{\delta }}} = \frac{{128{{{\left( {{{{{\delta }}}^{ + }}} \right)}}^{2}}}}{{{{{\left( {4{{{{\delta }}U} \mathord{\left/ {\vphantom {{{{\delta }}U} \nu }} \right. \kern-0em} \nu }} \right)}}^{2}}}}\frac{{{{\rho }}{{U}^{2}}}}{8} = \frac{{128{{{\left( {{{{{\delta }}}^{ + }}} \right)}}^{2}}}}{{{{{\operatorname{Re} }}^{2}}}}\frac{{{{\rho }}{{U}^{2}}}}{8}, \\ {{\xi }}\left( {\operatorname{Re} } \right) = \frac{{128{{{\left( {{{{{\delta }}}^{ + }}} \right)}}^{2}}}}{{{{{\operatorname{Re} }}^{2}}}}. \\ \end{gathered} $$

The results of comparing the authors’ model with experimental data and data from other authors are shown in Fig. 5, from which it follows that most formulas are applicable only in a certain range of Reynolds numbers and describe the entire range of variation of the Reynolds number with quite acceptable accuracy. The formula presented in this paper has an error close to the rest of the formulas but has a simpler notation and satisfies all the limit transitions at large and small Reynolds numbers.

Fig. 5.

Dependences of the friction coefficient for the movement of the melt (a) under the action of the frictional stress with the gas flow and (b) under the action of gravity of the Reynolds number. 1—Experimental data: (a) [7]; (b) [8, 9]; 2—current model; 3—formula [10]; 4—[11]; 5—[7]; 6—[12]; 7—[13]; 8—Nusselt formula.

CALCULATIONS FOR A TURBULENT FLOW REGIME

Using the developed model and the above formula, calculations were performed for a turbulent film motion, which is characteristic of a high energy release. The velocity in this mode can be found explicitly by the following expression:

$$U = {{\left( {\frac{{4{{\delta }}}}{{{\nu }}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 7}} \right. \kern-0em} 7}}}}{{\left( {\frac{8}{{0.37}}\frac{{\left| {{{{{\tau }}}_{c}} - {{\rho }}g{{\delta }}} \right|}}{{{\rho }}}} \right)}^{{{4 \mathord{\left/ {\vphantom {4 7}} \right. \kern-0em} 7}}}}.$$

The calculation results for large energy releases, taking into account the change in the flow regime, are shown in Fig. 6. The calculations were performed for the values of energy release two, five, seven, and ten times greater than the nominal (N_nom = 450 MW/m³), which corresponds to the hypothetical scenario with a power surge (UTOP accident). As seen from Fig. 6, even with an energy release ten times greater, the nominal Reynolds number does not exceed 6000, and the characteristic time of weight loss due to melting and flowing off of the fuel cladding melt is several seconds. All this suggests that the main type of destruction will be mechanical at high powers, which is characterized by a shorter time for the implementation of this process.

Fig. 6.

Dependences of (a) the calculated Reynolds number and (b) the calculated rate of melt mass loss for steel 316 from time to time. N: 1—2 N_nom; 2—5 N_nom; 3—7 N_nom; 4—10 N_nom.

CONCLUSIONS

(1) The developed models make it possible to calculate the initial stage of an accident, which is accompanied by thermal destruction of a fuel element and movement of the melt under the influence of gravity, viscous forces, and friction with the coolant flow.

(2) Approbation of calculations using the proposed model under various flow conditions showed that the model reliably describes the literature data, including those with a phase transition.

(3) During the accident, the characteristic times of the mass loss of the fuel element cladding are several seconds, and the Reynolds number for the melt does not exceed 6000.