INTRODUCTION

An extensive amount of the literature is devoted to analyzing the separation of liquid mixtures in distillation columns (see [1–7] and others). In this case, one of the central issues is assessing the minimum heat consumption required for the separation process. This consumption determines the complexity of the separation of the mixture at one or another boundary between the fractions separated into the bottom of the column and into a reflux condenser. Heat consumption consists of two components: consumption in a reversible process and additional consumption associated with the irreversibility of heat-transfer processes in the still and reflux condenser and mass transfer along the column height. When the dimensions of the column increase (and, with them, the coefficients of heat and mass transfer), the irreversible component of consumption tends to zero.

At first glance, within the framework of reversible processes, it is impossible to establish a relationship between heat and productivity, since the molar Gibbs separation work depends only on the composition of the mixture being separated and does not reflect properties such as the boiling points of the components. However, this is not the case for processes that use heat. Here, it is required to take into account the coefficient of conversion of heat into work, and this coefficient for a distillation column depends on the temperatures at the bottom of the column and in the reflux condenser, decreasing as these temperatures approach each other. Therefore, in distillation processes, the components of the mixture with close boiling points can be separated only upon significant energy consumption.

We will consider the irreversible estimates of energy consumption for the separation of the mixture in binary distillation; we will show that these estimates, despite being greater than reversible ones, depend on them monotonically. Let us find out in which case the addition of another component (separating agent (SA)) to the initial mixture makes it possible to obtain energy savings.

RELATIONSHIP BETWEEN SYSTEM PARAMETERS AND HEAT CONSUMPTION

The process of separating a multicomponent mixture into two fractions in a distillation column is characterized by the following parameters.

1. Properties of the mixture to be separated: mole fractions of components in the stream being separated \({{x}_{{Fi}}},\) boiling point \(T_{i}^{0}\) and molar heats of vaporization of components \({{r}_{i}},\) \(i = 1, \ldots ,n\) at atmospheric pressure. Below we assume that indices \(i\) increase as the boiling point rises.

2. Product composition: mole fractions of components in a reflux condenser (light fraction) \({{x}_{{Di}}}\) and at the bottom of the column (heavy fraction) \({{x}_{{Bi}}}.\)

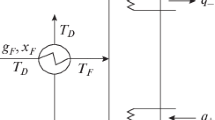
3. Technological parameters of the column: pressure maintained in the column \(\bar {P},\) temperature at the bottom of the column \({{T}_{B}},\) and temperature in the reflux condenser \({{T}_{D}}\) (see Fig. 1).

Fig. 1.
figure 1

Calculation diagram of the distillation column.

Full size image

Under conditions of fixed compositions of the streams at the inlet and outlet of the column, these streams are proportional to each other and any of them can be chosen as the target, in particular, the stream of the mixture being separated \({{g}_{F}}\). In this case, the efficiency of columns means the ratio of the number of moles of the mixture to be separated per unit of consumed heat \({{q}_{ + }}\) supplied to the bottom of the column.

Let us write down the equations of thermodynamic balances of the column—energy, material, and entropy [8, 9]:

$${{g}_{F}}{{x}_{F}} - {{g}_{F}}\varepsilon {{x}_{D}} - {{g}_{F}}(1 - \varepsilon ){{x}_{B}} = 0,$$
(1)
$${{q}_{ + }} - {{q}_{ - }} + {{g}_{F}}{{h}_{F}} - {{g}_{F}}\varepsilon {{h}_{D}} - {{g}_{F}}(1 - \varepsilon ){{h}_{B}} = 0,$$
(2)
$${{g}_{F}}\varepsilon {{s}_{D}} + {{g}_{F}}(1 - \varepsilon ){{s}_{B}} + \frac{{{{q}_{ - }}}}{{{{T}_{D}}}} - {{g}_{F}}{{s}_{F}} - \frac{{{{q}_{ + }}}}{{{{T}_{B}}}} = \sigma \geqslant {{\sigma }_{{{\text{min}}}}}.$$
(3)

Here, \(\sigma > 0\) is the production of entropy in the column; \(h\) is the molar enthalpies of flows; \(s\) is the molar entropies of flows; \(\varepsilon = \frac{{{{x}_{F}} - {{x}_{B}}}}{{{{x}_{D}} - {{x}_{B}}}}\) is the proportion of withdrawal of the top product; and \({{x}_{F}},\) \({{x}_{D}},\) and \({{x}_{B}}\) are the mole fraction of the light fraction, i.e., components whose boiling points are below the selected separation limit, in the corresponding stream.

Assuming that the column is thermally insulated and the heat loss to the environment is much less than the heat flux spent on separation, it can be assumed that \({{q}_{ + }} = {{q}_{ - }} = q.\)

After excluding all variables from these ratios except for the flow rate of the mixture to be separated, the heat flow, and the production of entropy, we obtain an inequality that relates productivity and heat consumption with the value of entropy production:

$$q \geqslant {{g}_{F}}\frac{{{{T}_{B}}}}{{{{T}_{B}} - {{T}_{D}}}}{{A}_{G}} + {{\sigma }_{{{\text{min}}}}}\frac{{{{T}_{B}}{{T}_{D}}}}{{{{T}_{B}} - {{T}_{D}}}},$$
(4)

where \({{A}_{G}}\) is the molar reversible work of separating the mixture, equal to the difference between the molar free energy (chemical potentials) of flows leaving the column and the flow of raw materials

$$\begin{gathered} {{A}_{G}} = - R{{T}_{D}}\left[ {\sum\limits_i {{{x}_{{Fi}}}} \ln {{x}_{{Fi}}}} \right. \\ \left. { - \,\,\varepsilon \sum\limits_i {{{x}_{{Di}}}} \ln {{x}_{{Di}}} - (1 - \varepsilon )\sum\limits_i {{{x}_{{Bi}}}} \ln {{x}_{{Bi}}}} \right]. \\ \end{gathered} $$
(5)

Here, \(\varepsilon \) is the the proportion of the withdrawal of the top product.

Typically, the pressure in the column is selected so that external water can be used to cool the reflux condenser; i.e., the value of \({{T}_{D}}\) was slightly higher than the ambient temperature.

RELATIONSHIP BETWEEN HEAT CONSUMPTION IN REVERSIBLE AND IRREVERSIBLE PROCESSES

As follows from (4), the relationship between the heat consumption and the work of separation in a reversible process is the same as between the power and heat consumption in a reversible heat engine with a Carnot efficiency of

$${{\eta }_{c}} = 1 - \frac{{{{T}_{D}}}}{{{{T}_{B}}}}.$$

Let the laws of heat transfer at the bottom of the column and in the reflux condenser have the form

$$q = {{\beta }_{B}}({{T}_{ + }} - {{T}_{B}}) = {{\beta }_{D}}({{T}_{D}} - {{T}_{ - }}),$$
(6)

where \({{T}_{ + }}\) and \({{T}_{ - }}\) are temperatures of heating steam and cooling liquid; \({{\beta }_{B}}\) and \({{\beta }_{D}}\) are the heat-transfer coefficients at the bottom of the column and in the reflux condenser, respectively; and the kinetics of mass transfer between the vapor and liquid flows in each section of the column is characterized by the expression

$$g(y,{{y}^{0}}) = k\frac{{\left[ {\mu (T,{{y}^{0}}) - \mu (T,y)} \right]}}{T},$$
(7)

where \(y\) is the concentration of the component corresponding to the operating line, \({{y}^{0}}\) is the equilibrium concentration, \(\mu \) is chemical potentials, and \(k\) is the coefficient of mass transfer. Concentrations and temperatures vary from section to section.

For such kinetics, the minimum dissipation depends on the heat flow rate as [9]

$${{\sigma }_{{{\text{min}}}}} = {{q}^{2}}\left( {\left[ {\frac{1}{{{{\beta }_{B}}{{T}_{B}}{{T}_{ + }}}} + \frac{1}{{{{\beta }_{D}}{{T}_{D}}{{T}_{ - }}}}} \right] + \left[ {\frac{{2({{x}_{D}} - {{x}_{B}})}}{{k{{r}^{2}}}}} \right]} \right).$$
(8)

After substituting this expression into (4), we can reduce this inequality, which determines the boundary of the region of the implemented column modes, to the following form:

$${{g}_{F}} \leqslant bq - a{{q}^{2}},$$
(9)

where \(b\) and \(a\) are characteristic parameters related to column parameters as

$$a = \left[ {\frac{1}{{{{\beta }_{B}}{{T}_{B}}{{T}_{ + }}}} + \frac{1}{{{{\beta }_{D}}{{T}_{D}}{{T}_{ - }}}} + \frac{{2({{x}_{D}} - {{x}_{B}})}}{{k{{r}^{2}}}}} \right]\frac{{{{T}_{D}}}}{{{{A}_{G}}}},$$
(10)
$$b = \frac{{{{\eta }_{c}}}}{{{{A}_{G}}}} = \frac{{{{T}_{D}}}}{{{{A}_{G}}{{K}_{T}}}}.$$
(11)

Here, \({{K}_{T}}\) is the temperature coefficient:

$${{K}_{T}} = \frac{{{{T}_{B}}{{T}_{D}}}}{{{{T}_{B}} - {{T}_{D}}}}.$$
(12)

The efficiency of the column (heat consumption per mole of the mixture to be separated), corresponding to the boundary of the region of feasibility, expressed in terms of the characteristic parameters, will take the following form:

$$\eta = \frac{{{{g}_{F}}}}{q} = b - aq.$$
(13)

From (13) it follows that the efficiency reaches a maximum equal to \(b\) in a reversible process when \({{g}_{F}}\) and \(q\) tend to zero.

The working section of the boundary of the feasibility region corresponds to those values \(q\) at which productivity does not decrease with increasing heat consumption. It is limited in value \(q^{*} = \frac{b}{{2a}}.\) The efficiency at the working area decreases linearly from \(b\) to \(b{\text{/}}2.\)

We introduce the relative heat flow rate \({{q}^{0}} = {q \mathord{\left/ {\vphantom {q {q{\text{*}}}}} \right. \kern-0em} {q{\text{*}}}}.\) In the working section, \({{q}^{0}}\) varies from zero to one. Column efficiency as a function of \({{q}^{0}}\) is

$$\eta = b(1 - 0.5{{q}^{0}}).$$
(14)

So, if the value of reversible efficiency \(b\) in one column is larger than in another, this inequality remains for the efficiency of the column in the class of irreversible processes in the entire working area.

CALCULATION OF TEMPERATURES AT THE BOTTOM OF THE COLUMN AND IN THE DEFLEGMATOR

In practice, the temperature in the reflux condenser is usually set approximately equal to \({{T}_{D}} = 323\;{\text{K}}{\text{,}}\) so that water can be used as a coolant at an ambient temperature of about 300 K.

The compositions of the vapor phase \({{y}_{D}}\) and liquid phase \({{x}_{D}}\) in the reflux condenser are related to each other by the phase equilibrium constants \({{K}_{{iD}}},\) which depend on the properties of the \(i\)th component, temperature \({{T}_{D}}\), and pressure \(\bar {P}\) in a dephlegmator:

$${{y}_{{Di}}} = {{x}_{{Di}}}{{K}_{{iD}}}({{T}_{D}},\bar {P}).$$

Since the mole fraction of each of the components in the vapor in equilibrium is equal to the ratio of the partial pressure of this component \({{P}_{{iD}}}\) to the total pressure \(\bar {P},\) then

$${{K}_{{iD}}}({{T}_{D}},\bar {P}) = \frac{{P_{i}^{0}({{T}_{D}})}}{{\bar {P}}}.$$
(15)

Partial pressure \({{P}_{{iD}}}({{T}_{D}})\) is the product of the vapor pressure of the pure component \(P_{{iD}}^{0}({{T}_{D}})\) and the mole fraction of this component in the liquid.

Consider the equilibrium of the vapor-liquid mixture at the top of the column. The composition of the stream leaving the reflux condenser is determined by the composition of the vapor \(y\) in the vapor-liquid mixture. The composition of the liquid at the top of the column depends on \(y,\) pressure \(\bar {P}\), and temperature \({{T}_{D}}\) as

$${{x}_{D}} = \frac{{{{y}_{D}}}}{{{{K}_{D}}({{T}_{D}},\bar {P})}}.$$
(16)

Since \(\sum\limits_i {{{x}_{{Di}}}} = 1\), from (15), (16) we can express \(\bar {P}\) through \({{x}_{D}}{\text{:}}\)

$$\bar {P} = \frac{1}{{\sum\limits_{i = 1}^n {\frac{{{{x}_{{Di}}}}}{{P_{i}^{0}({{T}_{D}})}}} }}.$$
(17)

Similarly, knowing the pressure in the column \(\bar {P},\) composition, and properties of components at the bottom of the column we can find the temperature at the bottom of the column \({{T}_{B}}\) from the equation of vapor-liquid equilibrium for the bottom product:

$$\bar {P} = \sum\limits_{i = 1}^n {{{x}_{{Bi}}}P_{i}^{0}({{T}_{B}})} .$$
(18)

The resulting equation in the overwhelming majority of cases can be solved with respect to \({{T}_{B}}\) only numerically, but, due to the fact that its right-hand side increases monotonically with increasing \({{T}_{B}},\) it has only one valid root.

If the fractions are ideal solutions, then the Antoine equation can be used to calculate the vapor pressures of each of the components [11]:

$$P_{i}^{0}(T) = {{10}^{{\left( {{{A}_{i}} - \frac{{{{B}_{i}}}}{{T + {{C}_{i}}}}} \right)}}},$$
(19)

where \({{A}_{i}},\) \({{B}_{i}}\), and \({{C}_{i}}\) are empirical coefficients, tables for which are available for most substances. In the case of imperfect fractions, it is necessary to use more complex dependences of the saturated vapor pressure of the component on the temperature and its mole fraction in the liquid [7].

Thus, the algorithm for calculating the temperatures at the bottom of the column and in the reflux condenser is as follows.

1. Set the temperature in the column reflux condenser \({{T}_{D}},\) stream compositions \({{x}_{F}},\) \({{x}_{D}},\) and \({{x}_{B}}\) and the corresponding coefficients of the Antoine equation \({{A}_{i}},\) \({{B}_{i}},\) and \({{C}_{i}}\) for each component.

2. The pressure that must be maintained in the column is calculated so that, at a given composition, temperature \({{T}_{D}}\) took the desired value using the equation of vapor-liquid equilibrium in the column reflux condenser (17). The required values of vapor pressures for each of the components are found from Antoine equation (19).

3. Numerically solve vapor-liquid equilibrium equation (18) for the boiling point at the bottom of the column \({{T}_{B}}\).

Example 1. Two-component mixture. Consider the separation of the mixture, the data on which are given in Table 1 [7, 12].

Table 1.   Data on the mixture and separation products for example 1
Full size table

1. The temperature in the reflux condenser is set and equal to \({{T}_{D}} = 323\;{\text{K}}{\text{.}}\) The properties of the mixture to be separated and the separation products are presented in Table. 1.

2. Let us find the partial pressures of pure components using expression (19):

$$\begin{gathered} P_{1}^{0}({{T}_{D}}) = {{10}^{{\left( {4.01814 - \frac{{1203.835}}{{323 + 53.226}}} \right)}}} = 6.58, \\ P_{2}^{0}(T) = {{10}^{{\left( {4.07827 - \frac{{1343.943}}{{323 + 53.773}}} \right)}}} = 3.25. \\ \end{gathered} $$

According to formula (17), the total pressure in the column is

$$\bar {P} = \frac{1}{{\frac{{0.95}}{{6.58}} + \frac{{0.05}}{{3.25}}}} = 6.26.$$

3. Let us compose the equation of vapor-liquid equilibrium for the bottom of the column (see (18)) and determine the temperature at the bottom of the column:

$$\begin{gathered} 6.26 = 0.1 \times {{10}^{{\left( {4.01814 - \frac{{1203.835}}{{{{T}_{B}} + 53.226}}} \right)}}} + 0.9 \\ \times \,\,{{10}^{{\left( {4.07827 - \frac{{1343.943}}{{{{T}_{B}} + 53.773}}} \right)}}}. \\ \end{gathered} $$

Solving this equation numerically, we obtain the value \({{T}_{B}} = 351\;{\text{K}}{\text{.}}\)

4. The reversible efficiency \({{\eta }_{c}}\) is

$${{\eta }_{c}} = \frac{{351 - 323}}{{351}} = 0.08.$$

Thus, the reversible efficiency of the distillation column is very low, and in the mode of maximum productivity it will be 4%.

Example 2. Multicomponent mixture. Consider the process of separating the mixture, data on which are given in Table 2 [7, 12]. The separation boundary is between propane and n-butane. Find the temperature coefficient for the selected separation option using the above algorithm.

Table 2.   Data on the mixture and separation products for example 2
Full size table

1. The temperature in the reflux condenser is set and equal to \({{T}_{D}} = 323\;{\text{K}}{\text{.}}\) The properties of the mixture to be separated and the separation products are presented in Table 2.

2. The pressure to be set in the column is found from Eq. (17):

$$\bar {P} = 36.35.$$

3. From (18), after its numerical solution, similarly to example 1, we find the temperature at the bottom of the column:

$${{T}_{B}}{\text{ = }}425\;{\text{K}}.$$

4. The reversible efficiency is

$${{\eta }_{c}} = 1 - \frac{{323}}{{425}} = 0.24.$$

EXPEDIENCY OF USING A SEPARATING AGENT

In distillation processes for separating substances with close boiling points or azeotropes, schemes with an SA are used [14]. In this case, the SA is added to the mixture to be separated, having a boiling point lower (azeotropic distillation) or higher (extractive distillation) than the components of the mixture to be separated. The resulting three-component mixture is separated in a cascade of two columns. In the first of them, the mixture of SA is separated with a component close to it in terms of boiling point and, in the second, this mixture is separated, returning the SA to the system inlet. Figures 2 and 3 show schemes of extractive and azeotropic distillation.

Fig. 2.
figure 2

Scheme of extractive distillation of a two-component mixture.

Full size image
Fig. 3.
figure 3

Scheme of azeotropic distillation of a two-component mixture.

Full size image

The thermodynamic analysis of such systems [14] makes it possible to find out at a qualitative level under what conditions the addition of an SA reduces the heat consumption for the separation of 1 mole of the mixture.

The use of SA may be advisable not only for azeotropic mixtures, but also for difficult-to-separate substances with similar physicochemical properties. In this case, it is necessary to compare heat consumption in the system with an SA from two columns and a mixer with heat consumption in one column with low-boiling components. Using the above relations arising from thermodynamic balances, we will find out under what conditions the use of an SA will lead to thermal energy saving per mole of the mixture to be separated in a reversible approximation. Due to the monotonic dependence of heat consumption in an irreversible process on its consumption in a reversible process, this condition will make it possible to assess the expediency of using an SA even for a given nonzero productivity.

Let us consider in more detail extractive distillation, and we will give similar relationships for azeotropic distillation without derivation.

Comparison of reversible heat consumption for extractive distillation. Let us denote by \(\varepsilon \) the number of moles of SA added per mole of the initial mixture (degree of dilution) through \({{\eta }_{{c0}}},\) \({{\eta }_{{c1}}},\) \({{\eta }_{{c2}}}\)—the reversible efficiency of the column separating the initial mixture, a mixture of three components with the SA in the first column of the cascade, and a mixture of the SA with the component with the closest boiling point in the second column.

The condition for the expediency of using the SA in these designations will take the following form:

$$\frac{{({{x}_{1}} + \varepsilon ){{A}_{{G1}}}}}{{{{\eta }_{{c1}}}}} + \frac{{({{x}_{2}} + \varepsilon ){{A}_{{G2}}}}}{{{{\eta }_{{c2}}}}} < \frac{{{{A}_{{G0}}}}}{{{{\eta }_{{c0}}}}}.$$
(20)

Here, \({{x}_{1}}\) is the mole fraction of the low-boiling component in the initial mixture, \({{x}_{2}}\) is the mole fraction of the high-boiling component, and \({{x}_{2}} = 1 - {{x}_{1}}.\) On the left and right sides of this inequality, there is reversible heat consumption per mole of the initial mixture. The molar work of separation is

$${{A}_{{G1}}} = - R{{T}_{D}}\left( {\frac{{{{x}_{1}}}}{{1 + \varepsilon }}\ln \frac{{{{x}_{1}}}}{{1 + \varepsilon }} + \frac{{{{x}_{2}} + \varepsilon }}{{1 + \varepsilon }}\ln \frac{{{{x}_{2}} + \varepsilon }}{{1 + \varepsilon }}} \right).$$
(21)

Similarly,

$${{A}_{{G2}}} = - R{{T}_{D}}\left( {\frac{{{{x}_{2}}}}{{{{x}_{2}} + \varepsilon }}\ln \frac{{{{x}_{2}}}}{{{{x}_{2}} + \varepsilon }} + \frac{\varepsilon }{{{{x}_{2}} + \varepsilon }}\ln \frac{\varepsilon }{{{{x}_{2}} + \varepsilon }}} \right),$$
(22)
$${{A}_{{G0}}} = - R{{T}_{D}}\left( {{{x}_{1}}\ln {{x}_{1}} + {{x}_{2}}\ln {{x}_{2}}} \right).$$
(23)

It is easy to see that the substitution of these expressions into inequality (20), after reducing the left and right sides of the inequality by \(R{{T}_{D}}\), yields

$$\begin{gathered} - \frac{{{{x}_{1}}\ln {{x}_{1}} + ({{x}_{2}} + \varepsilon )\ln ({{x}_{2}} + \varepsilon ) - (1 + \varepsilon )\ln (1 + \varepsilon )}}{{{{\eta }_{{c1}}}}} \\ - \,\,\frac{{{{x}_{2}}\ln {{x}_{2}} + \varepsilon \ln \varepsilon - ({{x}_{2}} + \varepsilon )\ln ({{x}_{2}} + \varepsilon )}}{{{{\eta }_{{c2}}}}} \\ < - \frac{{{{x}_{1}}\ln {{x}_{1}} + {{x}_{2}}\ln {{x}_{2}}}}{{{{\eta }_{{c0}}}}}. \\ \end{gathered} $$
(24)

Taking into account the independence of the boiling point ratio from the pressure in the column, the thermal reversible efficiency is

$${{\eta }_{{c0}}} = 1 - \frac{{{{T}_{1}}}}{{{{T}_{2}}}},\,\,\,\,{{\eta }_{{c1}}} = 1 - \frac{{{{T}_{1}}}}{{{{T}_{{2s}}}(\varepsilon )}},\,\,\,{{\eta }_{{c2}}} = 1 - \frac{{{{T}_{2}}}}{{{{T}_{s}}}}.$$
(25)

Here, \({{T}_{s}}\) is the boiling point of SA, \({{T}_{{2s}}}\) is the boiling point of the mixture of the second component and SA, and \({{T}_{2}}\) is the boiling point of the second component at atmospheric pressure.

The following inequalities are valid:

$${{T}_{1}} < {{T}_{2}} < {{T}_{{2s}}} < {{T}_{s}}.$$

The sum of the expressions in the numerators of the fractions on the left side of inequality (24) is greater than \({{A}_{{G0}}},\) since the scheme with an SA contains a mixer and additional separation work is required to separate the mixed streams in it.

Comparison of reversible heat consumption for azeotropic distillation. For this type of distillation, we have \({{T}_{s}} < {{T}_{{1s}}} < {{T}_{1}} < {{T}_{2}},\) and the expressions for reversible separation works (21), (22) will be rewritten as follows:

$${{A}_{{G1}}} = - R{{T}_{D}}\left( {\frac{{{{x}_{1}} + \varepsilon }}{{1 + \varepsilon }}\ln \frac{{{{x}_{1}} + \varepsilon }}{{1 + \varepsilon }} + \frac{{{{x}_{2}}}}{{1 + \varepsilon }}\ln \frac{{{{x}_{2}}}}{{1 + \varepsilon }}} \right),$$
(26)
$${{A}_{{G2}}} = - R{{T}_{D}}\left( {\frac{{{{x}_{1}}}}{{{{x}_{1}} + \varepsilon }}\ln \frac{{{{x}_{1}}}}{{{{x}_{1}} + \varepsilon }} + \frac{\varepsilon }{{{{x}_{1}} + \varepsilon }}\ln \frac{\varepsilon }{{{{x}_{1}} + \varepsilon }}} \right).$$
(27)

The condition for the expediency of using an SA, like in (24), for azeotropic distillation takes the form

$$\begin{gathered} - \frac{{{{x}_{2}}\ln {{x}_{2}} + ({{x}_{1}} + \varepsilon )\ln ({{x}_{1}} + \varepsilon ) - (1 + \varepsilon )\ln (1 + \varepsilon )}}{{{{\eta }_{{c1}}}}} \\ - \,\,\frac{{{{x}_{1}}\ln {{x}_{1}} + \varepsilon \ln \varepsilon - ({{x}_{1}} + \varepsilon )\ln ({{x}_{1}} + \varepsilon )}}{{{{\eta }_{{c2}}}}} \\ < - \frac{{{{x}_{1}}\ln {{x}_{1}} + {{x}_{2}}\ln {{x}_{2}}}}{{{{\eta }_{{c0}}}}}. \\ \end{gathered} $$
(28)

Here,

$${{\eta }_{{c0}}} = 1 - \frac{{{{T}_{D}}}}{{{{T}_{2}}}},\,\,\,\,{{\eta }_{{c1}}} = 1 - \frac{{{{T}_{D}}}}{{{{T}_{2}}(\varepsilon )}},\,\,\,\,{{\eta }_{{c2}}} = 1 - \frac{{{{T}_{D}}}}{{{{T}_{1}}}},$$

where \(\widehat {{{T}_{2}}}(\varepsilon )\) is the boiling point of the second component when choosing a pressure in the column for which the temperature of the mixture of the first component with the SA has a given value \({{T}_{D}};\) \({{T}_{1}}\) is the boiling point of the first component at a pressure in the column that provides a boiling point of the SA equal to \({{T}_{D}}.\)

Due to the fact that the ratio of boiling points depends little on pressure, in expressions for \(\eta \) we can use the ratio of boiling points at atmospheric pressure; then

$${{\eta }_{{c0}}} = 1 - \frac{{{{T}_{1}}}}{{{{T}_{2}}}},\,\,\,\,{{\eta }_{{c1}}} = 1 - \frac{{{{T}_{{1s}}}(\varepsilon )}}{{{{T}_{2}}}},\,\,\,\,{{\eta }_{{c2}}} = 1 - \frac{{{{T}_{s}}}}{{{{T}_{1}}}}.$$
(29)

Example 3. Let us consider the azeotropic separation of a water–pyridine mixture [15] with concentrations of 0.51 and 0.49, respectively. Boiling points of components are as follows: water, \({{T}_{1}} = 373\;{\text{K}}{\text{,}}\) pyridine, \({{T}_{2}} = 388\;{\text{K}}{\text{.}}\) As an SA, we use methanol with \({{T}_{s}} = 338\;{\text{K}}{\text{,}}\) which forms a mixture with water, boiling at a temperature \({{T}_{{1s}}} = 353\;{\text{K}}\) with a molar ratio of 14 : 86 [16]. Thus, we need to add \(\varepsilon = 0.16{{x}_{1}} = 0.082\) mole of methanol to one mole of a water–pyridine mixture with mole fractions of water \({{x}_{1}}\) and pyridine \({{x}_{2}}\).

Let us calculate thermal efficiency according to formulas (29):

$$\begin{gathered} {{\eta }_{{c0}}} = 1 - \frac{{373}}{{388}} = 0.039,\,\,\,\,{{\eta }_{{c1}}} = 1 - \frac{{353}}{{388}} = 0.08, \\ {{\eta }_{{c2}}} = \frac{{338}}{{353}} = 0.042 \\ \end{gathered} $$

and substitute it into inequality (28). We obtain

$$\begin{gathered} \frac{{0.35 + 0.31 + 0.085}}{{0.08}} + \frac{{0.343 + 0.205 - 0.31}}{{0.042}} \\ < \frac{{0.343 + 0.35}}{{0.039}}. \\ \end{gathered} $$

The left side of this inequality is 15 and the right side is 17.8. Relative savings E amounted to 16%.

Assuming that the degree of SA dilution and all thermal efficiencies are fixed, we plot the dependence of the percentage of energy savings on the composition of the initial mixture. The graph of this function is shown in Fig. 4. It can be seen that the addition of methanol in a molar ratio of 14 : 86 (mass ratio approximately 5 : 18) to water is advisable when the mole fraction of water in the initial mixture \({{x}_{1}} < 0.78.\)

Fig. 4.
figure 4

Dependence of energy savings on the composition of the mixture. In the shaded area, the use of an SA is advisable.

Full size image

CONCLUSIONS

Equations are obtained that define the boundary of the region of possible modes of a binary distillation column with a given productivity. Reversible heat consumption depends on the separation order due to the fact that the thermal efficiency of the column depends on it. It is shown that heat consumption per mole of the mixture being separated, taking into account irreversibility, monotonically depends on reversible consumption, which makes it possible to use reversible indicators for choosing the separation order. The conditions under which the use of an SA allows one to obtain energy saving are given.

NOTATION

\({{A}_{G}}\)

molar work of separation, J/mol

\(a\)

irreversibility coefficient

\(b\)

reversible efficiency

\({{g}_{F}}\)

flow rate of the mixture to be separated, mol/s

\({{h}_{F}},\) \({{h}_{D}},\) \({{h}_{B}}\)

molar enthalpies of flows, J/mol

\({{K}_{D}}\)

phase equilibrium constant

\({{K}_{T}}\)

temperature coefficient

\(k\)

mass-transfer coefficient

\(P\)

partial pressure, Pa

\({{P}^{0}}\)

vapor pressure of the pure component, Pa

\(\bar {P}\)

column pressure, Pa

\({{q}_{ + }},\) \({{q}_{ - }},\) \(q\)

heat flow rates, W

\({{r}_{i}}\)

molar heat of vaporization of the \(i\)th component, kJ/mol

\({{s}_{F}},\) \({{s}_{D}},\) \({{s}_{B}}\)

molar entropy of flows, J/(mol K)

\({{T}_{B}}\)

temperature at the bottom of the column, K

\({{T}_{D}}\)

temperature in the reflux condenser, K

\({{T}_{i}}\)

boiling temperature of the \(i\)th component, K

\({{x}_{{Bi}}}\)

mole fraction of the \(i\)th component at the bottom of the column (heavy fraction)

\({{x}_{{Di}}}\)

mole fraction of the \(i\)th component in a reflux condenser (light fraction)

\({{x}_{{Fi}}}\)

mole fraction of the \(i\)th component in the mixture to be separated

\({{y}^{0}}\)

equilibrium concentration

\(\alpha \)

relative volatility

\({{\beta }_{D}},\) \({{\beta }_{B}}\)

heat-transfer coefficients in a reflux condenser and at the bottom of the column, W/K

\(\varepsilon \)

dilution ratio of the SA

\(\eta \)

thermal efficiency

\(\sigma \)

entropy production, W/K