INTRODUCTION

Nowadays, the uncontrolled discharge of heavy metal ions has become a major problem. Lead is one of the toxic heavy metals which can result in significant environmental issues and can pose a severe threat to the public health [1–6]. Different methods have been used for heavy metals removal from aqueous solutions such as precipitation, ion exchange, electrolysis, reverse osmosis, bioremediation and adsorption. Among these methods, adsorption has been widely used for water and wastewater treatment due to its relatively low cost and simple operation and also easily available adsorbents such as natural zeolites [7–9].

Magnetic composite adsorbents can be easily separated from the solution by an external magnetic field and, therefore, would remove heavy metals in perfect performance [10–13]. Magnetic composite adsorbents, including magnetite nanoparticles, functionalized or modified with some compounds as zeolites, have specific chemical, physical and surface properties that allow selective ions removal [14–16].

Adsorption studies in batch adsorption systems give important equilibrium and kinetics data useful for the prediction of further industrial adsorption system performance [17]. For estimating the parameters for wider operating conditions and optimal design of adsorption systems, it is important to have accurate modeling of dynamics, kinetics and equilibrium behavior. Several proper assumptions have been considered in mathematical models to reduce the complexity of the computational work while resulting in the predictions which are in a relatively good agreement with experimental data. For accurate modeling of the adsorption process, it is necessary to incorporate external mass transfer into the solid phase diffusion model. The objective of this work was to develop a homogeneous diffusion model combined with external mass transfer resistance, which could be used for the evaluation of the kinetics of lead adsorption onto the modified natural zeolite. The proposed mathematical model was solved using the finite difference method and COMSOL Multiphysics code. The internal effective diffusivity as the process parameter was determined for different concentrations of the solution using which a parametric study has been carried out to study the effects of particle size of adsorbent, initial adsorbate concentration, solution volume and the amount of absorbent on the adsorption kinetics.

Table 1.   Specification of the adsorbent
Full size table

EXPERIMENTS

The natural zeolite (clinoptilolite), as a wide spread mineral, was collected from central Alborz Mountains, Iran, with elemental composition KNa2Ca2(Al7Si29)O72 ⋅ 24H2O. All the other chemical reagents were of an analytical reagent grade.

The clinoptilolite powder was added to distilled water and was homogenized using mechanical stirring. The solutions of FeCl2 ⋅ 4H2O and FeCl3 ⋅ 6H2O in water with a molar ratio of 1 : 2 were mixed and then were deoxygenated by bubbling of argon gas. Sodium hydroxide solution was added dropwise to the suspension while the mixture was vigorously mechanical stirred under an ultrasonic irradiation and in argon atmosphere. After the precipitation of magnetite on the zeolite, the prepared composite was separated using a magnet, was washed with distilled water for four times and then was dried. The prepared composite was dispersed into a transparent suspension which initial pH was adjusted to about 11. The glutaraldehyde solution as a crosslinker was dropped to the suspension with a stirring under the ultrasonic irradiation. Next, a solution of chitosan in an acetic acid was added dropwise to the suspension while the mixture was vigorously mechanically stirred under ultrasonic irradiation. After the addition was completed, the final composite (adsorbent) was separated using a magnetic field, washed and then dried.

Scanning electron microscopy (SEM) (Cam-Scan MV 2300) was used to study the surface of the adsorbent. The lead concentration in the solution was determined using an atomic absorption spectrophotometer (Buck 210VGP). The surface area (BET) was measured by the nitrogen adsorption at 77 K using a nitrogen adsorption analysis instrument (Sensiran Co.). A stock lead ion solution of 1000 mg/L was prepared by dissolving 1.5980 g of lead nitrate into a 1000 mL of deionized water and the solution was diluted for different considered ion concentrations. The pH of the solutions was adjusted by adding 1 M NaOH and 1 M HNO3 solutions.

THEORY AND MATHEMATICAL MODELING

In the mass transfer models, it is required to define the relationships of the solid/liquid equilibrium, the mass balance equation, and diffusional mass transport [18]. The assumptions made for deriving the equations for this model are the following: (a) the adsorbent particle is considered as a homogeneous sphere solid, (b) the pseudo-steady-state approximation is valid, (c) the local equilibrium occurs only at the external surface of the adsorbent particle and (d) the liquid-diffusion resistance occurs at the external surface of the adsorbent particle as film transfer.

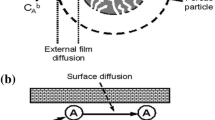
The schematic of the adsorption process in our model is illustrated in Fig. 1. After transferring the adsorbate ions from the bulk solution into the absorbent surface, they are then transferred through the adsorbent particles.

Fig. 1.
figure 1

Lead concentration profiles in the bulk liquid and the adsorbent particle and the SEM image of the adsorbent particles.

Full size image

Such a process can be mathematically described by Fick’s second law of diffusion. In spherical coordinates, the mass balance equation is expressed as

$$\frac{{{{D}_{{{\text{eff}}}}}}}{{{{r}^{2}}}}\frac{\partial }{{\partial r}}\left( {{{r}^{2}}\frac{{\partial {{q}_{t}}}}{{\partial r}}} \right) = \frac{{\partial {{q}_{t}}}}{{\partial t}}~,\,\,0 \leqslant r \leqslant R,\,\,t > 0,$$
((1))

where qt is the lead (solute) concentration in the adsorbent particle and \({{D}_{{{\text{eff}}}}}\) is the lead effective diffusivity which is assumed to be constant during the adsorption process. The diffusion equation can be simplified by taking the lead concentration in the adsorbent to be parabolic with respect to the spherical adsorbent radius [19–22], that is

$${{q}_{t}} = ~{{a}_{0}} + {{a}_{2}}{{r}^{2}},$$
((2))

where a0 and a2 are dependent only on time for this case. A known volume of the lead solution, V, of the lead concentration C, was contacted with a known volume Vp of the adsorbent. Diffusion takes place into the adsorbent particle according to Eq. (1), followed by the equilibrium adsorption between the adsorbent surface and the surrounding liquid. In case of applying the Langmuir isotherm model for the equilibrium

$${{q}_{e}} = \frac{{{{q}_{m}}{{K}_{L}}{{C}_{e}}}}{{1 + {{K}_{L}}{{C}_{e}}}}~\,\, \to ~\,\,{{C}_{e}} = \frac{{{{q}_{e}}}}{{{{K}_{L}}\left( {{{q}_{m}} - {{q}_{e}}} \right)}}~,$$
((3))

where qe, KL and qm are the lead concentration in the adsorbent particle at the equilibrium, the Langmuir adsorption constant and the maximum capacity of the adsorbent, respectively. It assumed that the liquid-diffusion resistance occurs at the external surface of the adsorbent particle as film transfer, so that mass transfer from the external liquid phase can be expressed as

$$\begin{gathered} {{D}_{{{\text{eff}}}}}\frac{{\partial {{q}_{t}}}}{{\partial r}} = {{K}_{f}}\left( {C - {{C}_{e}}} \right) \\ = \,\,~{{K}_{f}}\left( {C - \frac{{{{q}_{e}}}}{{{{K}_{L}}\left( {{{q}_{m}} - {{q}_{e}}} \right)}}} \right),\,\,r = R. \\ \end{gathered} $$
((4))

The external mass transfer coefficient, Kf, for the lead adsorbed can be obtained by

$${{K}_{f}} = - \frac{{{{R}_{p}}{{\rho }_{p}}V}}{{3mt}}{\text{ln}}\left( {\frac{C}{{{{C}_{0}}}}} \right),$$
((5))

where C0 is the initial lead concentration and R, m and ρp are the particle radius, mass and density, respectively [23]. The lead effective diffusivity \({{D}_{{{\text{eff}}}}},\) can be obtained by fitting the modeling results and the batch experimental data. The mass balance of the lead ions between the solution and the adsorbent can be expressed as

$$\begin{gathered} V\frac{{dC}}{{dt}} = ~ - {{D}_{{{\text{eff}}}}}\frac{{\partial {{q}_{t}}}}{{\partial r}}A = ~\, - {{V}_{p}}\frac{{d\overline {{{q}_{t}}} }}{{dt}} \\ \xrightarrow{{{\text{integration}}}}\,\,~~\overline {{{q}_{t}}} = \,\,~{{q}_{0}} - \frac{V}{{{{V}_{p}}}}\left( {C - {{C}_{0}}} \right), \\ \end{gathered} $$
((6))

where q0 is the initial lead concentration in the adsorbent particle, A is the total interfacial area for the adsorbent particles and the solution, and \(\overline {{{q}_{t}}} \) is the average of the lead concentration in the adsorbent particle which is given by

$$\begin{gathered} \overline {{{q}_{t}}} = \frac{{\int\limits_0^R {{{q}_{t}}4\pi rh2} dr}}{{\frac{{4\pi {{R}^{3}}}}{3}}}~\, \to \frac{{d\overline {{{q}_{t}}} }}{{dt}} = \frac{{3\int\limits_0^R {\frac{{\partial {{q}_{t}}}}{{\partial t}}{{r}^{2}}dr} }}{{{{R}^{3}}}} \\ = \,\,\frac{{3{{D}_{{{\text{eff}}}}}}}{R}\frac{{\partial {{q}_{t}}}}{{\partial r}} \\ \end{gathered} $$
((7))

Considering Eq. (2) at r = R,\(\overline {{{q}_{t}}} ~\)reduces to the following equation:

$$\begin{gathered} {{q}_{t}} = {{a}_{0}} + {{a}_{2}}{{R}^{2}}~, \\ ~\frac{{\partial {{q}_{{t~}}}}}{{\partial r}}~ = 2{{a}_{2}}R \to \overline {{{q}_{t}}} = \frac{{\int\limits_0^R {{{q}_{t}}4\pi {{r}^{2}}dr} }}{{\frac{{4\pi {{R}^{3}}}}{3}}} \\ = \,\,\frac{{3\int\limits_0^R {({{a}_{0}} + {{a}_{2}}{{R}^{2}})} {{r}^{2}}dr}}{{{{R}^{3}}}} = {{a}_{0}} + \frac{3}{5}{{a}_{2}}{{R}^{2}}. \\ \end{gathered} $$
((8))

From Eq. (8), the parabolic profile assumption at r = R leads to

$$\frac{{\partial {{q}_{t}}}}{{\partial r}} = ~\frac{5}{R}\left( {{{q}_{e}} - \overline {{{q}_{t}}} ~} \right).$$
((9))

Combining Eqs. (4) and (9), a general result is obtained which provides the relation between the bulk solution, the surface and the average lead concentration in the adsorbent particles as follows

$$\overline {{{q}_{t}}} = {{q}_{e}} - \frac{{{{K}_{f}}R}}{{5{{D}_{{{\text{eff}}}}}}}\left( {C - \frac{{{{q}_{e}}}}{{{{K}_{L}}\left( {{{q}_{m}} - {{q}_{e}}} \right)}}} \right).$$
((10))

Since the lead concentration in the liquid C is the only easily measurable parameter of Eq. (10), we eliminated qe by combining Eqs. (4) and (7):

$$\frac{{d\overline {{{q}_{t}}} }}{{dt}} = \frac{{3{{K}_{f}}}}{R}\left( {C - \frac{{{{q}_{e}}}}{{{{K}_{L}}\left( {{{q}_{m}} - {{q}_{e}}} \right)}}} \right).$$
((11))

Substituting \({{q}_{e}}\) from Eq. (11) into Eq. (10), Eq. (10) can be written in terms of C and \(\overline {{{q}_{t}}} \):

$$\begin{gathered} {{q}_{e}} = \frac{{{{q}_{m}}{{K}_{L}}\left( {C - \frac{R}{{3{{K}_{f}}}}\frac{{d\overline {{{q}_{t}}} }}{{dt}}} \right)}}{{\left( {C - \frac{R}{{3{{K}_{f}}}}\frac{{d\overline {{{q}_{t}}} }}{{dt}}} \right)}} \to \overline {{{q}_{t}}} = \frac{{{{q}_{m}}{{K}_{L}}\left( {C - \frac{R}{{3{{K}_{f}}}}\frac{{d\overline {{{q}_{t}}} }}{{dt}}} \right)}}{{\left( {C - \frac{R}{{3{{K}_{f}}}}\frac{{d\overline {{{q}_{t}}} }}{{dt}}} \right)}} \\ - \,\,\frac{{{{K}_{m}}R}}{{5{{D}_{{{\text{eff}}}}}}}\left( {C - \frac{{\frac{{{{q}_{m}}{{K}_{L}}\left( {C - \frac{R}{{3{{K}_{f}}}}\frac{{d\overline {{{q}_{t}}} }}{{dt}}} \right)}}{{1 + {{K}_{L}}\left( {C - \frac{R}{{3{{K}_{f}}}}\frac{{d\overline {{{q}_{t}}} }}{{dt}}} \right)}}}}{{{{K}_{L}}\left( {{{q}_{m}} - \frac{{{{q}_{m}}{{K}_{L}}\left( {C - \frac{R}{{3{{K}_{f}}}}\frac{{d\overline {{{q}_{t}}} }}{{dt}}} \right)}}{{1 + {{K}_{L}}\left( {C - \frac{R}{{3{{K}_{f}}}}\frac{{d\overline {{{q}_{t}}} }}{{dt}}} \right)}}} \right)}}} \right). \\ \end{gathered} $$
((12))

After some simplification, Eq. (12) reduces to

$$\overline {{{q}_{t}}} = \frac{{{{q}_{m}}{{K}_{L}}\left( {C - \frac{R}{{3{{K}_{f}}}}\frac{{d\overline {{{q}_{t}}} }}{{dt}}} \right)}}{{1 + {{K}_{L}}\left( {C - \frac{R}{{3{{K}_{f}}}}\frac{{d\overline {{{q}_{t}}} }}{{dt}}} \right)}} - \frac{{{{R}^{2}}}}{{15{{D}_{{{\text{eff}}}}}}}\frac{{d\overline {{{q}_{t}}} }}{{dt}}.$$
((13))

To obtain an equation only in C, we use the mass balance equation (Eq. (6)) to rewrite \(~\frac{{d\overline {{{q}_{t}}} }}{{dt}}\) in terms of C (Eq. (14), and then substitute it in Eq. (13) as follows:

$$V\frac{{dC}}{{dt}} = ~ - {{V}_{p}}\frac{{d\overline {{{q}_{t}}} }}{{dt}} \to \;\frac{{d\overline {{{q}_{t}}} }}{{dt}} = - \frac{{\text{V}}}{{{{V}_{p}}}}\frac{{dC}}{{dt}},$$
((14))
$$\overline {{{q}_{t}}} = \frac{{{{q}_{m}}{{K}_{L}}\left( {C + \frac{R}{{3{{K}_{f}}}}\frac{{\text{V}}}{{{{V}_{p}}}}\frac{{dC}}{{dt}}} \right)}}{{1 + {{K}_{L}}\left( {C + \frac{R}{{3{{K}_{f}}}}\frac{{\text{V}}}{{{{V}_{p}}}}\frac{{dC}}{{dt}}} \right)}} + \frac{{{{R}^{2}}}}{{15{{D}_{{{\text{eff}}}}}}}\frac{{\text{V}}}{{{{V}_{p}}}}\frac{{dC}}{{dt}}.$$
((15))

Using Eq. (6), we substitute \(\overline {{{q}_{t}}} = ~\,{{q}_{0}} - \frac{V}{{{{V}_{p}}}}\left( {C - {{C}_{0}}} \right)\) in Eq. (15) to obtain an equation in terms of only C:

$$\begin{gathered} \left( {{{q}_{0}} + \frac{V}{{{{V}_{p}}}}{{C}_{0}}} \right) - \frac{V}{{{{V}_{p}}}}C \\ = \,\,\frac{{{{q}_{m}}{{K}_{L}}\left( {C + \beta \frac{{dC}}{{dt}}} \right)}}{{1 + {{K}_{L}}\left( {C + \beta \frac{{dC}}{{dt}}} \right)}} + \alpha \frac{{\text{V}}}{{{{V}_{p}}}}\frac{{dC}}{{dt}}, \\ \end{gathered} $$
((16))

which can be arranged in the following form:

$$\begin{gathered} \left( {\gamma - \frac{V}{{{{V}_{p}}}}\left( {C + \alpha \frac{{dC}}{{dt}}} \right)} \right)\left( {1 + {{K}_{L}}\left( {C + \beta \frac{{dC}}{{dt}}} \right)} \right) \\ - \,\,{{q}_{m}}{{K}_{L}}\left( {C + \beta \frac{{dC}}{{dt}}} \right) = 0, \\ \alpha = \frac{{{{R}^{2}}}}{{15{{D}_{{{\text{eff}}}}}}}~,\,\,\beta = ~\frac{R}{{3{{K}_{f}}}}\frac{{\text{V}}}{{{{V}_{p}}}}\;,\,\,\gamma = {{q}_{0}} + \frac{V}{{{{V}_{p}}}}{{C}_{0}}. \\ \end{gathered} $$
((17))

The mathematical model Eq. (17) is an initial value problem which is solved using the finite difference method and COMSOL Multiphysics code to estimate C during process time. Then, the variations of \(\overline {{{q}_{t}}} \) during time are resolved from Eq. (6). Kinetic studies were carried out by contacting 0.02 g of the adsorbent to 50 mL of 10, 50 and 90 mg/L lead solutions with the same pH 6 and under mixture agitating at 100 rpm. The isotherm experiments were conducted for 50mg/L lead solution at the constant temperatures 20, 40 and 60°C for 2 hours to ensure the adsorption equilibrium. The aqueous samples were taken for the lead concentration measurements using a Buck 210 atomic absorption spectrophotometer.

RESULTS AND DISCUSSION

The experimental data of the lead adsorption onto the adsorbent (clinoptilolite/magnetite/chitosan) were analyzed using the pseudo-second-order kinetics model (Fig. 2), the intraparticle diffusion mechanism model (Fig. 3), and the Langmuir isotherm model (Fig. 4). The correlation coefficient R2 was used to express the uniformity between the experimental data and the model-predicted values.

Fig. 2.
figure 2

Lead concentration in the absorbent particle with different initial lead concentrations (the experimental data (a) and the second-order kinetics predictions (b), 0.02 g adsorbent, 20°C and pH 6).

Full size image
Fig. 3.
figure 3

The plots of lead concentration in the absorbent particle vs. t0.5 with different initial lead concentrations (0.02 g adsorbent, 20°C and pH 6).

Full size image
Fig. 4.
figure 4

Lead adsorption isotherm at different temperatures (the experimental data and the Langmuir predictions, 0.02 g adsorbent, 50 mg/L initial lead concentration and pH 6).

Full size image

The pseudo-second-order model in linearized form can be written as

$$\frac{t}{{{{q}_{t}}}} = \frac{1}{{{{k}_{2}}{{q}_{e}}^{2}}} + \frac{t}{{{{q}_{e}}}}~,$$
((18))

where k2 is the rate constant. This model contains external film diffusion, intraparticle diffusion and interaction step between metal ions and the functional groups of the adsorbent during the adsorption process. The results illustrate that the adsorption kinetics follows the pseudo-second-order kinetic model due to its correlation coefficient (Table 2), which suggests that the lead adsorption process is very fast [24].

Table 2.   Second-order kinetics parameters for different initial lead concentrations
Full size table

The intraparticle diffusion mechanism model describes the transfer of adsorbate from the solution bulk to the adsorbent phase. This model can be expressed as

$${{q}_{t}} = {{K}_{{{\text{intra}}}}}{{t}^{{0.5}}} + {{C}_{1}},$$
((19))

where Kintra is the intraparticle diffusion rate constant and C1 is the intraparticle diffusion rate constant related to the boundary layer thickness. For the adsorption process controlled by the intraparticle diffusion, the plots of qt versus t0.5 give straight lines, while the data may exhibit multilinear plots. The plots of qt versus t0.5 and the calculated parameters are shown in Fig. 3 and Table 3, respectively. The results suggest that more than one stage influence the adsorption process and the order of Ki,1> Ki,2> Ki,3 can be attributed to the adsorption stages of the exterior surface, interior surface and the equilibrium, respectively.

Table 3.   Intraparticle diffusion mechanism model parameters for different initial lead concentrations
Full size table

The Langmuir model has been successfully applied for many monolayer adsorption processes. It can be represented as follows

$$\frac{{{{C}_{e}}}}{{{{q}_{e}}}} = \frac{{{{C}_{e}}}}{{{{q}_{m}}}} + \frac{1}{{{{q}_{m}}{{K}_{L}}}},$$
((20))

where qm and KL are the maximum capacity of the adsorbent and the Langmuir adsorption constant, respectively. The dimensionless equilibrium parameter RL has been determined to predict the type of the adsorption process which can be written as

$${{R}_{L}} = \frac{1}{{1 + {{K}_{L}}{{C}_{0}}}},$$
((21))

where C0 is the initial lead concentration and RL indicates the type of isotherm to be either linear or irreversible when RL is 1 or 0 correspondingly, while the isotherm type is favorable for 0 < RL < 1 or unfavorable for RL > 1. The constants of Langmuir isotherm for the adsorption of lead are summarized in Table 4, in which it can be concluded from R2 values that Langmuir model very well fits the experimental data. Also, the values of RL ranging from 0.005 to 0.13 indicate the favorable adsorption between the adsorbent and lead [11].

Table 4.   Langmuir isotherm constants for different temperatures
Full size table

The maximum capacity of the adsorbent is 136.99 mg/g indicating a large adsorption capacity for the lead. Table 5 indicates the comparison of lead adsorption capacity of the adsorbent with various adsorbents reported in the literature [25–28].

Table 5.   Comparison of adsorption capacity of various adsorbents for lead ions
Full size table

A good agreement between the numerical results and the experimental kinetic profiles was found. The concentration decays data and qt profiles (C and \(\overline {{{q}_{t}}} \) vs. time) for different initial lead concentration in solution, have been used to determine the unknown process parameter, Deff, using the above numerical procedure as some of theme shown in Figs. 5 and 6. These values of Deff are used to simulate the adsorption kinetics for different operating conditions.

Fig. 5.
figure 5

Solution lead concentration decay with different initial lead concentrations of 7.5, 35, and 65 mg/L in the solution (comparison of experimental data versus model predictions).

Full size image
Fig. 6.
figure 6

Lead concentration profile in the absorbent particle with different initial lead concentrations of 7.5, 35, and 65 mg/L in the solution (comparison of experimental data versus model predictions).

Full size image

Parametric Study

The effect of different parameters influencing the adsorption kinetics such as the particle size of the adsorbent, the volume of the lead solution, the volume of the adsorbent and the initial lead concentration in the liquid was studied. The model predictions seem to be reasonable. As can be seen from Fig. 7, the rate of the adsorption increases with the decrease of the particle size of the adsorbent . This is due to the fact that the total surface area of smaller particles, and consequently, the number of adsorption sites, is larger than that of larger particles for the same amount of the mass of the adsorbent [17]. Since the mass of the adsorbent is the same, the final stationary concentration is the same for all different particle sizes.

Fig. 7.
figure 7

Effect of the adsorbent particle size on lead adsorption (0.02 g adsorbent, 50 mL solution, 50 mg/L initial lead concentration).

Full size image

As the adsorbent volume increases, the number of adsorbent sites available for the lead ions increases and consequently, a better adsorption takes place and the rate of adsorption increases [29]. This leads to a lower lead concentration in the solution, as illustrated in Fig. 8.

Fig. 8.
figure 8

Effect of the adsorbent volume on lead adsorption (50 mg/L initial lead concentration, 3 µm adsorbent radius, 50 mL solution).

Full size image

As shown in Fig. 9, with a decrease in the initial lead concentration in the solution, the rate of the adsorption increases. When the lead concentration is high, the lead ions could bind to the abundant adsorption sites on the surface of the adsorbent and the adsorbent adsorptivity increased. Thus, the higher the initial lead ion concentrations, the slower the adsorption rate due to occupying many of the adsorption sites [30].

Fig. 9.
figure 9

Effect of the initial lead concentration on lead adsorption (0.02 g adsorbent, 50 mL solution, 3 µm adsorbent radius).

Full size image

Figure 10 presents the effect of the volume of the lead solution on the lead adsorption. With an increase in the volume of the lead solution, the adsorption rate decreases. For a given initial lead concentration and the mass of the adsorbent, this can be explained so as the volume of the lead solution decreases, the solution adsorbent dose increases. Therefore, a larger surface area of the absorbent is available which exposes more adsorption sites for the lead ions [31].

Fig. 10.
figure 10

Effect of the volume of the lead solution on the adsorption of lead (0.02 g adsorbent, 50 mg/L initial lead concentration, 3 µm adsorbent radius).

Full size image

CONCLUSIONS

The natural zeolite (clinoptilolite) was magnetized by the precipitation of magnetite on it with FeCl2 ⋅ 4H2O and FeCl3 ⋅ 6H2O solutions, then was functionalized with chitosan by the glutaraldehyde crosslinker and the final composite was used for the lead removal from a batch adsorption system. The experimental data of the lead adsorption onto the adsorbent were analyzed using the pseudo-second order kinetics model and the Langmuir isotherm model. These models well fit the experimental kinetics and isotherm data. A two-resistance model based on the external mass transfer and the homogeneous solid diffusion has been studied in the present work. The model has successfully been applied using the finite difference method to simulate a batch adsorption system and to fit the experimental data for different initial lead concentrations. A good agreement between the numerical and the experimental results for the lead concentration in liquid and solid phases was found. A parametric study has been carried out to study the effects of the particle size of the adsorbent, the initial adsorbate concentration, the solution volume and the amount of the adsorbent on the adsorption kinetics. It was found that the lead adsorption rate increased with a decrease in each of the initial lead concentration, the particle size of adsorbent and the volume of the adsorbate solution. On the other hand, an increase in the volume of the adsorbent increases the lead adsorption rate. The results showed that the adsorption kinetics follows the pseudo-second-order kinetic model due to its correlation coefficients (R2), suggesting that the lead adsorption process is very fast. Also, an adsorbent maximum capacity of 136.99 mg/g was found, indicating a large adsorption capacity for lead.