INTRODUCTION

The fact that there is a correlation between ultimate tensile strength σu and Brinell hardness for some groups of steels is known for a long time. Such correlations enable quick estimation of σu from the data on HB without fabricating specimens. Therefore, numerous research were performed to establish a more general correlation of σu with HB for steels of various classes and grades, and such investigations have been performed up to now. As a result of these studies, formulas, plots, and tables were proposed for determination of σu from HB for specific steel classes. The results are described, for example, in [1–4] and also in normative documents (e.g., GOST 22761, RTM3-1947–91, and Instruction I 1.2.102.019.1121–2016).

The σu–HB correlations are most often approximated by the following linear dependences:

$${{\sigma }_{{\text{u}}}} = c \cdot HB \pm b,$$

where c and b are constant coefficients characteristic of specific groups of materials.

If coefficient b is very small, it can be neglected in practice.

For nonferrous metals and alloys based on them, the data on the correlation between σu and HB are scarce as compared to steels. However, RTM3-1947–91 contains tables, which give the values of σu and HB for some nonferrous alloys based on aluminum, copper, and titanium.

However, it should be noted that, even for steels, the estimation of σu using the date on HB and known relationships is approximate and can be used for specific groups of steels with known compositions and strength and the hardness. Coefficients c and b in Eq. (1) can be substantially varied as functions of treatment conditions and the microstructure of steels.

Therefore, attempts to propose more justified and general σu–HB correlations taking into account the strain-hardening parameters of materials were made in the mid-20th century. In [5, 6], such a parameter was the strain-hardening coefficient n entering in the Meyer formula

$$F = a \cdot {{d}^{n}},$$
(2)

where F is the indentation load of a ball indenter, d is the indentation diameter, a is the coefficient characteristic of a material and depending on indenter diameter D, and n is the strain-hardening coefficient.

In [7, 8], such a parameter was taken to be the limiting uniform elongation of a specimen during tension δu. Markovets [7] was the first to formulate one of the main similarity conditions: the tensile stress of a specimen should be placed in correspondence with its Brinell hardness at the same plastic strain during tension and indentation. Markovets proposed to estimate the conventional plastic strain during indentation using the following relationship:

$${{\Psi }^{{{\text{ind}}}}} = \frac{1}{2}\left[ {1 - \sqrt {1 - {{{\left( {\frac{d}{D}} \right)}}^{2}}} } \right].$$

Based on this similarity condition, to estimate σu using the data on HB, it is necessary to provide, during a ball indentation, the plastic deformation in the indentation \(\Psi _{{\text{u}}}^{{{\text{ind}}}}\) that is equal to the residual ultimate uniform tensile strain of the specimen corresponding to σu. The correlation between σu and HBmax should be established with allowance for the existence of a maximum in the stress σ–relative elongation δ tensile diagram with coordinates σu and δu and also a maximum at the HB–Ψind indentation diagram with HBmax–\(\Psi _{{\text{u}}}^{{{\text{ind}}}}\) coordinates.

HBmax can be most correctly determined from HB–Ψind or HB–F indentation diagrams. However, the construction of such diagrams with determination of load F, indentation diameter d, and calculation of HB at each loading stage is a very difficult process. Therefore, formulas were proposed for calculations of HBmax from parameters a and n entering in Meyer formula (2). The most known formula is [9]

$$H{{B}^{{\max }}} = \left( {\frac{2}{\pi }} \right)a{{D}^{{n - 2}}}{{n}^{{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0em} 2}}}}{{(n - 2)}^{{(n - {2 \mathord{\left/ {\vphantom {2 2}} \right. \kern-0em} 2})}}}(n - 1).$$

Parameters a and n can be determined by two indentations of an indenter at two different arbitrary loads F1 and F2, measuring indentation diameters d1 and d2 corresponding to these loads,

$$n = (\ln {{({{{{F}_{2}}} \mathord{\left/ {\vphantom {{{{F}_{2}}} {{{F}_{1}})}}} \right. \kern-0em} {{{F}_{1}})}}} \mathord{\left/ {\vphantom {{({{{{F}_{2}}} \mathord{\left/ {\vphantom {{{{F}_{2}}} {{{F}_{1}})}}} \right. \kern-0em} {{{F}_{1}})}}} {\ln ({{{{d}_{2}}} \mathord{\left/ {\vphantom {{{{d}_{2}}} {{{d}_{1}})).}}} \right. \kern-0em} {{{d}_{1}})).}}}}} \right. \kern-0em} {\ln ({{{{d}_{2}}} \mathord{\left/ {\vphantom {{{{d}_{2}}} {{{d}_{1}})).}}} \right. \kern-0em} {{{d}_{1}})).}}}}$$

However, the accuracy of determining parameter n is significantly dependent on the chosen ratio of loads F2/F1, which can be different in the dependence on the mechanical properties of a material. Ratio F2/F1 can be justifiably determined only using an indentation diagram.

Therefore, in 1968, researchers of MPEI under direction of Prof. M.P. Markovets proposed to determine HBmax using depth-sensing (instrumented) indentation [1]. This method was developed and gained recognition due to more perfect instruments and information measurement engineering, and now it is possible to quickly and reliably determine the maximum hardness by instrumented indentation recording a ball indentation diagram in the load–indentation depth coordinates [10]. In this work, we perform comprehensive experimental studies, including the determination of the maximum Brinell hardness by instrumented indentation for materials of various classes and grades. The aim of this work is to establish a general correlation between the ultimate strength with the maximum Brinell hardness of ferrous and nonferrous metal and alloys.

EXPERIMENTAL

We prepared specimens for tensile tests and indentation tests from various steels and alloys based on nonferrous metals. The steels to be studied were carbon steels and also alloy steels of pearlitic, austenitic, ferritic–martensitic and martensitic classes with σu from 300 to 1700 N/mm2 (in all, 18 types of steels). The group of nonferrous alloys consisted of alloys based on aluminum (18 alloys), magnesium (3 alloys), and titanium (9 alloys). The aluminum alloys had σu from 100 to 700 N/mm2, magnesium alloys, from 240 to 280 N/mm2, and titanium alloys, from 380 to 1216 N/mm2.

To determine the ultimate strength by tensile tests according to GOST 1497–84 as a function of the range of sizes, either cylindrical tensile specimens (type III) or proportional planar specimens with heads (type I) were prepared from each material under study. Tensile tests were carried out on an Instron 5982 universal testing machine at a strain rate of 2 mm/min (3.3 × 10–4 m/s). Three specimens were tested per material, and the resulting ultimate strength σu was calculated as the value averaged over the results of three tests.

The hardness characteristics of a material were determined by several various methods.

At the first stage, the Brinell hardness was measured on each of the materials according to GOST 9012. Tests were carried out on a MEI-T7 device using an indenter of diameter D = 2.5 mm. The indentation load FG was 1839 N (187.5 kg) for materials with hardness HB > 100 kg/mm2 and 307 N (31.25 kg) for materials with a lower hardness. The resulting values of Brinell hardness HB were found as the average of three measurements.

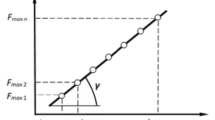
Then, on each of the materials, tests were carried out by stepwise loading of an indenter with a step-by-step increase in indentation load F and the measurement of indentation diameter d at each step of loading. These tests were also performed on the MEI-T7 device using an indenter of diameter D = 2.5 mm. The results of these tests were used to build stepwise HB–F indentation diagrams with the determination of the hardness at each loading step. Such diagrams enabled us to determine maximum hardness HB  max, load F  max, and the degree of loading K  max = F  max/D2 at which this hardness is attained.

Instrumented indentation tests were carried out on the Instron 5982 testing machine, recording a load–indenter displacement indentation diagram. The indentation loads were chosen to assure the achievement of the maximum hardness for each of the materials taking into account the results obtained during the step-by-step loading of the indenter. Then, these diagrams were converted into unrecovered Brinell hardness HBt–relative indentation depth t/R diagrams using the algorithms and programs developed in [10]. These HBt–t/R diagrams were used to determine the maximum hardness \(HB_{t}^{{\max }}\). Three indentation diagrams were recorded for each of the materials, and the resulting values of the Brinell hardness HB were found as the average of three measurements.

After the tensile and indentation tests, the obtained results were compared. The values of ultimate strength found by the tensile methods were put in correspondence with the Brinell hardness determined according to GOST 9012 (σu/HB  ), the maximum hardness determined by step-by-step loading (σu/HBmax), and the maximum hardness determined by instrumented indentation (σu/\(HB_{t}^{{\max }}\)).

RESULTS AND DISCUSSION

To compare the ultimate tensile strength and the Brinell hardness HB determined according to GOST 9012, we built the dependences of σu on HB for steels (Fig. 1a), aluminum and magnesium alloys (Fig. 1b), and titanium alloys (Fig. 1c). When constructing the general σu(HB) dependence for all abovementioned materials, we observed a substantial scatter of the experimental points and, hence, divided the materials into groups. After statistical processing of the curves presented in Fig. 1, the following formulas were obtained, where the values of σu and HB are given in N/mm2 (correlation coefficient r is indicated in parentheses):

Fig. 1.
figure 1

Ultimate tensile strength σu vs. Brinell hardness HB for (a) steels, (b) aluminum and magnesium alloys, and (c) titanium alloys.

Full size image

for steels, σu = 0.369HB – 59.5 (r = 0.995);

for aluminum and magnesium alloys, σu = 0.378HB + 13.4 (r = 0.952);

for titanium alloys, σu = 0.337HB + 8.1 (r = 0.986).

The lowest correlation coefficient r was obtained for aluminum and magnesium alloys. The difference of the values of σu calculated by the obtained formulas and the values of σu obtained by the tensile tests of the specimens is ±25% for aluminum and magnesium alloys, ±12.5% for titanium alloys, and ±11% for steels.

When comparing σu with hardness HB determined under the loads recommended by GOST 9012, it is impossible to obtain a quite correct general correlation for various ferrous and nonferrous metals and alloys. The cause is that the indentation load Fmax at which the maximum hardness is reached can be substantially different from load FG recommended by GOST 9012 for the determination of the Brinell hardness for some materials. In this case, the tensile maximum stress σu is actually compared not to the maximum hardness; correspondingly, the relation between these stresses can vary within over limits as a function of a material. This fact supports the assumption that it is necessary to relate σu to the maximum Brinell hardness HBmax to obtain justified general relations between σu and the hardness.

Figure 2 shows the obtained stepwise indentation diagrams for some steels, aluminum, magnesium, and titanium alloys. It is seen from the diagrams that load F  max at which maximum hardness HB max is achieved is most often higher than load FG regulated by GOST 9012. For some materials, F  max is equal or very close to F G. However, for an AMts aluminum alloy, which has a small uniform deformation during tension of a specimen, load F  max was significantly lower than F G. Expressing the indentation load as the degree of loading K = F/D2, we can see that, in most cases, the degree of loading K  max = F  max/D2 at which the maximum hardness is achieved is significantly higher than the degree of loading K  G = F G/D2 regulated by GOST 9012. The highest value K  max = 675 N/mm2 was obtained for EP184 austenitic steel, and the lowest value K  max = 31.4 N/mm2, for an AMts aluminum alloy.

Fig. 2.
figure 2

Step-by-step HB–F indentation diagram for structural materials (D = 2.5 mm): (1) MA20, (2) AMg6, (3) VT1-0, (4) EP184, and (5) V95T1.

Full size image

Table 1 gives the values of F  G, F  max, K  G, K  max, HB, and HB  max for several grades of steels, aluminum and magnesium alloys, and titanium alloys. The ratios σu/HB  max determined for all materials presented in Table 1 are close to 1/3. Here, it should be noted that the ratio σu/HB, in which hardness HB is determined by GOST 9012, has values from 0.336 to 0.508. For titanium alloys, the values of σu/HB and σu/HBmax differ insignificantly, since the indentation load is F G ≈ F  max.

Table 1.   Results of determining the mechanical properties of steels and alloys based on nonferrous metals
Full size table

When instrumented indentation is used upon recording a load F–indenter displacement α indentation diagram and subsequent conversion of this diagram into an HBt–t/R diagram, the process of testing and determination of (HBt)max is accelerated and takes no longer than 3 min. The regularities and properties of such diagrams are considered in [11]. Figure 3 shows F–α and HBt–t/R indentation diagrams for several materials tested in this work.

Fig. 3.
figure 3

(a) F–α and HBt–t/R indentation diagrams for structural materials (D = 2.5 mm) obtained by instrumented indentation: (1) MA20, (2) AMg6, (3) VT1-0, (4) EP184, and (5) V95T1.

Full size image

Table 1 also gives the values of \(HB_{t}^{{\max }}\) and ratios σu/(HBt)max. From Table 1, it is seen that the values of σu/(HBt)max are close to 1/3 for all materials under study.

The statistical processing of σu–(HB)max and σu–(HBt)max for all the materials subjected to the tests resulted in the following formulas (correlation coefficient r is indicated in parentheses), in which the values of σu and HB are given in N/mm2:

$${{\sigma }_{{\text{u}}}} = 0.336H{{B}^{{\max }}} - 2.7\,\,\,(r = 0.999),$$
(3)
$${{\sigma }_{{\text{u}}}} = 0.322{{(H{{B}_{t}})}^{{\max }}} - 3.0\,\,\,(r = 0.998).$$
(4)

An experimental verification showed that the maximum difference in the values of σu determined by indentation and calculated using Eqs. (3), (4) and the values of σu found in tensile tests is at most ±5%.

Formulas (3) and (4) are valid when a indenter with D = 2.5 mm is used. It is interesting to note that the relation of σu to HB was found earlier without considering the influence of the scale factor. We used the values of the hardness determined by indentation of various indenters of diameters D = 10–1 mm. However, the smaller D, the higher hardness HB. By analogy, in the case of tensile tests, σu increases when the initial cross-sectional area decreases [12].

Completing the consideration of the σu–HB relations, we should note that the relations of σu to the Vickers hardness HV are also known for specific groups of materials. For example, the relations between σu and HV for several grades of steels presented in [13] are also described by a linear dependence, which is similar to Eq. (1). However, a general σu–HV relation for ferrous and nonferrous metals cannot be established for the following reason. It is known that the indentation of a Vickers pyramid with a apex angle of 136° leads to a conventional contact deformation of approximately 0.073 [10]. This deformation remains constant on the macroscale of indentation at various indentation loads and pyramid indentation depths. When a ball is indented, the same deformation is achieved at a relative indentation diameter d/D = 0.376, which corresponds to the indentation angle of 136°. Under this condition for materials with a limiting uniform tensile deformation close to 0.073, general directly proportional relations σu–HB and σu–HV take place with a coefficient of proportionality close to 1/3. When the limiting uniform deformation of the material is higher or lower than 0.073, the σu–HB and σu–HV relations are described by Eq. (1) with various coefficients. Therefore, instrumented pyramid indentation with recording a load–indenter displacement indentation diagram cannot be used to find a general relation between σu and HV for ferrous and nonferrous metals.

CONCLUSIONS

The experiments on ball indentation performed in this work to determine (HB)max and (HBt)max using indentation diagrams and to determine σu from tensile diagrams of various steels, aluminum, magnesium, and titanium alloys showed that there is general direct proportional relation between these mechanical characteristics. The maximum deviation of the values of σu found by the revealed relation from the values of σu found from tensile tests of specimens is at most ±5% for all materials.

When σu was compared to HB under the loads recommended by GOST 9012, it is impossible to obtain a fairly correct general relation for various ferrous and nonferrous metals and alloys. The main cause of this fact is that indentation the load (F  max) at which the maximum hardness is achieved can significantly differ from the load (FG) recommended by GOST 9012 to determine the Brinell hardness for some materials. It was found that a justified general correlation between σu and the hardness can only be obtained when σu is compared to the maximum Brinell hardness HBmax determined from an indentation diagram. In addition, in the search for a correlation between σu and the hardness, the conditions of the physical, mechanical, and geometric similarities should be met and tensile and indentation tests should be carried out on the same scale.