Collision-Induced Transformation of the Complex Vibrational Susceptibility of a Linear Molecule Using the Example of the ν₃ Band of Carbon Dioxide

Abstract

The simultaneous transformation of both components of the complex isotropic vibrational susceptibility, which occurs with an increase in the density of a gas consisting of linear molecules, is traced for the first time in terms of the quantum model of strong collisions. The vibrational susceptibility of the CO₂ molecule in the region of the fundamental ν₃ band is discussed in detail as a case in point. It is found that within the region of anomalous dispersion adjacent to frequency ν₃, there is a spectral interval that is characterized by positive dispersion and exists in a fairly wide pressure range. This interval narrows upon an increase in pressure and disappears at a density of around 100 Amagat, completely blurring the branch structure of the absorption band. It is shown that allowing for the spectral exchange between the lines of the rotational structure of the band is equally important for quantitatively interpreting the spectrum of the real part of susceptibility and reproducing a correct picture of the transformation of the absorption spectrum.

INTRODUCTION

It is known that collisions broaden the lines of the rotational structure of vibrational bands [1] and produce the so-called line mixing (LM) effect [2, 3] associated with the collision-induced transfer of intensity from one line to another. The first theoretical study in this area was reported by Alekseev and Sobelman [4], who showed that LM can radically alter the contours of isotropic Raman bands and reduce their half-widths at high pressures. This study stimulated a great many others that are currently based on the concept of a rotational relaxation Γ matrix, the off-diagonal part of which is responsible for LM. Many studies (see, e.g., [3]) have focused on calculating and modeling this matrix for different spectroscopic means (infrared (IR) absorption, Raman spectroscopy, nonlinear optics). In addition to solving purely academic problems of the dynamics of compressed gases, studies of the rotational Γ matrix are of great importance in, e.g., interpreting satellite measurements of the spectra of the Earth’s atmosphere and those of other planets, and the optical sounding of gases in the combustion chambers and nozzles of jet engines.

Raman spectra, the contours of which are formed by the dynamics of quadratic fluctuations of molecular polarizability in a real gas, are not discussed below. Only IR responses determined by the dynamics of the vibrational dipole moment are analyzed. The standard approach in this case is to study the effect collisions have on the contours of the vibrational bands of IR absorption, which is determined by the imaginary part of linear vibrational susceptibility $A_{\nu }^{{''}}$(ω). To the best of our knowledge, the accompanying transformation of the real part of susceptibility ($A_{\nu }^{'}$(ω)) remains poorly understood, and it is this process on which we focus in this work. Note that calculating $A_{\nu }^{'}$(ω) with a known Γ matrix is not difficult and allows us to avoid Kramers–Kronig transforms that relate the two parts of ${{A}_{\nu }}$(ω).

Modeling $A_{\nu }^{'}$(ω) allows determination of the resonant part of refractive index n(ω), a fundamental characteristic that must be known in order to calculate coherent nonlinear optical responses, processes of radiation transfer, and characteristics of the resonant reemission of photons by matter.

FOUNDATIONS OF THE THEORETICAL APPROACH

The purely vibrational contribution ${{n}_{\nu }}$(ω) to n(ω) near the dipole-allowed vibrational transition in a moderate-density gas is discussed below. The rotational and electronic terms of n(ω) in this region are proportional to number d of molecules per unit volume and have a weak dispersion that does not depend on the density of the gas. Using the linear relationship of ${{A}_{\nu }}$(ω) with the isotropic part of the vibrational molecular polarizability ${{\alpha }_{\nu }}(\omega )~$, we arrive at the simple equation [5]

$${{n}_{\nu }}(\omega ) = 1 + 2\pi d\alpha _{\nu }^{'}(\omega ),$$

(1)

in which ${{\alpha }_{\nu }}(\omega )~$ exhibits a fairly complex dependence on d due to rotational relaxation. The quantum Liouville formalism gives us the expression¹

$$\begin{gathered} {{{{\alpha }}}_{\nu }}({{\omega }}) = \frac{{m_{\nu }^{2}}}{3}~\operatorname{Tr} X{{[{{L}_{0}} - \Delta \omega - i\Gamma ]}^{{ - 1}}}X \\ = \frac{{m_{\nu }^{2}}}{3}\mathop \sum \limits_{KK'} {{X}_{K}}{{X}_{{K'}}}[{{L}_{0}} - \Delta \omega - i\Gamma ]_{{KK'}}^{{ - 1}}~{\kern 1pt} , \\ \end{gathered} $$

(2)

where indices $K{{\;}}$ and $~K{\kern 1pt} '$ denote the (i, f) and (i', f ') pairs of states responsible for allowed rotational transitions within the band, and Δω is the deviation from the frequency of the vibrational transition ${{\omega }_{v}}$. In this equation, ${{X}_{K}} = \sqrt {{{\rho }_{{ii}}}} {{m}_{{if}}}$, where ρ_ii is the rotational Boltzmann factor and m_if denotes the reduced rotational matrix element of the dipole moment. The eigenvalues of rotational Liouvillian L₀ are frequencies ${{\omega }_{K}}$ of allowed rotational transitions, and $m_{v}^{2}$ is the square of the vibrational matrix element. Difficulties in using (2) are associated with both the infinite dimension of the Г matrix and the lack of comprehensive data on the most important matrix elements for most molecules. To overcome these obstacles, we must postulate the form of this matrix, allowing for the general properties of the matrix and for the character of collisions. One of the most commonly used models of Г is the strong collision (SC) model developed for both classical [1] and quantum rotators [6–10]. The model assumes complete thermalization of the probability of states after a collision at any energy of the initial state. This makes the SC model realistic for slow rotators, the states of which are readily disrupted by the impact of buffer particles. This model was successfully tested in [8, 11–13] for modeling the envelopes of the vibrational bands of CO₂ of different origins.

An attractive feature of the SC model is the possibility of analytically inverting the spectral matrix in Eqs. (2). It is noteworthy that with quanta, the result is even simpler than in the classical case [1]. In the original formulation (SC1) [6–9], the quantum Г_SC matrix was expressed in terms of matrices projected onto vector X of the Liouville space, the basis of which is composed of operators of allowed optical transitions, and contained a single parameter—γ—denoting the average half-width of the rotational components. Note too that using SC1 reproduces the result for the spectral function obtained in [10] from heuristic considerations.

It is obvious that the single-parameter SC1 model does not accurately reproduce the spectrum at low pressures. In actual practice, half-widths γ_K always depend on the combining states. The improved SC2 model [7] contains this dependence. If it is taken from experimental data, SC2 will ideally reproduce the experimental absorption spectrum at low pressures. It was shown in [7] that like SC1, SC2 provides a simple analytical expression of the spectrum and predicts the collapse of the absorption band structure due to the effect of line interference upon a rise in pressure. After introducing the static value of vibrational polarizability ${{\alpha }_{\nu }} = 2m_{\nu }^{2}{\text{/}}3\hbar {{\omega }_{\nu }}$, the SC2 result [7] can be written in the dimensionless form

$$\begin{gathered} \sigma (\omega ) \equiv \frac{{2{{\alpha }_{\nu }}(\omega )}}{{{{\alpha }_{\nu }}}} = {{\omega }_{\nu }}\{ {{S}_{0}}(\Delta \omega ) \\ + \;S_{1}^{2}(\Delta \omega ){\text{/}}[\gamma - i{{S}_{2}}(\Delta \omega )]\} , \\ \end{gathered} $$

(3)

where the S_n (n = 0, 1, 2) spectral functions are defined as

$${{S}_{n}}(\Delta \omega ) = \mathop \sum \limits_K \frac{{X_{K}^{2}\gamma _{K}^{n}}}{{{{\omega }_{K}} - \Delta \omega - i{{\gamma }_{K}}}}.$$

(4)

It is easy to interpret the result (3). The first term in curly brackets corresponds to noninteracting lines. The second term is associated with the LM effect and is negligible at low pressures (low rates of relaxation). However, it grows along with the density of the gas and compensates the role of the first term, resulting to spectral collapse and the narrowing of the shape of the imaginary part of susceptibility.

RESULTS AND DISCUSSION

The object of our calculations was the ${{\nu }_{3}}$ band (2349 cm⁻¹)² of pure carbon dioxide as a gas of great importance for different applications. The studied range of reduced densities³d* of the gas was 2–200 Amagat, where binary collisions predominate. Value ${{m}_{\nu }} = 0.128~$ of the vibrational matrix element in atomic units (au) was taken from [14], and the spectroscopic constants were taken from [15]. In atomic units, this results in the value is ${{\alpha }_{\nu }} =$ 1.021. The dependence of self-broadening coefficients (in cm⁻¹/Amagat) on rotational quantum number J was taken in the form $\gamma (J) =$ $0.13{\text{exp}}( - 0.00726J)$, which satisfactorily approximates the set of the IR and Raman data [16]. Since this dependence is extremely weak for the most intense lines of the band, the results of SC1 and SC2 for cases of blurred spectra are virtually identical.

Definition (3) gives dimensionless factor $\sigma {\kern 1pt} '(\omega )$ for the real part of the polarizability with normalization $\sigma {\kern 1pt} '(0) = 1$. Imaginary part $\sigma {\kern 1pt} ''(\omega )$ determines the coefficient of absorption $k(\omega )$

$$k(\omega ) = 2\pi d{{\alpha }_{\nu }}\frac{{{{\omega }_{\nu }}}}{c}\kappa (\omega ),$$

(5)

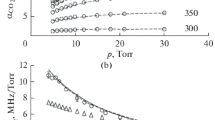
via dimensionless factor $\kappa (\omega ) \equiv {{\omega }}\sigma {\kern 1pt} {{''}}(\omega ){\text{/}}{{\omega }_{\nu }}$. Since the half-width of the band is much smaller than ${{\omega }_{\nu }}$, κ(ω) differs from $\sigma {\kern 1pt} ''(\omega )$ only slightly, and graphs of it can be plotted on the same scale as dependences $\sigma {\kern 1pt} '{\kern 1pt} (\omega )$. Figures 1–5 show dependences of the contours of $\sigma {\kern 1pt} '(\omega )$ and κ(ω) on pressure at room temperature. The plots in Fig. 1 represent both functions calculated at extreme pressures: (i) with a well-resolved rotational structure at d* = 2 Amagat and (ii) a structureless band at d* = 200 Amagat. The shape of the imaginary part of polarizability exhibits the pressure-induced narrowing effect, and the anomalous dispersion is in much greater contrast when allowing for LM. There is virtually no line interference effect at low densities. According to Fig. 1, however, ignoring this effect at growing pressure gives unrealistically diffuse curves for both parts of polarizability and underestimates $|{\kern 1pt} \alpha _{\nu }^{'}(\omega ){\kern 1pt} |$ at frequencies within the doubled half-width (±25 cm⁻¹) of the absorption band. At densities of 20–50 Amagat, the effect LM has on the $\alpha _{\nu }^{'}(\omega )$ spectrum outside the interval of ±50 cm⁻¹ gradually disappears, but a subsequent rise in density expands this interval (see Fig. 2).

Fig. 1.

Results from calculating (curves 2–4) real part $\sigma {\kern 1pt} '$ and (curves 1, 5, 6) imaginary part κ of polarizability (see text) at low (2 Amagat; curves 1, 2) and high CO₂ densities (200 Amagat; curves 3–6) with allowance for LM (solid lines) and ignoring LM (dotted curves).

Fig. 2.

Transformation of dispersion curves $\sigma {\kern 1pt} '{\kern 1pt} (\omega )~$ upon a rise in the density of gas: (1, 2) 10, (3, 4) 20, and (5, 6) 50 Amagat. Solid lines were calculated with allowance for LM; dotted curves were calculated ignoring LM.

Fig. 3.

Effect of allowing for LM on the curves of reduced absorption coefficient κ(ω), calculated at densities of 10, 20, and 50 Amagat; the notations on the curves are the same as those in Fig. 2.

Fig. 4.

Components of the complex polarizability of CO₂, calculated in terms of the SC model at high pressures. Solid curves (1–3) show reduced coefficient of absorption κ; dotted curves (4–6) show $\sigma '$. Densities are (1, 5) 50, (2, 4) 100, and (3, 6) 200 Amagat.

Fig. 5.

Components of complex polarizability, calculated in terms of the SC model for moderate CO₂ densities (1–6). Densities are (1, 4) 10, (2, 5) 20, and (3, 6) 50 Amagat.

Characteristic features of the behavior of the imaginary part as a function of pressure are well known and have been confirmed using SC models. The line interference enriches the intensity in the middle of the band at growing pressure (Fig. 3), ultimately resulting in a structureless quasi-line which is narrowed as the gas pressure rises (Fig. 4). Ignoring LM results in strong blurring of the absorption band’s shape (see Figs. 1, 3) and overestimates of the intensity of the contour wing, which conflicts with experiments. LM thus has strongly different effects on spectral distributions $\alpha _{\nu }^{'}(\omega )$ and $\alpha _{\nu }^{{''}}(\omega )$.

A quite unexpected thing was the emergence of a dip and a subsequent burst at frequencies ±8 cm⁻¹ from frequency of vibration ν₃, so that an interval with positive dispersion appeared to the left of ${{\nu }_{3}}~$ (Fig. 5).

The appearance of this pair of extremes was attributed to the doublet (P–R) structure of the absorption band. The anomalous dispersion started to fall monotonically as soon as this structure was blurred by pressure (from around 100 Amagat) (Fig. 5). It is also interesting there were no signs of these extremes in the $\alpha _{\nu }^{'}(\omega )$ spectrum with a well-resolved structure (d* = 2 Amagat, Fig. 1). However, as soon as this fine structure was blurred by pressure (at around d* = 10 Amagat, Fig. 5), the extremes became apparent and continued to exist in a fairly wide range of gas densities (Figs. 4, 5).

CONCLUSIONS

A comparative analysis of the effect the frequency of collisions on the shapes of the real and imaginary parts of complex vibrational polarizability was performed for the first time using the example of the ν3 band of carbon dioxide. It was shown that the role of the LM effect in the real part of isotropic polarizability is as important as that in describing the collision-induced transformation of the contour of the coefficient of absorption. At moderate densities (around 10–100 Amagat), a region with positive dispersion appears within the region of anomalous dispersion adjacent to the frequency of vibrations. Calculations showed that the emergence of this region can be attributed to the doublet (P–R) structure of the ν₃ band.