Crystallization Kinetics of Potassium Sulfate Produced by Stirred Crystallization

Abstract

This paper discusses the crystallization kinetics of potassium sulfate in a stirred bed crystallizer through experimental investigation. Using classical nucleation theory, the homogeneous and heterogeneous nucleation mechanisms of potassium sulfate are studied. The induction time and critical nucleation parameters, including surface tension (γ), critical nucleation radius (r*), critical nucleation free energy (ΔG*), and critical nucleation molecule number (i*), are measured under different temperatures and supersaturation ratios. Experimental results show that as temperature and supersaturation ratio increase, induction time, critical nucleation free energy, critical nucleation radius, and critical molecule number decrease while nucleation rate increases. The crystal shape remains relatively unchanged with temperature and supersaturation ratio, but the average particle size increases with increasing supersaturation and temperature. Changes in measured nucleation parameters are consistent with classical nucleation theory. In addition, the kinetic equations of crystal nucleation and growth rate in a stirred crystallization system are fitted using population balance equations, and the results show that the growth rate increases with increasing supersaturation and stirring speed. In addition, the effects of the parameters in the nucleation rate equation suggest that suspension density has the greatest impact, followed by supersaturation ratio and stirring speed.

1 INTRODUCTION

Potassium sulfate is a basic raw material for the production of various potassium salts such as potassium carbonate and potassium persulfate. In addition, potassium sulfate is also used in industry for glass, dyes, fragrances, medicine, etc. Potassium sulfate has low moisture absorption, is not easy to agglomerate, has good physical state, is easy to apply, and is a good water-soluble potassium fertilizer as well as a physiological acid fertilizer in chemistry [1]. Currently, the main method for producing potassium salts is the evaporation crystallization method [2]. However, due to the high operating temperature during the evaporation process, this method faces problems with high energy consumption, expensive equipment, and poor quality of recovered salts due to uncontrolled supersaturation. Therefore, a low-energy desalination technology which can precisely control the supersaturation is highly desirable.

Stirring crystallization has received increasing attention in the field of wastewater desalination, as it can produce products with good dispersion, uniform crystal size, and uniform morphology. Therefore, it is necessary to study the stirring crystallization kinetics. Currently, there are few reports on nucleation parameters during potassium salt crystallization. This paper measures the induction period of potassium sulfate through experiments, and obtains nucleation parameters related to supersaturation ratio and temperature based on classical nucleation theory. By analyzing nucleation mechanisms and controlling nucleation ways, the influencing factors of crystal nucleation and growth kinetics are studied, the crystallization process is optimized, and theoretical guidance for process control is provided.

2 EXPERIMENTAL

2.1 Materials

Shanghai Aladdin Biochemical Technology Co., Ltd., China, provided K₂SO₄ (purity ≥99.5%) and anhydrous ethanol. Aqueous solutions were prepared using deionized water. The tiny crystals of K₂SO₄ were placed inside the stirred crystallizer (STC) as crystal seed material. All chemicals were used without further purification.

2.2 Experimental Procedure

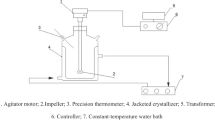
A schematic diagram of stirred crystallization is shown in Fig. 1. To begin the experiment, saturated solution is poured into the crystallizer and heated to the specified temperature. The electric stirrer is then turned on and the laser detector is activated to record the time. When a sudden change in laser intensity occurs, time recording stops as this indicates the formation of crystal nuclei. The vacuum level of the system is maintained at the set value and regulated through the adjustment valve. When supersaturation is reached, the system temperature decreases. The crystalline nuclei grow continuously in the crystallizer and sampling and filtration of the suspension are performed at regular intervals.

Fig. 1.

Experimental setup for stirred crystallization. (1) Jacketed crystallizer, (2) thermostat water bath, (3) laser transmitter, (4) laser receiver, (5) data recorder, and (6) agitator.

3 MATHEMATICAL MODELING

3.1 Population Balance Equations (PBEs)

This paper simulates the crystallization process using a Population Balance Model (PBM). The model is based on the Numerical Density Function (NDF), combined with mass and energy balance equations to describe crystallization kinetics mathematically. For intermittent crystallization, the PBM assumes that crystal growth follows the ΔL rule, and therefore, the growth rate is independent of particle size [3]:

$$\frac{{\partial n}}{{\partial t}} + \frac{{\partial (Gn)}}{{\partial L}} + \frac{Q}{V}n = \frac{{{{Q}_{i}}}}{V}{{n}_{i}} + (B - D).$$

(1)

The growth rate is represented as G, with B and D being the birth and death functions of crystals, respectively. Q represents the outflow rate of the supersaturated solution. The particle number density (n_i) is the number of crystals within the size range of ΔL_i per unit volume of suspension, which can be simplified as follows:

$${{n}_{i}} = \frac{{{{M}_{T}}{{V}_{i}}\% }}{{{{k}_{{v}}}\rho {{{({{{\bar {L}}}_{i}})}}^{3}}\Delta {{L}_{i}}}},$$

(2)

where M_T is the suspended density; V_i is the crystal volume fraction between sizes i – 1 and i; ${{k}_{{v}}}$ is the volume shape factor; L_i is the average particle size of the ith channel. The number of particles in channel ith (N_i) can be approximated as follows:

$${{N}_{i}} = {{n}_{i}}\Delta L.$$

(3)

Assuming that no slurry flows out of the crystallizer (Q = 0), and ignoring breakage and agglomeration phenomena (B = D = 0), the population balance equation (PBE) can be simplified as follows:

$$\frac{{\partial n}}{{\partial t}} + \frac{{\partial (Gn)}}{{\partial L}} = 0.$$

(4)

3.2 Nucleation and Growth

The secondary nucleation of crystals is induced by the presence of crystal seeds, and its nucleation rate can be expressed using a simple power-law model proposed by Botsaris et al. [4]:

$${{B}_{0}} = {{k}_{0}}\exp \left( { - \frac{E}{{RT}}} \right)M_{T}^{i}{{S}^{j}}N_{P}^{k},$$

(5)

$$G = {{k}_{0}}\exp \left( { - \frac{E}{{RT}}} \right){{S}^{m}}N_{P}^{n},$$

(6)

where k₀ is the pre-exponential factor; i, j, and k are nucleation orders; and m and n represent growth kinetics exponents. To simplify the PBM solution, this study introduces a transient transformation method to track crystal size distribution by solving matrices (m_j) [5]:

$${{m}_{j}} = \int\limits_0^\infty {n{{L}^{j}}dL} ,\quad j = 0,1,2,3 \ldots ,$$

(7)

when j = 0, 1, the matrices (m_j) can be calculated as follows:

$${{m}_{0}} = \int\limits_0^\infty {ndL} = N = \sum\limits_0^k {{{n}_{j}}} \Delta {{L}_{j}},$$

(8)

$${{m}_{1}} = \int\limits_0^\infty {nLdL} = {{\lambda }_{T}} = \sum\limits_0^k {{{n}_{j}}{{{\bar {L}}}_{j}}\Delta {{L}_{j}}} .$$

(9)

Taking the derivative of the left hand side of the above equation with respect to time:

$$\frac{{d{{m}_{0}}}}{{dt}} = \frac{{d\int\limits_0^\infty {ndL} }}{{dt}} = \frac{{dN}}{{dt}} = {{B}_{0}},$$

(10)

$$\frac{{d{{m}_{1}}}}{{dt}} = \frac{{d\int\limits_0^\infty {nLdL} }}{{dt}} = \frac{{d{{\lambda }_{T}}}}{{dt}} = {{m}_{0}}G.$$

(11)

When the time interval is sufficiently short, the nucleation and growth rates of crystals can be roughly considered as:

$$\frac{{d{{m}_{0}}}}{{dt}} = \frac{{\Delta {{m}_{0}}}}{{\Delta t}} = {{B}_{0}},$$

(12)

$$\frac{{d{{m}_{1}}}}{{dt}} = \frac{{\Delta {{m}_{1}}}}{{{{m}_{0}}\Delta t}} = G.$$

(13)

3.3 Nucleation Theory

The homogeneous nucleation rate based on classical nucleation theory can be expressed as:

$$J = A\exp \left( { - \frac{{\Delta G{\kern 1pt} ^*}}{{kT}}} \right).$$

(14)

Here, J is the number of nuclei that reach the critical size per unit volume per unit time, ΔG* is the free energy required to form a critical nucleus, k is the Boltzmann constant, and T is the temperature. The formation of crystalline phases leads to a change in Gibbs free energy (ΔG) [4]. Assuming that the nuclei formed by cluster aggregation are spherical, the expression for critical free energy is as follows:

$$\Delta G = 4\pi {{(r{\kern 1pt} ^*)}^{2}}\gamma + \frac{4}{3}\pi {{(r{\kern 1pt} ^*)}^{3}}\Delta {{G}_{V}},$$

(15)

where γ represents interfacial energy in J/m², and r* represents critical nucleus radius in meters. When clusters converge into a critical crystal nucleus, the critical nucleation radius can be obtained by differentiating with respect to r in Eq. (14):

$$\begin{gathered} \frac{{d(\Delta G)}}{{dr}} = 8\pi r{\kern 1pt} ^*{\kern 1pt} \gamma + 4\pi {{(r{\kern 1pt} ^*{\kern 1pt} )}^{2}}\Delta {{G}_{V}} = 0 \\ \Rightarrow r{\kern 1pt} ^* = - \frac{{2\gamma }}{{\Delta {{G}_{V}}}}. \\ \end{gathered} $$

(16)

Substituting Eq. (15) into Eq. (14). The critical free energy of the nucleus may be expressed as follows:

$$\Delta G{\kern 1pt} ^* = \frac{4}{3}\pi {{(r{\kern 1pt} ^*{\kern 1pt} )}^{2}}\gamma .$$

(17)

Equation (14) is transformed from the Gibbs-Thomson equation as follows:

$$\ln S = \ln \frac{C}{{C{\kern 1pt} ^*}} = \frac{{2\gamma {{V}_{m}}}}{{kTr{\kern 1pt} ^*}},$$

(18)

where S is the supersaturation ratio, C* is the equilibrium saturation of the solution corresponding to the operating temperature, expressed in g/mL, C is the actual concentration of the solution in g/mL, and V_m is the molar volume of the crystal expressed in m³/mol. The saturation of K₂SO₄ in water can be calculated using the following empirical formula:

$$\begin{gathered} C{\kern 1pt} ^* = 7.1431 + 9.45 \times {{10}^{{ - 2}}}T + 2.8 \times {{10}^{{ - 3}}}{{T}^{2}} \\ - \;5.0 \times {{10}^{{ - 5}}}{{T}^{3}} + 4.0 \times {{10}^{{ - 7}}}{{T}^{4}} - 1.0 \times {{10}^{{ - 9}}}{{T}^{5}}. \\ \end{gathered} $$

(19)

The Gibbs–Thomson equation $\left( {\ln S = \frac{{2\gamma Vm}}{{kTr{\kern 1pt} ^*}}} \right)$ can be utilized to derive the critical nucleus radius and free energy required for nucleation:

$$r{\kern 1pt} ^* = \frac{{2\gamma {{V}_{m}}}}{{kT\ln S}},$$

(20)

$$\Delta G{\kern 1pt} ^* = \frac{{16\pi \gamma {}^{3}V_{m}^{2}}}{{3{{k}^{2}}{{T}^{2}}{{{(\ln S)}}^{2}}}}.$$

(21)

According to classical nucleation theory, the primary nucleation rate is typically expressed as [6]:

$$J = A\exp \left( { - \frac{{16\pi {{\gamma }^{3}}V_{m}^{2}}}{{3k{}^{3}{{T}^{3}}{{{(\ln S)}}^{2}}}}} \right).$$

(22)

Induction time can be an effective research basis for evaluating crystal kinetics and inferring growth mechanisms [7, 8]:

$${{t}_{{{\text{ind}}}}} = {{t}_{r}} + {{t}_{n}} + {{t}_{g}}.$$

(23)

Induction time and nucleation rate have an inverse relationship during homogeneous nucleation [9]:

$${{t}_{{{\text{ind}}}}} \propto {{J}^{{ - 1}}}.$$

(24)

By applying logarithmic transformation, a relationship between induction period and supersaturation ratio can be derived

$$\ln {{t}_{{{\text{ind}}}}} = K + \frac{{16\pi {{\gamma }^{3}}V_{m}^{2}}}{{3{{k}^{3}}{{T}^{3}}{{{(\ln S)}}^{2}}}}.$$

(25)

A linear relationship should be observed for the plot of $\ln {{t}_{{{\text{ind}}}}}$ against $1{\text{/}}{{(\ln S)}^{2}}$ at a constant temperature with slope b:

$$b = \frac{{16\pi {{\gamma }^{3}}V_{m}^{2}}}{{3{{k}^{3}}{{t}^{3}}}}.$$

(26)

Interface free energy is a critical thermodynamic indicator, measuring the difficulty of precipitating solute crystals from a solution. The smaller the value of γ, the easier it is for crystals to form from a solution, and this can be represented by the slope b:

$$\gamma = {{\left( {\frac{{3b{{k}^{3}}{{T}^{3}}}}{{16\pi V_{m}^{2}}}} \right)}^{{1/3}}}.$$

(27)

The number of units in the critical nucleation can be represented by Eq. (28):

$$i{\kern 1pt} ^* = \frac{{4\pi {{{(r{\kern 1pt} ^*)}}^{3}}}}{{3{{V}_{m}}}}.$$

(28)

The surface entropy factor f is an important indicator for measuring the roughness of crystal surfaces. The larger the f value, the smoother the crystal surface and the more complex the crystal growth becomes. Davey believed that the surface entropy factor could be calculated using solid-liquid interfacial free energy data [10]:

$$f = \frac{{4{{V}^{{2/3}}}\gamma }}{{kT}}.$$

(29)

When the surface entropy factor of a crystal is below 3, it indicates that the crystal surface is relatively rough and can continue to grow. When greater than 5, the crystal surface is smooth and grows slowly, mainly through spiral growth or spiral dislocation growth. When the value of f is between 3 and 5, the crystal surface is relatively smooth and secondary nucleation may occur. This parameter is of great significance for further understanding the crystal growth mechanism and better controlling the polymorphism and morphology of crystals.

4 RESULT AND DISCUSSION

4.1 Primary Nucleation Kinetics

4.1.1. Crystal morphology. As shown in Figs. 2, 3, all crystal morphologies are uniform, relatively regular, and form classic rectangles with smooth surfaces and distinct edges. Changes in supersaturation ratio and temperature do not affect crystal morphology. It can be seen that with the increase of supersaturation ratio and temperature, the particle size of precipitated crystals gradually increases. The crystalline product was characterized by X-ray diffraction, and it can be seen from Fig. 4 that the system has only K₂SO₄ and is in an anhydrous state.

Fig. 2.

SEM images of K₂SO₄ crystallized from different supersaturation ratios at 328.15 K ((a) 1.20, (b) 1.22, (c) 1.25, and (d) 1.28).

Fig. 3.

SEM images of K₂SO₄ crystallized from different supersaturation at 328 K ((a) 1.20, (b) 1.22, (c) 1.25, and (d) 1.28).

Fig. 4.

The experimental XRD patterns of K₂SO₄.

4.1.2. Nucleation mechanism. From Fig. 5, it can be observed that the nucleation induction time of potassium sulfate crystal has a specific relationship with its supersaturation ratio and temperature. With the increase of supersaturation ratio and temperature, the induction time decreases nonlinearly. According to classical nucleation theory, the shorter the nucleation induction time, the higher the primary nucleation rate, indicating that both supersaturation ratio and temperature have significant effects on the crystal nucleation process. Under different conditions, the dominant factor in the nucleation process also changes. When the supersaturation ratio is higher, the solute content in the solution is greater, and there is a greater chance of collision between solute molecules, making nucleation easier and thus leading to a shorter induction time. However, when the supersaturation ratio gradually increases and reaches the high supersaturation region, the effect of solute molecule collision on induction time gradually decreases, and the curve becomes flatter as a result. When the supersaturation ratio increases with decreasing temperature, the supersaturation ratio becomes the dominant factor in the nucleation process, resulting in a shorter time required to induce nucleation. Conversely, when the supersaturation ratio decreases with increasing nucleation temperature, temperature becomes the critical factor, accelerating the nucleation process. Although the supersaturation ratio is the driving force of the crystallization process, it does not always dominate. Both supersaturation ratio and nucleation temperature control the crystallization process.

Fig. 5.

The relationship between the supersaturation ratio and induction period at various temperatures.

Figure 6 shows the relationship between homogeneous and heterogeneous nucleation of K₂SO₄. It can be seen that there is a linear relationship between induction time and supersaturation ratio. The two lines with different slopes correspond to homogeneous and heterogeneous nucleation mechanisms, respectively. Under high supersaturation conditions, the effect of homogeneous nucleation is more significant. When the supersaturation ratio S > 1.22, homogeneous nucleation dominates. On the other hand, when the supersaturation ratio S < 1.20, heterogeneous nucleation dominates. When 1.20 < S < 1.22, the two nucleation mechanisms compete with each other, resulting in a transitional nucleation mechanism state.

Fig. 6.

The plots of ln(${{t}_{{{\text{ind}}}}}$) versus 1/ln²S at different temperatures.

4.1.3. Nucleation parameters. According to Fig. 7, it can be seen that based on the classical nucleation theory, the nucleation parameters can be obtained by substituting γ into Eqs. (17), (18), (22), and (28). As the temperature and supersaturation ratio increase, the critical nucleation free energy ΔG*, critical nucleation radius r*, and critical nucleus size i* all decrease, while the nucleation rate J* increases. These experimental results are consistent with classical nucleation theory, further verifying that both supersaturation ratio and temperature control the nucleation process. Therefore, at a certain temperature, increasing the supersaturation ratio can improve the nucleation rate and shorten the induction time. Compared with temperature, the effect of supersaturation ratio on nucleation is more significant.

Fig. 7.

The relationship between the supersaturation ratio and nucleation parameters at various temperatures ((a) critical nucleation free energy, (b) the number of formula units in the critical nucleiat, (c) the radius of critical nucleus, (d) nucleation rate).

As can be seen from Table 1 above, the surface entropy factor values for nucleation and crystallization of potassium sulfate are all less than 3. Therefore, it is speculated that potassium sulfate crystallizes in a continuous growth mechanism in this system.

Table 1.   The γ and f for homogeneous nucleation of K₂SO₄

4.2 Stirring Crystallization Kinetics

4.2.1. Kinetic data. Figure 8 shows that crystal number density is linearly related to particle size, and it can be assumed that crystal growth rate is independent of particle size. This study adopts a growth model independent of particle size and obtains kinetic parameters through nonlinear regression calculation to finally derive the crystallization kinetic equation:

$$\begin{gathered} {{B}_{0}} = 4.2805 \times {{10}^{5}}\exp \left( { - \frac{{2.433 \times {{{10}}^{4}}}}{{RT}}} \right) \\ \times \;M_{T}^{{1.1672}}\Delta {{C}^{{1.1672}}}N_{P}^{{2.142}}\quad ({{R}^{2}} = 0.954), \\ \end{gathered} $$

(30)

$$\begin{gathered} G = 2.069 \times {{10}^{{ - 5}}}\exp \left( { - \frac{{3.544 \times {{{10}}^{4}}}}{{RT}}} \right) \\ \times \;\Delta {{C}^{{0.2945}}}N_{P}^{{0.9836}}\quad ({{R}^{2}} = 0.912). \\ \end{gathered} $$

(31)

Fig. 8.

The relationship between crystal particle number density and particle size.

Crystal nucleation and growth rates increase with an increase in supersaturation, but nucleation rates increase more rapidly. On the contrary, high supersaturation is not conducive to obtaining crystals of a large average size, because it may lead to faster aggregation of clusters, even leading to severe equipment fouling.

4.2.2. Influence factor. The influence of suspension density on nucleation rate is shown in Fig. 9, where nucleation rate increases with increasing suspension density. The presence of suspended particles in the solution can lead to secondary nucleation of crystalline nuclei and increase the probability of collision between particles. Figure 10 shows the effect of supersaturation on crystal nucleation and growth. Excessive supersaturation can inhibit crystal growth due to significant competition between nucleation and growth. High supersaturation leads to excessively high nucleation rates, insufficient growth space, small particle size, uneven distribution, and poor quality. Choosing an appropriate supersaturation during industrial crystallization can optimize crystal quality.

Fig. 9.

The relationship between nucleation rate and suspension density.

Fig. 10.

The relationship between nucleation, growth rate and supersaturation ratio.

Stirring can directly affect the contact process between crystals and crystals or between crystals and container walls (Fig. 11). When the stirring rate increases, the crystal kinetic rate will also increase. However, increasing the stirring intensity can cause severe collisions between solutes and crystal nuclei, leading to rapid spontaneous nucleation, which is not conducive to growth. The comparison between experimental and calculated rates is shown in Fig. 12, where the mean error between calculated values by Eqs. (30) and (31) and experimental values is 11.14% (Fig. 12a) and 11.27% (Fig. 12b), respectively.

Fig. 11.

The relationship between crystallization kinetic rate and stirring rate.

Fig. 12.

Comparison between experimental and theoretical kinetics rate for Na₂SO₄ crystallization: (a) nucleation rate and (b) growth rate.

5 CONCLUSIONS

(1) As the supersaturation ratio and temperature increase, the induction time decreases. When the supersaturation ratio exceeds 1.22, the effect of temperature on induction time is significant; when the supersaturation ratio reaches 1.20, the change in the supersaturation ratio plays a crucial role in nucleation.

(2) At high supersaturations, i.e., supersaturation ratios of 1.22 and above, homogeneous nucleation dominates; at low supersaturations, i.e., supersaturation ratios of 1.20 and below, heterogeneous nucleation dominates.

(3) As the temperature and supersaturation ratio increase, the critical free energy ΔG*, critical radius r*, and critical number i* for nucleation decrease, while the nucleation rate J* increases. The surface entropy factor is less than 3, indicating that the growth pattern of potassium sulfate in water is a continuous growth mechanism.

(4) Crystals are typically rectangular blocks and are relatively unaffected by temperature and supersaturation. Average particle size increases with increasing supersaturation ratio and crystallization temperature. Increasing crystallization temperature and supersaturation ratio is beneficial to crystal growth and to obtaining large grain crystals.

(5) A growth model independent of nucleation and particle size was obtained based on particle density distribution. Both models show that an increase in supersaturation ratio and temperature leads to an increase in both nucleation rate and growth rate-the increase in suspension density and stirring rate has a significant impact on nucleation rate. Moreover, there is good agreement between experimental and theoretical values.