Using Third-Generation CALPHAD Models to Approximate Thermodynamic Properties of Solid Uranium Diboride

Abstract

Expressions are obtained for the Gibbs energy of solid uranium diboride UB₂ at T = 0–2300 K in the standard element reference system. They are established to describe the experimental data on heat capacity and heat content throughout the range of temperatures with a single dependence. The weighted sum of the Einstein functions with no polynomial contribution is shown to approximate the limit behavior of the heat capacity at T = 1–5 K. A simplified dependence with six parameters is proposed for the Gibbs energy at T = 200–2000 K.

INTRODUCTION

Uranium diboride UB₂ is of interest as a component of promising nuclear fuels resistant to accidents (accident tolerant fuels) [1]. Studies of its thermodynamic properties are important both for optimizing the conditions for fuel production and for predicting phase and chemical equilibria with its participation. The thermodynamic model of a uranium–boron binary system in [2] allows us to obtain the phase diagram and the properties of all binary compounds in it: UB₂, UB₄, and UB₁₂. It belongs to the second-generation CALPHAD models; i.e., it is based on polynomial functions and can be used only when T ≥ 298.15 K. A possible alternative is the third-generation CALPHAD models first proposed in 1995 [3]. The Einstein or Debye functions are used in these models to approximate isobaric heat capacity C_p, ensuring their applicability down to 0 K and the possibility of extrapolating them to both low and high temperatures. Voronin and Kutsenok [4] and Jacobs et al. [5] independently proposed using the weighted sum of several Einstein functions to achieve high accuracy in approximating the heat capacity of complex substances in a wide range of temperatures. This model was supplemented with a polynomial in [6] and used to approximate the heat capacities of graphite and diamond.

There are experimental data on isobaric heat capacity C_p [7] and heat content H_T − H_298.15 [8, 9] for solid uranium diboride UB₂ that cover the 1.1–2300 K range of temperatures. A brief list of these is presented in Table 1. All were obtained for samples of composition UB_1.979. To move to thermodynamic functions of stoichiometric UB₂, we used factor 3/2.979 ≈ 1.007 proposed in [7]. Values of the thermodynamic functions of UB₂ at T = 298.15 K, obtained from experimental data on heat capacity, were recommended in that work: $S_{{298.15}}^{ \circ } = 55.51 \pm 0.11$ J/(mol K), $H_{{298.15}}^{ \circ } - H_{0}^{ \circ } = 8880 \pm 17$ J/mol, and $C_{{p,298.15}}^{ \circ }$ = $55.76 \pm 0.11$ J/(mol K).

Table 1.   Available experimental data on heat capacities and heat contents of UB₂

The enthalpy of formation of uranium diboride ${{{{\Delta }}}_{{\text{f}}}}H_{{298.15}}^{ \circ }({\text{U}}{{{\text{B}}}_{2}}) = - 164.43 \pm 17$ kJ/mol (‒39.3 $\pm$ 4.0 kcal/mol) [7] was obtained by burning a UB₂ sample in a fluorine atmosphere inside a calorimetric bomb, and using literature data on the enthalpies of formation of UF₆ and BF₃.

The temperature dependence of the Gibbs energy for UB₂ at T = 298.15–2300 K [2] in the standard element reference system is presented along with experimental data. The formulas are given in terms of U_1/3B_2/3:

$$\begin{gathered} G(T)-{{H}_{{{\text{SER}}}}},\;{\text{J/mol}} = -63\,972.50 \\ + \;137.55038T-22.286574T\ln T \\ - \;5.157738 \times {{10}^{{ - 3}}}{{T}^{2}} + 0.39417 \times {{10}^{{ - 6}}}{{T}^{3}} \\ + \;310\,100{\text{/}}T\quad (298.15 < T < 1600\;{\text{K}}), \\ \end{gathered} $$

(1)

$$\begin{gathered} G(T)-{{H}_{{{\text{SER}}}}},\;{\text{J/mol}} = -344\,980.46 \\ + \;2063.58552T-283.582964T\ln T \\ + \;106.066517 \times {{10}^{{ - 3}}}{{T}^{2}}-8.73248 \times {{10}^{{ - 6}}}{{T}^{3}} \\ + \;58\,632\,007{\text{/}}T\quad (1600 < T < 2300\;{\text{K}}), \\ \end{gathered} $$

(2)

where H_SER is the reference level, i.e., the enthalpies of formation of simple substances (stable allotropic modifications) at T = 298.15 K and p = 1 bar. The generalized G_T – H_SER expression for an individual compound is

$${{G}_{T}} - {{H}_{{{\text{SER}}}}} = ({{H}_{T}} - {{H}_{{298.15}}} + {{{{\Delta }}}_{{\text{f}}}}H_{{298.15}}^{ \circ }) - T{{S}_{T}},$$

(3)

where ${{{{\Delta }}}_{{\text{f}}}}H_{{298.15}}^{ \circ }$ is the standard enthalpy of formation. For UB₂, we used the value obtained for it in [7] (see above). Disadvantages of this polynomial model are the use of two different dependences for T = 298.15–1600 and >1600 K, along with its unsuitability for calculating C_p at T < 298.15 K. Entropy $S_{{298.15}}^{ \circ }~$ = 54.525 J/(mol K) was used as is (i.e., it cannot be obtained from the C_p(T) polynomial dependence).

No thermodynamic models that allow us to calculate isobaric heat capacity of UB₂ at T = 0–298.15 K are described in the literature. The following approximation of low-temperature C_p for T < 4.2 K was proposed in [7]:

$$\begin{gathered} {{C}_{p}},\;{\text{mJ/}}({\text{mol}}\;{\text{K}}) = (9.40 \pm 0.01)T \\ + \;(3.18 \pm 0.14) \times {{10}^{{-2}}}{{T}^{3}}. \\ \end{gathered} $$

(4)

An approximation of the heat capacity anomaly of solid UB₂ at T = 40–100 K, made using a two-level Schottky model, was proposed in the same work. Unfortunately, these two models do not cover the entire 0–298.15 K range of temperatures and cannot be used to calculate $S_{{298.15}}^{ \circ }$. While the experimental heat capacities were approximated in [7] by polynomial dependences, the dependences themselves are not given.

The aim of this work was to obtain the temperature dependences of the Gibbs energy of solid uranium diboride UB₂, based on the third-generation CALPHAD models and the available experimental data on isobaric heat capacity, heat content, and enthalpy of formation.

CALCULATIONS

Experimental data on heat capacity and heat content were approximated using a model that included a weighted sum of Einstein functions and a polynomial contribution:

$$\begin{gathered} {{C}_{p}}(T,{\boldsymbol{\alpha }},{\boldsymbol{\theta }},{{a}_{1}},{{a}_{2}}) = \mathop \sum \limits_{i~ = ~1}^m \,{{\alpha }_{i}}{{C}_{{\text{E}}}}\left( {\frac{{{{\theta }_{i}}}}{T}} \right) \\ + \;R{{a}_{1}}\left( {\frac{T}{{{{T}_{0}}}}} \right) + R{{a}_{2}}{{\left( {\frac{T}{{{{T}_{0}}}}} \right)}^{4}}, \\ \end{gathered} $$

(5)

$$\frac{{{{C}_{{\text{E}}}}(x)}}{R} = \frac{{3{{x}^{2}}{{e}^{x}}}}{{{{{({{e}^{x}} - 1)}}^{2}}}},$$

(6)

where T₀ = 298.15 K; R is the universal gas constant; m is the number of Einstein functions; and ${{\alpha }_{i}}$, ${{\theta }_{i}}$, a₁, and a₂ are model parameters. This model was proposed in [6] and obtained by adding a polynomial to the model of isobaric heat capacity proposed by Voronin and Kutsenok in [4] and based on the weighted sum of Einstein functions. The polynomial of Eq. (5) differs from the AT + BT⁴ expression used in [6] by dimensionless coefficients a₁ and a₂.

The expressions for entropy and heat content can be obtained by integrating Eq. (6):

$$\begin{gathered} S(T,{\boldsymbol{\alpha }},{\boldsymbol{\theta }},{{a}_{1}},{{a}_{2}}) = \mathop \sum \limits_{i~ = ~1}^m \,{{\alpha }_{i}}{{S}_{{\text{E}}}}\left( {\frac{{{{\theta }_{i}}}}{T}} \right) \\ + \;R{{a}_{1}}\left( {\frac{T}{{{{T}_{0}}}}} \right) + \frac{{R{{a}_{2}}}}{4}{{\left( {\frac{T}{{{{T}_{0}}}}} \right)}^{4}}, \\ \end{gathered} $$

(7)

$$\frac{{{{S}_{{\text{E}}}}(x)}}{R} = 3\left( {\frac{x}{{{{e}^{x}} - 1}} - \ln (1 - {{e}^{{ - x}}})} \right),$$

(8)

$$\begin{gathered} H(T,{\boldsymbol{\alpha }},{\boldsymbol{\theta }},{{a}_{1}},{{a}_{2}}) - {{H}_{0}} = \mathop \sum \limits_{i~ = ~1}^m \,{{\alpha }_{i}}{{H}_{{\text{E}}}}\left( {\frac{{{{\theta }_{i}}}}{T}} \right) \\ + \;RT\left( {\frac{{{{a}_{1}}}}{2}\left( {\frac{T}{{{{T}_{0}}}}} \right) + \frac{{{{a}_{2}}}}{5}{{{\left( {\frac{T}{{{{T}_{0}}}}} \right)}}^{4}}} \right), \\ \end{gathered} $$

(9)

$$\frac{{{{H}_{{\text{E}}}}(x)}}{{RT}} = \frac{{3x}}{{{{e}^{x}} - 1}}.$$

(10)

The expression for the Gibbs energy in the standard element reference system can be obtained by substituting Eqs. (7)–(10) into Eq. (3):

$$\begin{gathered} G(T,{\boldsymbol{\alpha }},{\boldsymbol{\theta }},{{a}_{1}},{{a}_{2}}) - {{H}_{{{\text{SER}}}}} = {{{{\Delta }}}_{{\text{f}}}}H_{{298.15}}^{ \circ } \\ - \;({{H}_{{298.15}}} - {{H}_{0}}) + \mathop \sum \limits_{i~ = ~1}^m \,{{\alpha }_{i}}{{G}_{{\text{E}}}}\left( {\frac{{{{\theta }_{i}}}}{T}} \right) \\ - \;RT\left( {\frac{{{{a}_{1}}}}{2}\left( {\frac{T}{{{{T}_{0}}}}} \right) + \frac{{{{a}_{2}}}}{{20}}{{{\left( {\frac{T}{{{{T}_{0}}}}} \right)}}^{4}}} \right), \\ \end{gathered} $$

(11)

$$\frac{{{{G}_{{\text{E}}}}(x)}}{{RT}} = \frac{{{{H}_{{\text{E}}}}(x)}}{{RT}} - \frac{{{{S}_{{\text{E}}}}(x)}}{R} = 3\ln (1 - {{e}^{{ - x}}}).$$

(12)

Four versions of the above model were used to approximate experimental data.

The first was model Ein with no polynomial (i.e., ${{a}_{1}} = {{a}_{2}} = 0$ in Eqs. (5), (7), (9), and (11)), the parameters of which were obtained using all of the experimental data in Table 1.

The second was model EinLT with no polynomial. Only data on interval T = 0–1486 K were used in optimizing its parameters.

The third was model EinPoly with a polynomial (i.e., ${{a}_{1}} \ne 0$ and ${{a}_{2}} \ne 0$) based on the same data as model Ein.

The fourth was simplified model Ein2 with two Einstein functions and a polynomial based on the data for T = 200–2300 K, along with values $S_{{298.15}}^{ \circ }$ and $H_{{298.15}}^{ \circ } - H_{0}^{ \circ }$ obtained using model Ein.

The model parameters were optimized using nonlinear least squares in the CpFit program [10]. An objective function based on a weighted sum of the squares of relative deviations was used for the first three models:

$$\begin{gathered} RSS = \mathop \sum \limits_{k~ = ~1}^{{{n}_{C}}} \,\omega _{{C,k}}^{2}{{\left( {\frac{{C_{p}^{{{\text{calc}}}}({{T}_{k}}) - C_{{p,k}}^{{{\text{exp}}}}}}{{C_{{p,k}}^{{{\text{exp}}}}}}} \right)}^{2}} \\ + \;\mathop \sum \limits_{k~ = ~1}^{{{n}_{H}}} \,\omega _{{H,k}}^{2}{{\left( {\frac{{{{\Delta }}{{H}^{{{\text{calc}}}}}({{T}_{k}}) - {{\Delta }}H_{k}^{{{\text{exp}}}}}}{{{{\Delta }}H_{k}^{{{\text{exp}}}}}}} \right)}^{2}}, \\ \end{gathered} $$

(13)

where indices calc and exp denote calculated and experimental values, and ω_С and ω_H are the statistical weights for isobaric heat capacities and heat contents, respectively: ω_С = 1 for T ≥ 5 K and ω_С = 0.25 for T < 5 K. Unit statistical weights of ω_H = 1 were used in all models except Ein2, where ω_H = 1 and 0.1 for points from [8] (T = 479–1486 K) and [9] (T = 1303–2300 K), respectively. For simplified model Ein2 with two Einstein functions and a polynomial, experimental data were used exclusively for T > 100 K. The reproducibility of $S_{{298.15}}^{ \circ }$ and $H_{{298.15}}^{ \circ } - H_{0}^{ \circ }$ was ensured by introducing two additional terms into the objective function (i.e., using a new RSS₂ objective function):

$$\begin{gathered} RS{{S}_{2}} = RSS + {{10}^{4}}{{\left( {\frac{{S_{{298.15}}^{{ \circ ,{\text{calc}}}} - S_{{298.15}}^{{ \circ ,{\text{ref}}}}}}{{S_{{298.15}}^{{ \circ ,{\text{ref}}}}}}} \right)}^{2}} \\ + \;{{10}^{4}}{{\left( {\frac{{{{\Delta }}{{H}^{{ \circ ,{\text{calc}}}}} - {{\Delta }}{{H}^{{ \circ ,{\text{ref}}}}}}}{{{{\Delta }}{{H}^{{ \circ ,{\text{ref}}}}}}}} \right)}^{2}}, \\ \end{gathered} $$

(14)

where RSS is the objective function described by Eq. (13), and superscripts calc and ref refer to values obtained from models Ein2 and Ein, respectively. When optimizing the parameters of model Ein2, additional condition $\sum\nolimits_i^{} {{{\alpha }_{i}}} = {{N}_{{{\text{atoms}}}}}$ = 3 implemented in the CpFit program by a change of variables was used as well:

$$\left\{ \begin{gathered} {{\alpha }_{1}} = (1 - {{\xi }_{1}}){{N}_{{{\text{atoms}}}}} \hfill \\ {{\alpha }_{2}} = {{\xi }_{1}}{{N}_{{{\text{atoms}}}}}, \hfill \\ \end{gathered} \right.$$

(15)

where ${{\xi }_{1}} \in \left[ {0;\,\,1} \right]$ is the parameter to be optimized, and ${{N}_{{{\text{atoms}}}}} = 3$.

Two values were used to estimate the accuracy of the experimental data approximation: the standard deviation and the normalized median absolute deviation. They were calculated for the absolute and relative deviations as

$$\begin{gathered} s(\delta Y) = \sqrt {\frac{{\sum\limits_{i~ = ~1}^n {{{{(Y_{i}^{{{\text{calc}}}} - Y_{i}^{{{\text{exp}}}})}}^{2}}} }}{n}} ; \\ s(\varepsilon Y) = \sqrt {\mathop \sum \limits_{i~ = ~1}^n \,{{n}^{{ - 1}}}{{{\left( {\frac{{Y_{i}^{{{\text{calc}}}} - Y_{i}^{{{\text{exp}}}}}}{{Y_{i}^{{{\text{exp}}}}}}} \right)}}^{2}}} ; \\ \end{gathered} $$

(16)

$$\begin{gathered} {{s}_{{{\text{MAD}}}}}(\delta Y) = \frac{{\operatorname{median} ~\left| {Y_{i}^{{{\text{calc}}}} - Y_{i}^{{{\text{expt}}}}} \right|}}{{{{{{\Phi }}}^{{ - 1}}}(0.75)}}; \\ {{s}_{{{\text{MAD}}}}}(\varepsilon Y) = \frac{{\operatorname{median} ~\left| {\frac{{Y_{i}^{{{\text{calc}}}} - Y_{i}^{{{\text{expt}}}}}}{{Y_{i}^{{{\text{expt}}}}}}} \right|}}{{{{{{\Phi }}}^{{ - 1}}}(0.75)}}, \\ \end{gathered} $$

(17)

where $Y$ is isobaric heat capacity C_p or heat content ${{H}_{T}} - {{H}_{{298.15}}}$, and ${{{{\Phi }}}^{{ - 1}}}(x)$ is the inverse cumulative distribution function for standard normal distribution $1{\text{/}}{{{{\Phi }}}^{{ - 1}}}(0.75) \approx 1.483$. A more detailed description of these estimates of the accuracy of approximation, including the rationale for using normalizing factor 1.483, was given in [11] on the use of the CpFit program for compiling databases.

RESULTS AND DISCUSSION

The resulting sets of parameters for Eqs. (5)–(12) are presented in Table 2. The parameters below were obtained for simplified model Ein2:

$$\begin{gathered} {{\alpha }_{1}} = 1.96081,\quad {{\alpha }_{2}} = 1.03919, \\ {{\theta }_{1}}{\text{/K}} = 855.158,\quad {{\theta }_{2}}{\text{/K}} = 181.689, \\ {{a}_{1}} = 0.609182,\quad {{a}_{2}} = 1.88976 \times {{10}^{{ - 5}}}. \\ \end{gathered} $$

(18)

Table 2.   Optimized model parameters α_i, θ_i, a₁, and a₂ for the weighted sum of Einstein functions with and without a polynomial (see Eqs. (5), (7), (9), and (11))

Tables 3 and 4 show the accuracy of approximating experimental data on isobaric heat capacity [7] and heat content [8, 9] using different thermodynamic models: those obtained in this work and taken from [1]. The two temperature ranges in the data from [7] correspond to samples obtained by isoperibol and adiabatic calorimetry (see Table 1).

Table 3.   Accuracy of approximating experimental data on heat capacity from [7] (see Table 1) using different models

Table 4.   Accuracy of approximating experimental data on heat content from [8, 9] (see Table 1) using different models

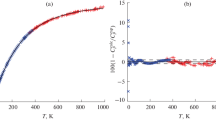
Figures 1 and 2 show results from approximating experimental data on isobaric heat capacity and heat content. The temperature dependences of C_p and H_T – H_298.15 are shown in Figs. 1a and 2a, and the corresponding scatter plots are shown in Figs. 1b and 2b.

Fig. 1.

Results from approximating experimental values of the isobaric heat capacity of UB₂: (a) dependences of C_p on T; (b) dependences of relative deviations $\varepsilon {{C}_{p}} = 100(C_{p}^{{{\text{expt}}}} - C_{p}^{{{\text{calc}}}}){\text{/}}C_{p}^{{{\text{expt}}}}$ on T. The solid, dashed, dashed-and-dotted, and dotted lines are models Ein, EinPoly, Ein2, and Poly, respectively. Dots are experimental values of C_p from [7]; rings and triangles are data from isoperibol and adiabatic calorimetry, respectively.

Fig. 2.

Results from approximating experimental values of the heat content of UB₂: (a) the dependence of ${{\Delta }}H = ({{H}_{T}} - {{H}_{{{{T}_{0}}}}}){\text{/}}(T - {{T}_{0}})$ on T, T₀ = 298.15 K; (b) the dependence of relative deviations $\varepsilon {{\Delta }}H = 100({{\Delta }}{{H}^{{{\text{expt}}}}} - {{\Delta }}{{H}^{{{\text{calc}}}}}){\text{/}\Delta }{{H}^{{{\text{expt}}}}}$ on T. The bold, fine, dashed, dashed-and-dotted, and dotted lines show data obtained using models Ein, EinLT, EinPoly, Ein₂, and Poly, respectively. Dots are experimental data obtained via drop calorimetry; diamonds and squares are values from [8] and [9], respectively.

Files of the initial data and obtained model parameters are available at https://doi.org/10.17632/3vkpz6nfff.1 as the Mendeley Data Set for the CpFit and GNU Octave programs for plotting and tables.

Model Ein with nine Einstein functions and no polynomial with 18 optimized parameters turned out to be the most accurate of those obtained in this work. In it, $\sum\nolimits_i^{} {{{\alpha }_{i}}} \gg {{N}_{{{\text{atoms}}}}} = 3$. This because with no polynomial, difference C_p – C_V, the anharmonicity of lattice vibrations, and the growth of C_p before melting are approximated by Einstein functions with values of ${{\alpha }_{i}}$ and ${{\theta }_{i}}$, which have no explicit physical meaning. This was observed in [10] for uranium dioxide UO₂.

Adding a polynomial to model EinPoly allowed us to approximately meet condition $\sum\nolimits_i^{} {{{\alpha }_{i}}} \approx {{N}_{{{\text{atoms}}}}}$ for UB₂ and reduce the number of Einstein functions to five, and the number of model parameters to 12 (Table 2). It also improved the limit behavior of the model at T < 1 K (see Fig. 1a). Models Ein and EinPoly in this case have comparable accuracy throughout the T = 1–2300 K range of temperatures, and the differences when T < 1 K do not affect the values of $S_{{298.15}}^{ \circ }$ and ${{H}_{T}} - {{H}_{{298.15}}}$ appreciably. Condition $\sum\nolimits_i^{} {{{\alpha }_{i}}} \approx {{N}_{{{\text{atoms}}}}} = 3$ was met approximately for model EinLT by excluding data on heat content when T > 1486 K. This allowed us to reduce the number of Einstein functions to eight, and the number of parameters to 16. It also reduced the accuracy of approximating the experimental values of H_T – H_298.15 from [8] (T = 1303–2300 K).

Models Ein, EinLT, and EinPoly obtained in this work describe the heat capacity of UB₂ more accurately than the polynomial model available in [2]. They are not inferior to it in terms of approximating heat content, but the first two require more optimized parameters. The polynomial model in [2] has only 12 parameters: six for each temperature interval (see Eqs. (1) and (2)). To test the possibility of reducing their number, we constructed simplified model Ein2 with six parameters that included two Einstein functions and a polynomial. Its accuracy was comparable to models Ein, EinLT, and EinPoly at T = 200–2000 K with fewer parameters. Its accuracy fell notably outside this range (see Figs. 1, 2), but the values it produced remained physically correct.

The tabulated values of the thermodynamic functions of solid uranium diboride UB₂ when T = 1–2300 K are given in Table 5. They were calculated using model Ein (i.e., the one based on the weighted Einstein function with no polynomial), since it was more accurate than the others, including the polynomial model described in [2]. The values of $C_{{p,298.15}}^{ \circ }$, $S_{{298.15}}^{ \circ }$, and ${{H}_{T}} - {{H}_{{298.15}}}$ obtained from all four models constructed in this work coincided within their confidence intervals. They also agreed with the data in [7].

Table 5.   Thermodynamic functions of uranium diboride UB₂, calculated using model Ein (see Eqs. (5), (7), (9), (11), and their parameters in Table 2)

CONCLUSIONS

Thermodynamic models based on the weighted sum of Einstein functions allowed us to approximate experimental data on the heat capacity and heat content of solid uranium diboride throughout the 1–2300 K range of temperatures. Adding a polynomial of the AT + BT⁴ form to dependence C_p(T) did not improve the accuracy of approximation. However, it did reduce the number of model parameters, allowed us to meet condition $\sum\nolimits_{i~ = ~1}^m {{{\alpha }_{i}}} = {{N}_{{{\text{atoms}}}}}$ approximately, and improved the limit behavior of function C_p(T) when T → 0 K. A simplified thermodynamic model with two Einstein functions and a polynomial can be used when T = 200–2000 K. It produces physically correct heat capacities when extrapolated to high and low temperatures, along with accurate values of $C_{{p,298.15}}^{ \circ }$, $S_{{298.15}}^{ \circ }$, and ${{H}_{T}} - {{H}_{{298.15}}}$. Its advantages over the polynomial model of [2] are half the number of parameters, no piecewise specified functions, and physically correct behavior when extrapolated to low temperatures.