INTRODUCTION

The question of the effect the limited volume of a system has on phase transitions has always been of interest. As system sizes shrink, discrete properties of molecules begin to manifest, and the equations of classical thermodynamics are violated [1–10]. This has been known since Gibbs’s work on statistical mechanics [1], but the effect the limited volume of a system has on its thermodynamic state has barely been studied. The main focus has always been on small bodies surrounded by a macroscopic environment. In small bodies, the surface makes an appreciable contribution to the total free energy of a body, and contributions from its interior and surface become comparable. Liquid droplets in a supersaturated vapor and bubbles in liquid phases, microcrystals, micelles, colloidal particles, polymeric particles in liquid phases, inclusions in solid-phase systems, and so on have traditionally been ascribed to them.

General approaches to studying small systems were developed in [10, 11]. One of the considered questions corresponds to a situation with a limiting external boundary/wall through which energy can be exchanged (with a constant temperature maintained in the system), but not momentum and matter. Phase transitions inside the limited area are naturally interpreted in analogy with macroscopic systems, since the conditions of constant temperature, pressure, and chemical potential stem from kinetic consideration of the molecular redistribution, rather than being inherent to macroscopic systems only. The potential of a limiting wall (Qw > 0 or <0) reflecting its chemical and structural heterogeneity along with the characteristic size of the system plays an important role in the molecular distribution. In [9], these factors were considered in detail inside pores. The heterogeneity of the walls results in the possible emergence of a set of critical points in the curves of vapor–fluid phase separation in both porous bodies and open heterogeneous surfaces.

The phase transition with phase separation of a one-component compound was considered in [12]. Phase separated mixtures should behave in a similar manner, but phase transitions of the ordering type have yet to be discussed. As in [10, 11], we limit ourselves to the simplest case and consider a monodisperse system of limited elementary volumes, inside which there are components of a binary А + В mixture in a 1 : 1 ratio. For simplicity, we also assume that the specific volumes of components are comparable and their differences can be ignored. Finally, we limit ourselves to considering the mean values of thermodynamic functions to eliminate the effect of size fluctuations [10].

To describe local molecular distributions, we use a discrete version of the lattice gas model (LGM) [13]. The concentration of component i is characterized by the value θi = Ni/М. The relationship between the generally accepted (where ni is the number of particles in a unit volume) and lattice concentrations of i-type particles is written as θi = ni\({{{v}}_{0}}\). The local density of i‑type particles at a site with number g is denoted as \(\theta _{g}^{i}\). The local densities are normalized: \(\sum\nolimits_{i = 1}^s {\theta _{g}^{i} = {\text{ }}1} \). The average concentration of the i component of the θi system is defined through local concentrations as \({{\theta }_{i}} = \sum\nolimits_{q = 1}^t {{{f}_{q}}\theta _{q}^{i}} \), where fq = Mq/M is the fraction of q‑type sites; \(\theta _{q}^{i}\) = \(N_{q}^{i}\)/Mq are the partial local occupancies, and \(N_{q}^{i}\) is the number of i-type molecules at q‑type sites. The number of vacant sites of the q type we denote as \(N_{q}^{V} = {\text{ }}{{M}_{q}} - \sum\nolimits_{i = 1}^{s - 1} {N_{q}^{i}} \). The total number of sites in system М consisting of parts with size Mq, is 1 ≤ q ≤ t, where t is the number of site types: M = \(\sum\nolimits_{q = 1}^t {{{M}_{q}}} \) or \(\sum\nolimits_{q = 1}^t {{{f}_{q}} = 1} \).

The number of the sites nearest to this site in the lattice structure is designated as z. We believe that lateral interaction is described by the Lennard–Jones (L–D) pair potential: \(\varepsilon _{{gh}}^{{ij}}(r)\) = \({\text{4}}{{\varepsilon }_{{ij}}}\{ {{({{\sigma }_{{ij}}}{\text{/}}r_{{gh}}^{{ij}})}^{{{\text{12}}}}} - {{({{\sigma }_{{ij}}}{\text{/}}r_{{gh}}^{{ij}})}^{{\text{6}}}}\} \) (where \(r_{{gh}}^{{ij}}\) are the distances between particle pairs ij at different sites g and h) with a radius of interaction of unity. There is no interaction between particles and vacancies.

Let us consider the simplest ordered system formed of two interpenetrating sublattices in a simple cubic lattice (z = 6) and a body-centered cubic lattice (z = 8) of the β-brass type [13–15]. The first sublattice, the sites of which are usually occupied, is denoted as α; the second, whose sites are mainly unoccupied, is denoted as γ. Each site of the α-sublattice is surrounded by sites of the γ-sublattice, and vice versa. This allows us to determine the ordered state of particles from the distribution functions of sites of different types that were introduced in [13]: fα = fγ = 1/2 and zαγ = zγα = z.

We denote through θσ (σ = α, γ) the probability of σ-type sites being occupied. Equations for the local occupancies of sites of different types in a homogeneous bulk phase (internal degrees of freedom of particles and their interaction parameters do not depend on the type of the sublattice site) are written as [13]

$$y = \frac{{{{\theta }_{\alpha }}}}{{1 - {{\theta }_{\alpha }}}}{{(1 + {{t}_{{\alpha \gamma }}}x)}^{z}},\quad y = \frac{{{{\theta }_{\gamma }}}}{{1 - {{\theta }_{\gamma }}}}{{(1 + {{t}_{{\gamma \alpha }}}x)}^{z}},$$
$$\begin{gathered} x = \exp ( - \beta \omega ) - 1,\quad {{\theta }_{{\alpha \gamma }}} = 2{{\theta }_{\alpha }}{{\theta }_{\gamma }}{\text{/}}(\delta + b), \\ {{t}_{{\lambda \sigma }}} = {{\theta }_{\alpha }}_{\gamma }{\text{/}}{{\theta }_{\lambda }},\quad \lambda \ne \sigma ,\quad \delta = 1 + x(1 - {{\theta }_{\alpha }} - {{\theta }_{\gamma }}), \\ \end{gathered} $$
(1)
$$b = {{({{\delta }^{2}} + 4x{{\theta }_{\alpha }}{{\theta }_{\gamma }})}^{{1/2}}}.$$

The isotherm of adsorption is θ = (θα + θγ)/2, where θσ is found from the set of Eqs. (1).

If y is excluded from Eq. (1), we obtain the equation relating relative site occupancies θα and θγ. With regard to θγ = 2θ − θα, this equation with one or three roots allows us to calculate θα(θ, βε). In the first case, there is no ordering of particles in the system. In the second, the larger root corresponds to θα; the smaller one, to θγ. The temperature below which the formation of the ordered state is possible is called the temperature of ordering. Its value is found by expanding in series the equation relating site occupancies α and γ in terms of small ordering parameter ρ, which characterizes the fraction of particles at α sublattice sites: θα = θ + ρ (1 – θ), θγ = θ – ρ (1 – θ). If all particles are at α sublattice sites, then ρ = 1 and θα = 1. Parameters ρ = 0 and θα = θγ = θ correspond to the disordered state. Limiting ourselves to the first terms of the series expansion at ρ = 0, we obtain the relationship between the critical particle concentrations and the temperature of ordering: 1 + х + b = 2zxθ(1 – θ). In the special case of half-occupancy, we have βε = –2ln(1 – 2/z). In the low-temperature range (βε → ∞), the limiting values of the degrees of occupancy limiting the area of existence of this ordered state are θ = 1/z.

Let us consider a domain in bulk lattice z = 6 with six faces and a cube shape with side Ld. Altogether, the domain contains (Ld)3 sites. The averaged L–J potential (12-6) of the wall yields potential (9-3) [9], which acts on rs monolayers. The wall field in the first monolayer has potential Qw , and the wall field potential diminishes as 1 : 0.21 : 0.6 : 0.3 : 0.1 upon moving from the wall of the first monolayer to the fifth one. At the same time, ns wall fields (0 ≤ ns ≤ 3) can act on the site, and their potentials act additively. The opposite cube walls have the same potential, and the domain has central symmetry relative to the center of the cube, allowing the reduction of site types and the dimensionality of the problem.

As above, the ordering of А and В components is reflected through the functions of sites of different types [13]. The fraction of sites at the cube vertices where they are subjected to the action of the field from three walls at once is \({{f}_{{v}}}\) = 8(rs)3/(Ld)3. The vertices contain the same number of sites (rs)3 of α and γ lattices. The fraction of sites of a separate type at the vertices is fq = 4/(Ld)3. The fraction of sites at the cube edges where the field from two walls acts on them is fe = 4(rs)2(Ld – 2rs)/(Ld)3. The edges have (rs)2 types of the α lattice sites and the same number of types of γ lattice sites. The fraction of sites of a separate type on the edges is fq = 2(Ld – 2rs)/(Ld)3. The fraction of sites on the cube faces where the field from one wall acts on them is fe = 2rs(Ld – 2rs)2/(Ld)3. The fraction of sites of a separate type on the faces is fq = (Ld – 2rs)2/(Ld)3. Finally, the fraction of sites inside the cube where the field of walls do not act on them is fe = (Ld – 2rs)3/(Ld)3. As in the bulk, there are two types of sites of the α and γ lattices. The fraction of sites in the center of the cube is fq = (Ld – 2rs)3/2(Ld)3.

The fraction of sites in the domain of given type q to which a certain number ns corresponds is thus \({{f}_{q}}({{n}_{s}}) = \frac{{{{{(2)}}^{{{{n}_{s}}}}}{{{({{L}_{d}} - 2{{r}_{s}})}}^{{3 - {{n}_{s}}}}}}}{{2L_{d}^{3}}}\). The factor of two in the denominator is due to there being two sublattices (α and γ) and \({{\left( 2 \right)}^{{{{n}_{s}}}}}\) is a factor related to the types of sites on the opposite walls coinciding. This factor reflects the property of symmetry and increases the weight of the types of sites considered to be identical because of it. Using this distribution function, we performed the calculations for different lengths of sides of the Ld domain and the areas of the wall potential effect rs. The equations for this heterogeneous system were described in detail in [9, 13].

CALCULATION RESULTS

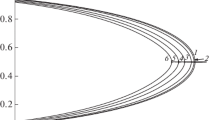
Figure 1 illustrates how the fraction of the internal part of the cube on which the wall effect does not act (fL) depends on the Ld domain size for different widths of the near-wall regions rs. At Ld = 104, all curves nearly coincide with an accuracy of less than a fraction of one percent. From Ld = 103 and lower, the sites on the domain surface and in the near-surface region start to make up a significant fraction.

Fig. 1.
figure 1

Dependence of fL on Ld domain size at rs = (1) 1, (2) 3, (3) 5.

Full size image

Figure 2 shows critical temperature Tcr inside the domain (the normalized curve in logarithmic coordinates on the abscissa for Qw = 0 from Ld = 20 to 104). It falls along with the size of Ld. This curve corresponds to when the volume is limited by a neutral border: it limits only the number of bonds directed from the domain toward the border without distorting its energy state. The result is that when the domain size rises to Ld = 20 and there is no wall potential, the critical temperature inside domain Tcr(L) drops to 2%, compared to critical temperature Tcr(bulk) in the bulk. Compared to similar changes in phase transitions (of the first order) with phase separation [9], this is a much lower value (ordering is the second order phase transition).

Fig. 2.
figure 2

Dependence of the normalized critical temperature of ordering in the domain with size Ld, compared to the one in the bulk phase Tcr(bulk). (See comments in the text.)

Full size image

The inset in Fig. 2 depicts the curves for all three wall potentials in a narrower range along the abscissa: 20 ≤ Ld ≤ 200 at rs = 5 and Qw = –2|εAA| (triangles), 0 (squares), 2|εAA| (dots). A comparison to Fig. 1 reveals that the ordering is preserved even at relatively large fractions of near-wall sites. This is due to the rigidity of the ordered structure, and the introduction of relatively small perturbations Qw from the walls maintains the ordering (neighbors at the border for lattice z = 6 affect each displaced particle А, which is 4|εAA|). The emergence of the wall potential, both positive Qw = 2|εAA| (attraction) and negative Qw = –2|εAA| (repulsion), lowers the critical temperature even more in comparison to Qw = 0 (to 6 and 3.5% of the critical temperature Tcr(bulk) in the bulk).

RESULTS AND DISCUSSION

Our curves demonstrate the effect size (system volume) has on the critical temperature of the order–disorder phase transition. We managed to obtain the curves using the calculation procedure for the molecular distributions of components in a binary mixture with equimolar composition. This procedure was developed for the theory of heterogeneous condensed systems within the LGM [13]. This model describes discrete configurations of mixture components in three-dimensional solutions and/or alloys, and processes of in two-dimensional adsorption. The one-to-one correspondence between components А and В (the theory of solutions) with the occupied and unoccupied states of lattice sites (the theory of adsorption) makes our results common with an accuracy up to the designation of model parameters.

However, the same model the (so-called Ising model) is known to be used in static thermodynamics to interpret the experimental data on magnetics (any z) [16, 17] and KDP-type ferroelectrics (z = 6) [18, 20]. In the case of magnetics, up or down spin corresponds to occupied and unoccupied states of lattice sites (for which the spin ordering effects reflect the antiferromagnetic states). In the case of ferroelectrics, there is correspondence between oppositely directed spins in magnetics with two proton positions in the hydrogen bond relative to the two oxygen atoms that form it [18–20].

It should be noted that the procedure for deriving equations in the LGM [13] accurately reflects all types of heterogeneities that can occur in real condensed phases: point defects, interfaces, structural changes, and so on. This is its advantage over the traditional research techniques for magnetics and ferroelectrics, due to the possibility of considering changes in the properties of solids at the microscopic level. The experimental data on magnetics give grounds to assume [21] that the transitional regions of domain interfaces are long, and local properties are not very important for them. However, the experimental data on ferroelectrics indicate narrow transitional regions [22], and local properties could be much more important for them. It is worth noting that there are still no theoretical approaches to the statistical theory of domains in ferroelectrics. The dependences of critical temperatures on domain sizes, and the considerable effect the properties of boundaries have on these dependences, described in the present work could be the first step in developing a theory of the formation of domain structure in ferroelectrics and its analysis.