INTRODUCTION

This work is part of the general program being conducted by the author and colleagues, Thermodynamic Properties of Substances with Negative Coefficients of Thermal Expansion and Negative Grüneisen Coefficients. The program is based on the assertion that the thermodynamic derivative of entropy with respect to pressure on the isotherm of \({{\left( {{{\partial S} \mathord{\left/ {\vphantom {{\partial S} {\partial p}}} \right. \kern-0em} {\partial p}}} \right)}_{T}} = - {{\alpha }_{p}}V\), where αp = \({1 \mathord{\left/ {\vphantom {1 V}} \right. \kern-0em} V}{{\left( {{{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial T}}} \right. \kern-0em} {\partial T}}} \right)}_{p}}\) is the isobaric coefficient of thermal expansion and V is volume, cannot always be negative, as is seen for most substances in different states at \({{\alpha }_{p}} > 0\). This view of properties was stated by Bridgman in [1]: “If the total entropy of a body is limited and at T = 0 is zero, as required by the third law of thermodynamics, then the drop in entropy caused by the application of any pressure cannot be greater than the total entropy of the body….”

This problem is of a fundamental nature. Additional interest in this topic is associated with the publication of two articles in Physics—Uspekhi in 2012 [2, 3]. In the first article, Medvedev and Trunin [2] explained the nonconventional behavior of shock adiabats of the compression of porous metals and silicates (primarily SiO2) in the region of high temperatures and pressures and suggested that states with a negative Grüneisen coefficient emerge in this situation. In his response, Brazhkin [3] pointed out the problems of analyzing the considered experimental data, i.e., the complex character of the behavior of silica upon shock-wave compression (structural transformations, the kinetics of the process). In addition, the range of substances in the liquid and amorphous states, the structural transformations in which can be accompanied by the emergence of negative thermodynamic coefficients, were discussed in [3].

In thermodynamics, the Maxwell equations and three derivatives of the heat capacity Cp = \(T{{\left( {{{\partial S} \mathord{\left/ {\vphantom {{\partial S} {\partial T}}} \right. \kern-0em} {\partial T}}} \right)}_{p}}\), compressibility coefficient \({{\beta }_{S}} = - {1 \mathord{\left/ {\vphantom {1 V}} \right. \kern-0em} V}{{\left( {{{\partial V} \mathord{\left/ {\vphantom {{\partial V} {\partial p}}} \right. \kern-0em} {\partial p}}} \right)}_{S}}\), and the coefficients of thermal expansion αp make up a system of differential equations of the second order. According to the conditions of the system’s stability, the first two coefficients are positive, while the CTE can assume negative values. At this stage, when dealing with the problem of negative thermodynamic coefficients, we consider the case where the coefficient of thermal expansion (CTE) is zero; i.e., \({{\alpha }_{p}} = 0\). CTE is included in the expressions for many thermodynamic coefficients, and its zero values are reference points in the isolines of a number of thermodynamic functions and derivatives. For example (and this is of fundamental importance to us), \({{\left( {{{\partial S} \mathord{\left/ {\vphantom {{\partial S} {\partial p}}} \right. \kern-0em} {\partial p}}} \right)}_{T}} = - {{\alpha }_{p}}V\). In addition, zero values emerge for the isochore slope \({{\left( {{{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial T}}} \right. \kern-0em} {\partial T}}} \right)}_{V}} = {{{{\alpha }_{p}}} \mathord{\left/ {\vphantom {{{{\alpha }_{p}}} {{{\beta }_{T}}}}} \right. \kern-0em} {{{\beta }_{T}}}}\), for the Grüneisen coefficient \(\gamma = V{{\left( {{{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial u}}} \right. \kern-0em} {\partial u}}} \right)}_{V}}\) = \({{{{\alpha }_{p}}V} \mathord{\left/ {\vphantom {{{{\alpha }_{p}}V} {\left( {{{\beta }_{T}}{{C}_{V}}} \right)}}} \right. \kern-0em} {\left( {{{\beta }_{T}}{{C}_{V}}} \right)}}\), where u is the internal energy; and for the adiabatic thermal pressure coefficient (ATPC) \({{\left( {{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial p}}} \right. \kern-0em} {\partial p}}} \right)}_{S}} = {{{{\alpha }_{p}}VT} \mathord{\left/ {\vphantom {{{{\alpha }_{p}}VT} {{{C}_{p}}}}} \right. \kern-0em} {{{C}_{p}}}}\). At \({{\alpha }_{p}} = 0\), the values of the isobaric and isochoric heat capacities \({{C}_{p}} = {{C}_{V}} + {{\alpha _{p}^{2}VT} \mathord{\left/ {\vphantom {{\alpha _{p}^{2}VT} {{{\beta }_{T}}}}} \right. \kern-0em} {{{\beta }_{T}}}}\) and the coefficients of the isothermal and adiabatic compressibility of βT and βS coincide. The speed of sound can in this case be calculated according the Newton equation, using the isothermal compressibility coefficient and so on.

Dense water in the normal and supercooled state is a testing field for demonstrating the behavior of thermodynamic properties at zero CTE values. In this work, we focus on determining the boundaries of the entrance and exit to the region of negative CTEs.

ZERO VALUES OF ATPC

It has been known since ancient times that when a body is rapidly deformed or when a fluid is compressed, their bulk temperature temporarily rises. However, only in 1857 did Thomson [4], based on the principle of heat and work equivalence, obtain the relationship between the differentials of pressure and temperature when there is no exchange of heat with the environment. In modern terms, this takes the form of

$$\Delta T = \left( {{{{{\alpha }_{p}}VT} \mathord{\left/ {\vphantom {{{{\alpha }_{p}}VT} {{{C}_{p}}}}} \right. \kern-0em} {{{C}_{p}}}}} \right)\Delta p,\quad dS = 0.$$
((1))

The existence of a density maximum in a water isobar was already known at that time, as was reflected in the ATPC estimates given at 10 atm [4]: \(t = 3.95^\circ {\text{C}}\), \(\Delta T = 0\). At \(t = 0^\circ {\text{C}}\), the estimate of \(\Delta T\) = −0.005 K; i.e., Thomson first obtained a negative value of ATPC. A year later, Joule [5] published experimental data on adiabatic water compression at ~35 atm in the temperature range of 1.2–40°C and confirmed Thomson’s theoretical result. At \(t = 1.2^\circ {\text{C}}\), the experimental value of \({{\Delta T} \mathord{\left/ {\vphantom {{\Delta T} {\Delta p}}} \right. \kern-0em} {\Delta p}} = - 0.22{\text{ }} \times \,\,{\text{1}}{{{\text{0}}}^{{ - 3}}}\) K/atm, which is within 10% of the current data in, e.g., [6]. The experimental Thomson–Joule procedure associated with recording the temperature response under the action of a specific pressure gradient along the adiabatic curve is used under a variety of names to determine, e.g., the heat capacity of a liquid if its CTE is known [7]; or to find the CTE if the heat capacity is known [8, 9].

Let us note here the series of experimental ATPC studies performed by Boehler et al. in 1977–1992 for a large group of substances in the solid and liquid state (metals, including alkali metals and mercury; oxides; hydrocarbons; and water) at low temperatures, and at pressures mostly up to 2–3 GPa with 20–30% compression of the substances [8, 9]. The authors observed a drop in the CTE by a factor of 5–6 for metals and oxides when compressed along isotherms [9]. However, the possibility of negative CTE values emerging at higher compression ratios was not considered in these studies.

We should also note the experimental work of 1992 [10] devoted to determining the maxima of the density of fresh and salt water in isobars in the temperature range of −4.9 to 4°C by means of ATPC. The authors measured temperature response ΔT upon the adiabatic compression of water along isotherms in the pressure range of 1–38 MPa and determined the pressures at which the values of ΔT, and thus αp (see Eq. (1)), are zero. The results from these experiments for water (36 points) are represented by the equation

$$\begin{gathered} {{t}_{{\max d}}} = 3.982 - 0.2004p\left( {1 + 0.00402p} \right), \\ [{{t}_{{\max d}}}] = {^\circ\text{C}},\quad [p] = {\text{MPa}}{\text{.}} \\ \end{gathered} $$
((2))

Below, we use these data in plotting a line of maxima for the density of normal and supercooled water.

The results from physical research and information about our immediate environment intersect in an amazing way. In Antarctica, a subglacial lake was discovered in 1992 near the Vostok station. After opening the glacial shell at a depth of 3758 m, it was found that the temperature at the ice–water boundary was −2.4°C, and the data of [10] were used in simulating the distribution of density over the lake’s depth [11].

CURVE OF MAXIMUM DENSITY ON WATER ISOBARS

A great many experimental and theoretical studies have been devoted to investigating the properties of water in the normal and supercooled state, which were presented on, e.g., Chaplin’s website [12] and in [12–15].

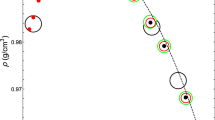
In addition to the phase transformation curves, the p–T diagrams of substances contain a number of other curves that reflect the details of the behavior of a substance, e.g., the line of the unit compressibility factor \({{pV} \mathord{\left/ {\vphantom {{pV} {\left( {RT} \right)}}} \right. \kern-0em} {\left( {RT} \right)}} = 1\), where R is the gas constant; the Joule–Thomson inversion line \({{\left( {{{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial p}}} \right. \kern-0em} {\partial p}}} \right)}_{h}} = 0\), where h is enthalpy; and others. When analyzing experimental data on compressibility, and in deriving the equation of state, the curve of density maxima on isobars \(p{{\left( T \right)}_{{\max d}}}\) (TMD, temperature maximum density), and thus the right boundary of zero CTE values of \({{\alpha }_{p}}\left( {p,T} \right) = 0\), has in recent years often been considered for dense water (particularly in the supercooled state). We can see that the density maximum on the 1 atm isobar is preceded by a minimum at a temperature of <210 K in the amorphous state [16]. The curve of these minima on different isobars p(T)min d forms the left boundary of the zero CTE values. Details of this TMD dependence require further research.

To plot the \(p{{\left( T \right)}_{{\max d}}}\) curve in the phase diagram of water in the temperature range of −5 to 5°С (Fig. 1), and to find its positions relative to the ice melting curve pmelt(T) and the isochore fragments with minima at zero CTE values, we used the data in [10, 17] for the curve of \(p{{\left( T \right)}_{{\max d}}}\), and the results in [18] for the melting curve. These sources also contain information on specific volumes of water, the values of which were used in constructing isochores. We can see (Fig. 1) that the curve of density maxima crosses the melting curve at p ~ 25 MPa; at higher pressures, it moves into the region of supercooled water. In the considered region, the isochores pass through a minimum as the temperature falls and then change the slope from positive to negative (see also [19]), generating nonconventional hydrodynamics in particular [20]. Below the curve of density maxima in the region of negative CTE values, the entropy grows along the isotherm with increasing pressure, passes through a maximum, and then begins to fall in the \({{\alpha }_{p}} > 0\) region of positive CTE values. To illustrate, the change in entropy with increasing pressure for water along the 0°C isotherm is shown below [21] (here, the entropy reference point is the triple point of water):

p, MPa

1

5

10

15

20

25

30

35

40

S, J/(kg K)

−0.1

0.1

0.3

0.4

0.5

0.4

0.3

0.1

−0.2

Fig. 1.
figure 1

Melting line of ice pmelt (fine curve); line of density maxima along isobars pmax d (bold curve); and density isochors (dashed curve), including sections with a negative slope; \({{\left( {{{\partial p} \mathord{\left/ {\vphantom {{\partial p} {\partial T}}} \right. \kern-0em} {\partial T}}} \right)}_{V}} < 0\).

Full size image

This example for water demonstrates the process of escape from the “entropy plus” state domain with increasing parameters. The problem of determining the substances and states for which we can observe the process of entering the region of negative temperature coefficients, accompanied by an increase in the entropy along the isotherm, is a subject of further research. Here we return to Bridgman’s original formulation of “… the drop in entropy caused by the application of any pressure cannot be greater than the total entropy of the body.” A reference value of the entropy of liquid water at 1 atm, measured from 0 K, S0 (273.16 K) = 63.356 J/(mol K) [22], can serve as a guide: the drop in entropy with increasing pressure along the isotherm should not exceed this value.

If the average CTE value of 0.5α (1 atm, 293 K) ~ 2 × 10−4 1/K is taken as a rough estimate of the change in entropy with increasing pressure along the isotherm, the pressure estimate of 10–15 GPa corresponds to a negative pressure decrement ΔS that is close in absolute value to the entropy of water in the standard state. This means that to overcome the entropy crisis at these or lower pressures in water, some structural transformations must occur that lead to an increase in entropy. The article “Anomalies in the Shock and Isentropic Compressibilities of Water” was published in 1983 [23]. Its authors considered possible causes of irregular behavior (kinks) in the shock adiabatic curve of water. They concluded that this anomaly was associated with a structural transition in water in the regions of 1500–2000 K and 5–10 GPa that was accompanied by the emergence of negative thermodynamic coefficient (∂T/∂p)s in the isentropic curve. The region of high pressures with negative coefficients in water in [23] and the same region estimated in this work coincide. Oddly enough, in new works on the equation of state of water at high pressures, this feature finds no quantitative expression even if it is noted [24].

A considerable number of studies have been performed on the shock compression of molecular gases, particularly hydrogen and nitrogen. In a relatively new work on liquid nitrogen [25], there was a notable change in the slope in shock adiabatic curve in T–p coordinates at pressures of 60–70 GPa and temperatures of (10–12) × 103 K, similar to the ones noted for water in [23]. When analyzing this type of experimental data for nitrogen, we consider the possibility of a polymer phase with negative CTE and Grüneisen values forming at high parameters [26]. The details of the phase diagram of nitrogen with the boundaries of entry and exit from the polymer phase and its emergence at higher p, T parameters have been discussed in different works.

In recent decades, there has been a renaissance in studies of solids with negative CTE values. Metal oxide systems, zeolites, and polymers have been discovered whose CTEs at normal pressure over a wide temperature range are negative or change sign during a phase transition. A unique member of this class of substances is ZrW2O8, which has a bulk negative CTE in the range of 3–1100 K [27]. These experimental works have been accompanied by theoretical calculations of the structure and properties of objects from first principles. For example, Liu et al. [28], in considering the microstructure of solids, investigated the correlations of the rise in entropy along an isobar with negative CTE values. However, the thermodynamic behavior of these systems under pressure remains poorly studied.

In the author’s opinion, the observed states of substances with negative thermodynamic coefficients are anomalies only conditionally. They are in fact transitional regions or crossovers between regular states, and can be repeated when the substance is compressed along the isotherms (as we observe in the example of water). Zero values of thermodynamic coefficients (particularly CTE) are merely the boundaries of these transitional regions.