INTRODUCTION

Aluminum alloys that are characterized by perfect physical and mechanical properties are widely used in various fields of industry. However, in manufacturing aluminum casts, issues related to reducing defects in a material and increasing its strength are topical. One of the ways of approaching the problems is the structural refinement of solidified metal by adding nanosized refractory particles to the melt. In accordance with the sizes of particles, their shape, and surface wettability, heterogeneous nucleation at the particles is possible. As the modifiers, preliminarily prepared TiN, TiC, etc., particles are used, which favor the increase in the number of nuclei when the content of the particles in the melt is no more than 0.1 wt % [1–4].

Currently, there are many works related to the study of modification of aluminum melts with refractory particles in the literature. The decrease in the average grain size in casts and improvement of strength properties of solidified metal were confirmed experimentally [1–4]. Attempts to perform a mathematical description of heterogeneous nucleation processes have been made for a long time [5–16]; however, these models are not yet widely applied in studying the solidification.

At the same time, in [17], a model was suggested that combines the population dynamics approach and cellular automata method in order to study the formation of microstructure in modified aluminum alloys. The model describes the kinetics of dissolution of inoculated particles, nucleation, and subsequent crystal growth. Results of the numerical simulation are compared with data obtained experimentally in studying the solidification of an Al–Cu alloy modified with nanosized TiC particles. However, not all results agree with conventional theory and practice. The authors studied the solidification at low contents of particles of 0.05 to 1.2 wt %. At the same time, experimental results indicate that, at a particle content in the melt of more than 0.1%, the coagulation of particles takes place, and the required modification effect is not reached [18].

A mathematical model of solidification of a metal modified with refractory nanosized particles was considered in [19, 20] and heterogeneous nucleation and solidification processes of binary aluminum-based alloys, which are characterized by a eutectic phase diagram, are described. Based on the results of numerical simulation, peculiarities of the kinetics of heterogeneous nucleation and solidification of the melt in a cylindrical crucible are described. The adequate coincidence between the numerical calculation results and experimental data takes place. The nucleation process is considered in assuming that nanosized particles are in the form of a cube with plain faces. However, it is obvious that, after preliminarily treatment, particles have a complex shape, and their surface can be only partially plain. Therefore, it is useful to consider the possibility of heterogeneous nucleation at spherical particles that often are used in models employed by different investigators [8, 11–16]. This will allow us to improve the knowledge about heterogeneous nucleation processes, in particular, in using new information obtained in the course of experiments.

In this study, processes, which occur upon solidification of two-component Al–1% Cu aluminum alloy in an iron crucible, are considered. The melt is modified with refractory nanosized spherical particles clad by aluminum. Basic data of the task are determined from experimental conditions and obtained results available in the literature [17]. A mathematical model, which describes thermodynamic phenomena in the melt and crucible and the heterogeneous nucleation and solidification of α and β components of the binary melt, is formulated. The connection between the value of supercooling and size of nuclei formed at the nanosized particle surface is determined. In performing the numerical simulation, the growth kinetics of solid in the solidified melt is determined. The conformity of the model of solidification in the presence of ultrafine spherical particles in the aluminum alloy is confirmed by the adequate coincidence between calculated and available experimental data.

MATHEMATICAL MODEL AND IMPLEMENTATION ALGORITHM

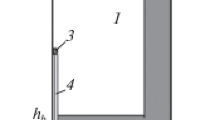
Using experimental data described in [17], the solidification of Al–Cu aluminum alloy in a cast iron cylindrical crucible is considered. The ingot height is H and its radius is Rin; the thickness of crucible bottom and wall is hb and hw, respectively (scheme in Fig. 1). The melt is modified with refractory nanosized spherical particles with radius Rp that is substantially lower than H and Rin; their weight content mp is 0.05%. Heat exchange between the outer surfaces of the crucible, free surface of the melt, and the environment takes place. The thermal resistance Rh at the melt–crucible contact surface, which was determined by experiments [21], is taken into account. A thermocouple measured the temperature is located at the central part of the melt. Thermalphysic parameters of liquid and solid metal are constant and equal to average values for the considered temperature ranges.

Fig. 1.
figure 1

Schematic section of (1) cylindrical crucible with the (2) melt and (3) temperature measuring points.

Full size image

Taking into account the accepted assumptions, the heat transfer is described by equation in cylindrical coordinate system (r, z):

$$\begin{gathered} {{c}_{e}}{{\rho }_{e}}\frac{{\partial T}}{{\partial t}} = \frac{1}{r}\frac{\partial }{{\partial r}}r{{\lambda }_{e}}\frac{{\partial T}}{{\partial r}} + \frac{\partial }{{\partial z}}{{\lambda }_{e}}\frac{{\partial T}}{{\partial z}} + {{\rho }_{2}}{{\kappa }_{0}}\frac{{\partial {{f}_{{\text{s}}}}}}{{\partial t}}; \\ 0 \leqslant r \leqslant {{R}_{{{\text{in}}}}},\,\,\,{{h}_{{\text{b}}}} \leqslant z \leqslant {{h}_{{\text{b}}}} + H, \\ \end{gathered} $$
(1)

where local values of coefficients are ce = c1, ρe = ρ1, λe = λ1 at fs = 0, ce = c2, ρe = ρ2, λe = λ2 at fs = 1, and ce = c1(1 – fs) + c2fs, ρe = ρ1(1 – fs) + ρ2fs, λe = λ1(1 – fs) + λ2fs in the case 0 < fs < 1. Here fs is the volume fraction of solid in the melt; λ, c, and ρ are the thermal conduction, heat capacity, and density, respectively; κ0 is the specific melting heat; i = 1 and i = 2 are the indices at physical parameters for the liquid and solid phases of alloy material, respectively; for crucible material, i = 3.

The temperature change in the crucible is described by the expression

$${{c}_{3}}{{\rho }_{3}}\frac{{\partial T}}{{\partial t}} = {{\lambda }_{3}}\left( {\frac{1}{r}\frac{\partial }{{\partial r}}r\frac{{\partial T}}{{\partial r}} + \frac{{{{\partial }^{2}}T}}{{\partial {{z}^{2}}}}} \right).$$
(2)

The symmetry conditions in the melt and crucible are

$$r({{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial r}}} \right. \kern-0em} {\partial r}}) = 0,\,\,\,\,r = 0,\,\,\,\,~0 \leqslant z \leqslant {{h}_{{\text{b}}}} + H.$$

The condition of heat transfer between the free surface of the melt and the environment is

$${{\lambda }_{e}}({{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial z}}} \right. \kern-0em} {\partial z}}) = {{\alpha }_{1}}({{T}_{{\text{c}}}} - T),\,\,\,0 \leqslant r \leqslant {{R}_{{{\text{in}}}}},\,\,\,z = {{h}_{{\text{b}}}} + H;$$

boundary conditions at the crucible side surface are

$$\begin{gathered} {{\lambda }_{3}}({{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial r}}} \right. \kern-0em} {\partial r}}) = {{\alpha }_{2}}({{T}_{{\text{c}}}} - T), \\ r = {{R}_{{{\text{in}}}}} + {{h}_{{\text{w}}}},\,\,\,0 \leqslant z \leqslant {{h}_{{\text{b}}}} + H, \\ \end{gathered} $$

boundary conditions at the crucible bottom are

$$\begin{gathered} {{\lambda }_{3}}({{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial z}}} \right. \kern-0em} {\partial z}}) = {{\alpha }_{2}}(T - {{T}_{{\text{c}}}}), \\ 0 \leqslant r \leqslant {{R}_{{{\text{in}}}}} + {{h}_{{\text{w}}}},\,\,\,~z = 0, \\ \end{gathered} $$

boundary conditions at the top surface of side wall are

$$\begin{gathered} {{\lambda }_{3}}({{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial z}}} \right. \kern-0em} {\partial z}}) = {{\alpha }_{2}}({{T}_{{\text{c}}}} - T), \\ {{R}_{{{\text{in}}}}} \leqslant r \leqslant {{R}_{{{\text{in}}}}} + {{h}_{{\text{w}}}},\,\,\,\,z = {{h}_{{\text{b}}}} + H, \\ \end{gathered} $$

where α1, α2 are the heat transfer coefficients and Tc is the ambient temperature.

Conditions at the contact surfaces between the metal and crucible are

$$\begin{gathered} {{\lambda }_{e}}{{\left. {({{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial r}}} \right. \kern-0em} {\partial r}})} \right|}_{{{{R}_{{{\text{in}}}}} - }}} = {{\lambda }_{3}}{{\left. {({{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial r}}} \right. \kern-0em} {\partial r}})} \right|}_{{{{R}_{{{\text{in}}}}} + }}} \\ = \,\,{{\left( {{{{\left. T \right|}}_{{{{R}_{{{\text{in}}}}} + }}} - {{{\left. T \right|}}_{{{{R}_{{{\text{in}}}}} - }}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\left. T \right|}}_{{{{R}_{{{\text{in}}}}} + }}} - {{{\left. T \right|}}_{{{{R}_{{{\text{in}}}}} - }}}} \right)} {{{R}_{h}}}}} \right. \kern-0em} {{{R}_{h}}}}, \\ r = {{R}_{{{\text{in}}}}},\,\,\,\,{{h}_{{\text{b}}}} \leqslant z \leqslant {{h}_{{\text{b}}}} + H, \\ {{\lambda }_{e}}{{\left. {({{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial z}}} \right. \kern-0em} {\partial z}})} \right|}_{{{{h}_{{\text{b}}}} + }}} = {{\lambda }_{3}}{{\left. {({{\partial T} \mathord{\left/ {\vphantom {{\partial T} {\partial z}}} \right. \kern-0em} {\partial z}})} \right|}_{{{{h}_{{\text{b}}}} - }}} \\ = \,\,{{\left( {{{{\left. T \right|}}_{{{{h}_{{\text{b}}}} + }}} - {{{\left. T \right|}}_{{{{h}_{{\text{b}}}} - }}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{{\left. T \right|}}_{{{{h}_{{\text{b}}}} + }}} - {{{\left. T \right|}}_{{{{h}_{{\text{b}}}} - }}}} \right)} {{{R}_{h}}}}} \right. \kern-0em} {{{R}_{h}}}}, \\ 0 \leqslant r \leqslant {{R}_{{{\text{in}}}}},\,\,\,\,z = {{h}_{{\text{b}}}}. \\ \end{gathered} $$

The initial temperature (t = 0) in the melt and crucible is

$$T = {{T}_{0}}.$$

The considered melt contains refractory nanosized particles clad with aluminum. In the course of solidification of such a melt, crystals nucleate at the particle surface since, in this case, the consumed energy is less than that upon homogeneous nucleation [11, 15]. We assume that a nucleus can be formed at the wettable surface of a nanosized spherical particle. The nucleus surface contacting with the melt also is assumed to be the surface of a part of sphere. A nucleus can be both smaller and greater than a particle. Figure 2 demonstrates the arrangement of crystal nuclei at the surface of spherical substrate.

Fig. 2.
figure 2

Schemes of crystal nucleation at the particle surface at (a) Rp > Rs and (b) Rp < Rs: (1) liquid; (2) nucleus; and (3) particle.

Full size image

Let us to consider the formation of a crystalline phase nucleus at a solid spherical particle present in the supercooled melt. Let Rp be the particle radius with the center at point 0; Rs is the nucleus radius with the center at point \(0{\kern 1pt} '\) at the particle surface; θ is the interfacial angle at spherical substrate (particle) at point B; and σ12, σ13, and σ23 are the surface tensions at the liquid–nucleus, liquid–substrate, and nucleus–substrate interfaces, respectively. In this case, in accordance with the Gibbs equation [12, 13], the free energy change of system upon formation of equilibrium nucleus is determined by the expression

$$\begin{gathered} \Delta G = - \frac{{{{\kappa }_{0}}{{\rho }_{1}}\Delta T}}{{{{T}_{{l0}}}}}{{V}_{2}} + {{\sigma }_{{12}}}{{S}_{{12}}} \\ + \,\,({{\sigma }_{{23}}} - {{\sigma }_{{13}}}){{S}_{{23}}} + \tau (2\pi {{R}_{{\text{p}}}}\sin \gamma ), \\ \end{gathered} $$

where V2 is the nucleus volume; S12 is the liquid–nucleus interface area; and S23 is the nucleus–substrate interface area. 2πRpsinγ is the contact line length and τ is the linear surface tension energy at the interface between liquid, nucleus, and particle. The AB radius of contact line is determined by expression Rpsinγ, where the value of γ follows from

$$\begin{gathered} {\text{tan}}\gamma = {{{{R}_{{\text{s}}}}\sin \theta } \mathord{\left/ {\vphantom {{{{R}_{{\text{s}}}}\sin \theta } {({{R}_{{\text{p}}}} - {{R}_{{\text{s}}}}\cos \theta )}}} \right. \kern-0em} {({{R}_{{\text{p}}}} - {{R}_{{\text{s}}}}\cos \theta )}},\,\,\,\,{{R}_{{\text{p}}}} > {{R}_{{\text{s}}}}, \\ {\text{tan}}\gamma = {{ - {{R}_{{\text{s}}}}\sin \theta } \mathord{\left/ {\vphantom {{ - {{R}_{{\text{s}}}}\sin \theta } {({{R}_{{\text{p}}}} - {{R}_{{\text{s}}}}\cos \theta )}}} \right. \kern-0em} {({{R}_{{\text{p}}}} - {{R}_{{\text{s}}}}\cos \theta )}},\,\,\,\,{{R}_{{\text{p}}}} < {{R}_{{\text{s}}}}, \\ \end{gathered} $$

Tl0 is the initial liquidus temperature of alloy; ΔT = Tl – T is the supercooling; and Tl is the current liquidus temperature.

The equilibrium condition along the tangent to the particle surface at point B with allowance for the effect of linear tension of wetted perimeter [11, 13]

$${{\sigma }_{{13}}} - {{\sigma }_{{23}}} = {{\sigma }_{{12}}}\cos \theta + {{\sigma }_{\tau }}\cos \gamma ,$$
(3)

where \({{\sigma }_{\tau }} = {\tau \mathord{\left/ {\vphantom {\tau {({{R}_{{\text{p}}}}\sin \gamma )}}} \right. \kern-0em} {({{R}_{{\text{p}}}}\sin \gamma )}}\) is the linear tension of the three-phase contact line. As a result, Eq. (3) is written as

$${{\sigma }_{{13}}} - {{\sigma }_{{23}}} = {{\sigma }_{{12}}}\cos \theta + {\tau \mathord{\left/ {\vphantom {\tau {({{R}_{{\text{p}}}}{\text{tan}}\gamma )}}} \right. \kern-0em} {({{R}_{{\text{p}}}}{\text{tan}}\gamma )}}.$$

The surface tension linear energy is described by the relationship

$$\tau = \frac{{{{a}_{0}}}}{{\sin \theta }}{{\sigma }_{{12}}}(1 + \cos \theta )[2\cos \theta - \sqrt {2(1 + \cos \theta )} ],$$
(4)

where a0 is the radius of molecular action sphere. It follows from Eq. (4) that τ < 0 at 0° < θ < 180°.

We take into account that \({{\sigma }_{{12}}} = \sigma _{{12}}^{\infty }(1 - {{2\delta } \mathord{\left/ {\vphantom {{2\delta } {{{R}_{{\text{s}}}}}}} \right. \kern-0em} {{{R}_{{\text{s}}}}}}),\) δ is the Tolman parameter [22], and \(\sigma _{{12}}^{\infty }\) is the surface tension at the plain nucleus–aluminum melt interface. Then, using the expression

$$\begin{gathered} \Delta G = - \frac{{{{\kappa }_{0}}{{\rho }_{1}}\Delta T}}{{{{T}_{{{\text{l}}0}}}}}{{V}_{2}} + {{\sigma }_{{12}}}({{S}_{{12}}} - {{S}_{{23}}}\cos \theta ) \\ + \,\,\tau \left( {2\pi {{R}_{{\text{p}}}}\sin \gamma - \frac{{{{S}_{{23}}}\cos \gamma }}{{{{R}_{{\text{p}}}}\sin \gamma }}} \right), \\ \end{gathered} $$
(5)

which describes the free energy change of system upon formation of a nucleus, the critical nucleus size R* and critical Gibbs energy ΔG* for different supercoolings ΔT can be calculated. When the condition \(\tau [2\pi {{R}_{{\text{p}}}}\sin \gamma - {{{{S}_{{23}}}\cos \gamma } \mathord{\left/ {\vphantom {{{{S}_{{23}}}\cos \gamma } {({{R}_{{\text{p}}}}\sin \gamma )}}} \right. \kern-0em} {({{R}_{{\text{p}}}}\sin \gamma )}}] < 0\) is satisfied, the lower energy is consumed for the appearance of a nucleus of critical size.

According to [7], the rate of nucleation of α-component crystals (Al) is determined by the expression

$$I = K\exp \left\{ { - \frac{{\Delta G{\text{*}}}}{{{{k}_{{\text{B}}}}T}}} \right\},$$
(6)

where kB is the Boltzman constant; K is the kinetic parameter that generally depends on the surface tension, modifying particle size, and number of atoms at the particle surface; and T is the temperature (K).

According to [7], the expression for kinetic parameter K in Eq. (6) is written in the form

$$K = {{n}_{{\text{s}}}}\frac{{{{k}_{{\text{B}}}}T}}{h}\exp \{ {{ - E} \mathord{\left/ {\vphantom {{ - E} {({{k}_{{\text{B}}}}T)}}} \right. \kern-0em} {({{k}_{{\text{B}}}}T)}}\} ,$$

where \({{n}_{{\text{s}}}} = {{n}_{{\text{p}}}}\left( {{{4\pi R_{{\text{p}}}^{2}} \mathord{\left/ {\vphantom {{4\pi R_{{\text{p}}}^{2}} {l_{{\text{a}}}^{2}}}} \right. \kern-0em} {l_{{\text{a}}}^{2}}}} \right)\) is the number of metal atoms contacting with the nanosized particle surface; \({{n}_{{\text{p}}}}\) = \({{{{m}_{{\text{p}}}}{{\rho }_{1}}} \mathord{\left/ {\vphantom {{{{m}_{{\text{p}}}}{{\rho }_{1}}} {\left[ {100{{\rho }_{{\text{p}}}}\left( {{{4\pi R_{{\text{p}}}^{3}} \mathord{\left/ {\vphantom {{4\pi R_{{\text{p}}}^{3}} 3}} \right. \kern-0em} 3}} \right)} \right]}}} \right. \kern-0em} {\left[ {100{{\rho }_{{\text{p}}}}\left( {{{4\pi R_{{\text{p}}}^{3}} \mathord{\left/ {\vphantom {{4\pi R_{{\text{p}}}^{3}} 3}} \right. \kern-0em} 3}} \right)} \right]}}\) is the number of nanosized particles per unit melt volume; ρp is the density of particle substance; la, is the interatomic spacing in the melt; h is the Planck constant; and E is the activation energy of diffusion in the melt.

The number of α-component crystals formed upon supercooling of liquid metal after time tl0, when the temperature reaches Tl0, is

$$N(r,z,t) = \int\limits_{{{t}_{{l0}}}}^t {I(r,z,\zeta )[1 - {{f}_{{\text{s}}}}(r,z,\zeta )]d\zeta } ,$$

where fs is the volume fraction of growing solid, which is described similarly to [23]

$$\begin{gathered} {{f}_{{\text{s}}}}\left( {r,z,t} \right) = 1-{\text{exp}}\left\{ {-N{{V}_{{\text{s}}}}} \right\}, \\ {{V}_{{\text{s}}}}(r,z,t) = ({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3})\left( {{{R}^{3}} - R_{{\text{p}}}^{3}} \right), \\ \end{gathered} $$

Vs is the volume of solid formed at a nanosized particle. It is assumed that the growth of crystalline phase obeys the normal mechanism, and the radius R of its boundary is determined by linear dependence of the growth rate on the supercooling \({{\partial R} \mathord{\left/ {\vphantom {{\partial R} {\partial t}}} \right. \kern-0em} {\partial t}} = {{K}_{\alpha }}\Delta T\) [6]; \(R(r,z,t) = {{R}_{p}} + \int_{{{t}_{{l0}}}}^t {{{K}_{\alpha }}\Delta Td\zeta } ,\) where Kα is a physical constant.

To estimate the kinetic constant Kα, the following formula can be used

$${{K}_{\alpha }} = {{(D\Delta {{H}_{{\text{a}}}})} \mathord{\left/ {\vphantom {{(D\Delta {{H}_{{\text{a}}}})} {\left( {{{l}_{{\text{a}}}}{{k}_{{\text{B}}}}T_{A}^{2}} \right)}}} \right. \kern-0em} {\left( {{{l}_{{\text{a}}}}{{k}_{{\text{B}}}}T_{A}^{2}} \right)}},$$

where ∆Ha is the enthalpy of melting per atom; the coefficient of diffusion D in liquid is determined by the Arrhenius equation \(D = {{D}_{0}}\exp \{ {{ - E} \mathord{\left/ {\vphantom {{ - E} {({{k}_{{\text{B}}}}T)}}} \right. \kern-0em} {({{k}_{{\text{B}}}}T)}}\} \) [24].

The expression for the determination of supercooling ΔT = Tl – T is written in the form

$$\Delta T = {{T}_{A}} - {{\beta {{C}_{0}}} \mathord{\left/ {\vphantom {{\beta {{C}_{0}}} {{{{(1 - {{f}_{{\text{s}}}})}}^{{1 - k}}}}}} \right. \kern-0em} {{{{(1 - {{f}_{{\text{s}}}})}}^{{1 - k}}}}} - T.$$

Here, the liquidus temperature Tl is related to the dissolved component (Cu) concentration С; TA is the melting temperature of pure metal solvent (Al); and β is the modulus of liquidus slope in the Al–Cu phase diagram. The alloying component concentration is determined by nonequilibrium state lever equation (Scheil equation) C = C0/(1 – fs)1 – k [6, 25], where С0 is the initial concentration and k is the dissolve-component distribution coefficient. The growth of solid α component (aluminum) of the alloy occurs in a temperature range Tl0 ≥ T ≥ TE, where Tl0 = TA – βC0 and TE is the eutectic temperature.

The calculation of the α component crystallization by Eq. (1) is performed using the specific melting heat of aluminum κAl as the κ0 parameter. It is assumed that at T = TE, the fraction of solid is fsα.

After cooling of the metal to the eutectic temperature, the solidification of the β component of alloy occurs. The formation of α-component crystal nuclei does not occur and N = N(r,z,tE). Because of the low mutual solubility of aluminum and copper, it is assumed that, during subsequent cooling of the melt, the growth of solid obeys the normal mechanism that is characterized by growth constant Kβ. The radius R of the boundary of solid phase that grows around a particle after time t = tE, when the melt temperature reaches TE, is

$$\begin{gathered} R(r,z,t) = {{R}_{\alpha }} + \int\limits_{{{t}_{{\text{E}}}}}^t {{{K}_{\beta }}({{T}_{{\text{E}}}} - T)d\zeta } , \\ {{R}_{\alpha }}(r,z,{{t}_{{\text{E}}}}) = {{R}_{p}} + \int\limits_{{{t}_{{l0}}}}^{{{t}_{E}}} {{{K}_{\alpha }}\Delta Td\zeta } , \\ \end{gathered} $$

whereas the volume Vsβ of β-component that forms to time moment t is

$${{V}_{{{\text{s}}\beta }}}(r,z,t) = ({{4\pi } \mathord{\left/ {\vphantom {{4\pi } 3}} \right. \kern-0em} 3})\left( {{{R}^{3}} - R_{\alpha }^{3}} \right).$$

The fraction of solid fsβ in solidified eutectic melt is determined by the expression

$${{f}_{{{\text{s}}\beta }}} = 1-\exp \{ -N{{V}_{{{\text{s}}\beta }}}\} .$$

In calculating the eutectic solidification by Eq. (1), the specific melting heat of copper κCu is used instead of the κ0 parameter. The eutectic solidification occurs in the temperature range TE > T ≥ Tend, where Tend is the temperature corresponding to the complete solidification of the melt. The fraction of solid fs in the course of solidification is determined by expression

$${{f}_{{\text{s}}}} = {{f}_{{{\text{s}}\alpha }}} + {{f}_{{{\text{s}}\beta }}}.$$

To implement the model, the finite difference algorithm is used. The calculation region was divided into I × J cells. Spatial grid steps (Δr, Δz) were selected so that the melt–crucible interface is arranged equidistantly between neighboring mesh points located in the melt and crucible. Along the temporary variable, the uniform grid with the step Δt was used. Difference equations were constructed via the approximation of balanced relationships obtained by integration of Eqs. (1) and (2) using corresponding boundary conditions. The approximation order is \(O\left( {{{\Delta }_{t}},\Delta _{r}^{2},\Delta _{z}^{2}} \right).\) The temperature distribution was described by values at grid nodes. The algebraic system obtained by implicit approximation of heat transfer equations was solved by iteration method [26]. Calculations were performed until the solidification of the melt is complete. The adequacy of the model and its implementation algorithm are confirmed by qualitative and quantitative coincidence between the calculated data and results of physical experiments [17].

RESULTS OF CALCULATIONS

The numerical study of the dynamics of solidification of the modified melt was performed for the following crucible and Al–1% Cu alloy parameters [17, 19, 21, 27]: Rin = 0.01 m, H = 0.04 m, hb = 0.01 m, hw = 0.01 m, с1 = 1050 J/(kg K), λ1 = 100 W/(m K), ρ1 = 2.35 × 103 kg/m3, с2 = 1150 J/(kg K), λ2 = 220 W/(m K), ρ2 = 2.57 × 103 kg/m3, κAl = 3.89 × 105 J/kg, κCu = 2.1 × 105 J/kg, T0 = 993 K, TA = 933 K, Tl0 = 929.15 K, TE = 821 K, β =3.85 K/%, C0 = 1 wt %, k = 0.14, a0 = 0.143 × 10–9 m, Kα = 7 × 10–5 m/(s K), Kβ = 7 × 10–5 m/(s K); for modifying particles TiC: ρp = 4930 kg/m3, mp = 0.05 wt %, Rp = 91 × 10–9 m; la = 2.86 × 10–10 m, lc = 4.33 × 10–10 m, D0 = 10–7 m2/s, ∆Ha = 1.75 × 10–20 J, E = 4.2 × 10–20 J, \(\sigma _{{12}}^{\infty }\) = 0.093 J/m2, kB = 1.38 × 10‒23 J/K, θ = 5°, δ = 2.98 × 10–10 m, с3 = 540 J/(kg К), λ3 = 45 W/(m К), ρ3 = 7.3 × 103 kg/m3; Rh = 10‒4 m2 K/W, α1 = 150 W/(m2 K); α2 = 150 W/(m2 K), Tc = 293 K. In the course of experiments, the thermocouple measuring the temperature is placed in the center of ingot (r = 0, z = hb + H/2) [17].

Figure 3a illustrates the Gibbs energy change ΔG described by Eq. (5) at different supercoolings of the melt. It follows from calculated results that, at a supercooling of 0.5 K, the conditions for the nucleation of steady nucleus, the size of which is comparable with the particle size, are absent. At a supercooling of 1 K, the radius of spherical nucleus formed at the particle surface can reach the critical size R*, which is corresponding to the maximum free energy (Gibbs energy) ΔG*. The values of critical radii correspond to points in the axis Rs at which the ΔG function takes the maximum values. In particular, at ΔT = 1 K, R* = 189 nm, ΔG* = 7.4 × 10–15 J and, at ΔT = 1.5 K, R* = 126 nm, ΔG* = 1.2 × 10–15 J. Thus, at low supercoolings, the critical radii of formed nuclei are higher than the modifying nanosized particle radius Rp = 91 nm (Fig. 3а).

Fig. 3.
figure 3

Gibbs energy change ΔG upon nucleation at ΔT equal to (1) 0.5, (2) 1, (3) 1.5, (4) 2.5, (5) 3, and (6) 3.5 K: (а) Rs > Rp and (b) Rs < Rp.

Full size image

Since the interfacial angle used at the spherical particle is constant, θ = 5°, the nuclei having the critical size R* ≈ Rp do not appear. At a supercooling more than 2.3 K, the conditions for the formation of nuclei, the critical radii of which are less than the modifying particle radius Rp, appear (Fig. 3b). In particular, at ΔT = 2.5 K, R* = 75 nm, ΔG* = 5.6 × 10–19 J; at ΔT = 3 K, R* = 61 nm, ΔG* = 8.2 × 10–20 J; and, at ΔT = 3.5 K, R* = 50 nm, ΔG* = 1.6 × 10–20 J.

It is necessary to note that, as the supercooling increases in order to form nuclei having critical sizes, the consumed energy is substantially lower. Namely, according to Eq. (6), the value of energy ΔG* has a decisive influence on the possibility of formation of nuclei.

To test the solidification model, the volume solidification of the Al–1% Cu alloy with inoculated refractory TiC particles in the cylindrical crucible is considered. In performing the calculations, in order to determine starting and boundary conditions, we use the experiment, in which the metal temperature was measured during solidification of a cylindrical ingot 0.02 m in diameter and 40 mm in height [17]. Figure 4 illustrates the temperature change and fraction of solid in the solidified metal in the center of formed ingot (r = 0, z = hb + H/2) and at the contact point with the lateral surface of crucible (r = R, z = hb + H/2). Figure 4a shows calculated results that qualitatively and quantitatively coincide with results of the physical experiment and indicate that the suggested model adequately describes the temperature change in the center of ingot during solidification of the modified alloy.

Fig. 4.
figure 4

(a) Temperature change and (b) fraction of solid in the melt (1) near the side wall of crucible and (2) in the center of ingot. Symbols and solid lines correspond to experimental and calculated data, respectively.

Full size image

At the contact point of the metal with the side wall of crucible, the overheating is removed in 1.09 s and, after that, the supercooling of the melt below the liquidus temperature by 2.52 K takes place (Figs. 4a, 5a). At ΔT ≤ 2.3 K, the nucleation is absent. At ΔT > 2.43 K, for 0.01 s, the active nucleation of α-component crystals occurs (Fig. 5a). The appearance and growth of crystalline phase lead to the rapid decrease in the supercooling below 2.43 K, and nucleation stops. Taking into account the fact that nuclei appear at a supercooling more than 2.3 K, their size is less than that of modifying particles. The solidification of the α component of the Al–Cu alloy near the wall continues for 12.65 s, the fraction of solid in the melt increases, and the supercooling decreases (Figs. 4b, 5a). When the melt temperature reaches the eutectic temperature TE and the faction is fsα = 0.98, the eutectic solidification of the β component occurs. The complete solidification ends at 14th s.

Fig. 5.
figure 5

(1) Supercooling and (2) nucleation rate in the melt (a) at the side wall of crucible and (b) in the center of ingots. Dashed line corresponds to ΔT = 2.43 K.

Full size image

The overheating in the center of ingot is completely removed in 2.2 s, and supercooling of the melt starts (Fig. 5b). However, after 1 s, the supercooling stops the increase and, for several seconds, remains equal to 2.43 K. This occurs because of balancing the release intensity of latent-heat of crystallization and intensity of heat removal to the environment. Then, as the supercooling increases, the formation of α component crystal nuclei begins. Taking into account the fact that the supercooling of the melt in the center of ingot exceeds 2.3 K, the nucleus size is less than the modifying particle size. At ΔT ≤ 2.3 K, the nucleation is absent. The active solidification of the α component (Al) begins at 9th s and continues for 1.5–2 s. The eutectic solidification of the β component (Cu) and complete solidification ends to 17th s (Fig. 4b).

The solidification time, supercooling, and solidification rate substantially change as the distance from the side wall of crucible increases (Figs. 4, 5). This results in different conditions of nucleation and start of solidification in the melt. Figure 6a demonstrates the change in the amounts of nuclei formed in the center of ingot and at the contact point of the melt with crucible at z = hb + H/2. The area characterized by the finer structure of the metal is near the side wall of crucible; this qualitatively coincides with the available experimental data [3]. In the center of ingot at r < 0.007 m, after removal the overheating, the nucleation conditions almost do not differ and, therefore, crystals are of equal size. Figure 6b shows average grain sizes calculated by formula d0 = 1/N1/3, which agree with experimental data [17].

Fig. 6.
figure 6

Variations of the (a) number of nuclei and (b) grain size across the cross-section of ingot. Symbols correspond to the average grain size determined experimentally.

Full size image

CONCLUSIONS

The mathematical model for the solidification of the binary (Al–Cu) alloy modified with refractory nanosized spherical particles is suggested. The numerical simulation of the melt solidification in a cylindrical crucible is performed and peculiarities of solidification are considered. The initial parameters of the task were determined from experimental conditions and obtained results available in the literature. The kinetics of heterogeneous nucleation and solidification during cooling of the melt is considered. It was determined that the nucleation and solidification conditions inside the ingot substantially differ. It was found that the critical radii of formed nuclei are less than the modifying nanosized particle radius; nuclei greater than the modifying particles do not appear. The calculated temperature conditions of the alloy solidification and grain sizes of solidified metal agree adequately with available experimental data.