INTRODUCTION

Advances in the growth technology have made it possible to prepare CoFe/Cu superlattices with one of the highest values of the giant magnetoresistive effect (GMR) [1]. A microwave giant magnetoresistive effect (μGMR) of record magnitude has recently been obtained [2] in superlattices of this type. It is known that anomalous values of the refractive index can occur in micro-inhomogeneous media and metamaterials, making it possible to observe several unusual phenomena [3]. Knowing this index allows one to calculate the transformation of fields at the interfaces, and can be useful in calculating microwave devices. The complex refractive index is calculated from the known values of the permittivity and permeability. As shown in [4], the microwave refractive index can change significantly due to strong changes in permeability under conditions of ferromagnetic resonance (FMR). The refractive index also depends on the complex effective permittivity εef = ε' – iε". The conductivity of metallic nanostructures can vary significantly in a magnetic field, and εef changes accordingly. Preliminary experiments carried out in [5] showed that the refractive index changes under the conditions of the μGMR effect.

Microwave methods are successfully used to study metallic nanostructures [6, 7]. It was shown in [8] that changes in the high-frequency transmission coefficient of a nanostructure are practically equal to the relative magnetoresistance. The fact that the giant magnetoresistance affects the coefficient of microwave reflection from the nanostructure is shown in [9]. The microwave properties of Co/Cu nanostructures with high magnetoresistance were studied in [10, 11]. The magnetoresistance of spin valves at microwave frequencies was studied in [12].

The microwave refractive index of CoFe/Cu superlattices is studied in this work to establish the main cause of its change in a magnetic field. The measurements were based on the transmission of microwaves through the nanostructure, which makes it possible to obtain quantitative data on microwave conductivity. The CoFe/Cu system, in which adjacent ferromagnetic layers are coupled by exchange interaction, is convenient for such analysis, since it has a large GMR. In addition, using the transmission method, one can observe ferromagnetic resonance and reconstruct the dependence of the permeability on the external magnetic field. From these measurements, the effective permittivity and permeability were determined, and the complex refractive index and its field dependence were calculated.

EXPERIMENTAL

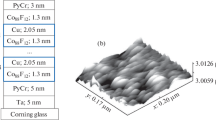
The microwave properties of two [(Co0.88Fe0.12)/Cu]n superlattices with compositions Ta(5)/PyCr(5)/[Co0.88Fe0.12(1.5)/Cu(0.95)]24/Ta(5) (sample no. 1) and Ta(5)/PyCr(5)/[Co0.88Fe0.12(1.3)/Cu(2.05)]8 Co0.88Fe0.12(1.3)/PyCr(3) (sample no. 2) were studied. Here, Py denotes permalloy, PyCr = (Ni80Fe20)60Cr40 is an alloy, and the numbers in parentheses denote the layer thickness in nanometers. The number after the brackets denotes the number of layer pairs in the superlattice. Superlattices were prepared by magnetron sputtering using an MPS-4000-C6 installation on 0.2-mm-thick Corning glass substrates. The thickness of the Cu spacer was chosen so that, for the first sample, the thickness ts = 0.95 nm falls on the first maximum of the magnetoresistance and the thickness of the second sample, ts = 2.05 nm, falls on the second maximum. Structural studies on a DRON_3M diffractometer with CoKα radiation showed that both superlattices have a perfect layer structure with an fcc lattice and an 〈111〉 axial texture with an axis normal to the layer plane. The electrical conductivity of the samples was measured by a DC four-contact method at room temperature. The measured dependence of the conductivity of the samples on the magnetic field is shown in Fig. 1. A magnetic field is applied in the plane of the sample. As can be seen from the figure, changes in the conductivity occur in these samples in different ranges of the magnetic field: H < 10 kOe for the first sample and H < 0.3 kOe for the second sample.

Fig. 1.
figure 1

Conductivity of superlattices vs. magnetic field.

Full size image

Microwave measurements were carried out by the method described in [8], using the transmission and reflection of waves. The sample was placed in the cross section of the waveguide, completely covering it. The magnetic field was applied in the plane of the superlattice, parallel to the narrow side of the waveguide, so that the vectors of constant, H, and variable, H~, magnetic fields be mutually perpendicular, H ⊥ H~. Using a scalar network analyzer at frequencies from 26 to 38 GHz, the absolute value of the transmission coefficient, |D(H)|, and its relative change in a magnetic field, dm = \(\frac{{\left| {D\left( H \right)} \right| - \left| {D\left( 0 \right)} \right|}}{{\left| {D\left( 0 \right)} \right|}},\) as well as the absolute value of the reflection coefficient, |R(H)|, and its relative change in a magnetic field, rm = \(\frac{{\left| {R\left( H \right)} \right| - \left| {R\left( 0 \right)} \right|}}{{\left| {R\left( 0 \right)} \right|}},\) were measured.

RESULTS OF MICROWAVE MEASUREMENTS

The measured dependences of the absolute value of the transmission coefficient are shown in Fig. 2. For sample no. 1, a monotonic decrease in the transmission coefficient is observed, which can be associated with the μGMR effect and explained by a decrease in the skin depth with an increase in the conductivity of the superlattice. The magnetic saturation field is ~7 kOe. In addition to this monotonic change, the dependences exhibit resonant changes caused by the microwave absorption under the FMR conditions. These results are presented for frequencies f = 35 and 38 GHz, at which the resonant changes occur when the sample is close to magnetic saturation. Similar results for sample no. 2 are shown in Fig. 2b. Here, in the given range of magnetic fields, only nonresonant changes caused by the μGMR are seen.

Fig. 2.
figure 2

Microwaves transmission coefficient of superlattices vs. magnetic field: (a) sample no. 1 and (b) sample no. 2.

Full size image

CALCULATION OF THE REFRACTIVE INDEX AND DISCUSSION

To calculate the refractive index, one needs to know the effective permittivty εeff or the conductivity and the effective permeability μeff. To estimate μeff, it suffices to assume that the dependence of the permeability on the frequency and the magnetic field strength has the Lorentzian form [13]. The components of the permeability tensor can be expressed via dynamic magnetic susceptibilities: diagonal, χ, and off-diagonal, χa:

$$\mu = 1 + 4\pi \chi ,\,\,\,\,{{\mu }_{a}} = 4\pi {{\chi }_{a}},$$
(1)

and

$$\begin{gathered} \chi = \chi {\kern 1pt} ' - i\chi {\kern 1pt} '' = \frac{{\gamma M{{\theta }_{{\text{v}}}}}}{\Omega }\left\{ {{{\omega }_{H}}\left[ {\omega _{H}^{2} - \left( {1 - {{\alpha }^{2}}} \right){{\omega }^{2}}} \right]} \right. \\ \left. { - \,\,i\alpha \omega \left[ {\omega _{H}^{2} + \left( {1 + {{\alpha }^{2}}} \right){{\omega }^{2}}} \right]} \right\}, \\ \end{gathered} $$
(2a)
$$\begin{gathered} {{\chi }_{a}} = \chi _{a}^{'} - i\chi _{a}^{''} = \frac{{\gamma M{{\theta }_{{\text{v}}}}\omega }}{\Omega }\left\{ {\left[ {\omega _{H}^{2} - \left( {1 + {{\alpha }^{2}}} \right){{\omega }^{2}}} \right]} \right. \\ \left. { - \,\,i2\alpha \omega {{\omega }_{H}}} \right\}, \\ \end{gathered} $$
(2b)

where \(\gamma = \frac{{g\left| e \right|}}{{2mc}}\) is the gyromagnetic ratio, \(g\) is the spectroscopic splitting factor, ω = 2πf is the angular frequency, \({{\theta }_{{\text{v}}}}\) is the volume fraction of ferromagnetic layers, M is the saturation magnetization of the ferromagnetic layer, \({{\omega }_{H}} = \gamma H,\) Ω = \({{[\omega _{H}^{2} - \left( {1 + {{\alpha }^{2}}} \right){{\omega }^{2}}]}^{2}}\) + \(4{{\alpha }^{2}}{{\omega }^{2}}\omega _{H}^{2},\) and α is the damping factor of the magnetic system in the Landau–Lifshitz–Gilbert equation. The damping parameter α can be approximately estimated from the data of the microwave experiments. To that end, it is necessary to transform the field dependences of the transmission, D, and reflection, R, coefficients to find the fraction of the microwave power dissipated in the sample, \(\Delta (H) = 1 - \left[ {\left| {D(H)} \right| + \left| {R(H)} \right|} \right].\) For sample no. 1, the dependence Δ(H) obtained at a frequency f = 38 GHz is shown in Fig. 3a. The absorption of microwaves under the FMR conditions is expressed as a maximum in the field HFMR ≈ 7.5 kOe. The damping factor can be found as α = ΔH/HFMR, where ΔH is the FMR line width [13]. For sample no. 1, we obtained α ≈ 0.015.

Fig. 3.
figure 3

(a) Changes in dissipation of microwaves in magnetic field and (b) microwave permeability in magnetic field. Sample no. 2, frequency f = 38 GHz.

Full size image

Knowing the factor α, the magnetization M from magnetic measurements, and the volume fraction of ferromagnetic layers, \({{\theta }_{{\text{v}}}},\) we can calculate the components of the magnetic susceptibility and permeability tensors by formulas (2a) and (2b). For the field configuration H ⊥ H~, used here, the role of the effective permeability μeff is played by the following combination of the permeability tensor components [13]:

$${{\mu }_{{{\text{eff}}}}} = \mu - \frac{{\mu _{a}^{2}}}{\mu }.$$
(3)

The calculated field dependence of the real and imaginary parts of the permeability μeff for sample no. 1 is shown in Fig. 3b. The real part of the permeability is an alternating function, and the imaginary part has a maximum.

The effective complex permittivity εeff can be calculated from the conductivity of superlattices, \({{\varepsilon }_{{{\text{eff}}}}} = \varepsilon {\kern 1pt} ' - i\varepsilon {\kern 1pt} ''\) = \(\varepsilon {\kern 1pt} ' - i\frac{{4\pi \sigma }}{\omega },\) known from Fig. 1. For a metallic superlattice, the real part of the permittivity can be neglected. The complex refractive index neff = n' – in" can be calculated from the known dynamic permittivity εeff and permeability μeff:

$${{n}_{{{\text{eff}}}}} = n{\kern 1pt} ' - in{\kern 1pt} '' = \sqrt {{{\varepsilon }_{{{\text{eff}}}}}{{\mu }_{{{\text{eff}}}}}} .$$
(4)

The real part of the complex refractive index, n', represents refraction. The imaginary part of the index, n", represents absorption. The dependences of the real and imaginary parts of the complex refractive index on the magnetic field for sample no. 1, calculated by formula (4) for several frequencies, are shown in Fig. 4a. These dependences have a resonant character. It can be seen that FMR makes the main contribution to the change in the refractive index in this sample. The real part of the refractive index has an alternating dependence. The index is negative because, below the FMR field, the effective permeability is negative. The imaginary part of the refractive index at FMR has a maximum due to absorption of waves. The dependences in Fig. 4a were plotted taking into account the change in the conductivity of the sample shown in Fig. 1. To select the contribution to the refractive index from the GMR, it is necessary to make a calculation with a constant conductivity of the sample, σ = σ(H = 0), and compare the result with the calculation at σ = σ(H).

Fig. 4.
figure 4

Refractive index of superlattices vs. magnetic field: (a) sample no. 1, calculations for several frequencies. Selection of the contribution from the giant magnetoresistance: (b) sample no. 1 and (c) sample no. 2.

Full size image

This was done for the absolute value of the refractive index, |neff|, (Fig. 4b). It can be seen from the figure that FMR makes the main contribution to the change in the refractive index in this sample, but the contribution from the GMR is also present. To select the contribution from the GMR, sample no. 2 is more convenient, because most of the change in conductivity in it occurs in fields below 0.2 kOe, which is much lower than the FMR field. Figure 4c shows the dependence of the absolute value of refractive index on the magnetic field, calculated for fields below 1 kOe. It is clearly seen here that there is a contribution to |neff| from the GMR. The results in Fig. 4c are consistent with previously published results [5].

CONCLUSIONS

In this work, we have considered the dependence of the microwave refractive index on the magnetic field for [(Co0.88Fe0.12)/Cu]n metal superlattices, which have a giant magnetoresistive effect. Measurements of the coefficient of transmission of waves through superlattices at frequencies from 26 to 38 GHz were carried out. It has been found that the dependence of the transmission coefficient on the magnetic field is caused by the ferromagnetic resonance and the giant magnetoresistive effect. From microwave measurements of ferromagnetic resonance, the field dependence of the permeability has been reconstructed. This made it possible to calculate the complex refractive index and its real part. It has been found that there are two contributions to the field dependence of the refractive index: resonant, caused by the FMR, and nonresonant, caused by the GMR. The refractive index in fields lower than the FMR field is negative.