Experimental Study of Image-Forming Lens Based on Diffractive Lenses, Correcting Aberrations

Abstract

The simplest lens, consisting of the refractive and diffractive lenses, in which the main geometric aberrations are compensated due to the shape of the diffractive lens, is considered. It is considered the way of calculation of this system based on minimization of a chromatic aberration. The results of the experiment, in which a frequency–contrast characteristic of a hybrid lens was directly determined, are presented.

INTRODUCTION

Increasingly more complex optics is used in modern smartphones in order to get an image of high-quality. Since, now, the package thickness doesn’t allow getting in these lenses at normal arrangement, the configuration with a rotating prism is used in the last models of smartphones. The minimization of size of the lens is a topical problem, without which solution, a further reduction of sizes of these devices is not possible. Sizes of the lens can be minimized by using diffractive or harmonic lens [1–8]. Chromatism can be reduced due to a particular shape of these lenses, but still a relatively high chromatic aberration of these optical elements must be eliminated by an additional digital processing [9]. On the one hand, an additional processing is well suited for registering devices in modern smartphones, having a high computing power, on the other hand, an optical resolution in modern smartphones is so high, that the digital processing is not sufficient, and it is desirable to use a lens, which is comparable in terms of image quality with lenses of a classical type based on a great number of refractive lenses. The hybrid systems, containing both refractive and diffractive elements, are considered more frequently [10–15]. However, works on hybrid systems are not used all capabilities for correction of aberrations based on diffractive lenses. The diffractive lenses in these systems are classically used either as some achromatizing element in the composition of a classical multiple-lens lens [10] or in combination with a refractive element of a free shape [12], which compensates geometric aberrations in the lens. The essentially bifocal systems are also used [14, 15]. A relief of the diffractive lens to compensate the main geometric aberrations was not attempted to modify in any of works. In this paper, an attempt is made to combine the compensation of chromatic and geometric aberrations in a single diffractive lens.

1. BASIC FORMULAS

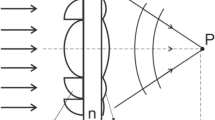
The main idea of using the diffractive optics in the composition of classical imaging lenses is based on the fact that the material dispersion of refractive lenses and dispersion of focusing properties of the diffractive lens have different signs. As the wavelength increases the focal distance of the refractive lens increases; the opposite effect is observed for the diffractive lens. When parameters are correctly chosen, the use of the doublet (Fig. 1) made of the refractive and diffractive lenses allows one to completely exclude the chromatic aberration on two wavelengths and decrease it in the interval between these wavelengths.

Fig. 1.

Classical illustration of the doublet made of the refractive and diffractive lenses, in which, a chromatic aberration is compensated.

This scheme is solely considered as a model principally not suitable for practical use, since when using a standard spherical refractive lens and a standard diffractive lens, approximating a similar spherical lens, a system with significant geometric aberrations is obtained. Therefore, the diffractive optics is considered in the composition of sufficiently complex optical systems [7, 8] only as an element for compensation of chromatic aberration. However, capabilities of the diffractive optics are not restricted only by compensation of chromatic aberrations. A particular attention should be paid to results of work [9], where the most complex refractive element of a free shape was used to compensate chromatic aberrations, and the diffractive lens is also in the optical system. This work illustrates well the approach of researchers, which are very familiar with the calculation of refractive systems and not using all capabilities of the diffractive optics. The diffractive lens can approximate any aspheric surface of an arbitrarily high complexity by arrangement of zones, which allows one to simultaneously use it also as a compensator of geometric aberrations, and the diffractive chromatism practically doesn’t depend on this shape.

We consider the basic computing formulas to form a refractive–diffractive achromatic doublet. The condition of achromatization is the equality of focal distances of the system of two lenses at two wavelengths. The focal distance on wavelength λ₁ for refractive lens will be determined by formula

$$f({{\lambda }_{1}}) = \frac{{{{R}_{1}}{{R}_{2}}n({{\lambda }_{1}})}}{{\left[ {n({{\lambda }_{1}}) - 1} \right]\left[ {n({{\lambda }_{1}})({{R}_{1}} + {{R}_{2}}) - d(n({{\lambda }_{1}}) - 1)} \right]}},$$

(1)

where R₁ is the radius of curvature of the first surface, R₂ is the radius of curvature of the second surface, d is the lens thickness, n(λ₁) is the index of refraction on wavelength λ₁.

The focal distance for diffractive lens will be determined as

$${{f}^{d}}\left( {{{\lambda }_{1}}} \right) = \frac{{{{\lambda }_{0}}{{f}_{0}}}}{{{{\lambda }_{1}}}},$$

(2)

where λ₀ is the calculated wavelength, f₀ is the calculated focal distance. It is similarly for wavelength λ₂

$$f({{\lambda }_{2}}) = \frac{{{{R}_{1}}{{R}_{2}}n({{\lambda }_{2}})}}{{[n({{\lambda }_{2}}) - 1][n({{\lambda }_{2}})({{R}_{1}} + {{R}_{2}}) - d(n({{\lambda }_{2}}) - 1)]}},$$

(3)

$${{f}^{d}}\left( {{{\lambda }_{2}}} \right) = \frac{{{{\lambda }_{0}}{{f}_{0}}}}{{{{\lambda }_{2}}}}.$$

(4)

The total focal distance of the system made of the diffractive and refractive lenses is expressed by formula

$$F = \frac{{f{{f}^{b}}}}{{f + {{f}^{d}} - D}}.$$

(5)

The condition for equality of the total focal distance is

$$\frac{{f({{\lambda }_{1}}){{\lambda }_{0}}{{f}_{0}}}}{{{{\lambda }_{1}}\left[ {f({{\lambda }_{1}}) + \frac{{{{\lambda }_{0}}{{f}_{0}}}}{{{{\lambda }_{1}}}} - D} \right]}} = \frac{{f({{\lambda }_{2}}){{\lambda }_{0}}{{f}_{0}}}}{{{{\lambda }_{2}}\left[ {f({{\lambda }_{2}}) + \frac{{{{\lambda }_{0}}{{f}_{0}}}}{{{{\lambda }_{2}}}} - D} \right]}}.$$

(6)

After simple transformations, we obtain

$${{\lambda }_{0}}{{f}_{0}} = \frac{{f({{\lambda }_{1}})f({{\lambda }_{2}})({{\lambda }_{1}} - {{\lambda }_{2}}) - d[f({{\lambda }_{2}}){{\lambda }_{2}} - f({{\lambda }_{2}}){{\lambda }_{1}}]}}{{f({{\lambda }_{1}}) - f({{\lambda }_{2}})}}.$$

(7)

It is obvious that the best result is achieved if the calculated wavelength will be placed between λ₁ and λ₂, ${{\lambda }_{0}} = \frac{{{{\lambda }_{1}} + {{\lambda }_{2}}}}{2}$, then (7) is transformed to the form

$${{f}_{0}} = \frac{{2\left\{ {f\left( {{{\lambda }_{1}}} \right)f\left( {{{\lambda }_{2}}} \right)\left( {{{\lambda }_{1}} - {{\lambda }_{2}}} \right) - d\left[ {f\left( {{{\lambda }_{2}}} \right){{\lambda }_{2}} - f\left( {{{\lambda }_{1}}} \right){{\lambda }_{1}}} \right]} \right\}}}{{\left( {{{\lambda }_{1}} + {{\lambda }_{2}}} \right)\left[ {f\left( {{{\lambda }_{1}}} \right) - f\left( {{{\lambda }_{2}}} \right)} \right]}}.$$

(8)

The phase function of the diffractive lens was calculated based on a simple condition: a nonideal wavefront ${{\varphi }_{R}}\left( r \right)$ from the beam incident on the system, which is parallel to an optical axis, formed by the refractive lens after passing through the diffractive lens must become an ideal spherical wavefront ${{\varphi }_{0}}\left( r \right)$, converging exactly to the point of intersection of the focal plane of the system with an optical axis. Therefore, the phase function of the lens will be determined by the difference of the phase functions of the formed by the refractive lens and ideal wavefronts

$${{\varphi }^{d}}\left( r \right) = {{\varphi }_{0}}\left( r \right) - {{\varphi }_{R}}\left( r \right),$$

(9)

where r is the distance from the optical axis.

2. SIMULATION

A system with optical parameters corresponding to an average smartphone lens was initially calculated. Figure 2 presents one of possible configurations of lens f = 3.5 mm (equivalent 28 mm at crop factor 8), performed in commercial software ZEMAX. The first lens, typical spherical, with R₁ = 1.9 mm, R₂ = 16.7 mm, 0.5 mm thick (BK7 glass), is mounted, the diffractive lens is placed at distance 0.5 mm from it on the substrate of the same glass and the same thickness. A microrelief of the lens is on a PMMA film with a thickness of 0.81 μm. The diffractive lens is an approximation of the lens obtained from (9).

Fig. 2.

The hybrid system made of the refractive and diffractive lenses with a focal distance of 3.5 mm.

Unfortunately, ZEMAX doesn’t allow us to work with nonstandard diffractive lenses (the standard Fresnel lens is used in Fig. 2), therefore, to calculate the point spread function (PSF) a formed hybrid system, it was developed a special software, which allowed us to determine PSF. Figure 3 presents PSF calculated in this software for a lens on the range of wavelengths from 400 to 700 nm.

Fig. 3.

The point spread function of the hybrid lens with a focal distance of 3.5 mm: the dependence of the intensity of light on a spatial coordinate in the direction, which is perpendicular to the optical axis.

As can be seen from Fig. 3, the width of PSF of the obtained hybrid system is 0.9 μm, which approximately corresponds to the diffraction limit.

3. PREPARATION OF DIFFRACTIVE LENS

The modelled hybrid system is not appropriate for performing experiment due to technical difficulties with implementation of the experimental optical system. The light-sensitive matrices which experimentalists have are significantly larger than matrices used in smartphones. To calculate the experimental system, the refractive lens with exactly known parameters was chosen as a basis: f = 30 mm, lenticular with the same radiuses of curvature, made of BK7 glass. The calculation was performed for the range of wavelengths from 450 to 1000 nm. The wavelength in the middle of this range, that is, 725 nm, was used as a calculated wavelength. Since, the lens was formed on a photoresist with the index of refraction 1.64, the calculated height of the microrelief was 1130 nm. This allowed us to exactly calculate parameters of the wavefront, formed by the lens at a distance of 5 mm from its backward nodal plane, and form the phase function of the diffractive lens based on calculations. Due to the reasons of a technological character, it was decided to implement the phase addition for compensation of the wavefront (9) in the form of an envelope of the diffractive microrelief (Fig. 4). The diffractive lens, which profile is presented in Fig. 4, was prepared by the method of the direct laser writing on a photoresist [16]. The focal distance of the lens was about 1200 mm. Unfortunately, the lens microrelief height close to the center is a bit higher than the calculated one (around 1400 nm), but, starting from radius 1500 µm, coincides with the calculated value with an error not more than 10%. By taking into account the fact that less than 10% of luminous energy passes through the region of radius 1500 µm, this error shouldn’t significantly affect quality of the formed image.

Fig. 4.

Profilogram of the prepared diffractive lens with a focal distance of 1190 mm.

The total focal distance of the system formed by refractive and diffractive lenses was 29.25 mm, which is not very different from the initial focal distance and allows one to further compare the results of operation of a single refractive lens and the developed hybrid s-ystem.

4. EXPERIMENT

To perform experiment, the optical scheme presented in Fig. 5 was assembled.

Fig. 5.

Scheme of the optical setup: (1) LED panel with a uniform brightness, (2) film with a lighting test pattern, (3) refractive lens f = 30 mm, (4) diffractive lens f = 1190 mm, (5) light-sensitive matrix.

The verification of the operation of a hybrid lens was assumed to be in a wide-angle regime, therefore, a test pattern of width 300 mm was placed at a distance of only 800 mm from the lens (field of view around 20°). Figure 6 presents the image of one of test patterns used in experiments. Three striped test patterns with different positions relative to the optical axis of the system were used.

Fig. 6.

Test pattern for experiment with the hybrid lens.

A special software, which calculated an image contrast of stripes of different frequency on the basis of obtained images of test patterns, was developed for experiment.

Figure 7 presents the image of a part of the test pattern and its section in the software, from which the contrast as a function of frequency of lines (frequency–contrast characteristic, FCC) was calculated.

Fig. 7.

(a) the image of a part of the test pattern and (b) section (the dependence of intensity on a spatial coordinate from 0 to 0.95 mm) of this image.

It can be seen from Fig. 7 that the hybrid system operates best in the region near the optical axis (more low-frequency lines on the left have less contrast, than more high-frequency lines in the center).

FCC for the hybrid system and a single refractive lens were obtained based on series of experiments with different test patterns. Figure 8 presents experimental FCC for the hybrid system, frequencies are given per raster of a light-sensitive matrix (width 10 mm, pixel size 4.75 μm).

Fig. 8.

Experimental FCC for hybrid system (frequencies are given per size of the raster of a light-sensitive matrix).

The average value of contrast over series of experiments was 0.17. The average value of contrast for a single refractive lens is 0.14. When narrowing the field of view from 20° to 10°, average values of contract were 0.22 and 0.16, respectively. Therefore, the advantage of this hybrid system over a single refractive lens increases when narrowing the field of view. A set of lines in Fig. 8 on frequency around 90 was formed due to inaccurate experimental determination of frequency in the image (±1–2 pixels).

CONCLUSIONS

The hybrid system in the form of a refractive-diffractive doublet is capable to form PSF, comparable in width with the diffraction limit in a sufficiently wide spectral range, which is confirmed by the simulation data. The performed experiment proves a significant improvement of FCC of the developed system compared to the FCC of a single refractive lens with the same focal distance, which allows us to confirm the simulation data. Further increasing the image quality in this optical system is a purely engineering problem on increasing the accuracy of formation of a microrelief of the diffractive lens.