Geometrooptical Mechanism of Wave-Front Reconstruction

Abstract

Mechanism of wave-front reconstruction based on geometrooptical reflection of reconstructing radiation from the surfaces of constant phase difference between the object and the reference waves used for recording an interference pattern in a recording medium is analyzed. The mechanism is compared with the holographic one. Experimental studies in a bulk recording medium and in a planar optical waveguide are carried out. Several types of achromatic optical elements are proposed. An acousto-optic focusing element capable of inducing strong local stress inside a medium in a region of special shape is discussed. The possibility of reconstruction of temporal structure of light pulses is demonstrated.

INTRODUCTION

The mechanism of wave-front reconstruction by a hologram is based on diffraction of reconstruction radiation from a quasi-periodic structure recorded in the hologram. It is in the local period of this structure that information on the wave-front of the object wave is contained. This mechanism works in both thin and volume holograms recorded in both converging and counterpropagating beams. According to another mechanism proposed in [1], the wave front of the object wave can be reconstructed due to geometrooptical (GO) reflection of reconstruction radiation from a single surface of the holographic-pattern maximum that works similar to a mirror of variable curvature. It is this local curvature that contains information on the object wave front. In contrast to holographic reconstruction, reconstruction radiation experiences no diffraction from a periodic interference structure under GO reconstruction. This makes the process of reconstruction achromatic, i.e., allows reconstructing an unperturbed wave front by light with a wavelength different from that used for recording [2, 3]. The GO mechanism of wave-front reconstruction was proposed for holography. However, it is substantially d-ifferent from the holographic one and is of interest by itself.

In the present work, the GO mechanism of wave-front reconstruction is compared with the holographic one. We explain why this mechanism does not work in ordinary holograms, including the Denisiuk-type holograms. Recording in a bulk recording medium by means of ultrashort laser pulses is used for the GO wave-front reconstruction. In another version, a two-dimensional analog of the effect is obtained in a planar optical waveguide. Several types of achromatic optical and acousto-optic elements and system are proposed. In addition, reconstruction of temporal structure of ultrashort light pulses is discussed.

GO RECONSTRUCTION PRINCIPLES

Let object wave A_O(r)exp[ikL_O(r)] and reference wave A_R(r)exp[ikL_R(r)] obey scalar GO equations ([4], paragraph 1). Here, k = 2π/λ is the wavenumber; λ is the wavelength of radiation; L_O(r) and L_R(r) are the eikonals of the waves; A_O(r) and A_R(r) are their amplitude functions; r is the radius-vector. Intensity of the interference field of these waves is given by

$$A_{O}^{2}({\mathbf{r}}) + A_{R}^{2}({\mathbf{r}}) + 2{{A}_{O}}({\mathbf{r}}){{A}_{R}}({\mathbf{r}})\cos \{ k[{{L}_{R}}({\mathbf{r}}) - {{L}_{O}}({\mathbf{r}})]\} .$$

(1)

Let us analyze the case of a thin hologram first (Fig. 1a). Let the hologram be reconstructed by wave A_R(r)exp[ik'L_R(r)], where wavenumber k' = 2π/λ' can be different from that used for hologram recording. The resulting field obtained as a result of interaction (transmission and reflection) of the reconstruction wave with the hologram can be obtained from (1) in the form of a sum in which the term related to the reconstructed wave front is proportional to [5]

$${{A}_{O}}({\mathbf{r}})A_{R}^{2}\exp \left\{ {i\left[ {\left( {k{\kern 1pt} '\; - k} \right){{L}_{R}}({\mathbf{r}}) + k{{L}_{O}}({\mathbf{r}})} \right]} \right\}.$$

(2)

Fig. 1.

Wave-front reconstruction: (a) by a hologram, (b) by means of the GO mechanism.

Wave (2) is characterized by eikonal

$${{L}_{{{\text{diffr}}}}}({\mathbf{r}}) = (\lambda {\kern 1pt} '{\kern 1pt} {\text{/}}\lambda ){{L}_{O}}({\mathbf{r}}) + (1 - \lambda {\kern 1pt} '{\kern 1pt} {\text{/}}\lambda ){{L}_{R}}({\mathbf{r}}).$$

(3)

Hence, the eikonal of the object wave will be reconstructed only if λ' = λ. For arbitrary λ', expression (3) describes the dependence of shape of the reconstructed wave front on wavelength (dispersion), and leads to the grating equation (section 8.6.1, expression (8) in [6]) in the case of plane waves and to the Meier’s formulas [7] in the case of spherical waves.

Following [1], let us analyze surfaces on which the argument of the cosine function in (1) remains constant (Fig. 1b). For brevity, we will refer to these surfaces as isophase ones, although, strictly speaking, these are the surfaces on which the phase difference of the interfering waves is constant, or the surfaces on which intensity of the resultant field is constant. These surfaces are defined by equation

$${{L}_{R}}({\mathbf{r}}) - {{L}_{O}}({\mathbf{r}}) = p,$$

(4)

where p is constant for each isophase surface. If reconstruction wave A_R(r)exp[ik'L_R(r)] experiences a GO reflection from surface (4), phase k'L_refl(r) of the reflected wave on this surface coincides with the phase of the reconstruction wave [4]:

$$k{\kern 1pt} '{\kern 1pt} {{L}_{{{\text{refl}}}}}({\mathbf{r}}) = k{\kern 1pt} '{\kern 1pt} {{L}_{R}}({\mathbf{r}}).$$

(5)

Relations (4) and (5) yield

$${{L}_{{{\text{refl}}}}}({\mathbf{r}}) = {{L}_{O}}({\mathbf{r}}) + p,$$

(6)

i.e., the object-wave eikonal becomes reconstructed at any value of k' to within an additive constant, in contrast to the case of a thin hologram. It also follows from expression (6) that the wave front of the object wave (surface L_O(r) = const) becomes reconstructed achromatically. Hence, waves reconstructed by means of these two mechanisms do not coincide with each other at λ' ≠ λ.

The following simple examples demonstrate the difference between holographic and GO reconstruction. In a simple case of plane object and reference waves, the holographic mechanism corresponds to diffraction of a plane from a grating, while the GO mechanism corresponds to reflection of the reconstruction wave from a plane mirror. If the object wave is spherical, the corresponding structures are a Fresnel zone plate and a parabolic mirror. In a general case, the GO reconstruction is similar to reflection from a mirror surface of complex curvature.

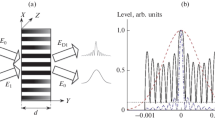
A common volume hologram contains fragments of surfaces on which interference pattern attains maxima. They form a periodic structure containing a large number of such surfaces. As a rule, a volume hologram is recorded in a plane-parallel layer with a thickness varying from several micrometers to several tens of micrometers and a transverse size between several centimeters and several tens of centimeters. Hence, the length of the periodic structure along the surface of the hologram usually by several orders the size of each fragment of the surface of interference maximum inside the layer (Fig. 2a). As a result, the diffraction mechanism of reconstruction dominates the GO one [8, 9], which can be seen from the dependence of the direction of the beam reconstructed by a volume hologram on the wavelength of the reconstruction radiation that can be seen within the range of spectral selectivity of the hologram.

Fig. 2.

Surfaces of interference-pattern maxima: (a) in a common volume hologram, (b) in a structure recorded by ultrashort pulses in a material of increased thickness.

EXPERIMENTAL

In order to obtain a GO reconstruction, the number of maxima of the interference pattern recorded in the volume of the medium must be reduced, while the thickness of the recording medium must be increased. This can be achieved by recording interference of ultrashort laser pulses [10, 11]. The condition of GO mechanism being dominant for a hologram recorded in a plane-parallel layer has the form [9]

$$T\cos \psi \gg D,$$

(7)

where T is the thickness of the plane-parallel layer; ψ is the angle between the grating vector and the normal to the layer surface; D is the width of the recorded interference structure in the direction normal to the isophase planes (Fig. 2b). If the hologram is recorded by two collinear counterpropagating short pulses of equal duration τ, we have D ~ τc, where c is the speed of light in the recording medium. Criterion (7) was obtained in [8, 9] by using the classical Gabor−Stroke approach [12].

A femtosecond titanium-sapphire laser with a pulse width of 40 fs and wavelength tunable between 780 and 830 nm was used in the experiments. The pulse repetition rate was equal to 80 MHz, and the average laser output power was equal to 200 mW. The laser beam was split in two by means of a dielectric beamsplitter, and the beams were directed toward each other. The recording plate was installed in such a way that its photosensitive layer was located in the region of overlap of the counterpropagating pulses. The technique proposed in [13] was used to make the optical path lengths equal. The normal to the plate surface was directed at an angle of 20° with respect to the optical axis. Specially prepared photoplates with a thickness of photosensitive layer varying between 110 and 280 µm were used. The exposure was selected experimentally and was on the order of several tenth of joule per square centimeter. Several fields were illuminated on each photoplate with different exposures. For control, some of the fields were exposed to a continuous-wave radiation in the same geometry as in the case of pulsed radiation. Reconstruction was conducted in the reflection geometry. A dye laser (Rhodamine 6G solution in ethylene glycol) pumped by an argon laser was used for reconstruction. The laser operated in a continuous-wave regime, and its wavelength was tuned from 580 to 630 nm. The reconstructed light beam was observed on a screen installed at a distance of about 4 m from the photoplate. The reconstructed beam could be observed while tuning the laser wavelength from 585 to 607 nm. In the process, the spot formed by the reconstructed beam on the screen did not move. In contrast, the spot formed by the beam reconstructed by the hologram recorded by a continuous-wave radiation under the same conditions was shifting by 6 cm. This result suggests that the reconstruction mechanism in the case of structure recorded by femtosecond pulses is the GO one.

However, large thickness of the recording medium that is required for observation of the effect represents a serious problem hindering its application. Photographic processing of the medium of such large thickness poses obvious technical difficulties. In addition, light absorption in such layers in the course of recording [14] leads to substantial reduction of diffraction efficiency [15, 16]. To overcome these problems, we propose using a waveguide analog of the GO reconstruction. Suppose that the hologram is recorded in a planar waveguide by ultrashort laser pulses that are coupled into the waveguide through its upper boundary (Fig. 3a). Reconstruction takes place in a waveguide regime (Fig. 3b). In this case, the reconstruction regime is two-dimensional. The top view of the waveguide hologram exposed to a reconstruction light beam will be similar to a cross section in the three-dimensional case (Fig. 2b). Therefore, we can use criterion (7) of the GO reconstruction mechanism being dominant if we replace the layer thickness T in it by the width of the reconstructing beam in the waveguide plane. In this case, the thickness of the structure is given by D ~ τc/sin(φ/2), where φ is the angle between the beams recording the hologram. Obviously, the conditions of GO reconstruction are independent of the planar-waveguide thickness in this case. This is the major advantage of the waveguide GO reconstruction over its three-dimensional analog.

Fig. 3.

The GO mechanism in a planar waveguide: (a) recording, (b) reconstruction.

In the experiment, we used a layer of bichrome gelatin (n₂ = 1.54) with a thickness of 20 µm on a polished quartz substrate (n₁ = 1.456) as a model of a planar waveguide. The second harmonic (λ = 400 nm) of the titanium-sapphire laser was used for recording. The laser pulse width was on the order of 30 fs. In the course of recording, pulses were split and were incident on the waveguide sample through its upper surface (Fig. 3a). Angle φ between recording beams was close to 60°. Processing of bichrome gelatin after exposure consisted in washing it in cold water and drying in solutions of isopropyl alcohol of increasing concentration. Reconstruction was performed in the waveguide regime (Fig. 3b). Prisms fabricated from yttrium-aluminum garnet with a base angle of 60° were used for coupling the radiation in and out of the planar waveguide. A dye laser (Rhodamine 6G solution in ethylene glycol) pumped by the second harmonic (λ = 532 nm) of a Nd:YAG laser was used for reconstruction. The wavelength of the reconstruction radiation was varied from 580 to 630 nm. The reconstructed beam coupled out from the waveguide was observed within the range of spectral selectivity of the hologram between 580 and 615 nm. The direction of the reconstructed beam was determined with an accuracy of 6 × 10^–4 rad. It should depend on wavelength in the case of holographic reconstruction. In this case, variation of calculated value of angle α within the range of spectral selectivity of the structure would be on the order of 0.03 rad. The value of angle α measured in the experiment did not change. This fact proves that the GO mechanism is responsible for wave-front reconstruction in this case.

Digital synthesis of a waveguide achromatic hologram containing only a few periods can be used instead of straightforward holographic recording. We propose using the focused ion beam (FIB) nanotechnology for fabrication of waveguide optical elements (OE). The possibility of obtaining a periodic structure with a large aspect ratio by this method was demonstrated in [16]. We used the Strata^TM FIB 201 system with a minimum gallium-beam spot size of 7 nm. Two versions were explored. In the first one, periodic structure was formed directly in the polymer layer. In the second, periodic structure was initially formed on a silicon plate and was later replicated on a polymer by means of ultraviolet solidification. The polymer samples were fabricated by V. I. Sokolov (Institute of the Problems of Laser and Information Technologies, Russian Academy of Sciences, Troitsk, Moscow region, Russia). Periodic structures formed on polymer and silicon are illustrated in Figs. 4a and 4b, respectively. The images were obtained with an FIB system by collecting the signal of secondary electrons. To see the grating profile, a special rectangular void perpendicular to the grooves of the grating was etched in the sample. The images were taken with a sample tilted by 45°. Periodic structures with a grove depth-to-width ratio of about 20 were obtained. The grove width near maximum was about 200 nm.

Fig. 4.

Fabrication of a grating by means of the FIB: (a) in a polymer, (b) in silicon.

Achromatic waveguide OEs can be used for operating ultrashort laser pulses that have broad spectrum. In addition, they can be used for parallel signal processing at different frequencies. Both directions are needed for increasing the speed of information processing. Possible functions of such elements include beam focusing, beam coupling in and out, along with coupling between planar and fiber waveguides.

ACHROMATIC OPTICAL AND ACOUSTO-OPTIC ELEMENTS AND SYSTEMS

Similar to the two-dimensional case, three-dimensional achromatic OEs can be obtained not by means of direct recording but rather by using the methods of digital holography. In the latter case, the shape of an OE is calculated first, and it is synthesized by one way or another after that. Stetson [17] discussed the fundamental possibility of achromatic wave-front reconstruction by a hypothetical isolated isophase surface, provided that it is made infinitely thin and mirror reflective. This popular scientific paper was very important due to studies that it has inspired. Citing Stetson’s paper [17], Sheridon [18] paid attention to the fact that adjacent surfaces of the interference-pattern maxima have a very similar shape. This fact was used for the following experiment. Sheridon recorded a hologram in the reflection geometry in a photoresist. After processing of the latter, its surface attained the shape similar to that of the grating with a sawtooth (blazed) profile. Each groove of this grating represented part of some surface of the interference-pattern maxima. Adjacent grooves belonged to adjacent surfaces of maxima. The height of spike in the grating profile between the groves corresponded to a phase jump of 2π. A computer-synthesized optical element that was similar to the blazed Sheridon hologram [18] was proposed a year later and was named a kinoform [19]. The so-called deep kinoforms also referred to as multiorder or harmonic diffraction lenses in which the phase jump at a zone boundary equals 2πN (where N is an integer) were developed later [20–24]. However, holograms with a sawtooth profile and kinoforms are not achromatic. Obviously, the spikes in the surface relief can correspond to a phase jump of 2π or 2πN only for radiation of a certain wavelength. To make an OE achromatic, phase jumps must be eliminated. An OE that reconstructs a wave front achromatically must be optically equivalent to one of the surfaces of the interference-pattern maxima, so that the wave exhibiting such a wave front would interfere with a certain reference wave. The shape of this surface must be calculated or measured experimentally. A synthesized OE can be either reflective or transmissive. The shape of surface of a reflective optical element in the simplest case coincides with the shape of the surface of the interference-pattern maxima. Upon switching from a reflective OE to its transmissive equivalent, coordinate of each point on the OE surface along its optical axis must be multiplied by 2/(n – 1) (where n is the refractive index of the material from which the transmissive OE is fabricated). The technology of obtaining an OE exhibiting the surface of required shape depends on that shape, the OE size, and the required precision [3]. If available technology does not allow obtaining the required range of variation of the OE surface relief, one of the approaches described below can be used.

In the first approach, compensation of phase-jump is proposed [3, 25]. An optical system illustrated in Fig. 5a contains a step-like OE (SE) and an OE with a blazed relief (BE) that are located close to each other. Similar to a kinoform [22], the BE surface is divided into zones. The height of the relief gradually changes within each zone and experiences a sharp change at the boundary between adjacent zones. However, in contrast to a kinoform, the height of the sharp change in the profile is not related to the radiation wavelength. The working surface of each step of the SE relief represents a flat surface normal to the optical axis. There is a one-to-one correspondence between the steps of the SE and the zones of the BE. They are facing each other and have identical projection on the plane normal to the optical axis. The difference in optical path between adjacent steps of the SE in characterized by the same absolute value as the height of the spike at the boundary of the corresponding zones of the BE but has an opposite sign.

Fig. 5.

(a) An achromatic optical system including an OE with a sawtooth (blazed) profile (BE) and a step-like profile (SE) (1, 2—BE zones; 3, 4—SE steps). (b) Shift of ray projection of the ith BE zone relative to the corresponding SE step.

Let us analyze how the optical system illustrated in Fig. 5a works. We neglect refraction in the optical system (ignore oblique rays). In addition, let us assume that l_i $\ll$ $D_{i}^{2}$/λ for all zones, where l_i is the average distance between the ith zone of BE and the corresponding step of the SE, while D_i is the width of the zone (and the step). Let us analyze the combination of a transmissive BE and a reflective SE first. Radiation propagates through the BE first and acquires some phase shift. The optical path length changes stepwise by a(n₁ – n₀) at the boundary between zones 1 and 2 (Fig. 5a), where a is the amplitude of the change in the relief at the zone boundary, n₁ is the refractive index of the BE material, and n₀ is the refractive index of the medium between the BE and the SE. After that, radiation experiences a reflection from the surface of the SE. Optical path difference between the rays reflected from steps 3 and 4 corresponding to zones 1 and 2 is equal to 2hn₀, where h is the height of step 3. After that, radiation passes through the BE the second time. We assume that the rays that propagated through each zone of the BE will be reflected only by the step of the SE corresponding to this zone, and vice versa. In this case, the total optical path difference between the rays that propagated through the system passing through zones 1 and 2 close to the boundary between them will be equal to 2a(n₁ – n₀) – 2hn₀, and the condition of compensation of the phase jumps mentioned above can be expressed in the form

$$h{{n}_{0}} = a({{n}_{1}}-{{n}_{0}}).$$

(8)

An optical system for which relation (8) is fulfilled is equivalent to an OE with continuous change in relief height. Neglecting dispersion of refractive index, such an optical system can be considered to be achromatic. Note that dispersion of refractive index is much smaller than that caused by diffraction of radiation from the periodic structure of a diffraction OE [20].

Another approach includes a reflective BE and a transmissive SE. In this case, the condition leading to compensation of phase jumps has the form

$$h({{n}_{2}}-{{n}_{0}}) = a{{n}_{0}},$$

(9)

where n₂ is the refractive index of the SE material.

In the third option, both elements of the optical system are transmissive. In this case, the phase-jump compensation condition is given by

$$h({{n}_{2}}-{{n}_{0}}) = a({{n}_{1}}-{{n}_{0}}).$$

(10)

When n₁ = n₂ and h = a, the BE and SE can be fabricated on the opposite sides of one and the same substrate.

So far, we did not analyze oblique rays in the optical system (8)−(10). Let us estimate their contribution. First, let us analyze the case in which both OEs are transmissive. Due to oblique incidence of the rays, part of radiation from a certain BE zone will not reach the corresponding step of the SE. Let us consider this part of radiation as noise. Then, part of radiation reaching the corresponding step will be considered as signal. Let the z axis be directed along the optical axis, and θ be the tilt angle of the rays with respect to the z axis. θ_x and θ_y represent projections of angle θ on the xz and the yz planes, respectively. To obtain a quick estimate of the lower limit of the signal-to-noise ratio (S/N), let us use the model in which all rays from some moving ith zone have the same tilt angle with projections $\theta _{{ix}}^{{\max }}$ and $\theta _{{iy}}^{{\max }}$. Suppose that all zones have a rectangular shape, and the ith zone has dimensions D_ix and D_iy along the corresponding axes. Due to the ray tilt, the ray projection of the ith zone of the BE will be shifted relative to the corresponding step of the SE by Δ_ix and Δ_iy along the corresponding axes (Fig. 5b). The shifted ray projection of the moving ith zone is shown in Fig. 5b by a dashed line, while the corresponding step is shown by a solid line. Shifts Δ_ix and Δ_iy are equal to

$$\begin{gathered} {{\Delta }_{{ix}}} = {{l}_{i}}\tan (\theta _{{ix}}^{{\max }})\sim {{l}_{i}}\theta _{{ix}}^{{\max }}, \\ {{\Delta }_{{iy}}} = {{l}_{i}}\tan (\theta _{{iy}}^{{\max }})\sim {{l}_{i}}\theta _{{iy}}^{{\max }}, \\ \end{gathered} $$

(11)

where l_i is the average distance between the OE surfaces. We replaced tangents by their arguments in (11). In our model, the lower limit of the S/N ratio is proportional to the ratio of areas of the shifted zone projection, the first of which is the area within the step, while the second is the area outside of the corresponding step (Fig. 5b):

$$S{\text{/}}N > \sum\limits_{i = 1}^N {\frac{{({{D}_{{ix}}} - {{\Delta }_{{ix}}})({{D}_{{iy}}} - {{\Delta }_{{iy}}})}}{{{{D}_{{ix}}}{{D}_{{iy}}} - ({{D}_{{ix}}} - {{\Delta }_{{ix}}})({{D}_{{iy}}} - {{\Delta }_{{iy}}})}}} $$

$$\begin{gathered} = \sum\limits_{i = 1}^N {\frac{{({{D}_{{ix}}} - {{l}_{i}}\theta _{{ix}}^{{\max }})({{D}_{{iy}}} - {{l}_{i}}\theta _{{iy}}^{{\max }})}}{{{{D}_{{ix}}}{{D}_{{iy}}} - ({{D}_{{ix}}} - {{l}_{i}}\theta _{{ix}}^{{\max }})({{D}_{{iy}}} - {{l}_{i}}\theta _{{iy}}^{{\max }})}}} \\ \approx \mathop \sum \limits_{i = 1}^N \left( {\frac{{{{D}_{{ix}}}{{D}_{{iy}}}}}{{{{l}_{i}}({{D}_{{ix}}}\theta _{{iy}}^{{\max }} + {{D}_{{iy}}}\theta _{{ix}}^{{\max }})}} - 1} \right) \\ \end{gathered} $$

(12)

$$ > \frac{1}{{l\theta }}\mathop \sum \limits_{i = 1}^N \frac{{{{D}_{{ix}}}{{D}_{{iy}}}}}{{{{D}_{{ix}}} + {{D}_{{iy}}}}} - N,$$

where N is the number of zones, while l and θ are the maximum values of l_i and $\theta _{{ix,y}}^{{\max }}$, respectively. In (12), we omitted terms second order in $\theta _{{ix,y}}^{{\max }}$ assuming the latter to be a small parameter. For the case in which one of the OEs is reflective, l must be increased by a factor of two (proportional to an increase in the optical path length for this case). For some special types of OEs (e.g., axisymmetric ones, etc.), the signal-to-noise ratio can be estimated more accurately.

A different version of an achromatic optical system consisting of two OEs that are not divided into zones was proposed in [3]. The first OE can have strong optical power. We assume that its surface can have deviations from the calculated shape caused by errors of fabrication. These errors are compensated for by the second OE that has a weak optical power. The second OE is fabricated based on the results of the measurements of the wave front formed by the first OE. Fabrication of an OE with a weak optical power is much easier. The option in which the OE exhibiting strong optical power is reflective, while that exhibiting weak optical power is transmissive is preferable, since chromatic aberrations of the system related to dispersion of material of the transmissive OE are expected to be small in this case.

An achromatic OE that belongs to the class of special OEs referred to as focusators was proposed in [26]. According to this option, different zones of the OE focus radiation onto different areas that do not overlap with each other. Each zone of the focusator thus functions as an independent GO OE.

Focusing acousto-optic element illustrated in Fig. 6 [27] operates as follows. A laser pulse is incident on the element surface. A converging acoustic wave is generated as a result of fast light absorption in the surface layer of the acousto-optic element. Patent [27] was based on the experimental results obtained by G.A. Askaryan and co-workers [28, 29]. In the experiments, high-power acoustic pulses were generated on a spherical surface and were focused onto a point. Using high-power laser pulses or pulse trains, along with metalized films exploding under the action of an electric discharge, Askaryan obtained pressure exceeding 10³ atm near acoustic-wave focus. An element with a complex shape of its surface that was calculated by solving the inverse problem for the acoustic-wave focusing into an area of required configuration was proposed in [27]. In this case, using a GO element was crucial since generated acoustic pulse can have only one cycle of oscillation [29], i.e., its spectrum will be very broad. Therefore, diffraction elements cannot be used in this case. The requirements to precision of fabrication of the focusing acousto-optic element are much lower than in optics due to the difference in the wavelengths. Such an element can be fabricated by using, e.g., a CNC machine. This technology was proposed in [27] to be used for slowing down the development of cracks in metal components by creating a zone of plastic deformation in the path of crack development.

Fig. 6.

An acousto-optic focusing element: 1—acousto-optic element, 2—laser pulses, 3—acoustic pulses, 4—the region in which stress is induced.

We believe that this technology can be used in other areas, including surgery on internal organs without making a surgical incision in outer tissues of the body. The method provides a fundamental opportunity of imitating the action of a scalpel or other surgical instruments. There are two options of simulating the movement of surgical instruments inside the body. In the first one, the motion of an acousto-optic focusing element along the patient’s body is used. The element must be brought in contact with the body by means of immersion. In the second, a focusing acousto-optic element is made elongated in the direction of scalpel motion, while the laser beam moves along the element. In addition, we assume that this technology can be used for simulation of the action of a bandage upon stopping internal bleeding.

TIME-DOMAIN RECONSTRUCTION

Other effects take place when ultrashort laser pulses are used not only for hologram recording but also for its reconstruction [30]. Reconstruction of the temporal structure of the pulse is one of them. The following simple example demonstrates how it occurs (Fig. 7). Suppose the duration of the reference pulse is much shorter than that of the object signal. In this case, we can consider the reference pulse as a δ pulse. Let the object signal represents two δ pulses separated by time interval τ. We assume that the hologram is recorded in the reflection geometry. The region of spatiotemporal overlap of the object and reference signals thus represents two planes perpendicular to the direction of wave propagation and separated by distance τc/2, where c is the speed of light. Suppose that another δ pulse incident on the structure from the same side as the reference pulse that was used for hologram recording is used as a reconstruction wave. It will be partially reflected initially from the first plane and then from the second. The obtained signal will represent two δ pulses separated by time interval τ. The temporal structure of the object pulse will thus be reconstructed by means of a simple GO reflection.

Fig. 7.

Time-domain reconstruction of a light pulse.

When using a reconstructing wave conjugate with the reference one, it is possible to obtain the object signal reversed in time. In our case illustrated in Fig. 7 this situation corresponds to the case in which reconstructed δ pulse is incident on the recorded structure from the right-hand side.

Holographic methods of reconstruction of temporal structure of short optical pulses are well known [31, 32]. We believe that we deal with a different mechanism of reconstruction in our example. It is possible that it is close to the mechanism of formation of temporal structure of a light pulse by a Bragg grating [33] with the difference that we operate in the spatiotemporal domain in this case rather than in the spectral domain.

CONCLUSIONS

In this work, the difference between the GO mechanism of wave-front reconstruction and the holographic one was demonstrated. The GO wave-front reconstruction was obtained when using ultrashort laser pulses for recording in a bulk recording medium and in a planar waveguide. Several versions of achromatic OEs and optical systems were proposed. An acousto-optic focusing element capable of inducing large local stresses in a region of specified shape inside the medium was proposed. The possibility of reconstruction of temporal structure of optical pulses by means of GO reflection was demonstrated.