INTRODUCTION

Mixed exciton–photon states in planar semiconductor microcavities with quantum wells in the active layer form a new class of quasi-two-dimensional quasi-particles with unique properties [1–13]. Such states are referred to as “microcavity exciton–polaritons.” They arise because of strong coupling of excitons with eigenmodes of the microcavity electromagnetic radiation. Under conditions of a strong coupling, the exciton and photon modes repulse each other and the upper and lower microcavity polariton modes appear. The nonparabolicity of the lower polariton branch allows for the occurrence of a parametric process, as a result of which two pump polaritons are scattered into signal and idler modes with the energy and momentum conservation. Therefore, polariton–polariton scattering, due to which the exciton–polariton system demonstrates strongly nonlinear properties, has elicited great interest from researchers [6–13]. These nonlinearities have been observed in luminescence spectra of microcavities [14–18] under resonant excitation of the lower polariton branch, being explained as being due to the four-wave mixing or parametric scattering of photoexcited pump polaritons into the signal and idler modes. Experimentally, two mechanisms of nonlinearity creating were identified: polariton parametric scattering [6, 19, 20] and blue shift of the polariton dispersion [2, 5]. Using the pump–probe method, the parametric amplification in a microcavity upon excitation of the lower polariton branch by a picosecond pump pulse incident at an angle of 16.5° was observed for the first time in [8, 9]. After the excitation (with a short delay) of the lower polariton branch by an additional weak normally incident probe pulse, it was revealed that, upon reflection, this pulse was amplified by a factor of more than 70. In this case, the idler mode at an angle of 35° also appeared. The resonance conditions were satisfied for these angles specifically.

The results of the experiments that were performed in [8, 9] were also reproduced in [21] and were modeled in [7] using the polariton–polariton scattering mechanism. Similar processes were observed in [22] using two pumping beams at angles of ±45° and a probe beam at an angle of 0°. The parametric oscillator regime was observed in [9, 14] under continuous excitation of the lower polariton branch by the pump radiation at a “magic” angle of 16° without a probe pulse. Above the threshold intensity, intense beams of the signal and idler modes were observed at angles of 0° and 35°, respectively.

In [20], a strong and unusual dependence of the polarization of light emitted by a microcavity on the pumping polarization was revealed. This dependence was interpreted using the pseudospin model in terms of the quasi-classical formalism in which the parametric scattering is described as a resonant four-wave mixing. In [23–25], bistable transmission of radiation was observed in relation to the pumping intensity under excitation of exciton–polaritons in the microcavity. Note that the process of parametric scattering was observed both under pulse excitation [20, 26] and under continuous excitation [14, 16, 27].

Polariton parametric oscillators and amplifiers were described in a number of works [2, 5, 7, 8, 12, 13, 28]. Exciton–exciton interactions play a key role in strong nonlinearities that are present in polariton systems of a microcavity. The first attempt to control these interactions was to use the concept of dipolaritons [29] by incorporating double asymmetric quantum wells into an electrically biased microcavity. Both direct and indirect excitons couple with the same cavity mode, forming a polariton of a new type with similar properties with respect to the exciton–polariton system. In [30], the dynamics of dipolaritons was theoretically studied taking into account three scattering channels. Aperiodic and periodic regimes of the evolution of pump dipolaritons into signal and idler dipolaritons were obtained. In [31], by combining wide quantum wells in a simple waveguide, formation of dipolar polaritons was observed. The main limitation of the studied polariton systems in comparison with their atomic counterparts for studying strongly correlated phenomena and the physics of many bodies is their relatively weak two-particle interaction compared to chaos. In [32], new opportunities were demonstrated for enhancing such local interactions and nonlinearities by tuning the exciton–polariton dipole moment in electrically biased semiconductor microcavities, including wide quantum wells.

At low optical powers, microcavity exciton–polaritons are bistable due to their strong nonlinearities [24]. The polarization dependence of nonlinearities causes polarization multistability [33, 34], which can be used to create spin storage devices [35], logic gates [36, 37], or switches [38].

Self-trapping of exciton–polariton condensates was theoretically predicted in [39] and experimentally observed in [40]. It is explained by the formation of a new polaron-like state. The trapped state of exciton–polaritons is stabilized due to scattering of excitons in the polariton condensate. In [41], the interaction of exciton–polariton condensates with acoustic phonons in a semiconductor microcavity was analyzed. It was shown that parametric instability in the system leads to the generation of a coherent acoustic wave and additional polariton harmonics.

In [42–46], the properties of an optical parametric oscillator were studied using two identical pump photons on the lower branch of the polariton dispersion law. However, it was shown in [47, 48] that two different pump beams can be converted into two frequency-degenerated photons of the signal and idler modes. The occurrence of two different pump beams yields great opportunities for generating signal and idler beams with predetermined properties. In [49], the dynamics of polaritons was studied theoretically in the case when pumping is performed by two lasers with close frequencies without taking into account decay in the medium. Aperiodic and periodic regimes of conversion of a pair of pump polaritons into signal and idler polaritons were found. It was shown that the introduction of two independent pumps leads to an increase in the number of degrees of freedom of the system.

STATEMENT OF THE PROBLEM AND BASIC EQUATIONS

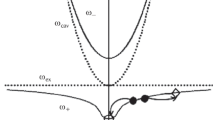
The goal of this work is to study the time variation of the polariton density upon pumping the lower branch at two points of the dispersion law that are close in energy, with taking into account decay. We will assume that the two pump beams differ in amplitude (intensity), but the photon energies differ only slightly. It will be assumed that polaritons are excited on the lower branch of the dispersion law at a magic angle (Fig. 1). It was shown in [4, 5] that the process of parametric scattering of two pump polaritons into signal and idler modes is described by a Hamiltonian of the form

$$\begin{gathered} \frac{1}{\hbar }H = {{\omega }_{{{{p}_{1}}}}}\hat {a}_{{{{p}_{1}}}}^{ + }{{{\hat {a}}}_{{{{p}_{1}}}}} + {{\omega }_{{{{p}_{2}}}}}\hat {a}_{{{{p}_{2}}}}^{ + }{{{\hat {a}}}_{{{{p}_{2}}}}} + {{\omega }_{s}}\hat {a}_{s}^{ + }{{{\hat {a}}}_{s}} \\ + \;{{\omega }_{i}}\hat {a}_{i}^{ + }{{{\hat {a}}}_{i}} + \mu (\hat {a}_{s}^{ + }\hat {a}_{i}^{ + }{{{\hat {a}}}_{{{{p}_{1}}}}}{{{\hat {a}}}_{{{{p}_{2}}}}} + \hat {a}_{{{{p}_{1}}}}^{ + }\hat {a}_{{{{p}_{2}}}}^{ + }{{{\hat {a}}}_{s}}{{{\hat {a}}}_{i}}), \\ \end{gathered} $$
(1)

where \({{\omega }_{{{{p}_{1}}}}}\), \({{\omega }_{{{{p}_{2}}}}}\), \({{\omega }_{s}}\), and \({{\omega }_{i}}\) are the eigenfrequencies of the first and second pump, signal, and idler polaritons, respectively; \({{\hat {a}}_{{{{p}_{1}}}}}\), \({{\hat {a}}_{{{{p}_{2}}}}}\), \({{\hat {a}}_{s}}\), and \({{\hat {a}}_{i}}\) are the polariton annihilation operators; and µ is the constant of parametric polariton–polariton conversion. Using (1), it is easy to obtain a system of Heisenberg equations for operators \({{\hat {a}}_{{{{p}_{1}}}}}\), \({{\hat {a}}_{{{{p}_{2}}}}}\), \({{\hat {a}}_{s}}\), and \({{\hat {a}}_{i}}\). By averaging this system of equations and using the mean-field approximation, the applicability of which was substantiated in [50], we can obtain the following system of nonlinear evolution equations for the complex polariton amplitudes \({{a}_{{{{p}_{1}}}}} = \left\langle {{{{\hat {a}}}_{{{{p}_{1}}}}}} \right\rangle \), \({{a}_{{{{p}_{2}}}}} = \left\langle {{{{\hat {a}}}_{{{{p}_{2}}}}}} \right\rangle \), \({{a}_{s}} = \left\langle {{{{\hat {a}}}_{s}}} \right\rangle \), and \({{a}_{i}} = \left\langle {{{{\hat {a}}}_{i}}} \right\rangle \):

$$i{{\dot {a}}_{{{{p}_{1}}}}} = ({{\omega }_{{{{p}_{1}}}}} - i{{\gamma }_{{{{p}_{1}}}}}){{a}_{{{{p}_{1}}}}} + \mu a_{{{{p}_{2}}}}^{*}{{a}_{s}}{{a}_{i}},$$
$$\begin{gathered} i{{{\dot {a}}}_{{{{p}_{2}}}}} = ({{\omega }_{{{{p}_{2}}}}} - i{{\gamma }_{{{{p}_{2}}}}}){{a}_{{{{p}_{2}}}}} + \mu a_{{{{p}_{1}}}}^{{\text{*}}}{{a}_{s}}{{a}_{i}}, \\ i{{{\dot {a}}}_{s}} = ({{\omega }_{s}} - i{{\gamma }_{s}}){{a}_{s}} + \mu {{a}_{{{{p}_{1}}}}}{{a}_{{{{p}_{2}}}}}a_{i}^{{\text{*}}}, \\ \end{gathered} $$
(2)
$$i{{\dot {a}}_{i}} = \left( {{{\omega }_{i}} - i{{\gamma }_{i}}} \right){{a}_{i}} + \mu {{a}_{{{{p}_{1}}}}}{{a}_{{{{p}_{2}}}}}a_{s}^{*},$$

where \({{\gamma }_{{{{p}_{1}}}}}\), \({{\gamma }_{{{{p}_{2}}}}}\), \({{\gamma }_{s}}\), and \({{\gamma }_{i}}\) are the decay constants of the corresponding polariton states, which we introduce phenomenologically. System of equations (2) will be supplemented by the initial conditions:

$$\begin{gathered} {{a}_{{{{p}_{1}}|t = 0}}} = {{a}_{{{{p}_{1}}0}}}\exp (i{{\varphi }_{{{{p}_{1}}0}}}),\quad {{a}_{{{{p}_{2}}|t = 0}}} = {{a}_{{{{p}_{2}}0}}}\exp (i{{\varphi }_{{{{p}_{2}}0}}}), \\ {{a}_{{s|t = 0}}} = {{a}_{{s0}}}\exp (i{{\varphi }_{{s0}}}),\quad {{a}_{{i|t = 0}}} = {{a}_{{i0}}}\exp (i{{\varphi }_{{i0}}}), \\ \end{gathered} $$
(3)

where \({{a}_{{{{p}_{1}}0}}}\), \({{a}_{{{{p}_{2}}0}}}\), \({{a}_{{s0}}}\), \({{a}_{{i0}}}\), \({{\varphi }_{{{{p}_{1}}0}}}\), \({{\varphi }_{{{{p}_{2}}0}}}\), \({{\varphi }_{{s0}}}\), and \({{\varphi }_{{i0}}}\), are the real amplitudes and phases of polaritons at the initial moment of time.

Fig. 1.
figure 1

Energies of polaritons of the upper and lower branches (ω±). Dispersions of microcavity and exciton eigenfrequencies ωcav and ωex, respectively. Two pump polaritons are scattered into the signal and idler modes.

Full size image

Then, we introduce polariton densities \({{n}_{p}}_{1} = a{{_{p}^{*}}_{1}}{{a}_{{{{p}_{1}}}}}\), \({{n}_{p}}_{2} = a{{_{p}^{*}}_{2}}{{a}_{{{{p}_{2}}}}}\), \({{n}_{s}} = a_{s}^{*}{{a}_{s}}\), and \({{n}_{i}} = a_{i}^{*}{{a}_{i}}\) and two “polarization” components \(Q = i({{a}_{p}}_{1}{{a}_{p}}_{2}a_{s}^{*}a_{i}^{*}\) – \({{a}_{s}}{{a}_{i}}a{{_{p}^{*}}_{1}}a_{{{{p}_{2}}}}^{*})\) and \(R = {{a}_{p}}_{1}{{a}_{p}}_{2}a_{s}^{*}a_{i}^{*}\) + \({{a}_{s}}{{a}_{i}}a{{_{p}^{*}}_{1}}a_{{{{p}_{2}}}}^{*}\).

Using (2), we arrive at the following system of nonlinear differential equations for the introduced functions:

$${{\dot {n}}_{{{{p}_{1}}}}} = - 2{{\gamma }_{{{{p}_{1}}}}}{{n}_{{{{p}_{1}}}}} + \mu Q,\quad {{\dot {n}}_{{{{p}_{2}}}}} = - 2{{\gamma }_{{{{p}_{2}}}}}{{n}_{{{{p}_{2}}}}} + \mu Q,$$
$$\begin{gathered} {{{\dot {n}}}_{s}} = - 2{{\gamma }_{s}}{{n}_{s}} - \mu Q,\quad {{{\dot {n}}}_{i}} = - 2{{\gamma }_{i}}{{n}_{i}} - \mu Q, \\ \dot {Q} = \Delta R + 2\mu ({{n}_{s}}{{n}_{i}}({{n}_{{{{p}_{2}}}}} + {{n}_{{{{p}_{1}}}}}) - {{n}_{{{{p}_{1}}}}}{{n}_{{{{p}_{2}}}}}({{n}_{i}} + {{n}_{s}})) - \Gamma Q, \\ \end{gathered} $$
(4)
$$\dot {R} = - \Delta Q - \Gamma R,$$

where \(\Delta = {{\omega }_{{{{p}_{1}}}}} + {{\omega }_{{{{p}_{2}}}}} - {{\omega }_{s}} - \omega {}_{i}\) is the resonance detuning, \(\Gamma = {{\gamma }_{{{{p}_{1}}}}}\) + \({{\gamma }_{{{{p}_{2}}}}} + {{\gamma }_{s}} + \gamma {}_{i}\). Using (3), the initial conditions for these functions can be written as

$${{n}_{{{{p}_{1}}|t = 0}}} \equiv {{n}_{{{{p}_{1}}0}}} = {{\left| {{{a}_{{{{p}_{1}}0}}}} \right|}^{2}},\quad {{n}_{{{{p}_{2}}|t = 0}}} \equiv {{n}_{{{{p}_{2}}0}}} = {{\left| {{{a}_{{{{p}_{2}}0}}}} \right|}^{2}},$$
$$\begin{gathered} {{n}_{{s|t = 0}}} \equiv {{n}_{{s0}}} = {{\left| {{{a}_{{s0}}}} \right|}^{2}},\quad {{n}_{{i|t = 0}}} \equiv {{n}_{{i0}}} = {{\left| {{{a}_{{i0}}}} \right|}^{2}}, \\ {{Q}_{{|t = 0}}} \equiv {{Q}_{0}} = 2\sqrt {{{n}_{{{{p}_{1}}0}}}{{n}_{{{{p}_{2}}0}}}{{n}_{{s0}}}{{n}_{{i0}}}} \sin {{\theta }_{0}}, \\ \end{gathered} $$
(5)
$${{R}_{{|t = 0}}} \equiv {{R}_{0}} = 2\sqrt {{{n}_{{{{p}_{1}}0}}}{{n}_{{{{p}_{2}}0}}}{{n}_{{s0}}}{{n}_{{i0}}}} \cos {{\theta }_{0}},$$

where \({{\theta }_{0}} = {{\varphi }_{{s0}}} + {{\varphi }_{{i0}}} - {{\varphi }_{{{{p}_{1}}0}}} - {{\varphi }_{{{{p}_{2}}0}}}\) is the initial phase difference.

It is hardly possible to obtain exact analytical solutions of system of equations (4) in the general form. However, if we consider the case of exact resonance (\(\Delta = 0\)) and assume that the decay constants are equal (\({{\gamma }_{{{{p}_{1}}}}} = {{\gamma }_{{{{p}_{2}}}}} = {{\gamma }_{s}} = {{\gamma }_{i}} \equiv \gamma \)), such solutions can be obtained. To do this, we need to introduce new functions:

$${{n}_{{{{p}_{1}}}}} = {{N}_{{{{p}_{1}}}}}\exp \left( { - 2\gamma t} \right),\quad {{n}_{{{{p}_{2}}}}} = {{N}_{{{{p}_{2}}}}}\exp \left( {2\gamma t} \right),$$
$${{n}_{s}} = {{N}_{s}}\exp \left( { - 2\gamma t} \right),\quad {{n}_{i}} = {{N}_{i}}\exp \left( { - 2\gamma t} \right),$$
$$Q = q\exp \left( { - 4\gamma t} \right),\quad R = r\exp \left( { - 4\gamma t} \right),$$

and new variable

$$\xi = \frac{{1 - \exp \left( { - 2\gamma t} \right)}}{{2\gamma }}.$$

Then, system of equations (4) can be reduced to the form

$$\frac{{d{{N}_{{{{p}_{1}}}}}}}{{d\xi }} = \frac{{d{{N}_{{{{p}_{2}}}}}}}{{d\xi }} = \mu q,\quad \frac{{d{{N}_{s}}}}{{d\xi }} = \frac{{d{{N}_{i}}}}{{d\xi }} = - \mu q,$$
$$\frac{{dq}}{{d\xi }} = 2\mu \left( {{{N}_{s}}{{N}_{i}}\left( {{{N}_{{{{p}_{2}}}}} + {{N}_{{{{p}_{1}}}}}} \right) - {{N}_{{{{p}_{1}}}}}{{N}_{{{{p}_{2}}}}}\left( {{{N}_{i}} + {{N}_{s}}} \right)} \right),$$
(6)
$$\frac{{dr}}{{d\xi }} = 0.$$

If variable ξ is assumed to be time, system of equations (6) can be considered to be “conservative,” with solutions being easily found.

From (6), the following integrals of motion can be easily obtained:

$${{N}_{{{{p}_{1}}}}} - {{N}_{{{{p}_{2}}}}} = {{N}_{{{{p}_{1}}0}}} - {{N}_{{{{p}_{2}}0}}},\quad {{N}_{s}} - {{N}_{i}} = {{N}_{{s0}}} - {{N}_{{i0}}},$$
$${{N}_{{{{p}_{1}}}}} + {{N}_{s}} = {{N}_{{{{p}_{1}}0}}} + {{N}_{{s0}}},\quad {{N}_{{{{p}_{2}}}}} + {{N}_{i}} = {{N}_{{{{p}_{2}}0}}} + {{N}_{{i0}}},$$
(7)
$${{q}^{2}} + {{r}^{2}} = 4{{N}_{{{{p}_{1}}}}}{{N}_{{{{p}_{2}}}}}{{N}_{i}}{{N}_{s}},\quad r = {{r}_{0}}.$$

Then, system of equations (4) can be reduced to a single nonlinear differential equation for the density of pump polaritons of the first pulse \({{N}_{{{{p}_{1}}}}}\)

$$\frac{1}{2}{{\left( {\frac{{d{{N}_{{{{p}_{1}}}}}}}{{d\xi }}} \right)}^{2}} + W({{N}_{{{{p}_{1}}}}}) = {{E}_{0}},$$
(8)

where

$$\begin{gathered} W({{N}_{{{{p}_{1}}}}}) = - 2{{N}_{{{{p}_{1}}}}}({{N}_{{{{p}_{1}}}}} - {{n}_{{{{p}_{1}}0}}} + {{n}_{{{{p}_{2}}0}}}) \\ \times \;({{n}_{{{{p}_{1}}0}}} + {{n}_{{s0}}} - {{N}_{{{{p}_{1}}}}})({{n}_{{{{p}_{1}}0}}} + {{n}_{{i0}}} - {{N}_{{{{p}_{1}}}}}), \\ {{E}_{0}} = - {{n}_{{{{p}_{1}}0}}}{{n}_{{{{p}_{2}}0}}}{{n}_{{s0}}}{{n}_{{i0}}}{{\cos }^{2}}{{\theta }_{0}}. \\ \end{gathered} $$
(9)

Here, Eq. (8) represents the law of conservation of energy for a nonlinear oscillator, while the terms in the left-hand sides of (9) play the roles of kinetic and potential energies, respectively, and E0 plays the role of the total energy of the oscillator. The oscillator can oscillate in the range of \({{N}_{{{{p}_{1}}}}}\) in which \(W({{N}_{{{{p}_{1}}}}}) \leqslant {{E}_{0}}\). Qualitatively, the behavior of the function \({{N}_{{{{p}_{1}}}}}\left( \xi \right)\) can be determined by studying the behavior of the potential energy W in relation to \({{N}_{{{{p}_{1}}}}}\) for different values of the parameters. The form of the solution is substantially determined by the roots of the quartic algebraic equation \(W({{N}_{{{{p}_{1}}}}}) = {{E}_{0}}\), which depend on the values of the parameters \({{n}_{{{{p}_{1}}0}}}\), \({{n}_{{{{p}_{2}}0}}}\), \({{n}_{{s0}}}\), \({{n}_{{i0}}}\), and \({{\theta }_{0}}\).

Let us initially consider the case in which the initial phase difference is π/2. Let the initial density of pump polaritons of the second pulse be greater than the initial density of pump polaritons of the first pump pulse (\({{n}_{{p{{0}_{2}}}}} > {{n}_{{p{{0}_{1}}}}}\)) and the initial density of polaritons of the signal mode be higher than the initial density of polaritons of the idler mode (\({{n}_{{s0}}} > {{n}_{{i0}}}\)). The solution of Eq. (8) will then be written as

$$n_{{{{p}_{1}}}}^{{}} = {{n}_{{{{p}_{1}}0}}}\exp ( - 2\gamma t)\frac{{({{n}_{{p{{0}_{1}}}}} - {{n}_{{p{{0}_{2}}}}})({{n}_{{p{{0}_{1}}}}} + {{n}_{{i0}}})}}{{{{n}_{{p{{0}_{2}}}}} - {{n}_{{p{{0}_{1}}}}}{\text{s}}{{{\text{n}}}^{2}}( \pm s + F({{\varphi }_{0}},k))}},$$
(10)

where \(\operatorname{sn} (x)\) is the Jacobi elliptic function with modulus k [51, 52], while quantities k, φ0, and s are expressed by the formulas

$${{k}^{2}} = \frac{{({{n}_{{p{{0}_{2}}}}} + {{n}_{{s0}}})({{n}_{{p{{0}_{1}}}}} + {{n}_{{i0}}})}}{{({{n}_{{p{{0}_{1}}}}} + {{n}_{{s0}}})({{n}_{{p{{0}_{2}}}}} + {{n}_{{i0}}})}},$$
$${{\varphi }_{0}} = \arcsin \sqrt {\frac{{({{n}_{{p{{0}_{2}}}}} + {{n}_{{i0}}}){{n}_{{p{{0}_{1}}}}}}}{{({{n}_{{p{{0}_{1}}}}} + {{n}_{{i0}}}){{n}_{{p{{0}_{2}}}}}}}} ,$$
(11)
$$s = \sqrt {({{n}_{{p{{0}_{1}}}}} + {{n}_{{s0}}})({{n}_{{p{{0}_{2}}}}} + {{n}_{{i0}}})} \mu \frac{{1 - \exp \left( { - 2\gamma t} \right)}}{{2\gamma }}.$$

Now, let us consider the evolution of the system in the case in which, at the initial instant of time, the initial density of pump polaritons of the first pulse is higher than the initial density of pump polaritons of the second pump pulse (\({{n}_{{p{{0}_{1}}}}} > {{n}_{{p{{0}_{2}}}}}\)) and, for definiteness, \({{n}_{{s0}}} < {{n}_{{i0}}}\). Then the solution of Eq. (8) is obtained in the form

$$\begin{gathered} n_{{{{p}_{1}}}}^{{}} = {{n}_{{{{p}_{1}}0}}}\exp ( - 2\gamma t) \\ \times \;\frac{{({{n}_{{p{{0}_{1}}}}} - {{n}_{{p{{0}_{2}}}}})({{n}_{{p{{0}_{1}}}}} + {{n}_{{i0}}})}}{{{{n}_{{p{{0}_{1}}}}} - {{n}_{{p{{0}_{2}}}}} - ({{n}_{{p{{0}_{2}}}}} + {{n}_{{i0}}}){{{\operatorname{sn} }}^{2}}( \pm d + F({{\varphi }_{0}},k))}}, \\ \end{gathered} $$
(12)

where quantities k, φ0, and d are expressed by the formulas

$${{k}^{2}} = \frac{{({{n}_{{p{{0}_{1}}}}} + {{n}_{{s0}}})({{n}_{{p{{0}_{2}}}}} + {{n}_{{i0}}})}}{{({{n}_{{p{{0}_{2}}}}} + {{n}_{{s0}}})({{n}_{{p{{0}_{1}}}}} + {{n}_{{i0}}})}},$$
$${{\varphi }_{0}} = \arcsin \sqrt {\frac{{({{n}_{{p{{0}_{1}}}}} + {{n}_{{i0}}}){{n}_{{p{{0}_{2}}}}}}}{{({{n}_{{p{{0}_{2}}}}} + {{n}_{{i0}}}){{n}_{{p{{0}_{1}}}}}}}} ,$$
(13)
$$d = \sqrt {({{n}_{{p{{0}_{2}}}}} + {{n}_{{s0}}})({{n}_{{p{{0}_{1}}}}} + {{n}_{{i0}}})} \mu \frac{{1 - \exp ( - 2\gamma t)}}{{2\gamma }}.$$

Figures 2a and 2b show that, in both cases, the density of pump polaritons of the first pulse decreases with time, oscillating. The envelopes of the maxima and minima of oscillations decrease exponentially with time. In this case, the spacing between two neighboring peaks (or minima) increases with time. At large values of γ, a decrease in the polariton density at the initial stage of the evolution is characterized by a number of oscillations that is bounded from above, after which an exponential decrease in the density without oscillations is established. This is determined by the fact that, at long times, the argument of the elliptic sine tends to a constant value, the elliptic sine ceases to oscillate in time, and the time evolution of the polariton density is determined in this case only by the exponential factor \(\exp \left( { - 2\gamma t} \right)\).

Fig. 2.
figure 2

Time evolution of density of pump polaritons of the first pulse \(y = \frac{{{{n}_{{{{p}_{1}}}}}}}{{{{n}_{{{{p}_{1}}0}}}}}\) at the initial phase difference θ0 = π/2, as well as at fixed initial densities of pump polaritons of the second pulse, initial polariton densities of the signal and idler modes and decay coefficients: (а) \({{{{n}_{{{{p}_{2}}0}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{p}_{2}}0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 1.5\), \({{{{n}_{{s0}}}} \mathord{\left/ {\vphantom {{{{n}_{{s0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.3\), \({{{{n}_{{i0}}}} \mathord{\left/ {\vphantom {{{{n}_{{i0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.1\), and γ = (1) 0.01, (2) 0.03, and (3) 0.05; (b) \({{{{n}_{{{{p}_{2}}0}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{p}_{2}}0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.6\), \({{{{n}_{{s0}}}} \mathord{\left/ {\vphantom {{{{n}_{{s0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.3\), \({{{{n}_{{i0}}}} \mathord{\left/ {\vphantom {{{{n}_{{i0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.5\), and γ = (1) 0.01, (2) 0.03, and (3) 0.05; (c) \({{{{n}_{{{{p}_{2}}0}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{p}_{2}}0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 1\), \({{{{n}_{{s0}}}} \mathord{\left/ {\vphantom {{{{n}_{{s0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.6\), \({{{{n}_{{i0}}}} \mathord{\left/ {\vphantom {{{{n}_{{i0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.3\), and \(\gamma = 0.01\); (d) \({{{{n}_{{{{p}_{2}}0}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{p}_{2}}0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 1\), \({{{{n}_{{s0}}}} \mathord{\left/ {\vphantom {{{{n}_{{s0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.6\), \({{{{n}_{{i0}}}} \mathord{\left/ {\vphantom {{{{n}_{{i0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.6\), and \(\gamma = 0.01\). Here, \(\tau = {{\mu t} \mathord{\left/ {\vphantom {{\mu t} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}}\).

Full size image

Finally, if the initial density of pump polaritons of the first pulse is equal to the initial density of pump polaritons of the second pulse (\({{n}_{{p{{0}_{1}}}}} = {{n}_{{p{{0}_{2}}}}}\)), then the solution of Eq. (8) is obtained in the form

$$\begin{gathered} n_{{{{p}_{1}}}}^{{}} = {{n}_{{{{p}_{1}}0}}}\exp ( - 2\gamma t) \\ \times \;\frac{{4ab}}{{C\exp ( \pm z) + 2(a + b) + \frac{{{{{(a - b)}}^{2}}}}{C}\exp ( \mp z)}}, \\ \end{gathered} $$
(14)

where

$$a = {{n}_{{p{{0}_{1}}}}} + {{n}_{{s0}}},\quad b = {{n}_{{p{{0}_{1}}}}} + {{n}_{{i0}}},$$
$$C = \frac{{\sqrt {{{n}_{{i0}}}({{n}_{{p{{0}_{1}}}}} + {{n}_{{s0}}}) + {{n}_{{s0}}}({{n}_{{p{{0}_{1}}}}} + {{n}_{{i0}}})} }}{{{{n}_{{p{{0}_{1}}}}}}},$$
$$z = 2\mu \sqrt {ab} \frac{{1 - \exp \left( { - 2\gamma t} \right)}}{{2\gamma }},$$

which, if the initial polariton densities of the signal and idler modes are equal (\({{n}_{{s0}}} = {{n}_{{i0}}}\)), yields

$$n_{{{{p}_{1}}}}^{{}} = \frac{{{{n}_{{p{{0}_{1}}}}}({{n}_{{p{{0}_{1}}}}} + {{n}_{{s0}}})\exp \left( { \pm 2\mu ({{n}_{{p{{0}_{1}}}}} + {{n}_{{s0}}})\frac{{1 - \exp ( - 2\gamma t)}}{{2\gamma }}} \right)}}{{{{n}_{{s0}}} + {{n}_{{p{{0}_{1}}}}}\exp \left( { \pm 2\mu ({{n}_{{p{{0}_{1}}}}} + {{n}_{{s0}}})\frac{{1 - \exp ( - 2\gamma t)}}{{2\gamma }}} \right)}}\exp ( - 2\gamma t).$$
(15)

It follows from (14) and Fig. 2c that the solution with the plus sign monotonically decreases with time, while the solution with the minus sign initially grows to attain a maximum at some point in time, and then monotonically decreases. At long times, the two solutions behave themselves identically. The solutions with the plus and minus signs differ from each other only in the value of a constant phase, which is determined by the initial particle densities and by the two initial, equal in size, but opposite in direction, initial rates of change of the function \({{n}_{{{{p}_{1}}}}}(t)\). Qualitatively, the different behavior of these solutions at short times is explained by the fact that, in the first case, the density of pump polaritons of the first pulse decreases both because of decay and due to an aperiodic conversion of pump polaritons into polaritons of the signal and idler modes, whereas, in the second case, at the initial stage, the density of pump polaritons of the first pulse initially increases due to the conversion of pairs of signal and idler polaritons into pump polaritons. In this case, this increase at the initial stage is steeper than the exponential decrease. Then, as the polariton densities of the signal and idler modes are depleted, in fact, only their exponential decrease remains due to the decay. In general, the evolution of the polariton density ultimately is reduced to a complete disappearance of all the polaritons of the microcavity (Fig. 2c).

It follows from (15) and Fig. 2d that, at \(t \gg {{\gamma }^{{ - 1}}}\), the occurrence of the exponential factor \({{e}^{{ - 2\gamma t}}}\) in the particle densities leads to a situation that the system of polaritons decays with time, and the densities of all the particles vanish. It is also seen that, at \(t \to \infty \), the ultimate values of the polariton densities are no longer possible (solution with the minus sign).

Let us now consider the evolution of the system at initial phase difference θ0 = 0. If the initial density of polaritons of one of the pump pulses, e.g., of the second pulse, is smaller than or equal to the initial density of polaritons of the idler mode (\({{n}_{{p{{0}_{2}}}}} \leqslant {{n}_{{i0}}}\)), then, at a certain relation between the initial parameters of the system, the solution of Eq. (8) has the form \({{n}_{{{{p}_{1}}}}} = {{n}_{{{{p}_{1}}0}}}\exp ( - 2\gamma t)\); i.e., it coincides with the initial condition, which takes place because of the intersection of the two middle roots of the equation \(W({{N}_{{{{p}_{1}}}}}) = {{E}_{0}}\). Therefore, the solution of Eq. (8) will not contain a phase shift. If the two middle roots of the equation \(W({{N}_{{{{p}_{1}}}}}) = {{E}_{0}}\) are not degenerate, two cases of evolution arise. Depending on the relationship between the parameters \({{n}_{{{{p}_{1}}0}}}\), \({{n}_{{{{p}_{2}}0}}}\), \({{n}_{{i0}}}\), and \({{n}_{{s0}}}\), in the first case, the roots are ordered such that \({{y}_{1}} > {{n}_{{{{p}_{1}}0}}} > {{y}_{m}} > {{y}_{4}}\), while, in the second case, \({{y}_{1}} > {{y}_{M}} > {{n}_{{{{p}_{1}}0}}} > {{y}_{4}}\).

If \({{y}_{1}} > {{n}_{{{{p}_{1}}0}}} > {{y}_{m}} > {{y}_{4}}\), the solution of Eq. (8) has the form

$${{n}_{{{{p}_{1}}}}} = {{n}_{{{{p}_{1}}0}}}\exp ( - 2\gamma t)\frac{{1 - \frac{{{{y}_{1}}({{n}_{{{{p}_{1}}0}}} - {{y}_{m}})}}{{{{y}_{1}} - {{y}_{m}}}}{\text{s}}{{{\text{n}}}^{2}}\left( {\mu \sqrt {({{y}_{1}} - {{y}_{m}})({{n}_{{{{p}_{1}}0}}} - {{y}_{4}})} \frac{{1 - \exp ( - 2\gamma t)}}{{2\gamma }}} \right)}}{{1 - \frac{{{{n}_{{{{p}_{1}}0}}} - {{y}_{m}}}}{{{{y}_{1}} - {{y}_{m}}}}{\text{s}}{{{\text{n}}}^{2}}\left( {\mu \sqrt {({{y}_{1}} - {{y}_{m}})({{n}_{{{{p}_{1}}0}}} - {{y}_{4}})} \frac{{1 - \exp ( - 2\gamma t)}}{{2\gamma }}} \right)}},$$
(16)

where

$${{k}^{2}} = \frac{{({{y}_{1}} - {{y}_{4}})({{n}_{{{{p}_{1}}0}}} - {{y}_{m}})}}{{({{y}_{1}} - {{y}_{m}})({{n}_{{{{p}_{1}}0}}} - {{y}_{4}})}}.$$
(17)

In the second case, when \({{y}_{1}} > {{y}_{M}} > 1 > {{y}_{4}}\), we correspondingly obtain

$${{n}_{{{{p}_{1}}}}} = {{n}_{{{{p}_{1}}0}}}\exp ( - 2\gamma t)\frac{{1 - \frac{{{{y}_{4}}({{y}_{M}} - {{n}_{{{{p}_{1}}0}}})}}{{{{y}_{M}} - {{y}_{4}}}}{\text{s}}{{{\text{n}}}^{2}}\left( {\mu \sqrt {({{y}_{1}} - {{n}_{{{{p}_{1}}0}}})({{y}_{M}} - {{y}_{4}})} \frac{{1 - \exp ( - 2\gamma t)}}{{2\gamma }}} \right)}}{{1 - \frac{{{{y}_{M}} - {{n}_{{{{p}_{1}}0}}}}}{{{{y}_{M}} - {{y}_{4}}}}{\text{s}}{{{\text{n}}}^{2}}\left( {\mu \sqrt {({{y}_{1}} - {{n}_{{{{p}_{1}}0}}})({{y}_{M}} - {{y}_{4}})} \frac{{1 - \exp ( - 2\gamma t)}}{{2\gamma }}} \right)}},$$
(18)

where

$${{k}^{2}} = \frac{{({{y}_{1}} - {{y}_{4}})({{y}_{M}} - {{n}_{{{{p}_{1}}0}}})}}{{({{y}_{1}} - {{n}_{{{{p}_{1}}0}}})({{y}_{M}} - {{y}_{4}})}}.$$
(19)

It is seen from Fig. 3 that, in the course of time, the amplitude of oscillations of these solutions decays exponentially and, at \(t \gg {{\gamma }^{{ - 1}}}\), the normalized density of pump polaritons of the first pulse turns to zero.

Thus, it follows from the presented results that the time evolution of the pump polariton density at the initial phase difference of θ0 = π/2 differs from the time evolution at θ0 = 0. Therefore, it is of interest to study peculiarities of the time evolution for an arbitrary value of the initial phase difference θ0. The equation \(W({{N}_{p}}) = {{E}_{0}}\) has four real roots, which we arrange in the order of decreasing \({{y}_{1}} > {{y}_{M}} > {{y}_{m}} > {{y}_{4}}\). The values of these roots are determined by the parameters \({{n}_{{{{p}_{1}}0}}}\), \({{n}_{{{{p}_{2}}0}}}\), \({{n}_{{s0}}}\), \({{n}_{{i0}}}\), and \({{\theta }_{0}}\). In this case, the solution has the form

$${{n}_{{{{p}_{1}}}}} = {{n}_{{{{p}_{1}}0}}}\exp ( - 2\gamma t)\frac{{{{y}_{M}} - \frac{{{{y}_{1}}({{y}_{M}} - {{y}_{m}})}}{{{{y}_{1}} - {{y}_{m}}}}{\text{s}}{{{\text{n}}}^{2}}\left( {\mu \nu \frac{{1 - \exp ( - 2\gamma t)}}{{2\gamma }} \pm f({{\varphi }_{0}},k)} \right)}}{{1 - \frac{{{{y}_{M}} - {{y}_{m}}}}{{{{y}_{1}} - {{y}_{m}}}}{\text{s}}{{{\text{n}}}^{2}}\left( {\mu \nu \frac{{1 - \exp ( - 2\gamma t)}}{{2\gamma }} \pm f({{\varphi }_{0}},k)} \right)}}.$$
(20)

Here, \(f({{\varphi }_{0}},k) = F({{\varphi }_{0}},k) - K(k)\), where \(F({{\varphi }_{0}},k)\) is the incomplete elliptic integral of the first kind with modulus k and parameter φ0, while \(K(k)\) is the complete elliptic integral [48, 49]. Quantities k, φ0, and ν are determined by the relationships

$${{k}^{2}} = \frac{{({{y}_{1}} - {{y}_{4}})({{y}_{M}} - {{y}_{m}})}}{{({{y}_{1}} - {{y}_{m}})({{y}_{M}} - {{y}_{4}})}},$$
$${{\varphi }_{0}} = \arcsin \sqrt {\frac{{({{y}_{M}} - {{y}_{4}})(1 - {{y}_{m}})}}{{({{y}_{M}} - {{y}_{m}})(1 - {{y}_{4}})}}} ,$$
(21)
$$\nu = \sqrt {({{y}_{1}} - {{y}_{m}})({{y}_{M}} - {{y}_{4}})} .$$

It can be seen from (20), (21), and Fig. 4 that the density of pump polaritons of the first pulse, \({{n}_{{{{p}_{1}}}}}(t)\), oscillates and monotonically decreases with time. The spacing between the two nearest points in Fig. 4, which oscillates in the same phase, monotonically grows with time. At the initial phase difference θ0 tending to the value \((2k + 1)\pi {\text{/2}}\) (k = 0, 1, 2, …), the time evolution becomes aperiodic, and there are no oscillations in the polariton density (Figs. 4b, 4c).

Fig. 3.
figure 3

Time evolution of density of pump polaritons of the first pulse \(y = \frac{{{{n}_{{{{p}_{1}}}}}}}{{{{n}_{{{{p}_{1}}0}}}}}\) at the initial phase difference θ0 = 0, as well as at fixed initial densities of pump polaritons of the second pulse, initial polariton densities of the signal and idler modes and decay coefficients: (1) \({{{{n}_{{{{p}_{2}}0}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{p}_{2}}0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 1.5\), \({{{{n}_{{s0}}}} \mathord{\left/ {\vphantom {{{{n}_{{s0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.3\), \({{{{n}_{{i0}}}} \mathord{\left/ {\vphantom {{{{n}_{{i0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.1\), and \(\gamma = 0.01\); (2) \({{{{n}_{{{{p}_{2}}0}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{p}_{2}}0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.2\), \({{{{n}_{{s0}}}} \mathord{\left/ {\vphantom {{{{n}_{{s0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.6\), \({{{{n}_{{i0}}}} \mathord{\left/ {\vphantom {{{{n}_{{i0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.7\), and \(\gamma = 0.01\). Here, \(\tau = {{\mu t} \mathord{\left/ {\vphantom {{\mu t} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}}\).

Full size image
Fig. 4.
figure 4

Time evolution of density of pump polaritons of the first pulse \(y = \frac{{{{n}_{{{{p}_{1}}}}}}}{{{{n}_{{{{p}_{1}}0}}}}}\) in relation to initial phase difference θ0 at fixed initial densities of pump polaritons of the second pulse, polaritons of the signal and idler modes, and decay coefficients: (а) \({{{{n}_{{{{p}_{2}}0}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{p}_{2}}0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.5\), \({{{{n}_{{s0}}}} \mathord{\left/ {\vphantom {{{{n}_{{s0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.3\), \({{{{n}_{{i0}}}} \mathord{\left/ {\vphantom {{{{n}_{{i0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.1\), and \(\gamma = 0.01\); (b) \({{{{n}_{{{{p}_{2}}0}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{p}_{2}}0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.5\), \({{{{n}_{{s0}}}} \mathord{\left/ {\vphantom {{{{n}_{{s0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.3\), \({{{{n}_{{i0}}}} \mathord{\left/ {\vphantom {{{{n}_{{i0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.3\), and \(\gamma = 0.01\); (c) \({{{{n}_{{{{p}_{2}}0}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{p}_{2}}0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.5\), \({{{{n}_{{s0}}}} \mathord{\left/ {\vphantom {{{{n}_{{s0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.3\), \({{{{n}_{{i0}}}} \mathord{\left/ {\vphantom {{{{n}_{{i0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.3\), and \(\gamma = 0.04\). Here, \(\tau = {{\mu t} \mathord{\left/ {\vphantom {{\mu t} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}}\).

Full size image

We note that the polariton densities of the signal and idler modes and of pump polaritons of the second pulse, in the same way, oscillate, decrease with time, and turn to zero at long times \((t \gg {{\gamma }^{{ - 1}}})\).

At arbitrary values of the decay constants \({{\gamma }_{{{{p}_{1}}}}}\), \({{\gamma }_{{{{p}_{2}}}}}\), \({{\gamma }_{s}}\), and \({{\gamma }_{i}}\), solutions of Eqs. (4) can be obtained only numerically. Figure 5 presents plots of the time evolution of the density of pump polaritons the first pulse at arbitrary values of decay constants \({{\gamma }_{{{{p}_{1}}}}}\), \({{\gamma }_{{{{p}_{2}}}}}\), \({{\gamma }_{s}}\), and \({{\gamma }_{i}}\). It can be seen that, in this case, the envelopes of the polariton density monotonically decrease with time, with the decay rate being substantially determined by the relations between the decay constants. Thus, the behavior of the system will not change qualitatively.

Fig. 5.
figure 5

Time evolution of density of pump polaritons of the first pulse \(y = \frac{{{{n}_{{{{p}_{1}}}}}}}{{{{n}_{{{{p}_{1}}0}}}}}\) at the initial phase difference θ0 = 0, as well as at fixed initial densities of pump polaritons of the second pulse, the initial density of polaritons of the signal and idler modes \({{{{n}_{{{{p}_{2}}0}}}} \mathord{\left/ {\vphantom {{{{n}_{{{{p}_{2}}0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 1.5\), \({{{{n}_{{s0}}}} \mathord{\left/ {\vphantom {{{{n}_{{s0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.3\), and \({{{{n}_{{i0}}}} \mathord{\left/ {\vphantom {{{{n}_{{i0}}}} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}} = 0.1\) and different decay coefficients of corresponding polariton states (1) \({{\gamma }_{{{{p}_{1}}}}} = 0.01\), \({{\gamma }_{{{{p}_{2}}}}} = 0.04\), \({{\gamma }_{s}} = \) 0.02, and \({{\gamma }_{i}} = 0.03\); (2) \({{\gamma }_{{{{p}_{1}}}}} = 0.01\), \({{\gamma }_{{{{p}_{2}}}}} = 0.01\), \({{\gamma }_{s}} = 0.02\), and \({{\gamma }_{i}} = 0.02\); and (3) \({{\gamma }_{{{{p}_{1}}}}} = 0.03\), \({{\gamma }_{{{{p}_{2}}}}} = 0.04\), \({{\gamma }_{s}} = 0.05\), and \({{\gamma }_{i}} = 0.03\). Here, \(\tau = {{\mu t} \mathord{\left/ {\vphantom {{\mu t} {{{n}_{{{{p}_{1}}0}}}}}} \right. \kern-0em} {{{n}_{{{{p}_{1}}0}}}}}\).

Full size image

CONCLUSIONS

Therefore, upon pumping of the lower polariton branch at two close points of the dispersion law and taking into account the decay in relation to the initial phase difference, the initial density of pump polaritons of both pulses, and the initial densities of the signal and idler polaritons, various evolution regimes of the polariton system are possible: oscillatory and exponential decay of the amplitude of oscillations of the corresponding polariton states. Taking into account the decay leads to the disappearance of polaritons in the system.