The results presented in this and subsequent chapters show the role of special laws of chain reaction kinetics in flame propagation, explosion, and detonation. In all combustion regimes, a chain avalanche determines the specific character of the temperature dependence of the reaction rate, which is of decisive importance in all patterns of combustion processes from combustion to detonation. The patterns and laws of nonisothermal chain reactions are determined by the simultaneous realization of a chain avalanche and avalanche heat release. The main difference between the kinetics of chain combustion processes and the kinetics of other types of processes is primarily that the chain mechanism determines extremely high rates and self-accelerations that are impossible in reactions of other types. Chain combustion reactions are characterized not only by high rates, but also by their extremely strong temperature dependence, which determines the abrupt transition of combustion into explosion and detonation.

In this chapter, we will discuss the patterns and kinetic laws of combustion reactions and specificities of the temperature dependence of the rate of the process.

1 THE DETERMINING ROLE OF CONCENTRATION CHANGES IN THE TEMPERATURE DEPENDENCE OF THE REACTION RATE

The Arrhenius law, used in combustion theory and chemical kinetics to describe the temperature dependence of reaction rates, refers to the temperature dependence of rate constants only. This law actually expresses the change with temperature in the fraction of particles capable of overcoming the energy barrier of an elementary reaction. The rates of these reactions, equal to the product of the rate constants and reagent concentration, depend on changes not only in the aforementioned fraction of particles, but also in the reagent concentrations, differently from the Arrhenius law. In this and the next two sections, we will discuss the specificities of the temperature dependence of the rates of elementary reactions, including the contribution of changes in the reagent concentrations during combustion.

As noted in Chapter I, since, in the traditional theory of thermal combustion and in works carried out within the framework of this theory, the temperature dependence of the rate of gas-phase reactions was represented by the Arrhenius function (e.g., [1–17]), the parameters formally assigned to this function do not correspond to their physical meaning and change depending on the process conditions even in simple non-chain reactions. Taking into account changes in the reagent concentrations during the reaction, caused by a change only in gas density (e.g., [4]), with temperature does not reflect the real features of the kinetics. Let us first consider the rate of a one-component reaction of the first kinetic order:

$$-\frac{{{\text{d}}C}}{{{\text{d}}t}} = W = k\left( {T,t} \right)C\left( {T,t} \right),$$
(1.IX)

where k, C, T, and t are the rate constant, concentration, temperature, and time, respectively, and n is the kinetic order of the reaction. This equation implies

$$\frac{{\partial W}}{{\partial T}} = C\left( {T,t} \right)\frac{{\partial k\left( {T,t} \right)}}{{\partial T}} + k\left( {T,t} \right)\frac{{\partial C\left( {T,t} \right)}}{{\partial T}}.$$
(2.IX)

It can be seen that the traditional identification of the temperature dependence of the reaction rate with the dependence of the rate constant only means illegally ignoring the second term in Eq. (2.IX). The concentration of the initial reagent does not change during the reaction only at zero kinetic order, which is not realized in gas-phase reactions. The reaction model adopted in the theory of thermal ignition, e.g., [1–3, 5], which takes into account the heat release, but without the reagent consumption, also contradicts the laws of conservation of energy and mass.

Equation (1.IX) implies that, at a constant temperature, changes in the reagent concentration and the reaction rate are expressed as follows:

$$C\left( {T,t} \right) = {{C}_{0}}{{{\text{e}}}^{{-k\left( {T,t} \right)t}}},$$
(3.IX)
$$W = k\left( {T,t} \right){{C}_{0}}{{{\text{e}}}^{{-k\left( {T,t} \right)t}}},$$
(4.IX)

where \({{C}_{0}}\) is the initial concentration.

We see that, in expression (4.IX), the rate constant with its temperature dependence enters not only into the factor at С0, but also into the exponent. Hence, it is already obvious that the traditional consideration of the temperature dependence of rate taking into account only \(k\left( {T,t} \right)\), i.e., ignoring the factor С0\({{{\text{e}}}^{{-k\left( {T,t} \right)t}}}\), is unacceptable. Equations (3.IX) and (4.IX) imply that the reaction occurring at two constant temperatures and the same initial reagent concentration are described by the following equations:

$${{C}_{1}}\left( t \right) = {{C}_{0}}{{{\text{e}}}^{{-{{k}_{1}}t}}},$$
(3a.IX)
$${{C}_{2}}\left( t \right) = {{C}_{0}}{{{\text{e}}}^{{-{{k}_{2}}t}}}t,$$
(3b.IX)
$${{W}_{1}} = {{k}_{1}}{{C}_{0}}{{{\text{e}}}^{{-{{k}_{1}}t}}},$$
(4a.IX)
$${{W}_{2}} = {{k}_{2}}{{C}_{0}}{{{\text{e}}}^{{-{{k}_{2}}t}}},$$
(4b.IX)

Subscripts 1 and 2 refer to the two accepted temperatures. The ratio of rates at these temperatures at the same time after the onset of the reaction is

$$\frac{{{{W}_{2}}}}{{{{W}_{1}}}} = \frac{{{{k}_{2}}}}{{{{k}_{1}}}}{{{\text{e}}}^{{({{k}_{1}}-{{k}_{2}})t}}}.$$
(5.IX)

The rate would depend on temperature according to the Arrhenius law, if, with a change in temperature, the ratio \(\frac{{{{W}_{2}}}}{{{{W}_{1}}}}\) were equal to \(\frac{{{{k}_{2}}}}{{{{k}_{1}}}}\). However, we see that \(\frac{{{{W}_{2}}}}{{{{W}_{1}}}}\) is not equal to \(\frac{{{{k}_{2}}}}{{{{k}_{1}}}}\) even after the same time since the start of the reaction, because, due to the difference in temperatures, \({{k}_{1}}\) is not equal to \({{k}_{2}}\) and the rates turned out to be different in accordance with expression (5.IX).

Instead of Eqs. (3.IX) and (4.IX), the changes in concentration and rate with temperature are expressed as follows:

$$C\left( {T,t} \right) = {{C}_{0}}{\text{exp}}~\left[ {-\mathop \smallint \limits_{{{t}_{0}}}^t k\left( T \right)} \right]{\text{d}}t,$$
(6.IX)
$$W\left( {T,t} \right) = k\left( T \right)~{{C}_{0}}{\text{exp}}\left[ {-\mathop \smallint \limits_{{{t}_{0}}}^t k\left( T \right)} \right]{\text{d}}t.$$
(7.IX)

It is obvious that the function \(C\left( {T,t} \right)\) largely determines the temperature dependence of the rate of reactions of other kinetic orders except zeroth. For example, second-order reactions in a stoichiometric mixture are expressed as

$$C\left( {T,t} \right) = \frac{{{{C}_{0}}}}{{1 + {{C}_{0}}\int\limits_0^t {k\left( {T,t} \right){\text{d}}t} }},$$
(8.IX)
$$~~W\left( {T,t} \right) = k\left( T \right)~\frac{{C_{0}^{2}}}{{{{{\left[ {1 + {{C}_{0}}\int\limits_0^t {k\left( T \right){\text{d}}t} } \right]}}^{2}}}}.$$
(9.IX)

Thus, even in elementary reactions, the contribution of the function \(C\left( {T,t} \right)\) to the temperature dependence of the rate is very large and varies depending on the mechanism (in this case, the kinetic order) of the reaction. In chain reactions, the role of changes in С(Т) is incomparably higher.

Ignoring the temperature dependence of concentration in the expression for the rate turned out to be the main reason why the observed high rates of combustion and explosion reactions of gases and their strong temperature dependence could not be explained until recently.

2 SPECIFICITIES OF THE TEMPERATURE DEPENDENCE OF RATE CONSTANTS OF BIMOLECULAR REACTIONS

The leading role in the processes of gas combustion and explosion is played by reactions of the second and first kinetic orders. The temperature dependence of the rate constants of such reactions, expressed by the Arrhenius function,

$$k\left( T \right) = {{k}^{0}}{{{\text{e}}}^{{-~\frac{E}{{RT}}}}},$$
(10.IX)

reflects an obvious pattern: the higher the activation energy, the smaller the rate constant at a given temperature. Intermolecular reactions themselves cannot provide combustion regimes not only because of the very small rate constants, but also because, even with a strong increase in temperature, e.g., by the heat of a shock wave, their rate constants almost do not increase (Fig. 1. IX). Therefore, contrary to the generally accepted views, until recently (e.g., [1–5]), intermolecular reactions in flame propagation, explosion, and detonation are not actually accelerated and are not themselves capable of supporting these processes even after strong initiation. The attribution of unrealistic values of activation energy and preexponential factors to hypothetical one-stage reactions in the thermal theory of combustion allows only a conditional description of the observed rates in narrow temperature ranges, but does not even approximately explain the inhibition inherent in combustion, the sharp transition from low rates to an explosive regime, super-equilibrium concentrations of atoms and radicals, and abrupt transition from combustion to explosion.

Fig. 1.
figure 1

IX. Temperature dependence of the function k/k0 = e–E/RT at activation energies of (1) 25.2, (2) 150, and (3) 225 kJ/mol.

Full size image

In [18, 19], attention was drawn to the fact that a quantitative measure of the temperature dependence of the rate is its change with a unit change in temperature, i.e., sensitivity of the rate to temperature changes. Accordingly, along with the dependence of the rate constant on the activation energy, its important characteristic is also an increase or decrease in the absolute value of this kinetic parameter with a unit increase or decrease in temperature, i.e., the quantity \({{\beta }}\) \( = \frac{{\partial k}}{{\partial T}}\). The function \({{\beta }}\) also determines the change in the competition between different stages of the process at changing temperatures. According to (10.IX), the temperature dependence of the rate constant is

$$\beta = \frac{{\partial k}}{{\partial T}} = {{k}^{0}}{{{\text{e}}}^{{-\frac{E}{{RT}}}}}\frac{E}{{R{{T}^{2}}}} = k\frac{E}{{R{{T}^{2}}}}.$$
(11.IX)

At high activation energies inherent in intermolecular reactions, the exponential factor in expression (10.IX) is extremely small. In addition, since k0 cannot exceed the double-collision frequency, the rate constants for reactions between valence-saturated molecules are also extremely low. Therefore, the \({{\beta }}\) of intermolecular reactions is extremely small; i.e., the rate constants for such reactions depend on temperature extremely weakly. In developed combustion, intermolecular reactions actually do not play a role.

To clarify the dependence of \({{\beta }}\) on the activation energy, which is different in different reactions, consider the quantity \(\frac{{\partial {{\beta }}}}{{\partial E}}\), obtained from expression (11.IX):

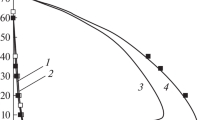
$$\frac{{\partial {{\beta }}}}{{\partial E}} = {{k}^{0}}{{{\text{e}}}^{{-\frac{E}{{RT}}}}}\frac{1}{{R{{T}^{2}}}}\left( {1-\frac{E}{{RT}}} \right)$$
(12.IX)

and showing the nature of the change in the temperature dependence of the rate constant in reactions with different activation energies. If \(E > RT\), then the value of \(\frac{{\partial {{\beta }}}}{{\partial E}}\) is negative and, therefore, the greater the activation energy, the smaller \({{\beta }}\), i.e., the weaker the temperature dependence k(T), as shown in Fig. 1.IX.

In the combustion processes of the vast majority of gases, the activation energies of even the reactions of atoms and radicals usually exceed 25 kJ/mol [20]. The combustion temperature of gases rarely exceeds 3000 K. Since, therefore, in these processes, Е > RT, we can conclude that the greater the activation energy, the weaker the temperature dependence of the rate constant, contrary to generally accepted ideas. From the aforesaid and from Fig. 2.IX it follows that intermolecular reactions, the activation energy of which exceeds 160 kJ/mol, are characterized not only by very small rate constants, but also by their extremely small increase with increasing temperature. Therefore, the rates of such reactions also increase only slightly.

Fig. 2.
figure 2

IX. Temperature of the inflection of the function k(Т) and the quantity \({{{{\beta }}}_{{{\text{max}}}}}\) vs. activation energy of (1) 67 and (2) 210 kJ/mol; (3) the value of k/k0 at the inflection point.

Full size image

Let us now consider the dependence of \({{\beta }}\) on T and k0. At a given activation energy, the temperature dependence k(T) is the strongest at the temperature corresponding to the inflection in the graph of the function k(T), as can be seen from Fig. 2.IX. The inflection temperature corresponds to the zero of the temperature derivative of the function (11.IX) and is equal to [18, 19, 21]

$${{T}_{{{\text{infl}}}}} = \frac{E}{{2R}}.$$
(13.IX)

This means that, even for the reaction of an active radical, e.g., H atoms with propane, with an activation energy of only 31.3 kJ/mol, the progressive growth of the rate constant with temperature remains up to 1880 K. Expressions (10.IX) and (13.IX) also imply that, regardless of the activation energy, the rate constant at the inflection temperature is equal to [18, 19]

$$k{{\left( T \right)}_{{{\text{infl}}}}} = \frac{{{{k}^{0}}}}{{{{{\text{e}}}^{2}}}} = \frac{{{{k}^{0}}}}{{7.4}}.$$
(14.IX)

From Eq. (11.IX) it is obvious that, for a given activation energy, the larger \({{k}^{0}}\), the greater \({{\beta }}\). Therefore, the large effective preexponential factor, determined from the data on the gross reaction, causes a strong temperature dependence of the effective rate constant. But this value of empirical k0 does not correspond to the physical meaning of the preexponential factor of the rate constant.

3 TEMPERATURE DEPENDENCE OF THE EFFECTIVE VALUE OF RATE CONSTANTS

As noted in Chapter I, many provisions and methods of the theories of combustion and chemical kinetics were based on the incorrect idea of a strong temperature dependence of the rate at high activation energies (e.g., [1–3, 5]). Its fallacy is illustrated by Fig. 1.IX, from which it is clear that, on the contrary, the higher the activation energy, the weaker the temperature dependence of the rate constant.

These ideas about the character of the temperature dependence of the rate and the rate constant are largely related to the method of experimental determination of these quantities. The process was causelessly presented (and is often presented today) as a one-step reaction. Empirical values of activation energies (Еemp) and preexponential factor (\(k_{{{\text{emp}}}}^{0}\)) are determined from the dependence of the logarithm of the measured reaction rate (or a proportional quantity) on the reciprocal temperature, unreasonably assuming that the temperature dependence of the reaction rate corresponds to the Arrhenius law. The logarithmic function often simulates a linear dependence. However, since the reaction rate is equal to the product of the rate constants and concentrations, under strict consideration in these coordinates, linear anamorphosis cannot be obtained. In addition, since the combustion reaction rates are large and strongly depend on temperature, the empirical values of \(k_{{{\text{emp}}}}^{0}\) and Еemp found in this way turn out to be very large and contradict the physical meaning: the values of \(k_{{{\text{emp}}}}^{0}\) are thousands of times greater than the number of binary collisions, the activation energy and, accordingly, the exponent is overestimated several-fold. Therefore, the rate constants turn out to be overestimated by orders of magnitude. As a result of this approach, the values of Еemp and \(k_{{{\text{emp}}}}^{0}\) assigned to the same reaction in different works vary widely.

It was also found that the misconceptions that still exist about the stronger temperature dependence of the rate constant at high activation energies are the result of considering not the absolute growth of the constant, but its relative growth, \(\frac{{\Delta k}}{k}\) (e.g., [3, 5]). However, all experiments, in accordance with the fundamental law of mass action, show that the reaction rate is proportional not to the relative value of the rate constant, but to its absolute value, which must enter into the kinetic equations.

The misconceptions about the strong temperature dependence of the reaction rates at high activation energies have served as a basis for the conceptions of a “narrow reaction zone” and the “method of expansion of the exponential of the rate constant,” which use the Arrhenius law to describe the temperature dependence of the rate [3], as well as, e.g., the works [2, 5, 22]. As shown above, the methods of narrow reaction zone and expansion of the exponential of the Arrhenius law are unjustified. In addition, as can be seen from Figs. 1.IX and 2.IX, in the model of intermolecular reaction adopted in [2, 3, 5], the rate constant changes extremely little with temperature, and the narrow zone is not formed. From these figures and from expression (11.IX) it is obvious that, at high activation energies and, therefore, small rate constants, the temperature dependence of their absolute value will also be very weak. Therefore, the thermal self-acceleration of such reactions is insignificant. The sharp increase in the rate with increasing temperature in the experiment is caused by a fundamentally different law, discussed in this chapter.

Comparison of the observed sharp increase in the reaction rate upon heating with the \({{\delta }}\)-function [2, 3] is extremely formal, since there is nothing in common between the \({{\delta }}\)-function and combustion. Note that the \({{\delta }}\)-function model, i.e., the point charge density at one point is not rigorous: even the smallest charged particle, an electron, is not point-wise.

4 REASONS FOR THE DEVIATION OF CALCULATED TEMPERATURE DEPENDENCES OF RATES FROM REAL ONES

The general reason for deviations between calculated combustion reaction rates and real ones is the neglect of changes in concentrations with temperature and incorrect consideration of these changes. For example, in [23, 24] it is said that the temperature dependence of the rate of a number of branching chain processes “obviously should follow the Arrhenius law.” However, the reaction rate is equal to the product of the rate constant and concentrations, and the temperature dependence of this product cannot in any way be the same as the dependences of the factors separately. It is also stated that the temperature dependences of the rates of the limiting stage and self-heating of the chain process are generally the same (e.g., [23]). In reality, these rates refer to different physical quantities and, even for this reason only, cannot be the same. In addition, self-heating proceeds simultaneously with, e.g., heat release from recombination. Particularly incorrect are the neglect of the temperature dependence of the rate of change in the CC concentration and statements on this basis about a stronger dependence of the rate on temperature than on the concentrations of active particles [3, 5, 24]. This was the reason for denying the chain nature of gas combustion with strong self-heating. Another consequence of this denying is that the values of the activation energy of the same reaction, determined from the semi-logarithmic anamorphosis of the dependence of the rate on the reciprocal temperature, turn out to be dependent on the combustion conditions [25–29]. The values of the activation energy determined from the temperature dependence of the overall process assuming its first order usually turn out to be excessively large and sometimes exceed 700 kJ/mol. The preexponential factors are also unnaturally large. This is the result of a wrong assumption that the combustion reaction is a one-step process. Of course, the Arrhenius function also does not describe the abrupt acceleration of the reaction during the transition to an explosion.

In the monographs [1, 30], the following expression for the rate of the chain process is given:

$$W = ~\frac{{A{\text{exp}}\left( {-~\frac{E}{{RT}}} \right)}}{{1-B{\text{exp}}\left( {-~\frac{{{{E}_{1}}}}{{RT}}} \right)}},$$
(15.IX)

where E and Е1 are the effective activation energies, A and B are some temperature-independent quantities, and R is the gas constant. The physical meaning of the quantities A and B is not explained. The temperature dependence of the reagent concentration is not taken into account. In this formula, the reaction rate does not explicitly depend on time. The expression was obtained based on the formula for the stationary length of reaction chains [30–32]:

$$\nu = \frac{\alpha }{{\delta - \beta }},$$

where α, β, and δ are the probabilities of chain continuation, termination, and branching, respectively. However, this formula, also used by other authors [22, 33], does not correspond to the real process, since, if \(\delta < \beta \), the chain length turns out to be negative, which is meaningless.

5 LAW OF TEMPERATURE DEPENDENCE OF COMBUSTION REACTION RATE

An important manifestation of the temperature dependence of the rate of gas combustion reactions [34, 35] it that it is incomparably stronger than the exponential dependence in the Arrhenius law and has a qualitatively different functional nature. This feature is determined by the previously ignored role of the chain avalanche of chain carriers in the temperature dependence of the rate of combustion reactions and is manifested, e.g., in the fact that the reaction rate in a stoichiometric mixture of H2 and O2 at 1 atm and 823 K in a quartz reactor washed with a KCl solution is practically unmeasurable (Fig. 7 in the monograph [36]). Upon heating to 838 K, the rate of the elementary reaction (0) increases by only 5%. However, the experimental results indicate that, with such heating, the mixture spontaneously ignites and burns out in small fractions of a millisecond. Thus, the real combustion rate depends on temperature much more strongly than it follows from the Arrhenius function previously used in the theory. Other differences and examples are discussed in this chapter and in the chapters dealing with explosion and detonation.

The study of the role of atoms and radicals in combustion, as well as the analysis of chain combustion equations, showed [34, 35, 37–40] that the temperature dependence of the combustion rate is primarily due to the extremely strong temperature dependence of the rate of change in the CC concentrations. The character of this dependence follows from the discussion below.

The O2 consumption rates, i.e., the rates of the chain process, are described by the equation

$$\begin{gathered} W = -{\text{d}}\left[ {\text{B}} \right]{\text{/d}}t = {{{{\omega }}}_{0}} + \left\{ {{{k}_{1}} + {{k}_{6}}\left[ {\text{M}} \right]} \right\}~\left[ {\text{B}} \right]n \\ = {{{{\omega }}}_{0}} + {{k}_{{\text{c}}}}\left[ {\text{B}} \right]n, \\ \end{gathered} $$
(16.IX)

where \({{k}_{{\text{c}}}}\) is the quantity in the curly bracket, the numbers of the constants correspond to the numbers of reactions in Section 2 of Chapter II, and n is the CC concentration, whose rate of change, as we saw in Chapters II–IV, is

$${\text{d}}n{\text{/d}}t = {{\omega }_{0}} + (f-g)n = {{\omega }_{0}} + \varphi n.$$
(17.IX)

The meaning of the quantities \({{{{\omega }}}_{0}}\), f, and \(g\) was explained in previous chapters. From Eq. (17.IX) it is clear that, at each moment of time and for each given values of f and \(g\), the rate of change in the concentration n is in feedback with this concentration n itself. Moreover, if f > \(g\), then the feedback is positive and, therefore, n depends exponentially on the difference f – \(g\), which is in the positive exponent, and increases over time with progressive acceleration even at a constant temperature. The quantity f includes the effective value of the chain branching rate constant kb with its Boltzmann factor:

$$f = 2{{k}_{1}}\left[ {\text{B}} \right] = 2k_{1}^{0}{{{\text{e}}}^{{-~\frac{{{{E}_{1}}}}{{RT}}}}}\left[ {\text{B}} \right],$$
(18.IX)

Since, according to Eqs. (16.IX) and (17.IX), n and W depend exponentially on f, which, in turn, depends exponentially on temperature, the temperature dependences of n and W for f > \(g\) are expressed by exponentials whose positive exponent is the Arrhenius function with the activation energy of the limiting stage. This dependence in the form of the “Boltzmann factor in a positive exponent” occurs at each given temperature. Therefore, it is also takes place upon combustion.

After the initial stages of ignition, i.e., at t > t0 ≅ 2.5/\({{\varphi }}\), the value of \({{\omega }}\)0 in Eqs. (16.IX) and (17.IX) can be neglected, integration of Eq. (17.IX) taking into account the expression of f according to formula (18.IX) and the temperature dependence of kb leads to the expression [34, 35]

$$n = {{n}_{0}}{\text{exp}}\mathop \smallint \limits_{{{t}_{0}}}^t \left[ {{{f}_{0}}\exp \left( {-\frac{{{{E}_{{\text{b}}}}}}{{RT}}} \right) - g} \right]{\text{d}}t.$$
(19.IX)

Here, n0 is the CC concentration at t0, Eb is the branching activation energy, and f0 is equal to 2\(k_{{\text{b}}}^{0}\)[В], where \(k_{{\text{b}}}^{0}\) is the preexponential factor of the rate constant kb.

Substituting expression (19.IX) into Eq. (16.IX) for the process rate, we obtain [34, 37]

$$\frac{W}{{\left[ {\text{B}} \right]}} = {{k}_{{\text{b}}}}{{n}_{0}}{\text{exp}}\mathop \smallint \limits_{t0}^t \left[ {{{f}_{0}}{\kern 1pt} \exp \left( {-\frac{E}{{RT}}} \right)-g} \right]{\text{d}}t.$$
(20.IX)

Thus, with increasing temperature, the reaction rate increases exponentially with a positive exponent containing the Boltzmann factor. In this case, the exponent also increases exponentially over time. This specific character of the extremely strong temperature dependence of the reaction rate, confirmed by the experiment [19, 39, 40], determines the observed extremely strong increase in the rate of chain combustion reactions with temperature and has no analogues.

In general, the quantitative inverse relationship between ni and \(\frac{{\partial {{n}_{i}}}}{{\partial t}}\) is taken into account by a system of equations relating to different types of reactions of active particles, including reactions between themselves [41]. The products of the concentrations of active particles and molecular reagents, as well as reaction rate constants, enter into the values of the rates Wj of elementary reactions on the right-hand side of the equations, relating to all components. The presence of a diffusion term does not eliminate this feedback. The system of equations that takes into account the reactions of all components, as well as relating to one active particle, is, generally speaking, nonlinear. However, at each point in space and at each moment of time, the behavior of its solutions is determined by the properties of the linearized system. Diffusion terms also contribute to these properties. The concentrations of all active particles vary according to the law ехр(\({{\Phi }}\)t), where Φ plays the role of criterion φ in formula (18.IX) and is equal to the difference between quantities f1 and \(g\)1, which are analogues of f and \(g\). The products of rate constants and concentrations related to chain branching and chain termination enter into Φ with a positive and negative sign, respectively. A positive value of Φ indicates that the branching rate exceeds the termination rate. A negative Φ means an excess of termination rate over the branching rate. It is obvious that the rate constants entering into Φ and, therefore, the value of Φ vary with temperature. However, the exponential dependence of the concentrations of active particles on \({{\Phi }}\)t remains. The branching rate and, therefore, the values of f1 with their Boltzmann factors depend on temperature much more strongly than the termination rates and, therefore, \(g\)1. Hence, if f1 > \({{g}_{1}}\), then, with increasing temperature, the reaction rate actually increases at a “double exponential” rate, similar to that shown by Eq. (20.IX).

Since most gas combustion reactions proceed along a branching chain path, this law applies to most combustion reactions.

Expression (20.IX) takes into account that, in the chain combustion regime, the increase in the rate of the chain process with increasing temperature is caused not only by an increase in the rate constant kb preceding n0, but to an even greater extent by a strong increase in the concentration of chain carriers, in accordance with the exponential factor, which contains in the positive exponent the quantity f and, therefore, the constant \({{k}_{{\text{b}}}}\) with its Boltzmann factor. With increasing temperature, the integrand in (20.IX) increases exponentially, because the first term in the square brackets is larger than the second and increases faster with increasing temperature. The exponential factor after \({{n}_{0}}\) increases even faster. This character of self-acceleration of the reaction is demonstrated in Fig. 3.IX. The curves 1–5 in the figure represent the progressive increase in the rate at the initial stages of a branching chain reaction at constant temperatures T1 > T2 > T3 > T4 > T5. With the transition from temperature to temperature, the branching factor \({{\varphi }}\) decreases. The curve P in Fig. 3.IX corresponds to the change in the rate with temperature. The adiabatic compression that occurs at very high rates further heats the mixture and accelerates the reaction.

Fig. 3.
figure 3

IX. Time dependence of the rate of the process at constant values of the branching factor \({{\varphi }} \times {{10}^{{-4}}}\) equal to (1) 0.514, (2) 0.367, (3) 0.220, (4) 0.147, (5) –0.147, (6) ‒0.220, (7) –0.367, and (8) –0.514 s–1, as well as (red curve P) during self-heating.

Full size image

Thus, by taking into account the multiplication of active particles, we explained not only the high rates and self-acceleration of reactions, but also their extremely strong dependence on temperature. Since most gas combustion reactions proceed according to the branching chain mechanism, this law applies to most gas-phase combustion processes. Quantitative verification of expression (20.IX) by experiment, as well as the difference in the effect of self-heating and multiplication of active particles on the acceleration of the chain reaction will be discussed in Section 10.

6 DIFFERENCE IN ENERGY EXCHANGE OF SELF-ACCELERATION UPON CHAIN BRANCHING AND INCREASE IN TEMPERATURE

The difference between self-acceleration from an increase in temperature and from chain branching can be considered using the function of the equilibrium distribution of particles by energy. In Fig. 4.IX this distribution function is shown (Boltzmann distribution) at two temperatures. On the abscissa axis, ЕМ corresponds to the activation energy of the reaction of the initial molecules with each other, while ЕR corresponds to the activation energy of the reaction of the initial molecules with the chain carriers. During chain ignition, even at a constant temperature, i.e., without shifting the energy distribution curve, there is a progressive increase in the concentrations of active particles—chain carriers. Accordingly, if the CC multiplication rate exceeds their loss rate, then the proportion of molecules that react with these active particles also progressively increases; i.e., there is an increasing self-acceleration of the chain process, which does not require self-heating. This means that, even if the temperature is constant and the proportion of molecular reagents corresponding to the area between curve 1, the abscissa axis, and the vertical dashed line ЕR is constant, the rate of the chain process increases due to the CC multiplication. It can be seen from the figure that the fraction of molecular reagents capable of reacting with each other at a temperature Т1 corresponds to a very small area enclosed between curve 1, the abscissa axis, and the vertical dashed line ЕМ. At real activation energies of intermolecular reactions, this fraction is much smaller than shown in the figure.

Fig. 4.
figure 4

IX. Equilibrium particle energy distribution at two temperatures; ЕR and ЕM are the activation energies of the reactions of the initial molecules with radicals and with each other.

Full size image

The differences in the characteristics of self-acceleration of reactions with chain and non-chain mechanisms are extremely significant under nonisothermal conditions. Upon the self-heating to temperature Т2, the distribution function shifts to the right. The number of initial molecules capable of reacting with each other corresponds to a slightly larger area limited by curve 2, the abscissa axis, and the same vertical dashed line ЕМ. The increase in the proportion of initial molecules capable of reacting with each other causes the self-acceleration of the intermolecular reaction, i.e., thermal self-acceleration. The area bounded by curve 2, the x axis, and the same vertical dashed line is much smaller than the area enclosed between curves 1 and 2 to the right of their intersection point. This means that the increase in the number of particles capable of entering into an intermolecular reaction caused by self-heating is incomparably smaller than the number of all heated molecules; i.e., the energy released in the form of heat is mainly dissipated unproductively for the reaction self-acceleration. Indeed, this heat warms up all components, including reaction products. However, the energy of the overwhelming majority of heated initial molecules is still not enough to overcome the energy barrier and enter into a reaction. The released heat is transferred to the environment and dissipates. Therefore, the rate of molecular reaction during self-heating increases extremely little.

In contrast to the proportion of molecules entering into intermolecular reactions, the proportion of molecules capable of reacting with atoms and radicals in Fig. 4.IX corresponds to the area limited by the same particle energy distribution curves, the abscissa axis, and the vertical dashed line ER, not ЕМ. It can be seen that the probability of a reaction of a molecule of the initial reagent in a collision with an active particle, due to the low activation energy, is much greater than the probability of a reaction in a collision with a valence-saturated molecule.

It is also seen from Fig. 4.IX that, as the temperature increases from Т1 to Т2, the increase in the proportion of molecules capable of reacting with active particles is much greater than the increase in the proportion of molecules capable of reacting with each other. At atmospheric and elevated pressures, heat is released mainly in cycles of chain propagation at all pressures.

The difference in the physicochemical mechanisms of using internal energy for combustion also determines the difference between all other combustion characteristics.

In a branching chain process, with increasing temperature, not only the proportion of particles capable of reacting increases, but the number of active particles as well, which, in turn, greatly accelerates the combustion reaction. This phenomenon is considered in the next section.

7 CHANGE IN THE TEMPERATURE DEPENDENCE OF THE REACTION IN A SPREADING FLAME

Flame propagation proceeds by the layer-by-layer self-ignition of the mixture, initiated by a suitable flame. In contrast to the gas ignition, discussed in Chapter III, which is caused by heating only by an external source, the layer-by-layer self-ignition ignition during flame propagation is initiated not only by the heat from an external source, but also by the flow of free atoms and radicals from a suitable combustion zone.

In Chapter II, experimental data were presented along with the reaction equation outside the ignition region:

$${{W}_{{{\text{st}}}}} = -\frac{{{\text{d}}\left[ {{{{\text{O}}}_{2}}} \right]}}{{{\text{d}}t}} = {{{{\omega }}}_{0}}\left\{ {1 + \frac{{{{k}_{1}}\left[ {{{{\text{O}}}_{2}}} \right]}}{{g-f}}\left[ {1-{{{\text{e}}}^{{-\left( {g-f} \right)t}}}} \right]} \right\},$$
(9.II)

showing the tendency of a slowly increasing reaction rate to reach a limit at each temperature. In this equation, f and \(g\) are the rates of chain branching and termination at unit concentrations of chain carriers. With increasing temperature, due to its stronger temperature dependence, f approaches \(g\), as a result of which the rate, which is stationary at each temperature, increases hyperbolically. With a further increase in temperature, the square bracket in (9.II) and the denominator preceding this bracket tend to zero, and their ratio, according to L’Hopital’s rule, tends to unity. After this, the time dependence of the rate is described by Eq. (7.II), reflecting the exponential increase in the rate of an isothermal reaction; chain self-ignition occurs, which is accompanied by increasing self-heating.

The difference between the mechanism of flame propagation and the ignition mechanism described above, caused only by the heat of an external source, is that the fresh mixture in the spreading flame is fed by a stream of active particles, primarily H atoms, which enter into a reaction of the replacement of the HO2 radical, formed in the trimolecular termination reaction (VI), with the active radical OH:

$${\text{H + H}}{{{\text{O}}}_{{\text{2}}}}{\text{ = 2OH}}{\text{.}}$$
(IХ)

This reduces the specific termination rate, denoted in Eq. (20.IX) by \(g\), since, as a result of reaction (IX), the rate of trimolecular termination decreases. Thus, the difference \(g\) – f decreases more slowly.

After the time t exceeds 4/(\(g\) – f), the second term in the square bracket becomes much smaller than unity and the reaction rate reaches a stationary value. With a further increase in temperature while f approaches \(g\), the ratio of the square bracket to the denominator tends to t according to L’Hopital’s rule.

After f becomes greater than \(g\), the character of the time dependence of CC concentration and W changes qualitatively: the increase in \(n\) becomes exponential according to expression

$$n = {{n}_{0}}\left[ {{{{\text{e}}}^{{\left( {f-g} \right)\left( {t-{{t}_{0}}} \right)}}}-1} \right]\left( {f-g} \right)\left( {t-{{t}_{0}}} \right).~$$
(21.IX)

According to the same law, the rate of the chain process begins to increase progressively. In this reaction regime, it is more convenient to replace the signs of the numerator and denominator in the curly bracket of Eq. (2.III) with the reverse ones. Then, this equation will take the form

$$W = -\frac{{{\text{d}}\left[ {{{{\text{O}}}_{2}}} \right]}}{{{\text{d}}t}} = {{{{\omega }}}_{0}}\left\{ {1 + \frac{{{{k}_{{\text{b}}}}\left[ {{{{\text{O}}}_{2}}} \right]}}{{f-g}}\left[ {{{{\text{e}}}^{{\left( {f-g} \right)t}}}-1} \right]} \right\}.$$
(22. IX)

where \({{k}_{{\text{b}}}}\) is the rate constant for the branching reaction.

Immediately above the critical condition and at the very initial times, when the quantity in the square bracket is still close to zero, the rate of the chain reaction only very slightly exceeds the rate of the sublimit reaction. The characteristic reaction time is still much longer than the heat removal time, and there is practically no self-heating. At these initial times, the progressive self-acceleration of the reaction and ignition in each of the successive layers is caused only by a chain avalanche. But after a fraction of a millisecond, the characteristic time of the reaction and, therefore, heat release, become close to the characteristic time of heat removal, and self-acceleration of the process develops with the joint participation of an increasing chain avalanche and self-heating. This change in the reaction kinetics upon passing through the limit was confirmed by experiment [42, 43] and numerical calculations [44].

The ignition mechanism described above underlies flame propagation. According to this mechanism, ignition also occurs in a detonation wave, in which the external source of heat and active particles is shock compression.

Thus, taking into account the chain nature of the process, the following phenomena are explained: extremely strong temperature dependence of the rate of combustion reactions and ignition by heat from an external source, including that during flame propagation and detonation. The chain mechanism allows one to control the speed of flame propagation and detonation [45].

8 SHARP SELF-ACCELERATION OF THE REACTION UPON PASSING THE LIMIT TEMPERATURE

In a reactor with a diameter of 7.5 cm at 100 kPa, a stoichiometric mixture of H2 and O2 spontaneously ignites above 830 K [40]. Below this temperature, the reaction is incomparably slower and there is no progressive self-acceleration. To clarify the role of changes in the kinetics of CC concentration in the temperature dependence of the reaction rate, let us first consider the reaction at 829 K, at which there is no self-ignition. We choose conditions under which f /\(g\) = 0.99, i.e., the termination is 1% faster than the branching. In Chapter II it was shown that, if \(f < g\), then the quantity n, i.e., in this case, the H atom concentration, reaches a stationary value determined by expression (8.II). When substituting this value of n into formula (9.II) at t > 4/(\(g\) – f), we obtain the following equation for the stationary rate:

$${{W}_{{{\text{st}}}}} = -\frac{{{\text{d}}\left[ {{{{\text{O}}}_{2}}} \right]}}{{{\text{d}}t}}{{{{\omega }}}_{0}}\left\{ {1 + \frac{{{{k}_{b}}\left[ {{{{\text{O}}}_{2}}} \right]}}{{f-g}}} \right\}.$$
(23.IX)

For convenience, we represent the difference \({{\varphi }} = f-g\) as

$$\varphi = 1-g{\text{/}}f.$$
(24.IX)

Using the value of f given by expression (18.IX), we obtain Eq. (23.IX) in a more convenient form:

$${{W}_{{{\text{st}}}}} = {{{{\omega }}}_{0}}\left[ {1 + \frac{1}{{2\left( {g{\text{/}}f-1} \right)}}} \right].$$
(23а.IX)

Since the value of \({{{{\omega }}}_{0}}\) is very small, the rate \({{W}_{{{\text{st}}}}}\) is also extremely small, even if f is smaller than \(g\) by only 1%. Indeed, under these conditions, [O2] = 4.92 × 10–6 mol/cm3. The rate constant k0 is equal to 6 × 1013exp (–26 800K/T) cm3mol–1s–1 [46, 47]. At these values of [H2], [O2], and k0, the value of \({{{{\omega }}}_{0}}\) is close to 10–11 mol cm–3 s–1. Accordingly, the value of \({{W}_{{{\text{st}}}}}\) calculated using expression (23a.IX) is only ~5 × 10–10 mol cm–3 s–1. At this rate, to consume at least 1% O2, it will take about one hundred seconds, which is 250 times longer than the characteristic heat removal time calculated using the well-known Einstein–Smoluchowski formula. Therefore, there is no self-heating.

Let us now consider the kinetics of this process at the same pressure of 100 kPa, but at a temperature Т0 at which branching prevails over termination, but only by 1%; i.e., f/\(g\) = 1.01. Since the rate constant for reaction (I) is 1.9 × 1014exp(–8350 K/T) [19, 20], this requires increasing the temperature by 2° above the previous value. Integrating Eq. (2.II) at the initial stages of the process leads to an expression formally similar to that given in [31]:

$$\left[ {\text{H}} \right] = \frac{{{{{{\omega }}}_{0}}}}{\varphi }({{{\text{e}}}^{{{{\varphi }}t}}} - 1),$$
(25.IX)

but, as was said, with a different dependence of \({{\varphi }}\) on concentrations and temperature. Expression (22.IX) can be written in a form similar to that given in [1]:

$${{W}_{{\text{b}}}} = -~\frac{{{\text{d}}\left[ {{{{\text{O}}}_{2}}} \right]}}{{{\text{d}}t}} = {{{{\omega }}}_{0}}\left[ {1 + \frac{{{{k}_{{\text{p}}}}\left[ {{{{\text{O}}}_{2}}} \right]}}{\varphi }\left( {{{{\text{e}}}^{{{{\varphi }}t}}}-1} \right)} \right].$$
(26.IX)

Under the conditions f > \(g\), the quantity n and the rate Wb at the beginning of the reaction also progressively increase at a constant temperature. This is a chain ignition. As we see, for such ignition to occur, an increase in temperature is not necessary, which is confirmed by the experimental data presented, e.g., in Figs. 3a.VIII and 3b.VIII of Chapter VIII.

Given the values of kb, [O2], and \({{{{\omega }}}_{0}}\) presented above, expression (26.IX) can be written as

$${{W}_{{\text{b}}}} = {{10}^{{ - 11}}}\left[ {1 + 50({{{\text{e}}}^{{\varphi t}}} - 1)} \right].~$$
(26а.IX)

The value of f calculated from Eq. (18.IX) is equal to 7.48 × 104 s–1. According to formula (24.IX), this value of f and the value of f/\(g\) = 1.01 correspond to φ = 748 s–1. Therefore, at 831 K, only 0.004 s after the onset of the chain reaction, its rate actually increases proportionally to e748t. By this time, the value of Wb calculated using expression (26a.IX) is equal to 9.5 × 10–9 mol cm–3 s–1, which is 19 times greater than the stationary rate Wst, i.e., the maximum rate achievable outside the ignition region. After one more millisecond, the rate reaches 2 × 10–8 mol cm–3 s–1 and exceeds the stationary rate Wst more than 40-fold and the value of \({{{{\omega }}}_{0}}\) more than 2000-fold. The described change in reaction kinetics is in agreement with numerical calculations that take into account the key reactions and generally accepted rate constants [41].

We see that an increase in the initial temperature T0 by only 2° above 829 K with passing the value corresponding to a change in the sign of the difference f – \(g\) transfers the kinetics of changes in the CC concentration and the development of the process from stationary to a qualitatively different regime: progressive self-acceleration, providing greater rates. This is a critical phenomenon. Since the new temperature is also assumed to be unchanged, the rapid increase in the reaction rate is caused only by a chain avalanche. At the initial stages, the self-acceleration of the reaction is, indeed, not actually accompanied by self-heating, since, by the time of 0.005 s, only 2 × 10–5 fractions of H2 and O2 have been consumed. Self-heating begins to have effect only with the further development of the chain avalanche, enhancing it further.

Let us now consider the increase in the reaction rate that occurs already in the chain avalanche regime with an increase in temperature, e.g., from 831 to 833 K. In this case, the value of f, according to expression (20.IX), due to the exponential growth of kb, increases by a factor of 1.024. As a result of an increase in temperature by these 2°, φ will increase almost 3.5-fold and become equal to ~2600 s–1. Hence, after, e.g., 0.003 s after the temperature increases from 831 to 833 K, the rate of the process only due to the chain avalanche, according to formula (26.IX), will become equal to 1.25 × 10–6 mol cm3 s–1. This is more than 20 times greater than the rate achieved in the same time after the temperature reached 331 K.

Unlike the chain mechanism, the model of the thermal theory of combustion cannot explain the observed sharp change in the rate of the process when the temperature changes by several degrees. For example, with an activation energy of 220 kJ/mol, an increase in Т0 from 829 K by the same 2° increases the reaction rate by only 3.6%. This is thousands of times less than the increase in the rate with a chain mechanism in the first 0.005 s. In addition, with an activation energy of 220 kJ/mol, the rate of a one-step reaction is several thousand times lower than the observed one. As said above, at the temperatures considered in this example, the characteristic time of the reaction between O2 and H2 is hundreds of times longer than the heat removal time. An increase in its rate by 3–4% cannot lead to satisfying the conditions for thermal ignition.

The heating in the absence of a chain avalanche is so small that it cannot lead to thermal ignition. Indeed, from the above example it is clear that, outside the ignition region, a chain reaction can proceed at any noticeable rate if the rate of chain branching is only slightly lower than the rate of termination, i.e., if f is not much smaller than \(g\). Upon heating, f increases exponentially, while \(g\) decreases slightly. As was shown above, already as a result of slight self-heating, incomparably smaller than that necessary for thermal ignition, f becomes greater than \(g\) and the mixture enters the region of chain ignition and ignites as a result of a chain avalanche.

The high chemical activity of atoms and radicals ensures high reaction rates and heat release and a strong temperature dependence of the rates also in the case of a unbranched chain mechanism [19]. Examples of a chain–thermal explosion in unbranched chain processes are explosions upon the chlorination of hydrogen and the decomposition of hydrazine.

Thus, the theory of nonisothermal chain processes explains the following observed patterns that have not previously found an explanation: high rates of combustion reactions; an extremely strong temperature dependence of the rate of combustion reactions, qualitatively different from the Arrhenius law; the abrupt nature of the change in the rate when varying the initial temperature in the vicinity of the value corresponding to the equality of the rates of chain branching and termination.

9 COMPARISON OF THE THEORY OF TEMPERATURE DEPENDENCE OF COMBUSTION REACTION RATE WITH EXPERIMENT

Dependence (20.IX) was experimentally verified for a model BCP: combustion of H2 with O2 near the first flammability limit [40]. The reaction was conducted in a vacuum installation described in Chapter IV and Chapter X, at two different temperatures, maintained constant with a thermostat in each experiment. High-speed recording of pressure, chemiluminescence, and temperature was carried out (Fig. 5.IX).

Fig. 5.
figure 5

IX. Oscillograms of (1, 1’) pressure, (2, 2') chemiluminescence, and (3, 3') temperature at temperatures of (1, 2, 3) 768 and (1', 2', 3') 773 K.

Full size image

The time of reaching the maximum reaction rate, measured after the induction period, was 0.36–0.5 s, which is thousands of times longer than the heat removal time. We considered small transformation depths at which the O2 consumption can be neglected; i.e., considered the integrand in expression (19.IX) constant at each given temperature. Due to the low pressures of the mixture, only slightly exceeding Р1, heterogeneous chain termination, which removes recombination energy, and a high rate of conductive heat removal, the process occurred in an almost isothermal regime at each given temperature. Since, therefore, self-heating is small and practically the same at given initial temperatures, as can also be seen from the oscillograms, when considering the rate ratio, its contribution could be neglected with high accuracy. This made it possible to write Eq. (20.IX) as

$$\begin{gathered} W{\text{/}}{{[{{{\text{O}}}_{2}}]}_{0}} = \frac{{{{k}_{1}}{{{\left[ {{{{\text{H}}}_{2}}} \right]}}_{0}}}}{{2\left( {1-\frac{{{{P}_{1}}}}{{{{P}_{0}}}}} \right)}} \\ \times \,\,{\text{exp}}\left\{ {\left[ {2k_{1}^{0}{{{\left[ {{{{\text{O}}}_{2}}} \right]}}_{0}}\exp \left( {-\frac{{{{E}_{1}}}}{{RT}}} \right)-{{k}_{{{\text{het}}}}}} \right]\left( {t-{{t}_{0}}} \right)} \right\}. \\ \end{gathered} $$
(27.IX)

In this expression, Е1 is the activation energy of the limiting stage—the event of branching, equal to 70 kJ/mol, and khet is the rate constant of heterogeneous loss of H atoms, equal to 2k1[O2]1, where [O2]1 is the O2 concentration at the first flammability limit, measured in the same experiments, as was shown in Chapter 5. Using formula (27.IX), the ratio between the rates of the chain reaction occurring at the indicated two different temperatures was determined. For example, Table 1.IX shows the results of the experiment and calculations using formula (27.IX). The last column presents the calculated increase in the rate that would occur if its temperature dependence were expressed by the Arrhenius law.

Table 1. IX.  Verification of Eq. (27.IX) by experiment
Full size table

The slight increase of the calculated rate ratio in the second column with time is due to the fact that calculations neglected the O2 consumption and, accordingly, the calculated rate increased with time slightly.

The observed increase in the rate, caused by this increase in temperature, formally corresponds to an activation energy of 460 kJ/mol. However, the activation energy of the limiting stage of the process—reaction (I)—is only 70 kJ/mol. The rate of the process is equal to the rate of the limiting reaction (I), determined by the quantity k1[O2][H]. Therefore, the difference between these two values (390 kJ/mol) is the effective activation energy of the increase in the H atom concentration. We see that, in accordance with the exponential law in the positive exponent in (20.IX), the increase in the H atom concentration is much stronger than the increase in the rate constant for chain branching.

In developing combustion, heat is released mainly in chain propagation cycles due to high reaction rates. Chain termination and, accordingly, heat release also occur in disproportionation reactions in the gas phase, e.g.,

$$\begin{gathered} {\text{O + OH = }}{{{\text{O}}}_{{\text{2}}}}{\text{ + H}}{\text{,}} \\ {\text{OH + H}}{{{\text{O}}}_{{\text{2}}}}{\text{ = }}{{{\text{H}}}_{{\text{2}}}}{\text{O + }}{{{\text{O}}}_{{\text{2}}}}{\text{.}} \\ \end{gathered} $$
(–I)

In these reactions, which proceed with low activation energies [46, 47], the number of free valences decreases. Heat generation does not compensate for the slowing effect of chain termination.

10 VERIFYING THE THEORY OF TEMPERATURE DEPENDENCE OF REACTION RATE BY EXPERIMENT IN A WIDE TEMPERATURE RANGE

Experiments to determine the separate contribution of changes in temperature and CC concentrations to the temperature dependence of the reaction rate were conducted in the range of pressures from several Torr to 1 atm and the range of temperatures from 763 to 2500 K. In [37, 40], the combustion of a stoichiometric mixture of H2 and O2 was performed in a thermostated quartz reactor (Fig. 2.IV of Chapter IV) at constant temperatures of 773 and 768 K and an initial pressure of 2.25 Torr. A microthermocouple was placed in a quartz capillary washed with hydrofluoric acid to reduce heterogeneous recombination and recombination heating. It can be seen from Fig. 5.IX that the difference in heating at given temperatures does not exceed 0.15°, i.e., is less than 3% of the difference in initial temperatures. The recorded maximum temperature increase of 4° is caused mainly by recombination heating of the thermocouple. This is also evidenced by the fact that the maximum heating is achieved only after the maxima of the chemiluminescence intensity and pressure drop rate, showing the inertia of the thermocouple. Due to heterogeneous chain termination, which removes recombination energy, low pressures and a high heat removal rate, the process occurred in an almost isothermal mode. The time for which the maximum rate was reached, measured even after the induction period, is 0.4 s, which is thousands of times longer than the heat removal time. Since self-heating is insignificant and practically the same at both given temperatures, its contribution can be neglected when considering the ratio of chain reaction rates. According to the stoichiometry of the process

$${\text{2}}{{{\text{H}}}_{{\text{2}}}}{\text{ + }}{{{\text{O}}}_{{\text{2}}}}{\text{ = 2}}{{{\text{H}}}_{{\text{2}}}}{\text{O}}{\text{,}}$$

a decrease in the number of moles of the mixture is equal to a decrease in the number of moles of O2. Therefore, the ratio of the maximum values of the angular coefficients of kinetic curves 1 and 1' is equal to the ratio of the maximum rates of O2 consumption at 773 and 768 K. This ratio is 1.29; i.e., upon heating by 5°, the reaction rate increases by 29%. However, the increase in the rate constant for the limiting stage (I), equal to 1.87 × 1014 exp(–8350 K/T) cm3 mol–1 s–1 [19, 20, 34], with such an increase in temperature is only 7%. Thus, a significantly stronger temperature dependence of the reaction rate compared to the traditionally used Arrhenius law is manifested even with a temperature difference of only 5°.

As can be seen from Table 1.IX, the real increase in the reaction rate with increasing temperature is in good agreement with that calculated from Eq. (27.IX). The slight increase in the calculated rate ratio over time (second column) is due to the fact that the calculations neglected the O2 consumption and, accordingly, the calculated reaction rates increased slightly over time. The difference in the temperature dependences of the reaction rate and the quantity k1 makes it possible to determine the contribution of the increase in the CC concentration to the observed anomalous dependence of the reaction rate on temperature.

Let us express the temperature dependence of the reaction rate using the well-known equation

$${\text{ln}}({{W}_{2}}{\text{/}}{{W}_{1}}) = \frac{{E\left( {{{T}_{2}}-{{T}_{1}}} \right)}}{{R{{T}_{1}}{{T}_{2}}}},$$
(28.IX)

where W2 and W1 are the reaction rates at Т2 and Т1, Е is the effective activation energy, and R is the gas constant.

Substituting into this expression the ratio of the maximum slopes of the oscillograms in Fig. 5.IX, equal to 1.29, and the values of Т1 and Т2, we obtain the effective activation energy of the process, amounting to 251.4 kJ/mol. At the same time, the activation energy in the rate constant k1 is equal to only 70 kJ/mol [34, 30]. From these data and from the expression for the rate of O2 consumption,

$$W = -\frac{{{\text{d}}\left[ {{{{\text{O}}}_{2}}} \right]}}{{{\text{d}}t}} = {{k}_{1}}\left[ {\text{H}} \right]\left[ {{{{\text{O}}}_{2}}} \right],$$
(29.IX)

it is obvious that the difference between the above values of the activation energy of the process and the activation energy of the rate constant k1, equal to 181.4 kJ/mol, is determined by the temperature dependence of the rate of increase in the chain carrier concentrations.

Thus, with an increase in temperature even by only 5°, the contribution of the increase in the CC concentration to the acceleration of the chain process turns out to be much greater than the effect of the increase in the rate constant for the limiting stage, corresponding to the Arrhenius law. Thus, the experimental data, in agreement with what was said in Section 1, show that the temperature dependence of the combustion reaction rate is fundamentally different from the Arrhenius law and refute the previously generally accepted ideas about the correspondence of the rate dependence to this law. Since the temperature dependence of the reaction rate does not correspond to the Arrhenius law, the method of expanding the exponential in the equation of this law, proposed in [3], is not justified.

These results also make it possible to estimate the H atom concentration that ensures the observed reaction rate and the excess of its growth over the increase in the rate constant k1. Dividing the maximum value of \(W\) calculated from the pressure oscillogram by the corresponding O2 concentration (Fig. 5.IX), we obtain the H atom concentration at the moment of maximum reaction rate equal to 1.3 × 1014 atom/cm3. This value, together with the above activation energy of 181 kJ/mol, is in good agreement with the H atom concentration in the flame of the same mixture at 930 K and 3 Torr measured using EPR [48], which is close to 3 × 1015 atom/cm3. Indeed, from the given values of the H atom concentration and the activation energy, a concentration of these atoms at 930 K equal to 2.3 × 1015 atoms/cm3 is obtained. Thus, the conclusion of the theory about the determining role of the increase in the CC concentration in the temperature dependence of the reaction rate is confirmed quantitatively by the results of measurements of W, ΔT, and the H atom concentration.

The role of CCs in the reaction rate and its temperature dependence is even more significant at a larger temperature difference. Below we compare the rates of the H2 oxidation reaction at 843 K (the self-ignition temperature is about the third limit at 1 atm [36]) and at the temperature of flame propagation in the absence of an explosion, i.e., without adiabatic compression. The reaction rate given in [36] is 7.2 × 1015 molecule cm–3 s–1. At this rate, the characteristic reaction time is three orders of magnitude longer than the heat removal time. Therefore, self-heating is not detected.

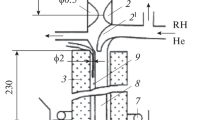
In [49], the combustion of a mixture of 15% H2 with air was performed in a molybdenum tube with a diameter of 1.2 cm and a length of 210 cm with an open end (Fig. 6.IX). Along the tube, photomultiplier tubes were placed, the signals of which were transmitted to a multichannel oscilloscope connected to a computer. To eliminate interference from extraneous light, the tube was wrapped in black paper. To reduce heterogeneous recombination, the tube was rinsed with boric acid. According to chromatographic analysis, hydrogen burns out almost completely. According to stoichiometry, the O2 consumption is twice smaller. The maximum possible (adiabatic) heating is 1070 K. Assuming a 15% loss, the heating is equal to 910 K. Accordingly, the flame temperature is 1203 K. The average reaction rate is equal to the ratio of the concentration of consumed O2 to the time the mixture is found in the flame zone. This time was determined as the quotient of the flame thickness and its speed. The flame speed, which was found from the slope of the х–t diagrams of the stationary flame path, was about 3 m/s. The width of the flame zone, close to 0.15 cm, was determined from the temperature profile along the flame, known for a given mixture composition [50]. This width at a given flame speed corresponds to a reaction duration of 5 × 10–4 s. It is worth noting that the observed rates are achieved without a noticeable increase in pressure, i.e., without adiabatic compression.

Fig. 6.
figure 6

IX. Reactor for studying flame propagation: (1) discharger, (2) oscilloscope, (3) photosensors, (4) reaction tube, (5) tap to pressure gauge, (6) pressure gauge, (7) valve to the pump, and (8) inlet pipe for gas intake.

Full size image

The average reaction rate is equal to the amount of O2 consumed divided by the time the mixture is found in the flame zone. Taking into account the initial H2 concentration at this temperature, which is 2.2 × 1017 molecule cm–3 s–1, the reaction duration is shorter than 5.10–4 s, we obtain the rate of the hydrogen combustion reaction exceeding 4 × 1020 molecule cm–3 s–1 and, accordingly, the rate for oxygen exceeding 2 × 1020 molecule cm–3 s –1. Thus, the extremal character of the reaction rate is manifested in the fact that, in less than 5 × 10–4 s, in each cm3, almost all 2.2 × 1017 strong H2 molecules and an equivalent amount of even stronger O2 molecules are consumed. Such self-accelerations and rates correspond to the law (20.IX).

Another manifestation of the extremal character of the reaction kinetics is its self-acceleration. At 843 K, the rate in a mixture of H2 and O2 is 7.2 × 1015 molecule cm–3 s–1 [36]. Given the corrections for differences in gas densities and initial compositions, the rate at 1203 K increases to 1022 molecule cm–3 s–1. This means that, when the temperature increases from 843 to 1203 K, the process accelerates 106-fold in ten-thousandths of a second. At the same time, the rate constant for reaction (I) with such an increase in temperature increases only 20-fold; i.e., the acceleration according to the Arrhenius law is 5 × 104 times smaller than the real one. There is almost no increase in pressure, since the end of the tube is open. The abrupt self-acceleration of reactions is discussed in the next chapter.

The conditional activation energy corresponding to the acceleration upon heating from 843 to 1203 K is 368 kJ/mol, which also reflects a special law of the temperature dependence of the reaction rate and refutes the hypothesis that the temperature dependence of the rate corresponds to the specified law concerning only the rate constant. Since the activation energy determined from the semi-logarithmic anamorphosis of the dependence of the reaction rate on the reciprocal temperature depends on the reaction conditions, it is quite obvious that the anamorphosis used does not correspond to the real process. For the same reason, the Zeldovich number is not a reaction parameter.

Since O2 is consumed only in the reaction with atomic hydrogen, the strong excess of the increase in W over the increase in k1 is caused by an increase in the H atom concentration. This means that the rate and acceleration of the reaction during flame propagation are determined almost exclusively by the increase in the concentration of active particles. Dividing the reaction rate by the O2 concentration and k1, we obtain, according to expression (29.IX), the H atom concentration in the flame equal to 8.8 × 1014 atom/cm3, which is 0.5% of [H2]. This value is close to that measured in the flame of mixtures of similar composition by mass spectrometry [50]. Thus, the observed flame speed of 3 m/s even in a hydrogen-poor mixture in an open-ended tube is realized due to extreme accelerations and reaction rates and high concentrations of H atoms multiplying according to the law (19.IX).

The characteristic reaction time during an explosion, defined as the ratio of the size of the flame cell and the speed of the blast wave, is a fraction of a microsecond. Such reaction rates correspond to H atom concentrations reaching whole percentages of the entire mixture. These phenomena are discussed in Chapter X.

The results presented above show that, in chain combustion processes, the reaction system provides the most rapid decrease in the Gibbs free energy G to achieve an equilibrium state. This is realized by creating, due to the enthalpy of the initial reagents, very high concentrations of free atoms and radicals, which, due to their free valences and the chain nature of the reactions, quickly react with the initial reagents, turning them into final products.