SYNTHESIS ON THE EXISTENCE/NON-EXISTENCE OF MULTIPLE SOLUTIONS FOR AN UNSTEADY NON-ROTATING SHRINKING DISK FLOW

Abstract

Results of studying the problem of an unsteady fluid flow along an instantaneously stretching (shrinking) non-rotating disk with an infinite radius are reported. The velocity of the shrinking disk surface is chosen in such a way that the problem allows the existence of an exact similarity solution. The original problem is reduced to an initial-value problem, which is solved numerically by using the shooting and Newton–Raphson methods. A detailed study of the existence and uniqueness of the solution is performed.

INTRODUCTION

In 1921, von Kármán [1] studied a classical fluid mechanics problem for a free rotating disk boundary layer flow. He used a similarity transformation in order to transform the well-known Navier–Stokes equations into coupled ordinary differential equations. In 1934, von Kármán’s work was extended by Cochran [2] who considered impulsive fluid motion started from rest. The flow between a stationary disk and a rotating disk was addressed by Mellor et al. [3]. An ample amount of literature can be cited regarding the rotating disk flow phenomenon, while quite a few attempts have been made to analyze the flow situations stimulated by a non-rotating disk.

Since the last one and half decade, the question of non-uniqueness of solutions of equations describing the flow on shrinking surfaces has been a topic of interest for a large part of the concerned community. This is a matter of fact that non-uniqueness of the solution of boundary-layer flows due to moving continuous surfaces was initially discovered for shrinking surface flows. Therefore, most of the subsequent studies in this direction paid particular attention to shrinking surface flows. It is now widely believed that non-uniqueness of the solution is a salient feature of shrinking sheet flows. It has repeatedly been reported by various researchers (see, e.g., [4–8]) that shrinking surface flows admit a non-unique solution, while stretching surface flows admit a unique solution. It was recently demonstrated [9–12] that the existence of a non-unique solution is not a particular feature of shrinking surface flows only. Instead, this can equally be observed for stretching surface flows as well.

A detailed analysis of the two-dimensional case of stretching/shrinking sheet flows was performed in [9, 10]. In that study, it was also shown that the duality of the solution is also possible for a stretching sheet flow and a unique solution can also be obtained for a shrinking sheet flow. The two-dimensional axisymmetric case of a stretching/shrinking cylinder was reported in [11, 12]. In those studies, it was shown that multiple solutions are possible for flows past both stretching and shrinking cylinder cases.

However, the axisymmetric case of a non-rotating stretching/shrinking disk has not been given significant attention.

In the current study, we consider an unsteady flow past a stretching/shrinking disk with accelerated and decelerated flow situations. The question of existence of a unique or non-unique solution is explored in this study by justifying the observed facts against experimental data.

1. FORMULATION OF THE PROBLEM

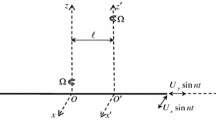
Consider a circular flat disk of an infinite radius immersed in a viscous fluid. The disk is flexible in nature so that radial stretching/shrinking with a velocity $u_w(r,t)$ is possible. In order to allow for a normal wall velocity across the disk surface, the disk is assumed to be porous. The pores are assumed to be identical and homogeneously distributed over the entire disk surface. An axisymmetric two-dimensional unsteady flow is formed due to disk stretching/shrinking. The flow geometry and the associated coordinate system are shown in Fig. 1.

Fig. 1

Flow geometry and associated coordinate system.

Because of the symmetry of the flow on both sides of the disk, we prefer to consider the upper half domain for our further analysis. Owing to the axisymmetric nature of the disk and the flow, the governing equations (in cylindrical coordinates) after the implementation of the boundary-layer assumptions are written as

$$ \frac{\partial\,(ru)}{\partial r}+\frac{\partial\,(rw)}{\partial z}=0;$$

(1)

$$ \frac{\partial u}{\partial t}+u\,\frac{\partial u}{\partial r} +w\,\frac{\partial u}{\partial z}=\nu\,\frac{\partial^2u}{\partial z^2}.$$

(2)

The initial and boundary conditions for this system are

$$t=0{:}\qquad u(r,z,t)=0\quad \forall\ r,z,$$

$$ z=0{:}\qquad u=u_w(r,t),\quad w=w_w(r,t),$$

(3)

$$z=\infty{:}\qquad u=0.$$

Here $u$ and $w$ are the velocity components taken along the radial and axial directions, respectively, $\nu$ is the kinematic viscosity, and $w_w(r,t)$ is the suction or injection velocity. System (1)–(3) admits an exact similarity solution if the wall velocity follows the law

$$ u_w(r,\tau)=\bar{a}r/\tau\qquad(\tau =|\bar{a}|t)$$

(4)

or

$$ u_w(r,t)=\bar{a}r/(1-\gamma t),$$

(5)

where $\bar{a}$ is a dimensionless constant with the dimension inverse to time, which denotes the uniform stretching/shrinking velocity $\nu e$ ($-\nu e$), and $\gamma$ is a constant with the dimension inverse to time ($\gamma>0$ and $\gamma<0$ refer to accelerated and decelerated motion of points on the disk surface). To ensure similarity for the wall stretching/shrinking velocities (4) and (5), the suction/injection velocity must be described as

$$w_w(r,\tau)=d\tau^{-1/2},\qquad w_w(r,\tau)=d/\sqrt{1-\gamma t},$$

where $d$ is a constant with the dimension of velocity ($d>0$ and $d<0$ correspond to injection and suction velocities, respectively).

The dimensionless similarity transformations of this flow have the form

$$ \eta =\sqrt{\pm\frac{u_w(r,t)}{\nu r}}\,z,\qquad u=u_w(r,t)f'(\eta),\qquad w=\pm \Big(-2\sqrt{\pm\frac{u_w(r,t)\nu}{r}}\,\Big)f(\eta).$$

(6)

The plus and minus signs refer to the stretching and shrinking nature of the disk, respectively, $f(\eta)$ denotes the dimensionless stream function $\psi (r,z,t)$, and the velocity components $u$ and $w$ are expressed via the stream function as

$$u=\frac{1}{r}\,\frac{\partial\,(r\psi )}{\partial z},\qquad w=-\frac{1}{r}\,\frac{\partial\,(r\psi )}{\partial r}.$$

As a result, the continuity equation (1) is satisfied identically.

Under the action of the similarity transformations (6), the momentum equation (2) and the associated initial and boundary conditions transform to the equivalent equations

$$ f'''=2ff''-f^{\prime2}+\beta (f'+\eta f''/2);$$

(7)

$$ f(0)=1,\qquad f(0)=S,\qquad f'(\infty)=0.$$

(8)

The velocity $u_w$ involved into Eq. (6) is obtained from Eq. (5) after the substitution $\bar{a}=-a$ ($a>0$). Therefore, the parameter $u_w$ represents the shrinking wall velocity. The parameter $\beta =\gamma/a$ is termed as the unsteadiness parameter, and its positive and negative values correspond to accelerated and decelerated flow situations, respectively. The existence of multiple solutions was quite assured in the decelerated case [9–12]. Moreover, for $\beta =0$, the case of a steady linearly stretching/shrinking disk is recovered. The negative and positive values of the suction/injection parameter $S=d/(2\sqrt{|a|\nu}\,)$ characterize the wall suction or injection situations, respectively.

Due to the similarity transformations (6), which involve the velocity $u_w$ defined in Eq. (4), the momentum equation is transformed to

$$ f'''=2(f-\eta/4)f''-(1+f')f',$$

(9)

whereby the transformed boundary conditions have the form of Eq. (8). Interestingly, Eq. (9) is a special case of Eq. (7) and is readily recovered from Eq. (7) at $\beta =-1$. Therefore, it is preferable to consider system (7), (8), where the solution for the wall velocity $u_w$ given in Eq. (4) is obtained for $\beta =-1$. The coefficient of the wall skin friction is defined as

$$C_f=\frac{\tau_w}{\rho u_w^2/2},$$

where the wall shear stress $\tau_w$ is given by

$$\tau_w=\frac{\partial u}{\partial z}\Big|_{z=0}.$$

With the use of Eqs. (5) and (6), one obtains

$$C_f=-\mathrm{Re}_x^{-1/2}f''(0),$$

where $\mathrm{Re}_x=\sqrt{u_w r/(4\nu)}$ is the Reynolds number.

2. SOLUTION PROCEDURE

The goal of the present study is to consider situations where multiple solutions are possible and to find these solutions. The MATHEMATICA software is used here, which includes a computer code based on the 4th-order Runge–Kutta shooting technique. In the framework of the Runge–Kutta method, it is desirable to transform the governing ordinary differential equations to a system of the first-order ordinary differential equations. Consequently, the boundary-value problem is transformed to an initial-value problem. This initial-value problem is then solved numerically by marching in the $\eta$ direction. The procedure is iterated several times until the outer boundary condition is satisfied. Problem (7), (8) is reduced to the following system of the first-order differential equations:

$$ y'_2=2yy_2-y_1^2+\beta(y_1+\eta y_2/2),\qquad y_1'=y_2,\qquad y'=y_1$$

(10)

[$y=f(\eta)$]. The associated initial conditions are

$$ y_1(0)=1,\qquad y(0)=S,\qquad y_2(0)=\xi.$$

(11)

To figure out a numerical solution of the initial-value problem (11), (12), we use the shooting method. In this method, the prime task is to sort out the missing condition, i.e., $y_2(0)=\xi$, which is searched out by taking an appropriate step size $\xi$ as well as a suitable infinity interval that make the solution satisfy the outer boundary condition $y_1(\infty)=0$. In this regard, the Newton–Raphson method is adopted to attain the desired accuracy. To numerically satisfy this condition, it is implemented that the iterative process will stop when $y_1(\infty)=0.001$. This method enabled us to trace out not only the first solution, but also the second solution with desired accuracy.

Usually, the first solution is captured quite easily, while capturing the second or third solution is quite tricky and laborious. It involves several manipulations with the initial guess and the domain of the solution. To ensure the accuracy and validity of our computing code, already existing results [10, 13] are reproduced; and comparisons are performed in Table 1. Obviously, excellent agreement is achieved, which validates the accuracy of our current numerical code.

Table 1. Solutions obtained in the present study and in [10, 13]

Fig. 2

Wall skin friction coefficient $f''(0)$ versus $S$ for various values of $\beta$: (a) $S=-3.0$ to $-1.4$; (b) $S=-1.42$ to $-1.35$; the solid and dashed curves show the first and second solutions, respectively, for $\beta=-5$ (1), $-4$ (2), $-3$ (3), $-2$ (4), and $-1$ (5).

3. RESULTS AND DISCUSSION

The solution is obtained for various values of the unsteadiness parameter $\beta$ and suction/injection parameter $S$.

It is observed that, for an unsteady shrinking disk flow, a solution is possible neither in the presence of the wall injection phenomenon nor in the absence of the wall suction phenomenon. That is, a solution is only possible in the presence of a sufficient wall suction velocity. For this reason, we recognize $S$ only as a suction parameter in the subsequent discussion. Duality of the solution is captured for some chosen values of $\beta <0$ and $S<0$. For $\beta>0$, no duality of the solution is seen to the best of our efforts.

Figures 2 and 3 show the wall skin friction coefficient versus $S$ for various values of $\beta$ and versus $\beta$ for various values of $S$, respectively.

Fig. 3

Wall skin friction coefficient $f''(0)$ versus$\beta$ for various values of $S$: (a) small absolute values of $S$ [$S=-1.50$ (1), $1.40$ (2), $-1.38$ (3), $-1.36$ (4), and $-1.35$ (5)]; (b) moderate absolute values of $S$ [$S=-10$ (1), $-8$ (2), $-6$ (3), $-4$ (4), and $-2$ (5)]; (c) large absolute values of $S$ [$S=-30$ (1), $-25$ (2), $-20$ (3), and $-15$ (4)]; the solid and dashed curves refer to the first and second solutions, respectively.

Table 2. Numerical values of $S_{\rm cr}$ for various values of $\beta$

Figure 2 depicts an interesting and important observation regarding the existence of the solution in the decelerated flow $\beta <0$. Obviously, the solution never exists in the wall injection case and is conditionally existent in the wall suction case with the requirement of a sufficient wall suction velocity. The critical values $S_{\rm cr}$ of the parameter $S$ at which the solution starts to exist and where two solution branches join each other are reported in Table 2. Similarly, for a certain chosen value of $S$, it is possible to find an interval of $\beta$ where the solution exists. In Fig. 3a, the wall skin friction coefficient is plotted against $\beta$ for some chosen values of $S$ having relatively small absolute values. Obviously, for each such chosen value of $S$, the solution is existent for a certain interval of $\beta$. As the magnitude of $\beta$ increases, the two solutions intend to join each other (this behavior is, however, limited to curves corresponding to small absolute values of $S$ and does not apply to all curves), and the solution is non-existent for greater values of $\beta$. This is because, for a given/chosen wall suction velocity, the solution can be supported only for a certain level of flow retardation. Therefore, at the further retarded stages (corresponding to increasing $\beta$), the solution seizes to exist. The critical values $\beta_{\rm cr}$ of the parameter $\beta$ at which two solutions join each other are listed in Table 3.

Table 3. Values of $\beta_{\rm cr}$ for various values of $S$

Fig. 4

Flow velocity versus $\eta$ for $\beta =-1$ and various values of the suction parameter $S$: $S=-10$ (1), $-8$ (2), $-6$ (3), $-4$ (4), and $-2$ (5); the solid and dashed curves refer to the first and second solutions, respectively.

At this point, it is important to remark that duality of the solution is actually connected to situations where the flow becomes retarded and requires some support either with the provision of some wall suction, or with the provision of a favorable pressure gradient, or due to the presence of transverse surface curvature (see, e.g., [9–12]). In Fig. 3b, similar results are reported for some relatively large magnitudes of $S$ versus $\beta$ ($\beta>0$). The second solution grows rapidly and takes large values; therefore, it is not shown completely. As the suction velocity becomes sufficiently large, the second solution vanishes for sufficiently small magnitudes of $\beta$ (cf. Figs. 3a and 3b). Obviously, the second solution exists for $S=-1.40$, $-1.38$, $-1.36$, and $-1.35$ for all $\beta <0$; however, at $S=-1.50$, the second solution seized to exist in the interval $-1<\beta <0$. Interestingly, with a further increase in $S$, the interval of $\beta$ for which the solution exists gradually extends to the right (cf. Figs. 3b and 3c).

Fig. 5

Flow velocity versus $\eta$ for $S=-5$ and various values of the flow unsteadiness parameter $\beta$: $\beta=-5$ (1), $-4$ (2), $-3$ (3), $-2$ (4), and $-1$ (5); the solid and dashed curves refer to the first and second solutions, respectively.

Figures 4 and 5 show the flow velocity $f'$ as a function of the parameter $\eta$ for various values of the parameters $S$ and $\beta$.

The effect of wall suction on the first solution is to reduce the boundary-layer thickness, which is a well-known fact. However, the effect of the unsteadiness parameter $\beta$ on the velocity profile in this case is very small (see Fig. 5). The second solution is significantly affected by both $S$ and $\beta$.

CONCLUSIONS

In this study, an unsteady flow due to an impulsively started shrinking disk is considered. The shrinking wall velocity is chosen in such a way that an exact similarity solution is possible. The problem under consideration can be divided into two cases: accelerated case ($\beta >0$) and decelerated case ($\beta <0$). A steady solution for a linearly shrinking disk is recovered at $\beta =0$. It is observed that the solution in the accelerated case ($\beta >0$) is unique and requires a sufficient wall suction velocity for its existence. In the retarded case ($\beta <0$), the solution is non-existent (in general) without wall suction and also requires sufficient wall suction for its existence. For moderate suction velocities, the duality of the solution is observed for $\beta <0$; if the suction velocity is sufficiently large, the domain of duality of the solution $\beta$ further shrinks to $\beta \le -1$. Hence, it is concluded that the non-uniqueness of the solution is actually due to the retarded nature of the flow. Whenever the flow is retarded, a non-unique solution is likely to exist, and it may require a supporting agent, such as a favorable pressure gradient, or transverse surface curvature, or wall suction, etc., for its existence.