ANALYSIS OF THE TURBULENT BOUNDARY LAYER AND SKIN-FRICTION DRAG REDUCTION OF A FLAT PLATE BY USING THE MICRO-BLOWING TECHNIQUE

Abstract

Numerical analyses of turbulent boundary layer parameters and skin-friction drag reduction on a flat plate under the effect of air micro-blowing with the use of the SST $k{-}\omega$ turbulence model are performed. The macroscale characteristics of a huge number of microjets are simulated by using a microporous wall model (MPWM) incorporated into ANSYS FLUENT by user-defined functions. Numerical results obtained within the Mach number range $\text{M}=0.2{-}0.5$ (Reynolds number $\mathrm{Re}=2.88\cdot 10^6{-}7.20\cdot 10^6$) confirm the experimental data of other researchers. Furthermore, a slight increase in the boundary layer thickness, displacement thickness, and momentum thickness, as well as a decrease in the velocity gradient and shear friction are well captured. In comparison to a simple flat plate, applying air micro-blowing reduces the skin-friction coefficient by 51% at the Mach number $\text{M}=0.4$ and blowing fraction of 0.008. Additionally, the skin-friction coefficient decreases as the blowing fraction and Mach number increase.

INTRODUCTION

Reducing energy consumption in flow processes is one of the greatest challenges for mechanical engineers nowadays. Hence, active and passive methods, such as uniform blowing/suction [1–4], plasma actuators [5, 6], passive vortex generator [7], and surface waves [8], are developed for reducing the drag penalty in many industries such as aviation [9, 10] and high-speed trains [11]. Micro-blowing [12] and an unsteady jet [13] are also kinds of active flow control (fluid) methods for reducing the skin-friction drag or controlling the flow separation, respectively.

The boundary layer equations for an incompressible fluid in motion past a flat plate were studied numerically and analytically by Catherall et al. [14]. In the case of uniform injection of the fluid from the plate, the viscous boundary layer was found to be displaced, which made the high-velocity flow separate from the wall of the plate. Catherall et al. [14] also found that fluid injection accelerates flow separation, especially for large blowing rates. Çuhadaroğlu et al. [15] examined experimentally uniform injection through a perforated surface of a square cylinder. In their study, the rate of injection and the location of the porous plate were varied, and the effect of injection on the pressure and drag coefficients was investigated. They found that injection of air is an effective way to influence the characteristics of a turbulent boundary layer. In addition, as a consequence of blowing, the boundary layer was found to be thicker, thereby decreasing the gradient of velocity at the wall and reducing the drag coefficient.

Creating surfaces with smaller holes is more accessible than before with the advent of laser drilling. Thus, air injection through holes with micrometer-order diameters became possible. Numerous works on air blowing through these much smaller holes were presented at the NASA Glenn Research Center in Cleveland, Ohio. To make a difference from injection through larger holes that was studied in the past, the word “micro-blowing" (MB) was used for air blowing through a microporous plate. Hwang [16] presented a concept for skin-friction reduction by using the micro-blowing technique (MBT) in subsonic flows. He performed experiments with five porous plates and measured the ratio of skin-friction coefficients to that of a solid flat plate for each test plate. The results showed that skin-friction reduction for the PN2 plate is approximately 60% with the maximum blowing rate of 0.205 kg/(m$^2\,\cdot\,$s) at a Mach number of 0.3. After that, Kornilov and Boiko [17] studied experimentally the efficiency of air micro-blowing through a wall consisting of alternating permeable and impermeable sections to reduce the turbulent skin-friction drag of a flat plate in a nominally gradientless incompressible flow. They found that micro-blowing with the same airflow rate as that at a completely permeable surface can provide flat-plate total drag reduction of about 15–25%.

Moreover, Kornilov and Boiko [18] found that consistent reduction of the local skin-friction coefficient over the microporous plate can reach a maximum value of 70%. They also worked on the application of air micro-blowing through a porous wall for skin-friction reduction on a flat plate [19]. A comprehensive and useful review of the topic was provided by Kornilov [20].

The numerical analysis of the MBT by tools of computational fluid dynamics (CFD) had been difficult before the presentation of the microporous wall model (MPWM) by Li et al. [21]. This difficulty comes from the massive number of microchannels in the MBT porous plate that should be simulated regardless of still limited computing capability. A numerical investigation on MBT applications was performed for a supercritical airfoil by Gao et al. [22]. Their results indicated that the maximum skin-friction drag reduction could be attained when the MBT was applied near the leading edge of the airfoil. In addition, with a blowing fraction of 0.05, a decrease in the total drag by 12.8–16.8% and an increase in the total lift by 14.7–17.8% could be attained.

Shkvar et al. [23] studied the efficiency of micro-blowing for the external surface of high-speed trains. They declared that micro-blowing seems to be the most effective, reasonable, and practically applicable method among the rest of known turbulent flow control technologies in the case of its application to high-speed trains due to the following advantages: it does not influence the motion stability and cannot lead to flow separation; it effectively acts, first of all, on the friction drag (reduces it up to 90%), which is the most significant drag component for very long bodies like a train; finally, the effects of compressibility (in particular, the emergence of shock waves) typical for aircraft’s cruising flight are not significant and do not need to be accounted for the train as negative factors.

Recently, Xie et al. [24] used direct numerical simulation to investigate the turbulent flat plate boundary layer with localized micro-blowing. The results showed that the drag reduction is efficient, and the local maximum rate of drag reduction can reach 40%. Meanwhile, visualization of a three-dimensional vortex displayed several concave marks on the surface of the near-wall vortices, which is caused by micro-jets. In addition, the effect of uniform micro-blowing was experimentally studied using stereo particle image velocimetry (SPIV) measurements in a zero pressure gradient turbulent boundary layer by Hasanuzzaman et al. [25]. They found that the boundary layer is strongly affected by micro-blowing. Moreover, the results showed that the momentum thickness and shape factor increase with increasing blowing ratio.

In the present research, a numerical analysis of a turbulent flow over a flat plate with air blowing through the microporous plate for drag reduction purposes was performed. The SST $k{-}\omega$ turbulence model was used for simulating the turbulent flow. Air micro-blowing through the microporous plate was simulated by considering the MPWM as the macroscale characteristics of the huge number of microjets.

1. PHYSICAL AND MATHEMATICAL DESCRIPTION

The problem formulation is described below, and the model of skin friction on a flat plate is studied.

1.1. Computational Domain

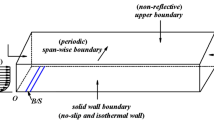
Based on the experimental study of Hwang [16], a two-dimensional rectangular computational domain was considered with 63.5 cm in length and 30 cm in height. In addition, a microporous plate 25.4 cm long was placed at a distance of 38.1 cm downstream from the flow inlet (Fig. 1).

Fig. 1

Domain of the present study: (1) wall; (2) microporous plate.

1.2. Microporous Wall Model

In this research, NASA-PN2 from [16] was selected as a microporous plate. The plate thickness was 1.02 mm, its porosity was 23%, and the hole diameter was 0.165 mm. The structure of the microporous plate is illustrated in Fig. 2. As can be seen in this figure, there is a gap between the two porous layers, which is called a cavity.

Fig. 2

Structure of the microporous plate [16]: (1) transverse flow; (2) micro-blowing; (3) cavity; (4) blowing air supply; (a) top view; (b) side view.

As mentioned before, the MPWM is used to apply the effects of air blowing through the microporous plate. In this model, the microporous plate is simplified into a type of boundary conditions to represent the macroscale features of a huge number of microjets. The averaged blowing velocity through the microporous plate can be calculated by the following formula [22]:

$$v_\mathrm{MB}=\varphi F\,\frac{\rho_\infty U_\infty}{\rho_\mathrm{ ex}}.$$

Here $U_\infty$ is the free-stream velocity and $F$ is the blowing fraction calculated as

$$F=\frac{\rho_\mathrm{ ex}U_j}{\rho_\infty U_\infty},$$

 $\varphi$ is the porosity of the NASA-PN2 microporous plate, $\rho_\mathrm{ ex}$ is the local density at the wall of the microporous plate, and $U_j$ is the average blowing velocity through one micropore channel. It should be noted that $U_j\neq v_\mathrm{MB}$ and $v_\mathrm{MB}=\varphi U_j$. Here $U_j$ is calculated by the formula

$$U_j=F\,\frac{\rho_\infty U_\infty}{\rho_\mathrm{ ex}}.$$

1.3. Governing Equations

In this research, the flow is two-dimensional, steady, and compressible. Air is considered as an ideal gas. The energy equation is used. The Reynolds-averaged Navier–Stokes (RANS) equations are written in the following form [26]:

—Continuity equation

$$\frac{\partial \bar{u}_i}{\partial x_i}=S_m,$$

where $S_m$ is the mass source;

—Momentum equation

$$\rho \bar{u}_j\,\frac{\partial\bar{u}_i}{\partial x_j} =-\frac{\partial\bar P}{\partial x_i}+\frac{\partial}{\partial x_j} \Big(\mu\,\frac{\partial\bar{u}_i}{\partial x_j} -\rho\,\overline{u'_iu'_j}\,\Big)+F_i,$$

where

$$-\rho\,\overline{u'_iu'_j}=\mu_t\Big(\frac{\partial\bar u_i}{\partial x_j} +\frac{\partial\bar u_j}{\partial x_i}\Big) -\frac{2}{3}\,\rho k\delta_{ij},$$

 $\rho$ is the density, $P$ is the pressure, $\mu$ is the dynamic viscosity, $\mu_t$ is the turbulent dynamic viscosity, $F_i$ is the momentum source, $k$ is the turbulent kinetic energy, and $\delta_{ij}$ is the Kronecker symbol;

—Energy equation

$$\rho C_p\bar{u}_i\,\frac{\partial\bar T}{\partial x_i} =\frac{\partial}{\partial x_j}\,\Big[\Big(K+\frac{C_p\mu_t}{\text{Pr}_t}\Big) \frac{\partial\bar T}{\partial x_j}+\bar{u}_i(\tau_{ij})_\mathrm{eff}\Big],$$

where $C_p$ is the heat capacity, $T$ is the temperature, $K$ is the thermal conductivity, $\text{Pr}_t$ is the turbulent Prandtl number, and $(\tau_{ij})_\mathrm{eff}$ is the viscous dissipation:

$$(\tau_{ij})_\mathrm{eff}=\mu_\mathrm{eff}\Big( \frac{\partial \bar u_j}{\partial x_i} +\frac{\partial \bar u_i}{\partial x_j}\Big).$$

For the turbulent flow over the flat plate, the two-equation SST $k{-}\omega$ model [27] was used. The transport equations in Menter’s shear stress turbulence model can be calculated as

$$\frac{\partial}{\partial x_i}\,(\rho ku_i) =\frac{\partial}{\partial x_i}\Big[\Big(\mu+\frac{\mu_t}{\sigma_k}\Big) \frac{\partial k}{\partial x_i}\Big]+\tilde{G}_k -\rho \beta^*k\omega,$$

$$\frac{\partial}{\partial x_i}\,(\rho\omega u_i) =\frac{\partial}{\partial x_i}\Big[\Big(\mu+\frac{\mu_t}{\sigma_\omega}\Big) \frac{\partial\omega}{\partial x_i}\Big] +\frac{\alpha}{v_t}\,\tilde{G}_k-\rho \beta \omega^2+D_\omega,$$

where $\tilde{G}_k$ represents the production of turbulent kinetic energy due to the mean velocity gradients:

$$\mu_t=\frac{\rho k}{\omega }\,\frac{1}{\max\,[1/\alpha^*,SF_2/(a_1\omega)]},\qquad \tilde{G}_k=\min\,(G_k,10\rho \beta^*k\omega),\qquad G_k=-\rho\,\overline{u'_iu'_j}\,\frac{\partial\bar u_j}{\partial x_i},$$

$$D_{\omega }=2(1-F_1)\rho\,\frac{1}{\omega\sigma_{\omega ,2}}\, \frac{\partial k}{\partial x_j}\, \frac{\partial\omega }{\partial x_j}.$$

More information on these equations can be found in [27].

In the wall boundary conditions of this turbulence model, the turbulent kinetic energy equation is solved in the same way as the enhanced wall treatment method in the $k{-}\varepsilon$ model. This means that appropriate low-Reynolds-number boundary conditions should be applied for fine meshes near the wall. The value of $\omega$ is calculated by the equation [27]

$$\omega_w=\frac{\rho (u^*)^2}{\mu}\,\omega^+.$$

1.4. Boundary Conditions

The far-field Riemann boundary condition was imposed on the inlet boundary (along the left and upper sides of the domain). The free-stream Mach number was $\text{M}= 0.4$ and the Reynolds number was $5.76\cdot 10^6$ based on the 63.5 cm length of the flat plate. The pressure outlet boundary condition (right side of the domain) was fixed with a specified static pressure (1 atm), and the no-slip wall condition was adopted for the flat plate surface. To apply air blowing through the microporous plate as a boundary condition, the mass flow and momentum sources were added into the governing equations for the first layer of cells adjacent to the microporous plate.

2. COMPUTATIONAL METHOD

In this paper, the numerical calculation was performed with the ANSYS FLUENT software. A pressure-based coupled algorithm was used to solve a coupled system of equations by the finite volume method. Moreover, second-order schemes were used to calculate the cell face pressure and to discretize all equations. Moreover, to help in stabilizing the simulation and ensure faster convergence, the pseudo-transient under-relaxation method was applied. In all numerical simulations, the parameter $y^+$ had a value smaller than unity (Fig. 3).

Fig. 3

Variation of the parameter $y^+$ along the flat plate (the microporous part is the last 40% of the total length of the flat plate) for $\text{M}=0.4$ and $F=0.003$.

Fig. 4

Computational grid.

3. NUMERICAL CALCULATION

In the current study, all computational grids were generated by using a multi-block scheme with hexahedral elements (Fig. 4).

Table 1. Skin-friction coefficient for $\text{M}=0.4$ in the flat plate region $x= 0.381{-}0.635$ m

Table 2. Calculated and experimental values of the skin-friction coefficient for $\text{M}= 0.4$

Table 1 shows the skin-friction coefficients $C_f$ calculated on four grids by means of averaging along the microporous plate in accordance with the equation

$$C_f=\frac{1}{L}\int\limits^{L_2}_{L_1} \frac{\tau_w}{\rho U^2_\infty/2}\,dx,$$

where $\tau_w$ is the shear stress on the wall.

As shown in Table 1, the average skin-friction coefficient remains nearly constant if the number of computational cells exceeds 74 451. Therefore, this grid was used in all numerical simulations.

To validate the computational model, the numerical results obtained were compared with the experimental data of Hwang [28] and the numerical results of Gao et al. [22]. For $\text{M} =0.4$, Table 2 shows the ratio of the skin-friction coefficient of the flat plate with air micro-blowing to that without MBT. It should be noted that the skin-friction coefficient was averaged along the microporous plate in the region $x= 0.381{-}0.635$ m. The numerical results of this study are seen to be in acceptable agreement with the experimental data and previous numerical results [22]; the differences are 0.04–5.90% and 0.35–7.50%, respectively.

RESULTS AND DISCUSSION

The computed velocity profiles along the wall-normal direction for both cases, without MBT and with MBT at the blowing fraction $F=0.003$, are illustrated in Fig. 5.

Fig. 5

Wall-normal velocity profiles without micro-blowing (curve 1) and with micro-blowing ($F=0.003$) for $\text{M}=0.4$ (curve 2): $x=0.35$ (a), 0.40 (b), 0.45 (c), 0.50 (d), 0.55 (e), and 0.60 m (f).

Air blowing through the microporous plate was applied in the region $x=0.381{-}0.635$ m on the flat plate. The boundary layer thickness starts to increase at about $x\approx 0.4$ m. The differences in two velocity profiles increase as the flow passes over the microporous portion of the wall. Thus, the streamlines in the boundary layer can flow more smoothly over the surface covered with a thin layer of air. Therefore, micro-blowing can diminish the surface roughness. As a result, this thin layer of air can be considered as a slip flow on the surface. The MBT reduces the gradient of the velocity profile $(\partial u/\partial y)|_{y=0}$ on the flat plate surface, which causes a decrease in viscous shear friction.

Fig. 6

Velocity vectors near the wall of the microporous flat plate for various values of $x$ ($\text{M}=0.4$): $x=0.4$ (a), 0.5 (b), and 0.6 m (c); $F=0.003$ (1) and 0.008 (2).

By observing Fig. 6, which provides a qualitative representation of the velocity field, it can also be noted that the blowing fraction considerably affects the velocity profiles in the boundary layer (including the viscous sublayer) in the region where micro-blowing is applied. Air blowing through the microporous plate changes the velocity direction by making it more vertical, which ultimately results in the viscous drag decrease. It can also be noticed that the adopted computational approach does not produce any sudden jumps or singularities inside the computational domain. The flow remains smooth and its physicality is well represented.

To analyze the modified boundary layer thickness after applying the MBT, the displacement thickness $\delta^*$ and momentum thickness $\theta$ were determined as

$$\delta^*=\int\limits^\delta_0\Big(1-\frac{\rho u}{\rho_\infty U_\infty}\Big)\,dy,\qquad\theta =\int\limits^\delta_0\frac{\rho u}{\rho_\infty U_\infty} \Big(1-\frac{u}{U_\infty}\Big)\,dy,$$

where $\delta$, $\rho_\infty$, and $U_\infty$ are the boundary layer thickness, density, and free-stream velocity, respectively.

Fig. 7

Distributions of the boundary layer displacement thickness (a) and momentum thickness (b) along the coordinate $x/c$ for $\text{M}=0.4$ and various blowing fractions: $F=0$ (1), 0.003 (2), and 0.008 (3).

Figure 7 displays the variation of the displacement thickness and momentum thickness along the flat plate surface for various blowing fractions ($c$ is the flat plate length). As it follows from Fig. 7a, micro-blowing control has almost no effect on the upstream turbulent flow (downstream from the point with the coordinate $x/c= 0.6$); the displacement thickness and momentum thickness are equal to those without micro-blowing control. With air blowing through the microporous plate, the displacement thickness increases starting from the normalized coordinate $x/c\ge 0.6$; moreover, the larger the blowing fraction value, the greater the displacement thickness. This result can be seen in Fig. 5, where the boundary layer starts to grow when the MBT is applied and the blowing fraction starts to increase. Thus, all these results indicate that the boundary layer thickness increases slightly as a result of micro-blowing.

For $F = 0.003$ and 0.008, the displacement thickness increases along the microporous part, which indicates that the streamwise velocity within the boundary layer is lower than the free-stream velocity. Also, with micro-blowing control, the momentum thickness decreases. Furthermore, the skin-friction coefficient also decreases as a result of velocity reduction (Table 3).

Table 3. Skin-friction coefficients on the flat plate in the case with micro-blowing

The momentum thickness $\theta$ denotes the variation in the momentum inside the boundary layer. A large momentum thickness indicates that more momentum is gone. The momentum thickness $\theta$ increases with increasing blowing fraction at about $x/c>0.6$. It is clear that air micro-blowing induces a momentum loss and raises the momentum thickness.

Table 3 shows the ratios of the skin-friction coefficients on the flat plate with and without MBT. The results illustrate that the skin-friction coefficient decreases if the MBT is applied on the flat plate. Moreover, it can be seen that for both Mach numbers, $\text{M}=0.3$ and $\text{M} =0.4$, that the skin-friction coefficient decreases with an increase in the blowing fraction. This is due to the fact that the velocity gradient is reduced by air blowing through the microporous plate.

The results show that air micro-blowing in the case with $\text{M}=0.4$ (Re = $5.76\cdot 10^6$) and blowing fraction of 0.008 can reduce the skin-friction coefficient by 51% as compared to the value of $C_f$ in the flow past the flat plate without micro-blowing.

Fig. 8

Distributions of local values of the skin-friction coefficient along the flat plate for $\text{M}=0.4$: $F=0.003$ (1) and 0.008 (2).

Figure 8 illustrates the computed skin-friction distributions in the streamwise direction along the flat plate for two different blowing fractions, $F = 0.003$ and 0.008. As before, it can immediately be noted that the applied micro-blowing does not significantly affect the upstream flow. Mostly all the flow changes become visible in the region $x/c>0.6$. The greatest part of skin-friction reduction happens immediately after the MBT is applied, but this favorable trend also persists along the entire remaining part of the plate. At $\text{M} = 0.4$ and $F=0.008$, considerably greater skin-friction reduction is provided.

Fig. 9

Skin-friction coefficient versus the Mach number: $F=0.0015$ (1), 0.003 (2), 0.006 (3), and 0.008 (4).

The ratio of the skin-friction coefficients on the flat plate with and without the MBT as a function of the Mach numbers is plotted in Fig. 9. With increasing Mach number, skin-friction coefficient reduction on the flat plate with micro-blowing is more pronounced. Moreover, with increasing blowing fraction, the reduction of skin-friction coefficient is further enhanced. Therefore, the skin-friction coefficient on the flat plate can be reduced by increasing the Mach number and blowing fraction.

CONCLUSIONS

A numerical investigation was performed to analyze the turbulent boundary layer and skin-friction drag reduction of the flat plate by using the micro-blowing technique. The SST $k{-}\omega$ turbulence model was used to simulate the turbulent flow over the flat plate. The microporous wall model was applied to represent the macroscale characteristics of the huge number of microjets on the microporous plate. The numerical results of the turbulent flow by using the MPWM have reasonable conformity with the available experimental data and previous numerical studies.

In the case with micro-blowing control, the boundary layer thickness was found to increase. A greater value of the blowing fraction increases the intensity of the normal component of velocity adjacent to the wall surface, which instigates a decrease in the velocity profile gradient and, thus, the overall reduction of the viscous drag.

It was observed that the displacement thickness and momentum thickness increase owing to the MBT; moreover, the larger the blowing fraction, the greater the displacement thickness. The numerical results demonstrated that air blowing induces a momentum loss and increases the momentum thickness. In addition, the skin-friction coefficient decreases when the MBT is applied on the flat plate.