INTRODUCTION

The assumption of smooth surfaces of contacting bodies is used in classical formulations of contact problems. However, in practice, all bodies have a microrelief, so that contact occurs in discrete areas (real contact areas), rather than over the entire nominally flat region of interaction. Many important characteristics of tribocouplings, such as friction force, rigidity of couplings, electrical and thermal conductivities, and wear rate, depend on the real area of contact interaction. Therefore, accounting for the surface microrelief is of great practical significance.

At present, various numerical and analytical approaches have been developed to solve contact problems for elastic bodies taking into account the microgeometry of the contacting surfaces. However, studies of contact problems for viscoelastic bodies taking into account the roughness of their surfaces are few in number, despite the importance of considering the relaxation properties of various materials. One of the widely used methods for calculating the contact characteristics of the interaction of rough elastic and viscoelastic bodies is numerical simulation [1–3]. In this method, not only the shape of the interacting surfaces and the mutual influence of contact spots, but also effects such as adhesion and relative sliding in the contact area are taken into account [3]. However, the results obtained by numerical methods are difficult to use to evaluate the effect of the surface microgeometry on the characteristics of contact interaction. Therefore, in addition to numerical methods, analytical approaches based on various assumptions remain relevant. To take into account the effect of the surface microgeometry of contacting bodies on the contact characteristics at the macrolevel, Shtaerman [4] has proposed to extent the equation for contact pressures by including an additional function describing the compliance of the rough layer. In the

Greenwood–Williamson model [5], roughness is modeled by a set of spherical protrusions, whose elastic deformation is described by Hertz theory. For viscoelastic materials, a similar approach has been applied by Hui et al [6]. Argatov [7] has used averaging theory to solve the problem of contact between an elastic half-space and a punch with a fine-grained contacting surface. Abuzeid and Eberhard [8] have modeled a nominally flat area of contact of rough viscoelastic bodies using methods of fractal geometry. Persson et al. [9] have developed an approach based on probabilistic methods to study the contact of viscoelastic rough bodies at various scale levels.

In this paper, the indentation of a rigid cylinder with a rough flat base into a viscoelastic layer is investigated by studying the interaction of rough elastic bodies at two scale levels [10]. We consider both the problem of discrete contact (microlevel) and the problem of the interaction of bodies at the macrolevel taking into account the microrelief of the contacting surfaces.

1. FORMULATION OF THE PROBLEM

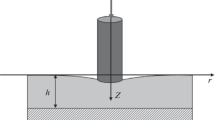
A rough rigid cylinder with a flat base of radius \(R\) is indented into a viscoelastic layer of small thickness \(h\) (with a small parameter \(\lambda = h/R\)) lying on a rigid base under a step load \(P(t) = P_0 H(t)\), where \(H(t)\) is a Heaviside function. The roughness is modeled by a system of identical asperities whose surface shape is described by the function \(f(r) = Cr^n/R_a^{n - 1}\) (\(n = 1,2,\dots\); \(R_a \) is a quantity characterizing the size of the protrusion; \(C\) is a dimensionless constant) and which are uniformly distributed with a given density on the contacting surface of the cylinder. The problem is considered using the following two scales (Fig. 1):

Fig. 1
figure 1

Schematic of the contact problem at the macroscale (a) and microscale (b) levels.

Full size image

(1) the microscale level corresponding to the size of an individual contact spot characterized by its radius \(a\), with \(a \ll h\) and \(a \ll R\);

(2) the macrolevel scale corresponding to the radius \(R\) of the nominally flat contact area (radius of the cylinder).

This approach is an extension of the method developed in [10] to solve problems of indentation of rough rigid bodies into an elastic layer or an elastic half-space for viscoelastic materials.

2. SOLUTION OF THE CONTACT PROBLEM AT THE MICROLEVEL

Below we solve the problem of indenting a cylinder with a rough base into a viscoelastic layer at the microlevel.

2.1. Formulation of the Problem of Discrete Contact and Its Reduction to the Corresponding Problem for an Elastic Half-Space

Taking into account the above assumptions about the size of an individual single contact spot (\(a \ll R\) and \(a \ll h)\) at the microlevel, we consider the periodic contact problem of the indentation of an infinite system of identical indenters simulating the microgeometry of the contacting surface of a cylinder into a viscoelastic half-space. It is assumed that the Poisson’s ratio of the material of the half-space does not depend on time, i.e., \(\nu = \mathrm{const}\). The periodic system is acted upon by a nominal (area-averaged) pressure \(\bar {p}(t)\), which is related to the load \(P_a (t)\) on each indenter as

$$ \bar {p}(t) = \bar {N}P_a (t),$$
(1)

where \(\bar {N}\) is the average number of protrusions per unit area. In the coordinate system attached to the center of an arbitrary contact spot \(\omega _i (t)\), the contact condition is written as

$$ w(x,y,t) = D(t) - f(x,y)H(t),\qquad (x,y) \in \omega _i (t).$$
(2)

Here \(w(x,y,t) = u_z (x,y,0,t)\) is the vertical displacement of the boundary of the viscoelastic half-space, \(D(t)\) is the indentation depth, and \(f(x,y)\) is the function describing the shape of the contacting surface of the indenter.

We now show that this problem reduces to a similar problem in an elastic formulation [11]. During indentation of a periodic system of pressure indenters into the half-space, the pressures \(p_i (x,y,t)\) at each contact spot \(\omega _i (t)\) are the same. Using the expression of vertical displacements of the boundary of the viscoelastic half-space under the action of a given pressure [12] and taking into account of the superposition principle, we can write the displacement function \(w(x,y,t)\) as

$$ w(x,y,t) = \frac{1 - \nu ^2}{\pi }\sum\limits_{i = 1}^\infty \int\limits_{0^ - }^t J(t - \tau )\, \frac{\partial }{\partial\tau } \Big(\;\mathop{\int\!\!\int}\limits_{\!\!\omega _i (\tau)} \frac{p_i (x',y',\tau )\,dx'\,dy'} {\sqrt {(x -x')^2 + (y - y')^2}}\Big)\,d\tau,$$
(3)

where \(J(t)\) is the creep function of the half-space material. The contacting surface of the indenters is described by a smooth function; therefore, the contact pressure is zero at the boundary of each contact area \(\omega _i (t)\). Further, if \(\omega _i (t)\) is a non-decreasing function of time and if the pressure outside the contact area is zero, in (3) we can change the order of the integration over time and the coordinate. As a result, we get

$$ w(x,y,t) = \frac{1 - \nu ^2}{\pi } \sum\limits_{i = 1}^\infty \;\mathop{\int\!\!\int}\limits_{\!\!\omega _i (t)} \frac{q_i (x,y,t)\,dx'\,dy'}{\sqrt {(x - x')^2 + (y -y')^2}},$$
(4)

where

$$ q_i (x,y,t) = \int\limits_{0^ - }^t J(t - \tau )\, \frac{\partial p_i (x,y,\tau )}{\partial \tau }\,d\tau.$$
(5)

The functions \(p_i (x,y,t)\) also satisfy the equilibrium condition

$$ P_a (t) = \mathop{\int\!\!\int}\limits_{\!\!\omega _i (t)} p_i (x,y,t)\,dx\,dy.$$
(6)

Taking into account (1), (5), and (6), we introduce the following quantity

$$ \bar {q}(t) = \bar {N} \mathop{\int\!\!\int}\limits_{\!\!\omega _i (t)} q_i (x,y,t)\,dx\,dy = \bar {N}\int\limits_{0^ - }^t J(t - \tau )\,\frac{\partial P_a (\tau)}{\partial \tau }\,d\tau = \int\limits_{0^ - }^t J(t - \tau )\, \frac{\partial \bar {p}(\tau)}{\partial \tau }\,d\tau.$$
(7)

If we consider \(t\) as a parameter, the mathematical formulation of the periodic contact problem for the viscoelastic half-space that includes Eqs. (4) and (6) and boundary condition (2), coincides with the formulation of the same problem in the elastic formulation when replacing the contact pressure by function (5).

2.2. Solution of the Discrete Contact Problem for an Elastic Half-Space

The periodic contact problem for spherical indenters and an elastic half-space is solved using the localization method [10] based on the solution obtained in [13] for the problem of indentation of a single indenter into a half-space in the presence of an additional load outside the contact area. The same method is used to solve the periodic contact problem for the indentation of a system of bodies with the surface given by the power-law function \(f(r) = Cr^n/R_a^{n- 1}\) into an elastic half-space.

In the study of the interaction of each indenter with the half-space using the localization method, the distribution of real pressures only under nearby indenters is taken into account, and the influence of the remaining indenters is replaced by the action of a nominal pressure distributed outside a circle of a certain radius. The accuracy of the method depends both on the number of indenters under which the real pressure distributions are taken into account (unknown in advance) and on the density of indenters. Below we investigate the simplest case where only one indenter is considered and the action of the remaining indenters is replaced by a nominal pressure \(\bar {p}\) uniformly distributed in a region \(r > A\); this imposes certain restrictions on the minimum distances between indenters that simulate surface asperities. Since the indenters are uniformly distributed over the surface of the half-space, the radius of the circular area \(A\) is determined only by the number \(\bar{N}\) of indenters per unit area:

$$ A^2 = 1/(\pi \bar {N}).$$
(8)

Thus, the boundary condition of the problem in cylindrical coordinates has the form

$$w(r) = D - f(r),\quad r \le a,$$
$$ p(r) = 0,\quad a \le r \le A,\qquad p(r) = \bar {p},\quad r > A,$$
(9)

where \(a\) is the radius of the contact area. The contact pressure \(p(r)\) satisfies the equilibrium condition

$$ P_a = 2\pi \int\limits_0^a rp(r)\,dr.$$
(10)

Taking into account the known dependence of the vertical displacements \(w(r)\) of the boundary of the elastic half-space on the pressures acting on it in the axisymmetric case [4] and boundary conditions (9), we obtain

$$ w(r) = \frac{4(1 - \nu ^2)}{\pi E} \Big(\int\limits_0^a p(\rho) K\Big(\frac{2\sqrt {r\rho }}{r + \rho }\Big) \frac{\rho\,d\rho }{r +\rho }+ + \bar {p}\int\limits_0^\infty K\Big(\frac{2\sqrt {r\rho}}{r + \rho }\Big) \,\frac{\rho\,d\rho }{r + \rho } -\bar{p}\int\limits_0^A K\Big(\frac{2\sqrt {r\rho } }{r + \rho }\Big)\, \frac{\rho\,d\rho }{r + \rho }\Big),$$
(11)

where \(K(x)\) is a complete elliptic integral of the first kind; the second integral in brackets defines the displacement of the boundary of the half-space loaded by nominal pressure over the entire surface; the value of the third integral in brackets is known:

$$\int\limits_0^A K\Big(\frac{2\sqrt {r\rho }}{r + \rho }\Big)\, \frac{\rho\,d\rho }{r + \rho } = AE\Big(\frac{r}{A}\Big),\qquad r \le A;$$

 \(E(x)\) is a complete elliptic integral of the second kind. The boundary conditions (9) and expression (11) for \(r \le a\) lead to the following integral equation for the contact pressure

$$ d - h(r) = \frac{4(1 - \nu ^2)}{\pi E}\int\limits_0^a p(\rho)K\Big(\frac{2\sqrt {r\rho }}{r + \rho }\Big)\, \frac{\rho\,d\rho }{r + \rho },\qquad r \le a,$$
(12)

where the functions \(d\) and \(h(r)\) are given by the expressions

$$ d = D - \frac{4(1 - \nu ^2)\bar {p}}{\pi E} \int\limits_0^\infty K\Big(\frac{2\sqrt {r\rho } }{r + \rho }\Big)\, \frac{\rho\,d\rho }{r + \rho };$$
(13)
$$ h(r) = f(r) - \frac{4(1 - \nu ^2)A}{\pi E}\,E\Big(\frac{r}{A}\Big)\bar {p}.$$
(14)

The function \(d\) depends on the nominal pressure and defines the additional displacement [10], i.e., the difference in displacement between the boundaries of the body with a rough surface characterized by the shape of an individual protrusion and the density of the protrusions and boundaries of the body with a smooth flat surface. The function \(h(r)\) is the value of the gap between the indenter and the curved surface of the elastic half-space that results from the action of the nominal pressure outside the circle of radius \(A\).

The solution of the integral equation (12) in general form is given in [4, 10]. Substituting the function \(h(r)\) (14) into this solution, we obtain the expressions for the contact pressure and the indentation depth \(d\)

$$ p(r) = \frac{E}{\pi (1 - \nu ^2)} \Big(\frac{Cp_{k(m)} (r)}{R_a^{n - 1} } +\frac{2(1 - \nu ^2)\bar {p}}{E}\,\arctan\Big(\frac{\sqrt {a^2 - r^2} }{\sqrt {A^2 - a^2}}\Big)\Big),\quad r \le a;$$
(15)
$$ d = \frac{2^{n - 2}n\Gamma ^2(n/2)}{\Gamma (n)}\, \frac{Ca^n}{R_a^{n- 1} } - 2(1 - \nu ^2)\bar {p}\sqrt {A^2 - a^2}\,,$$
(16)

[3] where

$$ p_k (r) = \Big(\frac{(2k + 1)!!}{(2k)!!}\Big)^2 r^{2k}\Big(\mathrm{ arch}\Big(\frac{a}{r}\Big) + \sqrt{1 - \Big(\frac{r}{a}\Big)^2}\; \sum\limits_{i = 1}^k \frac{(2i- 2)!!}{(2i - 1)!!} \Big(\frac{a}{r}\Big)^{2k}\Big)$$
(17)

for odd powers, i.e., for \(n = 2k + 1\) (\(k\) is an integer),

[3]

$$ p_m (r) = \Big(\frac{(2m)!!}{(2m - 1)!!}\Big)^2a^{2m - 1} \sqrt {1 - \Big(\frac{r}{a}\Big)^2}\; \sum\limits_{i = 1}^m \frac{(2i - 3)!!}{(2i - 2)!!} \Big(\frac{r}{a}\Big)^{2(m - i)}$$
(18)

for even powers, i.e., for \(n = 2m\) (\(m\) is a natural number); \(\Gamma (x)\) -is the gamma function. Substituting (15) into the equilibrium condition (10) and using (1), (8), we have the following relation between the radius of the contact area and the nominal pressure:

$$ \frac{(n + 1)\Gamma (n)R_a^{n - 1} } {2^{n -2}n^2\Gamma ^2(n/2)C}\,\frac{(1 - \nu ^2)\bar {p}}{E} = \frac{a^{n + 1}}{A^2\arccos\,(a/A) + a\sqrt {A^2 - a^2}}.$$
(19)

2.3. Solution of the Discrete Contact Problem for a Viscoelastic Half-Space

In the case of a viscoelastic half-space with instantaneous elastic modulus \(E_0 \), the radius of the contact spot, the additional displacement values, and the contact pressure distribution at the initial time \(t = 0\) are determined from expressions (15)–(19). Substituting the long-term modulus \(E_\infty\) (if the viscoelastic material model has a finite long-term elastic modulus) into (15)–(19), we obtain the values of the contact characteristics at long times. The right-hand side of expression (19) is a monotonically increasing function of the radius of the contact area. Therefore, in the case of a constant nominal pressure, since \(E_0 > E_\infty\), the instantaneous radius of the contact spot will be smaller than the long-term radius: \(a(0)< a(\infty)\). This implies that under the action of the constant nominal pressure, the radius \(a(t)\) of the contact area of a unit indenter with a viscoelastic half-space is an increasing function of time. Therefore, the viscoelastic problem can be solved using the correspondence principle [14].

Thus, expressions (15)–(19) are a solution of the viscoelastic problem if the function \(p(r)/E\) is replaced by the function \(q(r,t)\) given by expression (5) and if the function \(\bar {p}/E\) is replaced by the function \(\bar {q}(t)\) given by expression (7). As a result, we get

$$\qquad\qquad\int\limits_{0^ - }^t J(t - \tau )\, \frac{\partial p(\rho ,\tau )}{\partial \tau }\,d\tau = \frac{1}{\pi (1 - \nu^2)} \Big(\frac{Cp_{k(m)} (r,t)}{R_a^{n - 1}}+{}$$
$$ {}+ 2(1 - \nu ^2)\Big(\int\limits_{0^ - }^t J(t - \tau )\,\frac{d\bar {p}(\tau)}{d\tau}\,d\tau\Big) \arctan\Big(\frac{\sqrt {a^2(t) - r^2}}{\sqrt{A^2 - a^2(t)}}\Big)\Big), \quad r \le a(t);\qquad\qquad$$
(20)
$$ d(t) = \frac{2^{n - 2}n\Gamma ^2(n/2)}{\Gamma (n)}\, \frac{Ca^n(t)}{R_a^{n - 1} } -2(1 - \nu ^2)\Big(\int\limits_{0^ - }^t J(t - \tau)\,\frac{d\bar {p}(\tau)}{d\tau}\,d\tau\Big) \sqrt{A^2 - a^2(t)}\,;$$
(21)
$$ \qquad\frac{a^{n + 1}(t)}{A^2\arccos\,(a(t)/A) + a(t)\sqrt {A^2 -a^2(t)}} =\frac{(n + 1)\Gamma (n)R_a^{n - 1} (1 - \nu ^2)}{2^{n - 2}n^2\Gamma ^2(n/2)C} \Big(\int\limits_{0^ - }^t J(t - \tau )\, \frac{d\bar {p}(\tau)}{d\tau }\,d\tau\Big).$$
(22)

Using the well-known relation between the creep function \(J(t)\) and the relaxation function \(E(t)\) [14], from (20) we obtain the following expression for the contact pressure distribution (\(r \le a(\tau)\)):

$$\qquad\qquad p(r,t) = \frac{1}{\pi (1 - \nu ^2)}\int\limits_{0^ - }^t E(t - \tau )\,\frac{\partial p_{k(m)} (r,\tau )}{\partial \tau }\,d\tau+{}$$
$$ {}+ \frac{2}{\pi }\int\limits_{0^ - }^t E(t - \tau )\,\frac{\partial }{\partial \tau } \Big(\Big(\int\limits_{0^ -}^\tau J(\tau - s)\,\frac{d\bar {p}(s)}{ds}\,ds\Big) \arctan\Big(\frac{\sqrt {a^2(\tau) - r^2} }{\sqrt{A^2 - a^2(\tau)}}\Big)\Big)\,d\tau.\qquad\qquad$$
(23)

2.4. Model of a Standard Viscoelastic Solid

To study the time dependence of the characteristics of the contact interactions (21)–(23), we consider the model of a standard viscoelastic solid for which the relaxation and creep functions have the form [14]

$$ E(t) = E\Big(1 + \frac{T_\varepsilon - T_\sigma }{T_\sigma} \mathrm{e}^{ -t/T_\sigma}\Big),\qquad J(t) = \frac{1}{E}\Big(1 - \Big(1 - \frac{T_\sigma}{T_\varepsilon }\Big) \mathrm{e}^{ -t/T_\varepsilon}\Big),$$
(24)

where \(E\) is the long-term elastic modulus; \(T_\sigma \) and \(T_\varepsilon \) are the relaxation and creep times. Substituting (24) into (21) and (22) and taking into account that \(\bar {p}(t) = p_0 H(t)\), where \(p_0 = P_0/(\pi R^2)\), we obtain

$$ d(t) = \frac{2^{n - 2}n\Gamma ^2(n/2)}{\Gamma (n)}\, \frac{Ca^n(t)}{R_a^{n - 1} } - \frac{2(1 - \nu ^2)p_0 }{E} \Big(1 - \Big(1 -\frac{T_\sigma }{T_\varepsilon }\Big) \mathrm{e}^{ -t/T_\varepsilon}\Big)\sqrt {A^2 - a^2(t)}\,;$$
(25)
$$ \frac{a^{n + 1}(t)}{A^2\arccos\,(a(t)/A) + a(t)\sqrt {A^2 - a^2(t)}}=\frac{(n + 1)\Gamma (n)R_a^{n - 1} (1 - \nu ^2)p_0 }{2^{n - 2}n^2\Gamma ^2(n/2)CE} \Big(1 - \Big(1 - \frac{T_\sigma }{T_\varepsilon }\Big) \mathrm{e}^{-t/T_\varepsilon}\Big).$$
(26)

Since the function \(a(t)\) is strictly monotonic, there exists its inverse function \(t(a)\). For the inverse function \(t(a)\), from expressions (26) we obtain

$$ t(a) = - T_\varepsilon \ln\Big( \frac{T_\varepsilon}{T_\varepsilon - T_\sigma } \Big(1 - \frac{2^{n - 2}n^2\Gamma ^2(n/2)CEa^{n + 1}R_a^{1 - n} (n + 1)^{-1}} {\Gamma (n)(1 - \nu ^2)p_0 (\arccos\,(a/A) + a\sqrt {A^2 - a^2}\,/A^2)}\Big)\Big).$$
(27)

Then, integrating (23) by parts and passing to the new variable \(a\), for the contact pressure, we have the expression (\(r \le s\), \(s\equiv a(\tau)\))

$$\qquad\qquad p(r,a) = \frac{ET_\varepsilon C}{\pi (1 - \nu ^2)T_\sigma R_a^{n - 1} } \Big(p_{k(m)} (r,a) + 2\varphi _n (a) -{}$$
$$ {} - \frac{T_\varepsilon - T_\sigma }{T_\sigma T_\varepsilon } \mathrm{e}^{ -t(a)/T_\sigma}\int\limits_{a_0 }^a (p_{k(m)} (r,s) + 2\varphi _n (s))\mathrm{e}^{t(s)/T_\sigma}\, \frac{dt(s)}{ds}\,ds\Big),\qquad\qquad$$
(28)

where \(a_0 \equiv a(0)\) and the function \(\varphi _n \) is given by

$$ \varphi _n (x) = \frac{2^{n - 2}n^2\Gamma ^2(n/2)}{(n + 1)\Gamma(n)}\, \frac{x^{n +1}\arctan\,(\sqrt {x^2 - r^2}\,\big/\sqrt {A^2 - x^2}\;)} {A^2\arccos\,(x/A) + x\sqrt {1 - (x/A)^2}}.$$
(29)

Expressions (27) and (28) make it possible to determine the contact pressure distribution at each time, i.e., the function \(p(r,a(t))\). The time dependence of the radius of the contact region \(a(t)\) and the additional displacement function \(d(t)\) are given by expressions (25) and (26).

2.5. Results of Numerical Calculations

From the solution constructed in Subsections 2.1–2.3, it follows that the contact characteristics at the microlevel depend on the shape of an individual protrusion (parameters \(C\), \(R_a\), and \(n\)), the density of the protrusions (parameter \(A\)), and the mechanical characteristics of the viscoelastic layer (parameters \(E\), \(T_\sigma \), and \(T_\varepsilon\)). Consider the case where the indenters are located at the nodes of a hexagonal mesh with a pitch size \(l\). Then \(A = \sqrt[4]{3}\,l/\sqrt {2\pi }\).

We introduce the following dimensionless quantities:

$$\tilde {p} = \frac{(1 - \nu ^2)p}{E},\quad \tilde {r} = \frac{r}{R_a },\quad \tilde {a} = \frac{a}{R_a },\quad \tilde {d} = \frac{d}{R_a },\quad \tilde {l} = \frac{l}{R_a },\quad \tilde {t} = \frac{t}{T_\varepsilon },\quad T = \frac{T_\varepsilon }{T_\sigma }.$$

The parameter \(T\) characterizes the relaxation properties of the viscoelastic half-space; for the elastic half-space, \(T = 1\). The constant \(C\) and the quantity \(R_a \) characterize the shape and size of an individual protrusion. Thus, for \(n = 1\) (conical protrusion), \(C = \cot\theta \), where \(2\theta \) is the opening angle; for \(n = 2\) ( spherical protrusion), \(C/R_a = R_s/2\), where \(R_s \) is the radius of curvature of the contacting surface of the protrusion. The parameter \(\tilde {l}\) defines the dimensionless distance between the indenters, i.e., the density of indenters on the boundary of the half-space.

Fig. 2
figure 2

Time dependence of the additional displacement \(\tilde {d}(\tilde{t})\) for \(\tilde {p}_0 = 0.005\) and \(C = 1\): (a) \(n =2\) (\(\tilde {l} = 0.25\) (1), \(\tilde {l} =0.5\) (2), \(\tilde {l} = 1\) (3)), (b) \(\tilde {l} = 0.25\)(\(n =1\) (1), \(n = 2\) (2), \(n =3\) (3)); solid curves correspond to \(T = 10\), and dashed curves to \(T = 1\).

Full size image

We analyze the dimensionless function \(\tilde {d}(\tilde t)\) of the additional displacement of the half-space boundary in the case of discrete interaction for different shapes of protrusions (indenters) characterized by the parameter \(n\) and different dimensionless distances \(\tilde {l}\) between them. It follows from the calculation results that the additional displacement is a monotonically increasing function of time, which tends to the limiting value corresponding to the additional displacement for the elastic half-space with long-term elastic modulus \(E\)(expression (25) at \(T = 1\)) (Fig. 2). Moreover, the denser the indenters, the smaller the additional displacement at the same nominal pressure (see Fig. 2a). For the parameter values considered, a twofold increase in the distance between the protrusions leads to a factor of more than 2.5 increase in the additional displacement. The additional displacement is also larger for indenters whose surface shape is described by a function with a smaller exponent (see Fig. 2b). The protrusion shape has a significant effect on the additional displacement function. For example, for a system of indenters with \(n = 2\), the value of the additional displacement for the parameter values considered is six times less than that for the system with \(n = 1\).

Fig. 3
figure 3

Dependence of the additional displacement on nominal pressure \(\tilde {d}(\tilde {p}_0)\) at the time \(\tilde {t} = 1\) for \(C = 1\), \(n= 2\), \(\tilde {l} = 0.25\) and \(T = 1\) (curve1)), \(T = 2\) (2), \(T = 5\) (3), and \(T = 100\) (4).

Full size image

For the case of spherical asperities and a fixed distance between them, we constructed dependences \(\tilde {d}(\tilde{p}_0 )\) for different values of the parameter \(T\) (Fig. 3), which made it possible to investigate the influence of the viscoelastic properties of the half-space on the additional displacement function at a fixed time. It follows from the results that with an increase in the nominal pressure, the additional displacement increases and the difference in additional displacements between materials with different viscosities increases. Analysis of the dependence \(\tilde {d}(\tilde t)\) for different values of the parameter \(T\) shows that the larger the value of the parameter \(T\) for a fixed long-term elastic modulus, the lower the instantaneous value of the additional displacement and the longer the time to reach its value for the long-term elastic modulus.

Fig. 4
figure 4

Contact pressure distribution on an individual contact spot \(\tilde{p}(\tilde {r},1)\) for \(C = 1\), \(\tilde {l} = 0.25\), \(T = 10\): (a) \(n = 1\) (\(\tilde {p}_0 =0.1\) (1), \(\tilde {p}_0 = 0.2\) (2), \(\tilde {p}_0 = 0.3\) (3)), (b) \(n = 2\) (\(\tilde {p}_0 = 0.01\) (1), \(\tilde {p}_0 =0.02\) (2), \(\tilde {p}_0 =0.03\) (3)); solid curves correspond to a system of indenters, and dashed curves to a single indenter.

Full size image

It is of interest to study the contact pressure distribution at each spot, which varies with time and depends on the density of the indenters, their shape, the nominal pressure, and the viscoelastic properties of the half-space. From the results of numerical calculations, it follows that the contact spot pressure is redistributed over time: at the initial time, it corresponds to the solution of the problem for an elastic half-space (taking into account the density and the mutual influence of contact spots), and at large times, to the solution of the problem of discrete contact for an elastic half-space with long-term elastic modulus. In the central part of the contact area, the pressure decreases significantly over time for any indenter shape. Due to the nonuniform pressure relaxation and due to the non-simultaneous contact of the boundary of the half-space, additional maxima appear at the edge of the contact area with time. At low nominal pressure, the ratio of the radius of the contact spot to the distance between the spots is small; therefore, the pressure distribution is practically the same as in the case of indentation of a single indenter into a viscoelastic half-space. Figure 4 shows the contact pressure distribution under an individual protrusion of conical and spherical shapes at a fixed time for different nominal pressures. For comparison, the figure shows the distributions in the case of indentation of a single indenter into a viscoelastic half-space. It follows from the results that the higher the nominal pressure, i.e., the density of real contact spots, the higher the mutual influence of the protrusions, resulting in a decrease in the radius of an individual contact spot and an increase in the pressure in the central part of the contact area.

3. SOLUTION OF THE CONTACT PROBLEM AT THE MACROLEVEL

Below the problem of indentation of a cylinder with a rough base into a viscoelastic layer is solved at the macrolevel.

3.1. Formulation of the Problem

As shown in [10], at the macrolevel, the solution of the problem of determining nominal pressures during the indentation of a punch with a flat end surface having a periodic system of microroughnesses into a deformable base reduces to solving the integral equation

$$ D - d[p(x,y)] = \mathop{\int\!\!\int}\limits_{\!\!\Omega} K(x,y,x',y')p(x',y')\,dx'\,dy',\qquad (x,y) \in \Omega .$$
(30)

Here \(d[p]\) is the additional displacement function determined by solving the periodic problem at the microlevel; \(\Omega \) is the nominal contact area; \(p(x,y)\) is the distribution of the nominal pressure in the region \(\Omega \); \(D\) is the indentation depth of a cylindrical punch into the base; the kernel \(K(x,y,x',y')\) of the integral operator depends on the model describing the stress-strain state of the base. In the case of an elastic layer, the kernel \(K(x,y,x',y')\) has the form [15]

$$K(x,y,x',y') = \frac{1 - \nu ^2}{\pi hE}\,k\Big(\frac{R}{h}\Big),$$
$$R = \sqrt {(x - x')^2 + (y - y')^2},\qquad k(s) = \int\limits_0^\infty L(u)J_0(us)\,du.$$

Here \(J_0 (x)\) is a zero-order Bessel function; the function \(L(u)\) depends on the method of attaching the layer to the non-deformable base: \(L(u)=(2\kappa \sinh\,(2u) - 4u)/(2\kappa \sinh\,(2u) +4u^2 + 1 + \kappa ^2)\), \(\kappa = 3 - 4\nu\) in the absence of friction, \(L(u)=(\cosh\,(2u) - 1)/(\sinh\,(2u) + 2u)\) in the case of complete adhesion. The second term on the left-hand side of expression (30) defines the additional displacement of the boundary of the base due to the microrelief, and the right-hand side defines the displacement of the boundary of the base due to the action of the nominal pressure in the domain \(\Omega \). The additional displacement function \(d\) for a viscoelastic base is found in section 2, and the displacements of the boundary of the viscoelastic layer are determined using the correspondence principle [14] (since the contact area is constant). Thus, in the case of a viscoelastic layer, expression (30) takes the form (\((x,y) \in \Omega\))

$$ D(t) = d[p(x,y,t)] + \frac{1 -\nu ^2}{\pi h} \mathop{\int\!\!\int}\limits_{\!\!\Omega} k\Big(\frac{R}{h}\Big) \Big(\int\limits_{0^ - }^t J(t - \tau )\,\frac{dp(x',y',\tau)}{d\tau }\, d\tau\Big)\,dx'\,dy'.$$
(31)

In this case, the equilibrium condition must be satisfied:

$$ P(t) = \mathop{\int\!\!\int}\limits_{\!\!\Omega} p(x,y,t)\,dx\,dy.$$
(32)

3.2. Solution of the Problem at the Macrolevel Taking into Account the Characteristics of the Discrete Contact at the Microlevel

Since a thin layer is considered, for the kernel \(k(s)\) we can use the asymptotic approximation [16]

$$k(s) \sim 2\pi B\delta (s),$$

where \(\delta (s)\) is a two-dimensional delta function; the constant \(B\) depends on the type of attachment of the layer to the rigid base. If there is no friction between the layer and the rigid base, then \(B = 1/2\); if there is adhesion between the layer and the base, then \(B = 4(\kappa - 1)/(\kappa + 1)^2\), \(\kappa = 3 -4\nu \) [15]. Then for the vertical displacements of the boundary the layer and the pressures causing them, we obtain the relation

$$ w(x,y,t) \sim 2hB(1 - \nu ^2) \Big(\int\limits_{0^ - }^t J(t - \tau )\,\frac{dp(x,y,\tau)}{d\tau}\,d\tau\Big).$$
(33)

[3] As noted in [15], relation (33) is valid only in the inner part of the contact area, and not in over the entire area. However, the smaller the thickness of the layer, the larger the area in which this relation is valid. The value of the layer thickness for which this approximation is applicable is given in [16].

Transforming to cylindrical coordinates and using (31) and (33), we obtain the equation

$$D(t) = d[p(r,t)] + 2hB(1 -\nu ^2) \Big(\int\limits_{0^ - }^t J(t - \tau )\,\frac{dp(x,y,\tau)}{d\tau}\, d\tau\Big),\qquad r < R.$$

Substituting into this equation the function \(d(t)\) (21) determined from the solution of the periodic contact problem at the microlevel, we obtain the dependence of the indentation depth \(D(t)\) on the nominal pressure \(p(r,t)\) under the surface of the cylinder (\(r < R\))

$$D(t) = \frac{n\Gamma ^2(n/2)}{2^{2 -n}\Gamma (n)}\, \frac{Ca^n(t)}{R_a^{n - 1} } +2\big(hB - \sqrt {A^2 - a^2(t)}\;\big)(1 - \nu ^2) \Big(\int\limits_{0^ - }^t J(t - \tau )\, \frac{dp(r,\tau )}{d\tau}\,d\tau\Big),$$

where the dependence of the radius of an individual contact spot on the nominal pressure \(a(t)\) is given by expression (22). The above relations imply that the nominal (averaged) contact pressure is evenly distributed under the surface of the cylinder. This is due to the use of the simplified dependence (33). In view of the equilibrium condition (32), \(p(t) = P(t)/(\pi R^2)\). Finally we obtain the following system of equations for determining the time variation in the indentation depth \(D(t)\) and the radius \(a(t)\) of a single contact spot at given load \(P_0 \) applied to the cylinder:

$$D(t) = \frac{2^{n - 2}n\Gamma ^2(n/2)}{\Gamma (n)}\, \frac{Ca^n(t)}{R_a^{n - 1} } +\frac{2(1 - \nu ^2)J(t)P_0 }{\pi R^2}\, \big(hB- \sqrt {A^2 - a^2(t)}\;\big),$$
$$ \frac{a^{n + 1}(t)}{A^2\arccos\,(a(t)/A) + a(t)\sqrt {A^2 - a^2(t)} } = \frac{(n + 1)\Gamma (n)R_a^{n - 1} (1 - \nu ^2)}{2^{n - 2}n^2\Gamma ^2(n/2)C\pi R^2}\, J(t)P_0 .$$
(34)

3.3. Constitutive Relations for the Model of a Viscoelastic Solid

For the model of a standard viscoelastic solid considered in Section 2, in view of (24), expressions (34) take the form

$$D(t) = \frac{n\Gamma ^2(n/2)}{2^{2 -n}\Gamma (n)}\, \frac{Ca^n(t)}{R_a^{n - 1} } + \frac{2(1 - \nu ^2)P_0 }{\pi R^2E} \Big(1 - \Big(1 -\frac{T_\sigma }{T_\varepsilon }\Big) \mathrm{e}^{-t/T_\varepsilon}\Big) \big(hB - \sqrt {A^2 - a^2(t)}\;\big),$$
$$ \frac{a^{n + 1}(t)}{A^2\arccos\,(a(t)/A) + a(t)\sqrt {A^2 - a^2(t)}}= \frac{(n + 1)\Gamma (n)R_a^{n - 1} (1 - \nu ^2)P_0 }{2^{n - 2}n^2\Gamma ^2(n/2)C\pi R^2E} \Big(1 - \Big(1 - \frac{T_\sigma }{T_\varepsilon }\Big) \mathrm{e}^{ -t/T_\varepsilon}\Big).$$
(35)

The size of an individual contact spot can be used to determine the real contact area, which is the sum of the areas of all real contact spots. We assume that the asperities forming the microrelief of the base of the cylinder are located at the nodes of a hexagonal mesh with a pitch size \(l\). Then the real contact area under a cylinder of radius \(R\) is given by

$$ A_r (t) = 2\pi \int\limits_0^R r\beta (t)\,dr= \pi R^2\beta (t),$$
(36)

where the function \(\beta (t) = 2\pi a^2(t)/(\sqrt 3 l^2)\) characterizes the ratio of the real contact area to the nominal one.

Relations (35) and (36) show that, like the characteristics at the microlevel, the contact characteristics at the macrolevel depend on the microgeometry of the cylinder base surface (parameters \(C\), \(R_a\), \(n\), \(l\)) and on the mechanical characteristics of the viscoelastic layer (\(E\), \(T_\sigma \), \(T_\varepsilon\)). We introduce the following dimensionless quantities:

$$\tilde {P}_0 = \frac{(1 - \nu ^2)P_0 }{ER^2},\quad \tilde {a} = \frac{a}{R},\quad \tilde {D} = \frac{D}{R},\quad \tilde {l} = \frac{l}{R},\quad \tilde {R}_a = \frac{R_a }{R},\quad \tilde {t} = \frac{t}{T_\varepsilon },\quad T = \frac{T_\varepsilon }{T_\sigma }.$$

Then the dimensionless indentation depth \(\tilde {D}(\tilde {t})\) and the real contact area \(\beta( \tilde {t})\) at arbitrary time \(\tilde {t}\) depend on the following dimensionless parameters:

— the parameters \(C\), \(\tilde {R}_a \), and \(n\), which characterize the shape of the asperities forming the microrelief of the cylinder surface;

— the relative distance between asperities \(\tilde {l}\), which characterizes their density on the punch surface;

— the characteristics of the viscoelastic layer \(B\), \(\lambda \), and \(T\);

— the load \(\tilde {P}_0\) applied to the cylinder.

The parameters characterizing the thickness of the layer (parameter \(\lambda\)) and the manner of its attachment (the parameter \(B\)) are included (linearly) only in the expression for the indentation depth. Therefore, their influence on the time dependences of the macrocharacteristics on is obvious. We assume that \(B = 0.5\) and \(\lambda = 0.1\), and investigate the influence of the microgeometry parameter \(\tilde {l}\) and the relaxation characteristics of the layer \(T\) on the indentation depth and the real contact area.

Fig. 5
figure 5

Time dependences of the real contact area (a) and the indentation depth (b) for \(\tilde {P}_0 = 0.005\), \(n = 2\), \(C = 1\), \(\tilde {R}_a =0.01\), \(T = 10\): (1–3) rough cylinder (\(\tilde {l} = 0.0025\) (1), \(\tilde {l} = 0.005\) (2), \(\tilde {l} = 0.01\) (3)), (4) smooth cylinder; solid curves correspond to the viscoelastic layer, and dashed curves to the elastic layer.

Full size image
Fig. 6
figure 6

Real contact area (a) and the indentation depth (b) versus the applied load \(\tilde {P}_0 \) at the time \(\tilde {t} = 1\) for \(C = 1\), \(n = 2\), \(\tilde {R}_a = 0.01\), \(\tilde {l} = 0.01\): \(T = 1\) (1), \(T = 2\) (2), \(T = 5\) (3), \(T = 100\) (4); solid curves correspond to a rough cylinder, and dashed curves to a smooth cylinder.

Full size image

3.4. Analysis of the Influence of Microgeometry Parameters on the Indentation Depth of the Punch and the Real Contact Area

The microrelief of the cylinder base surface is characterized by the shape of asperities and their density. To analyze the effect of the density of asperities, we plotted the time dependences of the indentation depth and the real contact area characterized by value \(\beta\) (36) for different pitch sizes \(\tilde {l}\) of the hexagonal mesh (Fig. 5). It follows from the calculation results that an increase in the density of asperities (as an increase in the parameter \(R_a \)) leads to an increase in the real contact area and a decrease in the indentation depth; furthermore, the results of solving the problem approach the results of solving the problem of indentation of a cylinder with a smooth base. Figure 5 also shows the values of the real contact area and the indentation depth characteristic of an elastic layer with a long-term elastic modulus. It is seen that for a fixed value of the parameter \(T\) characterizing the viscosity of the layer, the investigated quantities reach the long-term value within the same time.

3.5. Analysis of the Influence of the Viscoelastic Properties of the Layer and the Applied Loads on the Indentation Depth of the Punch and the Real Contact Area

To analyze the influence of the viscoelastic properties of the layer on the time variation of the investigated contact characteristics, we calculated the time dependence of the real contact area and the indentation depth for different values of the parameter \(T\), which is equal to the ratio of the creep and relaxation times of the layer. From the calculation results, it follows that the higher the viscosity of the material (parameter \(T\)) for the same long-term elastic modulus, the smaller the real contact area and the indentation depth of punch at the initial time. Comparison of the results with the results obtained in the case of indentation of a smooth cylinder allows us to conclude that the presence of microrelief leads to an increase in the indentation depth; furthermore, the difference between the results obtained with and without microrelief increases with time and reaches a constant value.

The influence of the value of the load applied to the cylinder on the characteristics under study was also investigated. For this, we obtained the dependences of the real contact area (Fig. 6a) and indentation depth (Fig. 6b) on the load at a fixed time for materials with different viscosities characterized by the parameter \(T\). It follows from the results that both the contact area and the indentation depth increase with increasing applied load. Comparison of the dependences of the indentation depth on load for the rough and smooth cylinders shows that in the case of the cylinder with a surface microrelief at a small load, this dependence is not linear. Furthermore, the lower the contact density, the greater the deviation of the dependence \(D(P) \) from linearity. Increasing the viscosity of the layer material leads to a decrease in both the indentation depth and the real contact area for fixed values of the load applied to the punch and time.

CONCLUSIONS

A model for the indentation of a rigid cylinder with a rough end surface into a viscoelastic layer under the action of a constant force was developed. The case of a thin layer and roughness modeled by a periodic system of identical indenters with the contacting surface described by a power-law function was considered.

The formulated contact problem was solved at two scale levels: at the microlevel (size of a single contact spot) and at the macrolevel (radius of the base of the cylinder). At each scale level, the influence of the microrelief parameters and the mechanical properties of the layer on the characteristics of contact interaction was investigated.

[3] The results of the obtained analytical solution of the problem show that the shape of the protrusions and their density on the surface of the indentation punch have a significant effect on the additional displacement function due to the roughness of the punch base, which, in turn, leads to a change in the rigidity contact at the macrolevel. In particular, with decreasing density of of protrusions on the rough surface and with decreasing exponent of the function describing the roughness shape, the dependence of the indentation depth of the punch at the macrolevel on the load applied to it becomes nonlinear. In addition, the time dependence of the real contact area for different shapes of asperities and the density of their location on the punch surface was analyzed.

The effect of the relaxation properties of the layer material on the contact characteristics (indentation depth of the punch and real contact area) and their time variation were investigated. It was shown that an increase in the viscosity of the layer material (with a fixed long-term modulus elasticity) leads to a decrease in the indentation depth of the punch and the real contact area for a fixed time.

The developed model and the results of the study can be used to evaluate the rigidity of contact of bodies with rough surfaces and to control the microgeometry parameters of conjugated surfaces in order to achieve the required contact characteristics (contact rigidity, real contact area) and estimate the time for these characteristics to reach stationary values upon contact of bodies made of viscoelastic materials.

This work was supported by the Russian Science Foundation (Project No. 18-19-00574-P).