INVESTIGATION OF THE LONGEVITY OF MATERIALS ON THE BASIS OF THE KINETIC CONCEPT OF FRACTURE

Abstract

Experimental data on the failure and deformation of various materials are considered from the viewpoint of the kinetic concept of fracture as thermodynamic processes occurring over time. Mathematical modeling of the general and local plastic flows in materials is based on rheological models of a solid with due allowance for damage accumulation. The prediction of the longevity of materials under constant or variable temperature and force conditions is performed by time steps, including situations with changes in the material structure. A single fracture criterion is used, which implies that fracture occurs after reaching a threshold damage concentration (concentration criterion) in a certain volume of the solid body.

INTRODUCTION

The analysis of strength properties of materials and prediction of their longevity are based on the reaction rate theory, which was developed in 1935. The first study of the flow of solids with the use of the reaction rate theory was performed in 1941 [1]. Since the 1950s, the longevity of materials has been investigated at the Ioffe Institute of the Russian Academy of Sciences, and a kinetic concept of fracture was developed [2–5].

Based on this concept, the analysis of strength and deformation characteristics of any material should be started from the analysis of results of simple experiments on fracture at constant stress and temperature to identify the basic features of the process. Additional tests performed under monotonic loading provide additional data, which may ensure a more accurate description of the material behavior [6]. In this case, the main research method is the thermoactivation analysis.

Fig. 1

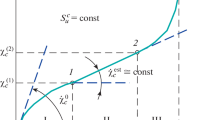
Specific FAE for Duralumin specimens versus stress for different types of loading and different temperatures: (a) constant loading at $T=398$ (1), 423 (2), 448 (3), and 473 K (4); (b) increasing loading at $T=77$ (1), 123 (2), 223 (3), 293 (4), 373 (5), 423 (6), 473 (7), 523 (8), and 573 K (9); (I) approximation of experimental data at constant loading; (II) approximation of experimental data at different strain rates and temperatures; (III) experimental data obtained at $T=293$ K and different types of loading.

We consider Duralumin under various loading conditions. Figure 1 shows the specific fracture activation energy (FAE) of Duralumin specimens as a function of stress for different types of loading and different temperatures. If the load is slowly increased for a certain unchanged temperature, then the experimental values of the specific FAE are approximated by the straight line I corresponding to constant loading. In the case of fast loading or a decrease in temperature, the experimental points are approximated by the straight line II. These points correspond to higher internal stresses in local volumes of the material where the fracture occurs [2–5]. The difference in the tangents of the slopes of the straight lines I and II is caused by the difference in the relaxation processes [3]. The experimental points located along curve III correspond to the transition from the straight line I to the straight line II. Such a transition corresponds to different relationships of the fracture rate and the rate of relaxation of internal stresses for different loading rates and an identical temperature. Similar dependences were obtained for steel [7], but for different rates of the relaxation processes [6]. It should be noted that specific features of low-temperature fracture [4, 6, 7] should be taken into account in constructing these dependences.

If the material structure does not experience significant changes, then the force dependence of the specific FAE on stress is a straight line [2–7]:

$$U(\sigma ) = U_0 - \gamma \sigma \in RT\ln\,(\tau \nu _0 ).$$

Here $\tau$ is the time before fracture (longevity) of each specimen at the absolute temperature $T$ and stress $\sigma$, $R$ is the universal gas constant, and $\nu_0=10^{13}$ s$^{-1}$ is the characteristic Debye frequency [4]. The coefficient $\gamma$ depending on the material structure, which is called the activation volume, characterizes the internal stress values at the so-called fracture centers [2–5]. In the case of loads growing with time, the equivalent time to fracture corresponding to the maximum stresses of specimen fracture is calculated via the integral of the fracture rate with respect to time. The fracture rate is understood as a quantity inverse to longevity [6]. The equivalent time to fracture $\tau_{\mathrm eq}$ is calculated in accordance with the Bailey criterion [8]

$$\tau _{\mathrm eq} \nu _0 \exp \Big(- \frac{U_0 - \gamma \sigma _ * }{RT}\Big) = \int\limits_0^{t_ * } \dot {\omega }\,dt = 1,$$

where $t_ *$ is the time of loading along this or that trajectory up to the stress $\sigma _ *$ at which specimen fracture occurs.

The damage accumulation rate is calculated by the formula

$$\dot {\omega } = \nu _0 \exp\Big( - \frac{U_0 - \gamma (t,\sigma ,T)\sigma (t)}{RT(t)}\Big).$$

(1)

When the damage size or the number of damages in some local volume of the material reaches such values that the distance between the damaged regions becomes comparable with the damage size, coalescence of damages occurs, followed by the formation of significant discontinuity in the material. This process was photographed by an atomic force microscope in the case of crack propagation in glass [9].

Loading with continuously increasing loads provides an idea about the strength properties of the material and allows one to determine the ranges of temperature and loading whose detailed analysis requires additional experiments. In the case of loading the material specimen with a specified loading rate, the time to fracture is assigned and the corresponding stresses are determined. These stresses correspond to the end of the failure process. As the fracture rate (1) is an exponential function of stress, fracture mainly proceeds within a moderate time interval at stresses close to $\sigma _ *$, and the resultant value of $\gamma$ corresponds to this time instant within a small error [10].

The processes of material fracture and deformation are closely related to each other. The product of the rate of steady creep and the time to fracture is approximately equal to the accumulated residual strain [3]. The dependences of the deformation activation energy (DAE) and specific FAE of metal alloys on stress are identical for different types of the stress–strain state [5], which is confirmed by data obtained for aluminum alloys [7, 10].

The form of the expression for the plastic strain rate is similar to that of Eq. (1):

$$\dot {\varepsilon }_p = \dot {\varepsilon }_0 \exp\Big( - \frac{Q_0 - \alpha \sigma }{RT}\Big).$$

(2)

Here $Q_0-\alpha \sigma$ is the deformation activation energy; the activation parameter $Q_0$ and activation volume $\alpha$ in the case of changes in the material structure induced by relaxation processes almost coincide with the activation parameter $U_0$ and activation volume $\gamma$ [10]. The pre-exponent $\dot {\varepsilon }_0 = \varepsilon _ * \nu _0$ in Eq. (2) depends on the material structure and can be expressed via the strain $\varepsilon _ *$, which depends on the activation entropy and on the distribution of deformation processes over the material volume [11, 12]. Therefore, in view of the interrelationship of the deformation and fracture processes (DAE and FAE), it is possible to develop mathematical models transforming external actions on the material to the kinetics of internal thermodynamic processes. In other words, the experimentally observed strength and deformation properties of materials can be determined in calculations by reproducing the governing processes in the models.

MATHEMATICAL MODELING OF RHEOLOGICAL PROPERTIES OF THE MATERIAL

New rheological models of material proposed in [12] were developed with the use of the Zhurkov plastic solid (Zh), Kauzmann solid (Km), and Hooke elastic solid (H). Figure 2 shows the one-dimensional model of the solid ($M,M_1,\dots,M_{n}$ are the elasticity moduli of the Hooke solids).

Fig. 2

Structural model of the material with in-series and parallel connections of the elastic solid (Hooke solid) and plastic flow solid (Zhurkov or Kauzmann solid).

Representing the plastic strain rate (2) at a constant temperature in the form $\dot {\varepsilon }_p =A\mathrm{e}^{B\sigma}$ for the Zh solid or $\dot {\varepsilon }_p = 2A\sinh\,(B\sigma)$ for the Km solid with in-series connection of these solids with the Hooke solid (PM$_1$ and PM$_{5}$ solids), we obtain the differential equations of their deformation [12]:

$$\frac{1}{M}\,\frac{d\sigma }{dt} + A\mathrm{e}^{B\sigma} = \frac{d\varepsilon}{dt}$$

(3)

or

$$\frac{1}{M}\,\frac{d\sigma }{dt} + 2A\sinh\,(B\sigma ) = \frac{d\varepsilon }{dt}.$$

(4)

For a constant total strain rate $d\varepsilon / dt = C$, we obtain solutions of Eqs. (3) and (4). For example, the solution of Eq. (3) has the form

$$\sigma = - \frac{1}{B}\ln \Big\{\mathrm{e}^{- B(\sigma _0 + MCt)}{} +\frac{A}{C}\,[1 - \mathrm{e}^{- BMCt}]\Big\}.$$

(5)

For a constant loading rate $d\sigma / dt = D$, the solution of Eq. (3), which is the dependence of strain on time, takes the form

$$\varepsilon = \varepsilon _0 + \frac{Dt}{M} + A\mathrm{e}^{B\sigma _0}\, \frac{\mathrm{e}^{BDt} - 1}{BD},$$

(6)

where $\sigma _0$ and $\varepsilon _0$ are the stresses and strains at the time $t = 0$.

Fig. 3

Stress versus strain for the PM$_1$ solid under the conditions of a constant strain rate (curve 1) and loading rate (curve 2).

If solutions (5) and (6) are constructed in the coordinates $\sigma$–$\varepsilon$, it can be easily demonstrated that one differential equation of deformation of an elastic solid connected to the plastic flow (creep) solid corresponds to two “plasticity theories." As $t \to \infty$, solution (5) yields the flow stress (yield stress)

$$\sigma = - B^{-1}\ln\,(A/C),$$

(7)

which depends on the strain rate and temperature. Figure 3 shows the stress as a function of strain for the PM$_1$ solid whose parameters correspond to the D16 T material with the mass fractions of (3.8–4.9%) Cu, (1.2–1.8%) Mg, and (0.3–0.9%) Mn with Fe, Si, Zn, Ti, and Ni admixtures (analog of the 2024 alloy in the ASTM standard) at $T=450$ K. The strain at points $A$ and $B$ is $\varepsilon = 1.024\%$. By fixing the material strain reached, one can calculate the stress relaxation by the following formula [12]:

$$\sigma = - B^{-1}\ln\,(\mathrm{e}^{- B\sigma _0}{} + ABMt).$$

Figure 4 shows the relaxation curves after reaching a certain value of stress for a constant strain rate and loading rate. After that, the relaxation process occurs without the work of external forces, i.e., owing to internal energy of the solid whose measure is the temperature [4]. The fracture rate can be changed only by external addition of energy, which changes the internal energy of the solid, or by material heating induced by the work of external forces (e.g., in the case of cyclic loading) [2].

Fig. 4

Time evolution of stress for the PM$_1$ solid under the conditions of a constant strain rate (curve 1) and loading rate (curve 2).

It is also possible to construct other structural models of the material with parallel connection of elastic and plastic solids, which describe deformations of another type characterizing the inelastic behavior of the material: unsteady stage of creep, plasticity with hardening, and hysteresis of inelastic deformation under cyclic loading.

The results of torsion tests of aluminum wire at different temperature values were reported in [13]. Let us consider the data obtained at $T = 448$ K. The specimen was subjected to the action of torque for a certain time interval, and then the loading was released. The torsion angle was registered on the basis of the light beam deviation. The thus-measured strain represented the elastic strain, strain corresponding to the initial stage of creep, and strain corresponding to creep recovery after unloading.

A reasonably accurate description of the process is ensured by the PM$_{10}$ rheological model [6], which implies in-series connection of the PM$_{5}$ solid ($\mathrm{PM}_5= \mathrm{H}-\mathrm{Km}$) and PM$_{6}$ solid ($\mathrm{PM}_6 = \mathrm{H}_1 \mid \mathrm{Km}_1$) [12], corresponding to two structural elements of the material model with the parameters $A$, $B$, $M$ and $A_1$, $B_1$, $M_1$(see Fig. 2). The signs “$-$" and “$\,\mid\,$" in the rheological formulas of the solids are used to indicate the in-series and parallel connections of solids, respectively.

The creep recovery curve is fairly accurately described by the equation of the rheological solid PM$_{6}$ in the entire interval of registration. The creep recovery process is described by the formula [6]

$$\varepsilon_\mathrm{rec} = \varepsilon_\mathrm{res}-\frac{2}{B_1 M_1 } {\mathrm{artanh}}\Big[\tanh\Big(-\frac{B_1 M_1 \varepsilon_0}{2}\Big) \mathrm{e}^{-2A_1 B_1M_1 t}\Big],$$

(8)

where $\varepsilon_{\mathrm res}$ is the residual (irreversible) creep strain accumulated during the time when the material was subjected to loading.

According to the data [13], the light beam was deflected from its initial position by 0.1 cm after five hours. The calculation by Eq. (8) shows that the beam deviation reaches 0.09 cm if the specimen is kept without loading for more than five hours. If the chosen parameters of the PM$_{6}$ solid are used to describe the initial period of the flow, then the model $\mathrm{PM}_{10} = \mathrm{PM}_5-\mathrm{PM}_6$ reproduces this period with reasonable accuracy as well. Under the assumption that the irreversible strain of the Km solid in the PM$_{5}$ element increases with a constant rate $\dot {\varepsilon }_c$, the expression for the plastic strain has the form

$$\varepsilon_p = \dot {\varepsilon}_c t + \frac{1}{M_1} \Big\{\sigma_0-\frac{2}{B_1}\mathrm{artanh}\Big[\tanh\Big(\frac{B_1 \sigma_0 }{2}\Big) \mathrm{e}^{-2A_1 B_1 M_1 t}\Big]\Big\},$$

(9)

where $\dot {\varepsilon }_c = \varepsilon _{\mathrm res} / t$.

Fig. 5

Time evolution of the light beam deflection $\Delta$ from its initial position in the torsion test of aluminum wire at $T=448$ K: the creep region and creep recovery region are indicated by 1 and 2, respectively.

The results calculated by formulas (8) and (9) are shown in Fig. 5. The parameters involved into Eqs. (8) and (9) were determined with the use of the experimental data [13]. The reversible component of creep can be also described by the rheological model of relaxation-type inelasticity by representing the recovery process as the sum of the exponents [6]. The description of the process by one expression (8) or (9) testifies that this is a local plastic flow rather than a viscous flow (as was assumed in [13]), whose activation energy is independent of stresses. In this case, the rheological model takes into account the inhomogeneity of the structure of the material specimen as a result of superposition of external and internal strain fields.

Let us now discuss the results of the experiment that differs from the experiment [13] by the absence of irreversible residual strain. The ring-shaped specimen made of superhigh-molecular polyethylene (SHMPE) containing SiC particles (the mass fraction of particles was 20%, the outer diameter of the specimen was 95 mm, the inner diameter of the specimen was 47.5 mm, and the thickness was 9.3 mm) was loaded by cyclic compression between two plane–parallel supports. The compression force $P = (900\pm 700)$ N was applied with a frequency of 1 Hz at the temperature $T = 285$ K. In accordance with the solution of the elastic problem, the greatest compressive stresses at the internal contour of the ring at this load were $\sigma_\mathrm{compr}=(-11.40\pm 8.85)$ MPa, and the greatest tensile stresses were $\sigma_\mathrm{tens}=(12.9\pm 10.0)$ MPa. After 483 500 loading cycles, there were no signs of fracture despite the fact that local plastic deformation did occur, as evidenced by the amplitude dependence of inelasticity under cyclic loading. It was only the specimen shape that changed and became elliptical; however, the shape started gradually to recover after the load was removed. In the course of recovery, the ring diameter was measured for 53 days at $T = 293$ K (Fig. 6). The calculations were performed by Eq. (8) whose parameters were chosen in accordance with the ring size at points 1–3. The calculated curve also passes through the experimental points 4–6 under the condition that $\varepsilon_{\mathrm res}= 0$ in Eq. (8). Thus, it can be expected that the ring size is completely recovered after a sufficiently long time. As in the example considered above, the rheological model takes into account the inhomogeneity of the material specimen structure arising due to superposition of external and internal strain fields, but at another stress–strain state.

Fig. 6

Change in the SHMPE ring diameter in the force action direction: reduction of the ring diameter in the course of cyclic compression (from point 0 to point1) and recovery of the ring diameter after load removal (from point 1 to point 6).

Fig. 7

Disclosure of the inelasticity loop of the ring-shaped SHMPE specimen versus the loading amplitude for the loading frequency $f = 1$ Hz ($T= 285$ K): relaxation-type inelasticity (1) and inelasticity of the relaxation and hysteresis types (2).

One structural element PM$_6$ was used in simulations in both examples considered here. For determining the contributions of other elements in parametric identification of the structural model of the material, we construct the amplitude dependence of the degree of disclosure of the inelasticity loop. The degree of disclosure of the inelasticity loop was calculated for the mean value of the force or stress in the loading cycle as the difference of displacements or strains under loading and unloading. Figure 7 shows the amplitude dependence of the loop disclosure $dS$ of the SHMPE specimen before the tests with cyclic compression. The abscissa axis is the stress defined as the force divided by the area of the diametral cross section of the ring.

Internal friction of the relaxation type is observed for all materials at low amplitudes of loading [14]. Curve 1in Fig. 7 starts from the origin of the coordinate system. If the areas of the inelasticity loops are calculated, the resultant dependence on the squared amplitude is also linear. The deviation of the curve $dS(\sigma_a)$ from zero at $\sigma_a = 0$ is 11 $\mu$m. This deviation is caused by the experimental error and by the discreteness of digitization of the signal of the displacement sensor of the test machine ($\pm5.8$ $\mu$m). For low loading amplitudes, a typical feature for any material is the delay of strains from stresses in phase. However, fatigue fracture usually does not occur if the material structure contains no point defects [6]. If this type of inelastic deformation has to be described in the models (e.g., in the case of vibrations), the structural model illustrated in Fig. 2 should be supplemented with the Kelvin (Voigt) element or a similar set of such elements characterizing the spectrum of relaxation processes [14].

As the loading amplitude is increased, curve 2 in Fig. 7 deviates from curve 

1, which testifies to the presence of local plastic deformations in the material structure. The increase in the slope of the segments of curve 2 (piecewise-linear dependence) testifies to enhancement of the hysteresis-type inelasticity, which should be modeled by the structural elements of the material model. Apparently, enhancement of inelasticity on each segment is caused by the emergence of new local volumes in the material structure where the internal stresses have reached significant values. Clearly, the stress relaxation rate in volumes with different initial value of internal stresses is also different (see, e.g., Fig. 4). In the examples considered here, one structural element of the model was sufficient to describe the long-time process of inelastic deformation recovery in the examples considered here owing to moderate values of internal stresses.

If the stress sign is changed, the absolute value of the stress should be used in Eq. (2) and the sign of the rate should be changed to the opposite sign, but this should be done only if the material behaves identically in tensile and compressive tests. Otherwise, the parameters $A$ and $B$ should be changed (as it is done in the case of composites). Concerning the damage accumulation process, it depends on the material used. For example, damage accumulation does occur under cyclic compression of metal alloys, but this process has a decaying character [6]. Fracture of composite materials under the action of compressive loads is similar to fracture of metal alloys under tension [15].

PREDICTION OF DEFORMATION AND STRENGTH PROPERTIES OF MATERIALS UNDER VARIOUS TEMPERATURE AND FORCE CONDITIONS

As the temperature is explicitly involved into Eqs. (1) and (2), the processes of deformation and failure at variable temperatures and stresses can be easily described.

As inelastic deformation in the case of variable loads is related to local plastic strains accompanying fatigue failure of the material, it is possible to use the same relationship (as that in the case of creep) between the deformation and failure processes for local volumes for determining the longevity for arbitrary external loading conditions. By means of calculations, it is possible to demonstrate which structural element of the material model is responsible for its longevity and fracture of which type will occur: due to fatigue or creep [6].

Specimens made of the AK4-1 T1 alloy with the mass fractions of (1.9–2.5%) Cu, (1.4–1.8%) Mg, (0.8–1.3%) Fe, (0.8–1.3%) Ni, 0.35% Si, and (0.02–0.10%) Ti; Zn and Mn admixtures (analog of the 2618 alloy in ASTM standard) were tested at a temperature $T = 543$ K and loading frequency of 10 Hz [6]. The calculation was performed with the use of the structural model of this material including only the Hooke and Zhurkov solids (PM$_1$ in Fig. 2). The calculated and experimental data are summarized in Table 1. Though the predicted values of longevity are within the scatter of the experimental data, they are closer to the maximum values. At $T = 543$ K, fatigue fracture is not expected to occur, but these specimens had deviations in terms of thermal treatment, and the activation volume estimated in subsequent tests had a greater value [6].

Table 1. Results of testing specimens 15 mm in diameter and 60 mm long made of the AK4-1 T1 alloy at $T=543$ K

In the case of simultaneous changes in temperature and stresses with comparable rate of changing of these quantities, it is possible to use an approximate solution at a time step. Let the flow velocity at the beginning and end of the time step be

$$\dot {\varepsilon }_{p1} = \varepsilon _ * \nu _0 \exp\Big( - \frac{Q_0 - \alpha _1 \sigma _1 }{RT_1 }\Big),\qquad \dot {\varepsilon }_{p2} = \varepsilon _ * \nu _0 \exp\Big( - \frac{Q_0 - \alpha _2 \sigma _2 }{RT_2 }\Big).$$

The change in the plastic strain rate at the time step $\Delta t$ can be presented as

$$\dot {\varepsilon }_p = \tilde {A}\mathrm{e}^{\tilde {B} + \tilde {D}\,\Delta t}$$

assuming that the argument under the exponent sign changes in accordance with a linear law. Then, for example, for the plastic strain component in solution (6), integration yields

$$\Delta \varepsilon _p = \tilde {A}\mathrm{e}^{\tilde {B}}\, \frac{\mathrm{e}^{\tilde D\,\Delta t} - 1}{\tilde {D}}.$$

Table 2. Experimental and calculated longevity of a band with a longitudinal stringer ($K_{t} = 2.89$) made of the AK4-1 T1 alloy for different temperature and force loading conditions

Table 2 shows the results on the longevity of riveted specimens under thermomechanical loading, which was performed by the above-described algorithm, and also the experimental data [6]. The range of the experimental values of longevity corresponds to their actual scatter, while the range of the calculated values corresponds to the range of the range of experimental measurements of temperature

 ($\pm 5$ K) and load ($\pm 1\%$). The parameters in Table 2 are the temperature $T_{s}$ specified by the test program at the non-reinforced end of the band, the temperature in fracture regions (between the rivets in a double-row longitudinal joint) $T_{b}$, the nominal stresses $\sigma_{n}$, and the duration of the temperature-force cycle $t_{c}$. The numerical values calculated on the basis of the averaged statistical characteristics of several welding procedures are in reasonable agreement with the experimental data for material specimens from another lot.

Table 3. Experimental and calculated endurance of specimens made of a clad sheet of the 1201 AT1 alloy with the central orifice 20 mm in diameter with the cross-sectional size of $6\times 30$ mm ($K_{t} = 2.08$) tested at different frequencies and loading cycle shapes ($T = 293$ K)

The fact that fatigue fracture is a time-dependent process is confirmed by experiments performed at different loading frequencies. Specimens made of the 1201 T1 alloy with the mass fractions of (6–7%) Cu and (0.4–0.8%) Mn and with Zr, V, and Mg additives and Fe, Si, and Zn impurities (analog of the 2219 alloy in the ASTM standard) were tested at different values of the loading frequency and different loading cycle shapes [6]. The mean logarithmic values of endurance of these specimens $\langle N_{\lg}\rangle$ and the calculated values of longevity (the probability of fracture was taken to be 0.5) are listed in Table 3. The calculations were performed with the use of the effective coefficient of strain concentration $K_f = 1 + q(K_t-1)$($K_t$ is the theoretical coefficient of strain concentration). The parameter $q$ depends on the material quality, type of the billet, and technology of specimen fabrication [6].

Fig. 8

Endurance $N$(points 1 and  2) and longevity $\tau$(points 3 and  4) of specimens (see Table 3) versus the loading frequency for the case of harmonic variation of the load: experiment (1 and 3), calculation (2 and 4), and approximation of the experimental data 1 and3 (curves 5 and 6, respectively).

As the inelastic strain of the material in the loading cycle depends on the local stress of the flow, which is determined by Eq. (7) in the model, and changes proportionally to the change in the loading rate logarithm, the frequency dependence of endurance has to take this dependence into account. At the same time, minor changes in the inelastic strain induced by frequency variation are expected to yield almost inversely proportional dependences of longevity on the loading frequency. Figure 8 shows the experimental and calculated dependences of endurance and longevity on the loading frequency. The approximating curves 5 and 6 are drawn through the points corresponding to the mean logarithmic values of endurance and longevity. Points 3 correspond to the actual scatter of longevity. Similar calculations can be also performed for another test temperature [6].

Thus, as the loading frequency is increased by a factor of 400, the endurance at this loading amplitude increases only by 23%, whereas the longevity decreases by a factor of 342.5. The factor of interest in exploitation of various structures is the longevity, i.e., the time of safe operation of the structure. The structure is usually affected by variable loads and also by variable temperatures in some cases. If the kinetic concept of fracture is used, the methods of calculating the longevity estimates are not principally different from the methods used in the case of cyclic loading; these methods were described in [6].

In each case, the structures are loaded in a different way; therefore, obtaining estimates requires statistical data on the typical operation conditions. Calculations are performed with averaged statistical data on loading, i.e., the mean spectral density of the processes, which is then transformed to a discrete spectrum by the method of summation of elementary random functions [6]. As a result, one obtains a pseudo-random process (PRP), which is statistically equivalent to a real random process. Let us compare the experimental and calculated longevity values for different PRPs that refer to the same unsteady random process.

Fig. 9

Calculated values of longevity $\tau_{c}$ obtained for different loading spectra and experimental mean logarithmic values of longevity $\tau_{e}$ of specimens made of the 1201 T1 alloy: (1) real loading spectrum ($\sigma_m=100$ MPa); (2) PRP with 67 harmonics ($\sigma_m=100$ MPa); (3) PRP with 23 harmonics ($\sigma_m=100$ MPa); (4) real loading spectrum ($\sigma_m=0$); (5) PRP with 67 harmonics ($\sigma_m=0$); (6) PRP with 23 harmonics ($\sigma_m=0$); (7) PRP with 13 harmonics ($\sigma_m=100$ MPa); (8) PRP with 13 harmonics ($\sigma_m=0$); (9) PRP with 62 harmonics ($\sigma_m=0$).

Specimens cut out from a plate made of the 1201 T1 alloy (with the cross-sectional size of $4.5\times 30.0$ mm) and containing the central orifice 5 mm in diameter were tested with the use of the BiSS 100 kN (Bangalore Integrated System Solutions) and MTS-10 test machines. The experimental load was the bending moment acting to the wing of a cargo airplane during its landing. Figure 9 shows the calculated and experimental values of the longevity of specimens tested in different modes of loading for two values of the mean stress $\sigma_{m}$ and root-mean-square deviation of 47 MPa from the value of $\sigma_{m}$. The calculation was performed with the effective coefficient of fatigue strain concentration $K_{f}$ corresponding to the billet material quality and with allowance for the material creep at points located on the orifice contour [10].

Points 2, 3, 5, and 6 in Fig. 9 correspond to loading with the same spectrum of real loads in the frequency range $f = 0.08-16.00$ Hz, and points 7 and  8 refer to the spectrum of narrowband random noise in the loading frequency range $f =0-5.5$ Hz [6]. Moreover, an experiment was performed (point 9), where the spectrum was represented by harmonics distributed over the frequency logarithm. In this way, the variance of the process at low frequencies of the spectrum could be described in more detail. To determine the longevity as a function of the characteristics of discreteness and frequency composition of the spectra, the values of the root-mean-square deviation and $\sigma_{m}$ were chosen to be identical.

The difference in the spectra can be formulated as follows. In the case with 13 harmonics, the frequency range in the spectrum of narrowband random noise is bounded by the frequency $f = 5.5$ Hz. In the case with 62 harmonics distributed over the frequency logarithm, the high-frequency part of the spectrum is also represented by a moderate number of elementary random functions. Therefore, despite the small value of the variance in the high-frequency part of the loading spectrum, its effect on longevity is fairly significant. An appreciable difference in the longevity values (point 8) even if there are few harmonics in the representation of the high-frequency part of the spectrum (point 9).

As follows from Fig. 9, the predicted values of longevity for the fracture probability taken to be equal to 0.5 are in reasonable agreement with the experimental data in all cases. In the existing approaches based on the concept of a cycle, the real random process is schematized, resulting in distortion of the initial information about the process.

CONCLUSIONS

Using the kinetic concept of fracture based on the reaction rate theory, the strength and deformation characteristics of materials subjected to different types of loading are analyzed. A method for predicting the longevity of structural materials based on reproduction of internal thermodynamic processes of deformation, fracture, and structural changes in materials determining their mechanical characteristics is described. The proposed approach allows one to estimate the behavior of structural materials subjected to arbitrary thermal and force actions by using a unified algorithm of calculations.