INTRODUCTION

The problem of interaction between two solid spheres (with constant radii) in a viscous fluid in the Stokes approximation was first considered in the exact formulation in [1], where spheres moved along their centerline and the fluid flow was assumed to be axisymmetric. For the stream function, an expansion in Gegenbauer polynomials in bispherical coordinates was constructed. This function was used to obtain infinite series expansions for the viscous forces acting on the spheres, which were later used to determine the main asymptotics of viscous forces at large distances from the contact zone of the spheres [2] and near this zone [3, 4]. In [3–5], the main asymptotics of the forces near the contact zone of the spheres were found using lubricating layer theory.

The problem of the interaction between two solid spheres has also been solved using the method of reflections [6]. In [6], an expansion of viscous forces at large distances was derived, and the interaction force arising from the motion of two spheres with constant radii and the same velocities in the contact zone was found. Series obtained by the method of reflections converge much faster than expansions in inverse powers of the distance \(r\) between the centers of the spheres. However, this is insufficient for analyzing the approach of bubbles [7].

The purpose of this work is, using the method of [1], to obtain the exact solution of the problem of viscous interaction between two spheres with arbitrary variable radii under the no-slip condition on the surfaces of the spheres. Infinite series expressions for viscous forces are used to obtain their asymptotic expansions near the contact zone.

Fig. 1
figure 1

Formulation of the problem.

Full size image

1. FORMULATION OF THE PROBLEM

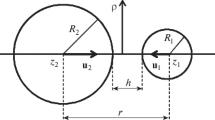
The interaction between two spherical bubbles with variable radii moving in a viscous fluid along their centerline is considered in the Stokes approximation. The fluid flow is assumed to be axisymmetric. The centers of the spheres located on the \(z\) axis have coordinates \(z_1\) and \(z_2\)(\(z_1>z_2\)), and the velocities of the centers are \(u_1=-\dot{z}_1\), \(u_2=\dot{z}_2\) and are directed toward each other (see the figure). The rates of change of the radii are \(\dot{R}_1\) and \(\dot{R}_2\), respectively. The distance between the centers of the spheres is \(r=z_1-z_2\), and the distance between the surfaces of the spheres (gap) is \(h=r-R_1-R_2\). It is required to find the viscous friction forces acting on the spheres as linear functions of \(u_1\), \(u_2\)\(\dot{R}_1\), and \(\dot{R}_2\), whose coefficients depend on the radii of these spheres and the distance between them.

According to [1], it is reasonable to seek the solution of the problem using the Stokes stream function in bispherical coordinates, which must satisfy the equation [1]

$$\Phi^4(\psi)=0;$$
$$\Phi^2\equiv \frac{\cosh \xi -\mu}{c^2} \Big(\frac{\partial}{\partial \xi} \Big((\cosh \xi -\mu)\,\frac{\partial}{\partial \xi}\Big) +(1-\mu^2)\,\frac{\partial}{\partial \mu} \Big( (\cosh \xi -\mu)\,\frac{\partial}{\partial \mu}\Big)\Big).$$
(1)

The bispherical coordinates \(\xi\), \(\zeta\), and \(\theta\) are related to the Cartesian coordinates as follows:

$$\rho =c\,\frac{\sin \zeta }{\cosh \xi -\cos \zeta }, \qquad z=c\,\frac{\sinh \xi }{\cosh \xi -\cos \zeta }, \quad x=\rho \cos \theta,\quad y=\rho \sin \theta.$$

Furthermore, the surfaces of the spheres are given by the equations (see the figure)

$$\xi =(-1)^{i-1} \tau_i=\mathrm{const},\qquad \zeta \in [0,\pi ],\quad \theta \in [0,2\pi ],\quad i=\{1,2\},$$

and the parameters \(\tau_1\), \(\tau_2\), and \(c\) are found from the equations

$$R_1\sinh \tau_1=c, \qquad R_2\sinh \tau_2=c,\qquad r=R_1\cosh\tau_1+R_2\cosh\tau_2.$$

2. STREAM FUNCTION IN BISPHERICAL COORDINATES

We will seek the stream function in the form [1]

$$\psi =(\cosh \xi -\cos \zeta)^{-3/2} \sum\limits_{n=0}^{\infty } U_n(\xi)C_{n}^{-1/2}(\cos \zeta ),$$
$$U_n(\xi )=a_n\cosh\,(n-3/2)\xi+b_n\sinh\,(n-3/2)\xi +c_n\cosh\,(n+1/2)\xi +d_n\sinh\,(n+1/2)\xi,$$
(2)

where \(C_{n}^{-1/2}(\mu )\)(\(n=0,1,2,\dots\)) are Gegenbauer polynomials [8]. When solving the problem for spheres with variable radii, the summation should be started from \(n=0\), since, in this case, the set of Gegenbauer polynomials forms a complete basis [9].

The coefficients \(a_n\), \(b_n\), \(c_n\), and \(d_n\) are found from the boundary conditions on the surfaces of the spheres for \(\xi =\tau_1\) and \(\xi=-\tau_2\). In the case of a viscous fluid, in addition to the condition for the normal velocity component, we specify the second condition for the tangential velocity or for the shear stress. In this paper, we consider the case of no-slip at the bubble boundary. This condition is natural in the presence of surfactants in various gas–liquid technologies.

3. BOUNDARY CONDITIONS

We formulate the boundary conditions on the surfaces of the spheres.

3.1. Normal Component

The normal component of the fluid velocity \(v_n\) and the bubble surface velocity \(w_n\) should coincide: \((\boldsymbol{v}_1,\boldsymbol{n})=(\boldsymbol{w}_1,\boldsymbol{n})\) on the boundary of the first sphere and \((\boldsymbol{v}_2,\boldsymbol{n})=(\boldsymbol{w}_2,\boldsymbol{n})\) on the boundary of the second sphere. In bispherical coordinates, the scalar products \((\boldsymbol{v}_{i},\boldsymbol{n})\), \((\boldsymbol{w}_i,\boldsymbol{n})\) are given by the formulas

$$(\boldsymbol{v}_1,\boldsymbol{n})=\frac{1}{\rho }\,\frac{\partial \psi }{\partial \zeta }\, \frac{\cosh\tau_1-\cos \zeta }{c},\qquad (\boldsymbol{w}_1,\boldsymbol{n})=-u_1\Big( -\frac{\cosh {\tau_1}\cos \zeta -1} {\cosh {\tau_1}-\cos \zeta } \Big)-\dot{R}_1,$$
$$(\boldsymbol{v}_2,\boldsymbol{n})=\frac1{\rho }\,\frac{\partial \psi }{\partial \zeta }\, \frac{\cosh \tau_2-\cos \zeta }{c}, \qquad (\boldsymbol{w}_2,\boldsymbol{n})=u_2\Big( -\frac{\cosh {\tau_2}\cos \zeta -1}{\cosh {\tau_2}-\cos \zeta } \Big) +\dot{R}_2.$$
(3)

Integrating the boundary conditions (3) over \(\zeta\) and choosing the integration constants in such a way that, on the axis of symmetry, the velocity vector is parallel to this axis, we obtain

$$\psi\big|_{\xi =\tau_1}= u_1c^2\,\frac12\,\frac{1-\mu^2}{(\cosh \tau_1-\mu)^2} +\dot{R}_1c^2\,\frac{1}{\cosh\tau_1-\mu } +\Big(\frac{\dot{R}_2c^2}{\sinh^2\tau_2} -\frac{\dot{R}_1c^2\cosh\tau_1}{\sinh^2\tau_1}\Big),$$
$$\psi\big|_{\xi =-\tau_2}=-u_2c^2\,\frac12\,\frac{1-\mu^2} {(\cosh\tau_2-\mu)^2}-\dot{R}_2c^2\,\frac1{\cosh\tau_2-\mu} -\Big(\frac{\dot{R}_1c^2}{\sinh^2\tau_1} -\frac{\dot{R}_2c^2\cosh\tau_2}{\sinh^2\tau_2}\Big).$$
(4)

Taking into account the form of the stream function (2), we transform conditions (4) to

$$\sum\limits_{n=0}^{\infty }U_n(\tau_1)C_n^{-1/2}(\cos \zeta)-f_0(\mu)=0,\qquad \sum\limits_{n=0}^{\infty }U_n(-\tau_2)C_n^{-1/2}(\cos \zeta )-g_0(\mu)=0,$$
(5)

where

$$f_0(\mu)=u_1c^2\,\frac12\,\frac{1-\mu^2}{(\cosh\tau_1-\mu)^{1/2}} +\dot{R}_1c^2(\cosh\tau_1-\mu)^{1/2} +\Big(\frac{\dot{R}_2c^2}{\sinh^2\tau_2} -\frac{\dot{R}_1c^2\cosh\tau_1}{\sinh^2\tau_1}\Big) (\cosh\tau_1-\mu)^{3/2},$$
$$g_0(\mu)=-u_2c^2\,\frac12\,\frac{1-\mu^2}{(\cosh\tau_2-\mu)^{1/2}} -\dot{R}_2c^2(\cosh\tau_2-\mu)^{1/2} -\Big(\frac{\dot{R}_1c^2}{\sinh^2\tau_1} -\frac{\dot{R}_2c^2\cosh\tau_2}{\sinh^2\tau_2}\Big) (\cosh\tau_2-\mu)^{3/2}.$$
(6)

Next, we expand the functions \(f_0(\mu)\) and \(g_0(\mu)\) in terms of the Gegenbauer polynomials as follows.

According to [1, 8], for \(\tau>0\), \(-1 \leq \mu \leq 1\), the following identities hold:

$$(\cosh \tau-\mu)^{1/2}=\sum\limits_{n=0}^{\infty } C_{n}^{-1/2}(\mu )\,\frac{\sqrt2}{2}\,\mathrm{e}^{-(n-1/2)\tau},$$
$$\frac{1}{(\cosh \tau-\mu)^{1/2}} =\sum\limits_{n=0}^{\infty }C_{n}^{-1/2}(\mu )\, \frac{-(n-1/2)\sqrt2}{\sinh \tau}\,\mathrm{e}^{-(n-1/2)\tau},$$
$$(\cosh \tau-\mu)^{3/2}=\sum\limits_{n=0}^{\infty } C_{n}^{-1/2}(\mu )\,\frac{3 \sqrt2}{8} \Big(\frac{\mathrm{e}^{-(n+1/2)\tau}}{n+1/2} -\frac{\mathrm{e}^{-(n-3/2)\tau}}{n-3/2} \Big),$$
$$\frac{1-\mu^2}{(\cosh \tau-\mu)^{3/2}} =\sum\limits_{n=0}^{\infty } C_{n}^{-1/2}(\mu )2\sqrt2\,n(n-1) \mathrm{e}^{-(n-1/2)\tau},$$
$$\frac{1-\mu^2}{(\cosh \tau-\mu)^{1/2}} =\sum\limits_{n=0}^{\infty }C_{n}^{-1/2}(\mu )\, \frac{\sqrt2}{2}\,n(n-1)\Big(\frac{\mathrm{e}^{-(n-3/2)\tau}}{n-3/2} -\frac{\mathrm{e}^{-(n+1/2)\tau}}{n+1/2}\Big).$$

3.2. Tangential Component

If the no-slip condition on the boundary is satisfied, the tangential velocity components are \(v_\tau=w_\tau\)\([(\boldsymbol{v}_1,\boldsymbol\tau)=(\boldsymbol{w}_1,\boldsymbol{\tau})\) on the boundary of the first sphere and \((\boldsymbol{v}_2,\boldsymbol\tau)=(\boldsymbol{w}_2,\boldsymbol\tau)\) on the boundary of the second sphere]. In bispherical coordinates, the scalar products \((\boldsymbol{v}_i,\boldsymbol{\tau})\) and \((\boldsymbol{w}_i,\boldsymbol\tau)\) are given by the formulas

$$(\boldsymbol{v}_1, \boldsymbol{\tau})=-\frac1{\rho }\,\frac{\partial \psi }{\partial \xi }\, \frac{\cosh {\tau_1}-\cos \zeta }{c},\qquad (\boldsymbol{w}_1, \boldsymbol{\tau})=u_1\,\frac{\sinh {\tau_1}\sin \zeta }{\cosh {\tau_1}-\cos \zeta },$$
$$(\boldsymbol{v}_2, \boldsymbol{\tau})=-\frac1{\rho }\,\frac{\partial \psi }{\partial \xi }\, \frac{\cosh {\tau_2}-\cos \zeta }{c}, \qquad (\boldsymbol{w}_2, \boldsymbol{\tau})=u_2\,\frac{\sinh {\tau_2}\sin \zeta }{\cosh {\tau_2}-\cos \zeta }.$$

Hence we have

$$\frac{\partial \psi }{\partial \xi }\Big|_{\xi=\tau_1} = -u_1 c^2\,\frac{\sinh \tau_1 (1-\mu^2)}{(\cosh \tau_1 -\mu)^3},\qquad \frac{\partial \psi }{\partial \xi }\Big|_{\xi=-\tau_2} = -u_2 c^2\, \frac{\sinh \tau_2 (1-\mu^2)}{(\cosh \tau_2 -\mu)^3}.$$
(7)

Using the stream function \(\psi\) (2), we obtain

$$\frac{\partial \psi }{\partial \xi } =(\cosh \xi -\mu)^{-3/2} \sum\limits_{n=0}^{\infty } U'_n (\xi) C_{n}^{-1/2}(\mu ) -\frac32\,\frac{\sinh \xi}{ \cosh \xi -\mu}\,\psi,\qquad U'_n (\xi) = \frac{\partial U_n(\xi)}{\partial \xi }.$$
(8)

Substitution of equality (8) into (7) yields the system of equations

$$\sum\limits_{n=0}^{\infty } U'_n(\tau_1) C_{n}^{-1/2}(\mu ) =\frac32\,\sinh \tau_1 (\cosh \tau_1 -\mu)^{1/2} \;\psi\big|_{\xi=\tau_1} -u_1 c^2\,\frac{\sinh \tau_1 (1-\mu^2)}{(\cosh \tau_1 -\mu)^{3/2}},$$
$$\sum\limits_{n=0}^{\infty }U'_n(-\tau_2)C_{n}^{-1/2}(\mu )= -\frac32 \sinh \tau_2 (\cosh \tau_2 -\mu)^{1/2}\;\psi\big|_{\xi=-\tau_2} -u_2 c^2\,\frac{\sinh \tau_2 (1-\mu^2)}{(\cosh \tau_2 -\mu)^{3/2}}.$$
(9)

Substitution of (4) into (9) yields

$$\sum\limits_{n=0}^{\infty }U'_n(\tau_1)C_{n}^{-1/2}(\mu )-f_1(\mu)=0,\qquad \sum\limits_{n=0}^{\infty }U'_n(-\tau_2)C_{n}^{-1/2}(\mu )-g_1 (\mu)=0,$$
(10)

where

$$\quad f_1 (\mu) = -u_1 c^2\,\frac14\,\frac{\sinh \tau_1 (1-\mu^2)}{(\cosh \tau_1 -\mu)^{3/2}} +\dot{R}_1c^2\,\frac32\,\frac{\sinh \tau_1}{(\cosh {\tau_1}-\mu)^{1/2}}{}$$
$${}+\Big(\frac{\dot{R}_2c^2}{\sinh^2\tau_2} -\frac{\dot{R}_1c^2\cosh\tau_1}{\sinh^2\tau_1}\Big) \frac32\,\sinh \tau_1 (\cosh \tau_1 -\mu)^{1/2},\quad$$
$$\quad g_1 (\mu) = -u_2 c^2\,\frac14\,\frac{\sinh \tau_2 (1-\mu^2)}{(\cosh \tau_2 -\mu)^{3/2}} +\dot{R}_2c^2\,\frac32\,\frac{\sinh \tau_2}{(\cosh {\tau_2}-\mu)^{1/2}}{}$$
(11)
$${}+\Big(\frac{\dot{R}_1c^2}{\sinh^2\tau_1} -\frac{\dot{R}_2c^2\cosh\tau_2}{\sinh^2\tau_2}\Big) \frac32 \sinh \tau_2 (\cosh \tau_2 -\mu)^{1/2}.\quad$$

Next, the functions \(f_1(\mu)\) and \(g_1(\mu)\) should be expanded in Gegenbauer polynomials as was done above.

The coefficients of the Gegenbauer polynomials \(C_{n}^{-1/2}\) in Eqs. (5), (10) must be equal to zero. Hence, for every four unknowns \((X_n)^{t} =\{ a_n,b_n,c_n,d_n\}\), we obtain the system of equations

$$M_n X_n-B_n=0, \qquad n=0,1,2, \dots,$$
(12)

where the matrix \(M_n\) is

$$M_n=\left(\begin{array}{cccc} c^{-}_{\tau_1} & s^{-}_{\tau_1} & c^{+}_{\tau_1} & s^{+}_{\tau_1}\\ c^{-}_{\tau_2} & -s^{-}_{\tau_2} & c^{+}_{\tau_2} & -s^{+}_{\tau_2}\\ n_{-}s^{-}_{\tau_1} & n_{-}c^{-}_{\tau_1} & n_{+} s^{+}_{\tau_1} & n_{+}c^{+}_{\tau_1}\\ -n_{-} s^{-}_{\tau_2} & n_{-}c^{-}_{\tau_2} & -n_{+} s^{+}_{\tau_2} & n_{+} c^{+}_{\tau_2} \end{array}\right),$$

\(n_{-}=n-3/2\), \(n_{+}=n+1/2\), \(c^{\pm}_{\xi} = \cosh n_{\pm} \xi\), and \(s^{\pm}_{\xi} = \sinh n_{\pm} \xi\); the column \(B_n\) is omitted due to its cumbersomeness.

Solving the system of linear equations (12), we obtain expressions for \(\{ a_n,b_n,c_n,d_n\}\), which are then used to determine the viscous forces and their asymptotics near the contact zone of the spheres.

4. EXPRESSIONS FOR VISCOUS FORCES

In [1], the following formula for the resulting force acting on each of the solid spheres was obtained:

$$F_{\mu_l}=\pi \mu_l \int \rho^3\,\frac{\partial }{\partial n} \Big(\frac{ \Phi ^2(\psi )}{\rho^2}\Big)\,ds.$$
(13)

Here \(n\) is the outward normal to the surface of the sphere; \(ds\) is a meridian element; \(\mu_l\) is the fluid viscosity; the integral is taken along the meridian of the corresponding sphere; the operator \(\Phi^2\) is given by formulas (1).

It is found that formula (13) is also valid for spheres with variable radii. Substituting the stream function (2), we obtain exact expressions for viscous forces:

$$F_{\mu_l1}=-\mu_l\,\frac{8\pi c\dot{R}_1}{\sinh^2\tau_1} +\frac{2\sqrt2\,\pi \mu_l}{c}\, \sum\limits_{n=2}^{\infty }(a_n+b_n+c_n+d_n),$$
$$F_{\mu_l2}=\mu_l\,\frac{8\pi c\dot{R}_2}{\sinh^2\tau_2} +\frac{2\sqrt2\,\pi \mu_l}{c}\, \sum\limits_{n=2}^{\infty }(a_n-b_n+c_n-d_n).$$
(14)

5. ASYMPTOTIC EXPRESSIONS FOR VISCOUS FORCES

A method for obtaining asymptotic series up to a constant is proposed in [7]. The infinite sum in the first equation (14) can be represented as

$$\frac{2 \sqrt2}{c}\;\sum_{n=2}^{\infty } (a_n + b_n+c_n + d_n) =\frac{2 \sqrt2}{c}\;\sum_{n=2}^{1/(\tau_1+\tau_2)} (a_n + b_n+c_n + d_n)+O(1).$$
(15)

For the finite sum in (15), we obtain an expansion in the small parameter \(\tau_1+\tau_2\):

$$\frac{2 \sqrt2}{c}\;\sum_{n=2}^{1/(\tau_1+\tau_2)} (a_n + b_n+c_n + d_n) = \sum_{n=2}^{1/(\tau_1+\tau_2)} \Big(\frac{384 n(n-1)R_1 R_2^3 (u_1+u_2+\dot{R}_1+\dot{R}_2)} {(2n-1)(2n-3)^2 (2n+1)^2 (R_1+R_2)^3 \tau_1^2}{}$$
$${}+ \frac{24 R_1 \dot{R}_1}{(2n+1)(2n-3) \tau_1} +\frac{32 n(n-1) R_1 R_2}{(2n-1)(2n-3)^2 (2n+1)^2 (R_1+R_2)^3 }{}$$
$${}\times\{(u_1+u_2)[3(4 n^2-4n+15)R_1^2 +3 (28n^2-28n-15)R_1 R_2 +(12n^2-12n+25)R_2^2]{}$$
$${}+ \dot{R}_1 [3(4n^2-4n+15)R_1^2 -9 (4n^2-4n-5)R_1 R_2 - (48n^2-48n-55)R_2^2]c{}$$
$${}+\dot{R}_2 [(12n^2-12n+25)R_2^2 -9 (4n^2-4n-5)R_1 R_2 -(48n^2-48n-75)R_1^2]\} + O( \tau_1+\tau_2) \Big).$$
(16)

Interchanging the subscripts 1 and 2 and changing the sign before the sum sign, we find a similar expression for the force \(F_{\mu_l 2}\).

Substituting (16) into (15) and then into (14) and taking into account that

$$\tau_1=\frac{R_2}{R_1+R_2}\,\sqrt{\frac{2h}{\bar{R}}}+O(h^{3/2}),\qquad \tau_2=\frac{R_1}{R_1+R_2}\,\sqrt{\frac{2h}{\bar{R}}}+O(h^{3/2}),$$
$$c=\sqrt{2h\bar{R}}+O(h^{3/2}), \qquad \bar{R} = R_1 R_2/(R_1+R_2),$$

we obtain the expansion of viscous forces near the contact zone of the spheres in the final form

$$F_{\mu_l1}\approx -F_{\mu_l 2}= -6\pi \mu_l \bar{R}^2\,\frac{\dot{h}}{h} -6\pi \mu_l \bar{R} \ln \Big( \frac{\bar{R}}{h}\Big) \Big(\frac15+\frac{R_1 R_2}{(R_1+R_2)^2}\Big) \dot{h} {}$$
$$\qquad{}-6\pi \mu_l \bar{R} \ln \Big( \frac{\bar{R}}{h}\Big) \Big( \frac{R_2(R_2+2R_1)}{(R_1+R_2)^2}\,\dot{R_1} +\frac{R_1(R_1+2R_2)}{(R_1+R_2)^2}\,\dot{R_2}\Big) +O(1)$$
(17)

.

In the case of constant radii (\(\dot{R}_1 = \dot{R}_2 =0\)), the expansions of viscous forces coincide with the expansions obtained in [4, 5].

For bubbles with variable radii,the main part of the asymptotic expression, proportional to the expression \(1/h\) in formula (17), was obtained in [7, 10] using lubricating layer theory. In [11], thin layer theory was used for the case of bubble growth near the wall to obtain a logarithmic singularity of the asymptotic expression

$$F_{\mu_l} = -6\pi \mu_l R_1 \dot{h} \Big(\frac{R_1}{h}+O\Big( \ln \frac{h}{R_1}\Big) \Big) +6\pi \mu_l R_1 \dot{R_1} \Big(\ln \frac{h}{R_1} + O(1)\Big).$$

For \(R_2 \to \infty\) in formula (17) we obtain a more exact expansion containing the logarithmic singularity at \(\dot{h}\):

$$F_{\mu_l} = -6\pi \mu_l R_1 \dot{h} \Big(\frac{R_1}{h}-\frac15 \ln \frac{h}{R_1} + O(1)\Big)+6\pi \mu_l R_1 \dot{R_1} \Big(\ln \frac{h}{R_1} + O(1)\Big).$$

At large distances between the centers of the spheres \(r\), the asymptotics of viscous forces (14) take the form

$$\frac{F_{\mu_l 1}}{6\pi \mu_l R_1}\approx u_1\Big( 1+\frac{9}{4}\,\frac{R_1R_2}{r^2}\Big) +\frac32\,u_2\,\frac{R_2}{r}+\frac32\,\dot{R}_1\,\frac{R_1^2R_2}{r^3} +\dot{R}_2\,\frac{R_2^2}{r^2},$$
$$-\frac{F_{\mu_l 2}}{6\pi \mu_l R_2}\approx u_2\Big(1+\frac{9}{4}\, \frac{R_1R_2}{r^2}\Big)+\frac32\,u_1\,\frac{R_1}{r} +\frac32\,\dot{R}_2\,\frac{R_2^2R_1}{r^3} +\dot{R}_1\,\frac{R_1^2}{r^2},$$

which for \(\dot{R}_1=\dot{R}_2=0\) agrees with the results of [6].

CONCLUSIONS

The motion of two spheres with variable radii in a viscous fluid is considered in the Stokes approximation. An exact expression for hydrodynamic interaction forces was found. A two-term expansion for these forces under the no-slip boundary conditions was obtained. The first term is proportional to \(1/h\), and the second term is proportional to \(\ln h\). The logarithmic asymptotics, which is essential for the study of bubble coalescence problems [7], was first obtained. For solid spheres, the logarithmic asymptotics agrees with the asymptotic expressions [4, 5]. In the case of the interaction between a sphere with a variable radius and a plane, the obtained the result agrees with the result of [10]. The obtained exact expression for the interaction forces can be used to obtain expansions in inverse powers of \(r\).

The author is grateful to A. G. Petrov for useful comments and fruitful discussions.

This work was performed within the framework of State Assignment No. AAAA-A20-120011690138-6.