Shadowing and Antishadowing in the Rescaling Model

Nuclear deep inelastic structure functions $F_{2}^{A}(x,{{Q}^{2}})$ as well as parton distribution functions in a nuclei are investigated in the framework of rescaling model. Our analysis is based on analytical expressions for quark and gluon densities in a proton derived at the leading order of QCD coupling. By fitting the rescaling parameters from the experimental data on $F_{2}^{A}(x,{{Q}^{2}}){\text{/}}F_{2}^{D}(x,{{Q}^{2}})$ ratio for several nuclear targets, we derive predictions for corresponding nuclear parton distributions and, thus, for shadowing and antishadowing effects.

1 INTRODUCTION

The study of deep inelastic scattering (DIS) of leptons on nuclei shows the appearance of a significant effect of nucleon interaction in the nucleus, which eliminates the naive idea of the nucleus as a system of quasi-free nucleons (see, for example, review [1–5]). This effect was first discovered [6] by the European Muon Collaboration (EMC) in the domain of valence quark dominance, therefore it was called the EMC effect. Influence of nuclear effects on parton distribution functions (PDFs) meets a lot of interest from both theoretical and experimental points of view. In particular, detailed knowledge of PDFs in a nuclei (nPDFs) is necessary for any theoretical description of $pA$ and AA processes studied at modern (LHC, RHIC) and future colliders (FCC-he, EiC, EicC, NICA).

Usually the nuclear modification factor, defined as a ratio of per-nucleon structure functions in nuclei $A$ and deuteron, $R = F_{2}^{A}(x,{{Q}^{2}}){\text{/}}F_{2}^{D}(x,{{Q}^{2}})$, or rather ratio of corresponding parton densities, is introduced and its behavior in the shadowing ($x \leqslant 0.1$), anti-shadowing ($0.1 \leqslant x \leqslant 0.3$), valence quarks and Fermi motion dominance regions ($0.3 \leqslant x \leqslant 0.7$ and $x \geqslant 0.7$, respectively) is investigated. Unfortunately, up to now there is no commonly accepted framework to describe this nuclear modification of PDFs in a whole kinematical range. Two main approaches are used by different groups at present. In the first, which is currently seems to be more popular, nPDFs are extracted from a global fit to nuclear data using some empirical parametrization of corresponding intitial parton densities. Then, numerical solution of Dokshitzer–Gribov–Lipatov–Altarelli–Parisi (DGLAP) equations [7–11] is applied to describe their QCD evolution (see review [12] and references therein). The second strategy is based on special nPDF models (see, for example, [13–19] and review [20]).

The aim of this work is to study the nuclear modification of DIS structure function (SF) ${{F}_{2}}(x,{{Q}^{2}})$ in the framework of the rescaling model [15–17]. The rescaling model is based on the assumption [18, 19] that the effective size of gluon and quark confinement in nucleus is greater than in a free nucleon. Within the framework of perturbative QCD this confinement rescaling predicts [15–19] that ordinary PDFs and nPDFs can be connected by simply shifting the values of the kinematic variable Q² (see also review [21]). Thus, the rescaling model demonstrates the features inherent in both approaches: there is the relationship between PDFs and nPDFs that arises as a result of shifting in the scale Q² and, at the same time, both PDFs and nPDFs obey the DGLAP equations. In a sence, the rescaling model corresponds to the first strategy with empirical nPDFs obtained from the corresponding PDFs by $x$-independent shift. Initially, it was proposed for the domain of valence quarks dominance and expanded recently to a low x range [22–25].

Our analysis is mainly based on the leading order (LO) analytical expressions [26] for proton PDFs valid at both low and intermediate x values. At low x, these formulas were obtained in the so-called double asymptotic scaling (DAS) approximation [27–32], which is related to the asymptotic behaviour of DGLAP evolution. Performing fit on the NMC data [33], we derive nPDFs at low and moderate x values ($x \leqslant 0.7$) for several nuclei targets and then investigate shadowing and anti-shadowing effects¹ for DIS SF ${{F}_{2}}(x,{{Q}^{2}})$ itself and for corresponding quark and gluon distribution functions. Main advantage of our approach is related with analytical solution of the DGLAP equations.

2 PROTON SF $F_{2}^{p}(x,{{Q}^{2}})$, QUARK AND GLUON DENSITIES

It is well known that the proton SF $F_{2}^{p}(x,{{Q}^{2}})$ at the leading order of QCD coupling can be presented in the simple form

$$F_{2}^{p}(x,{{Q}^{2}}) = \sum\limits_i e_{i}^{2}[{{f}_{{{{q}_{i}}}}}(x,{{Q}^{2}}) + {{f}_{{{{{\bar {q}}}_{i}}}}}(x,{{Q}^{2}})]{\kern 1pt} {\kern 1pt} ,$$

(1)

where ${{f}_{{{{q}_{i}}}}}(x,{{Q}^{2}})$ and ${{f}_{{{{{\bar {q}}}_{i}}}}}(x,{{Q}^{2}})$ are the quark and an-tiquark densities in a proton, respectively. In the four-flavor scheme (4FS), where b and t quarks are separated out (which will always be used below), we have [43]

$$F_{2}^{{ep}}(x,{{Q}^{2}}) = \frac{5}{{18}}{\kern 1pt} {{f}_{{SI}}}(x,{{Q}^{2}}) + \frac{1}{6}{{f}_{{NS}}}(x,{{Q}^{2}}),$$

(2)

where the singlet part ${{f}_{{SI}}}(x,{{Q}^{2}})$ contains the valence and sea quark parts ${{f}_{V}}(x,{{Q}^{2}})$ and ${{f}_{S}}(x,{{Q}^{2}})$:

$${{f}_{V}} = f_{u}^{V} + f_{d}^{V},\quad {{f}_{S}} = \sum\limits_{i = 1}^4 (f_{{{{q}_{i}}}}^{S} + f_{{{{{\bar {q}}}_{i}}}}^{S}),$$

$${{f}_{{SI}}} = \sum\limits_{i = 1}^4 ({{f}_{{{{q}_{i}}}}} + {{f}_{{{{{\bar {q}}}_{i}}}}}) = {{f}_{V}} + {{f}_{S}}.$$

(3)

The nonsinget part ${{f}_{{NS}}}(x,{{Q}^{2}})$ contains difference between the up and down quarks:

$$\begin{gathered} {{f}_{{NS}}} = \sum\limits_{q = u,{\kern 1pt} c} \text{[}{{f}_{q}}(x,{{Q}^{2}}) + {{f}_{{\bar {q}}}}(x,{{Q}^{2}})] \\ - \;\sum\limits_{q = d,{\kern 1pt} s} [{{f}_{q}}(x,{{Q}^{2}}) + {{f}_{{\bar {q}}}}(x,{{Q}^{2}})]{\kern 1pt} {\kern 1pt} . \\ \end{gathered} $$

(4)

Using the Q²-evolutions for large and small values of x (see [28–32, 44, 48]), the analytical expressions [26] for PDFs were constructed.²

2.1 Nonsinglet and Valence Parts

The nonsinglet and valence quark part ${{f}_{i}}(x,{{Q}^{2}})$, where $i = V$ or NS, can be represented in the form (see [26])

$$\begin{gathered} {{f}_{i}}(x,{{Q}^{2}}) = \left[ {{{A}_{i}}(s){{x}^{{{{\lambda }_{i}}}}}(1 - x) + \frac{{{{B}_{i}}(s){\kern 1pt} x}}{{\Gamma (1 + {{\nu }_{i}}(s))}}} \right. \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}} + \,{{D}_{i}}(s)x(1 - x)} \right]{{(1 - x)}^{{{{\nu }_{i}}(s)}}}, \\ \end{gathered} $$

(5)

where $\Gamma$ is the Riemann’s $\Gamma$-function,

$${{\nu }_{i}}(s) = {{\nu }_{i}}(0) + rs,\quad {{B}_{i}}(s) = {{B}_{i}}(0){{e}^{{ - ps}}},$$

$$p = r({{\gamma }_{{\text{E}}}} + \hat {c}),\quad r = \frac{{16}}{{3{{\beta }_{0}}}},\quad \hat {c} = - \frac{3}{4},$$

$${{A}_{i}}(s) = {{A}_{i}}(0){{e}^{{ - d(1 - {{\lambda }_{i}})s}}},\quad d(1 - {{\lambda }_{i}}) = \frac{{{{\gamma }_{{NS}}}(1 - {{\lambda }_{i}})}}{{2{{\beta }_{0}}}},$$

$$s = \ln \left[ {\frac{{{{\alpha }_{s}}(Q_{0}^{2})}}{{{{\alpha }_{s}}({{Q}^{2}})}}} \right],$$

(6)

and ${{\gamma }_{{\text{E}}}} \simeq 0.5772$ is the Euler’s constant, β₀ = 11 – $(2{\text{/}}3){{N}_{f}}$ is the LO QCD $\beta$-function, ${{N}_{f}} = 4$ is a number of active (massless) quarks and ${{\gamma }_{{NS}}}(n)$ is the LO NS anomalous dimension. The factors $Q_{0}^{2}$, ${{A}_{i}}(0)$, ${{B}_{i}}(0)$, and ${{\nu }_{i}}(0)$ are free parameters which can be determined from experimental data.³

We note that (5) is constructed as a combination of the small-x part proportional to ${{A}_{i}}(s)$, large-x asymptotics proportional to ${{B}_{i}}(s)$ and additional term $\sim {\kern 1pt} {{D}_{i}}(s)$, which is subasymptotics in both the regions. Dependence on scale Q² in (5) is given by (6). The Q²‑dependence of the magnitude ${{D}_{i}}(s)$ is determined by corresponding sum rules (see [26]). Everywhere below, we apply “frozen” treatment of the QCD coupling (see, for example, [54] and references therein), where ${{\alpha }_{s}}({{Q}^{2}}) \to {{\alpha }_{s}}({{Q}^{2}} + M_{\rho }^{2})$ with ${{M}_{\rho }} \sim 1$ GeV, that immediately leads to $s \geqslant 0$.

2.2 Sea and Gluon Parts

It was shown [26] that the sea and gluon parts can be represented as combinations⁴ of the ± parts:

$${{f}_{i}}(x,{{Q}^{2}}) = \sum\limits_{j = \pm } f_{i}^{j}(x,{{Q}^{2}}),$$

(7)

where $i = S$ or g and

$$\begin{gathered} f_{S}^{ - }(x,{{Q}^{2}}) = [{{A}_{q}}{{e}^{{ - {{d}_{ - }}s}}}{{(1 - x)}^{{{{m}_{{q, - }}}}}} \\ + \,{{D}_{ - }}(s)x(1 - x)](1 - x{{)}^{{{{\nu }_{ - }}(s)}}}, \\ \end{gathered} $$

(8)

$$\begin{gathered} f_{S}^{ + }(x,{{Q}^{2}}) = \frac{{{{N}_{f}}}}{9}\left( {{{A}_{g}} + \frac{4}{9}{{A}_{q}}} \right) \\ \times \,\rho {{I}_{1}}(\sigma ){{e}^{{ - {{{\overline d }}_{ + }}s}}}{{(1 - x)}^{{{{m}_{{q, + }}} + {{\nu }_{ + }}(s) + 1}}}, \\ \end{gathered} $$

(9)

$$\begin{gathered} f_{g}^{ - }(x,{{Q}^{2}}) = - \frac{4}{9}{{A}_{q}}{{e}^{{ - {{d}_{ - }}s}}}{{(1 - x)}^{{{{m}_{{g, - }}} + {{\nu }_{ - }}(s) + 1}}} \\ + \frac{{{{K}_{ - }}}}{{\Gamma (2 + {{\nu }_{V}}(s))}}{\kern 1pt} \frac{{{{B}_{V}}(s)x{{{(1 - x)}}^{{{{\nu }_{V}}(s) + 1}}}}}{{\left[ {\ln (1{\text{/}}(1 - x)) + \hat {c} + \Psi ({{\nu }_{V}}(s) + 2)} \right]}}, \\ \end{gathered} $$

(10)

$$f_{g}^{ + }(x,{{Q}^{2}}) = \left( {{{A}_{g}} + \frac{4}{9}{{A}_{q}}} \right){{I}_{0}}(\sigma ){{e}^{{ - {{{\overline d }}_{ + }}s}}}{{(1 - x)}^{{{{m}_{{g, + }}} + {{\nu }_{ + }}(s)}}}.$$

(11)

Here, Ψ is the Riemann’s Ψ-function and

$${{\nu }_{ \pm }}(s) = {{\nu }_{ \pm }}(0) + {{r}_{ \pm }}s,\quad {{B}_{ \pm }}(s) = {{B}_{ \pm }}(0){{e}^{{ - {{p}_{ \pm }}s}}},$$

$${{p}_{ \pm }} = {{r}_{ \pm }}({{\gamma }_{{\text{E}}}} + {{\hat {c}}_{ \pm }}),\quad {{r}_{ + }} = \frac{{12}}{{{{\beta }_{0}}}},\quad {{r}_{ - }} = \frac{{16}}{{3{{\beta }_{0}}}},$$

$${{\hat {c}}_{ + }} = - \frac{{{{\beta }_{0}}}}{{12}},\quad {{\hat {c}}_{ - }} = - \frac{3}{4},\quad {{K}_{ + }} = \frac{{3{{N}_{f}}}}{{10}},\quad {{K}_{ - }} = \frac{2}{5}.$$

(12)

Here, ${{I}_{0}}$ and ${{I}_{1}}$ are the modified Bessel functions with

$$\sigma = 2\sqrt {\left| {{{{\hat {d}}}_{ + }}} \right|s{\text{ln}}\left( {\frac{1}{x}} \right)} ,\quad \rho = \frac{\sigma }{{2\ln (1{\text{/}}x)}},\quad {{\hat {d}}_{ + }} = - \frac{{12}}{{{{\beta }_{0}}}},$$

$${{\overline d }_{ + }} = 1 + \frac{{20{{N}_{f}}}}{{27{{\beta }_{0}}}},\quad {{d}_{ - }} = \frac{{16{{N}_{f}}}}{{27{{\beta }_{0}}}}.$$

(13)

The factors ${{A}_{g}}$, ${{A}_{q}}$, ${{B}_{ \pm }}(0)$, and ${{\nu }_{ \pm }}(0)$ are taken to describe the HERA data on proton SF ${{F}_{2}}(x,{{Q}^{2}})$. The Q²-dependence of the subasymptotic terms $\sim {\kern 1pt} {{D}_{ \pm }}(s)$ is taken from the momentum conservation law. Following [26], we set ${{m}_{{q, - }}} = {{m}_{{g, + }}} = 2$ and ${{m}_{{q, + }}} = {{m}_{{g, - }}} = 1$. In this case, the small x asymptotics are suppressed at large x compared to the subasymptotic terms $\sim {\kern 1pt} {{D}_{ \pm }}(s)$. Moreover, the small x asymptotics contain the same powers of $(1 - x)$ factor for quarks and gluons.

3 RESCALING MODEL AT LARGE AND LOW $x$

According to the rescaling model [15–17], the DIS structure function $F_{2}^{p}(x,{{Q}^{2}})$ and, consequently, the valence and nonsinget parts of quark densities in the case of a nucleus A are modified at intermediate and large x as follows⁵

$$f_{i}^{A}(x,{{Q}^{2}}) = {{f}_{i}}(x,Q_{{A,V}}^{2}),$$

(14)

where $i = V$ or $NS$ and new scale $Q_{{A,V}}^{2}$ is related to Q² by [22]

$$s_{V}^{A}\, \equiv \,\ln \left( {\frac{{\ln (Q_{{A,V}}^{2}{\text{/}}\Lambda _{{{\text{QCD}}}}^{2})}}{{\ln (Q_{0}^{2}{\text{/}}\Lambda _{{{\text{QCD}}}}^{{\text{2}}})}}} \right)\, = \,s + \ln (1 + \delta _{V}^{A})\, \approx \,s + \delta _{V}^{A},$$

(15)

so the kernel modification of main variable s depends on the Q²-independent parameter $\delta _{V}^{A}$ having small values (see [22]). Then, the small x PDF asymptotics have been applied [22] to the small x region of the EMC effect using the simple fact that the rise of sea quark and gluons densities increases with increasing Q². Thus, in the case of nuclei, the PDF evolution scale is less than Q² and this can directly reproduce the shadowing effect observed in global fits. Since there are two components for each parton density, + and – ones, we have two free parameters $Q_{{A, \pm }}^{2}$ that can be determined from the analysis of experimental data for the EMC effect at low x values. Usually, it is convenient to study the following ratio

$$R_{i}^{{AD}}(x,{{Q}^{2}}) = \frac{{f_{i}^{A}(x,{{Q}^{2}})}}{{f_{i}^{D}(x,{{Q}^{2}})}},$$

(16)

where $i = S$, SI, or g. Taking advantage of the fact that the nuclear effect in the deuteron is very small, $f_{i}^{D}(x,{{Q}^{2}}) \approx {{f}_{i}}(x,{{Q}^{2}})$, we can assume⁶ that

$$\begin{gathered} F_{2}^{A}(x,{{Q}^{2}}) = \frac{5}{{18}}{\kern 1pt} f_{{SI}}^{A}(x,{{Q}^{2}}) + \frac{1}{6}{\kern 1pt} f_{{NS}}^{A}(x,{{Q}^{2}}), \\ f_{{SI}}^{A}(x,{{Q}^{2}}) = f_{S}^{A}(x,{{Q}^{2}}) + f_{V}^{A}(x,{{Q}^{2}}), \\ \end{gathered} $$

(17)

where $f_{V}^{A}(x,{{Q}^{2}})$ and $f_{{NS}}^{A}(x,{{Q}^{2}})$ are given by (14). The gluon and sea quark densities are calculated as combinations of ± components:

$$\begin{gathered} f_{a}^{{A, + }}(x,{{Q}^{2}}) = f_{a}^{{A, + }}(x,{{Q}^{2}}) + f_{a}^{{A, - }}(x,{{Q}^{2}}), \\ f_{a}^{{A, \pm }}(x,{{Q}^{2}}) = f_{a}^{ \pm }(x,Q_{{AD, \pm }}^{2}) \\ \end{gathered} $$

(18)

with a = g or S. The expressions for $f_{a}^{ \pm }(x,{{Q}^{2}})$ are given by (8)–(11) and corresponding values of $s_{ \pm }^{{AD}}$ turned out to be

$$s_{ \pm }^{{AD}} \equiv \ln \left( {\frac{{\ln (Q_{{AD, \pm }}^{2}{\text{/}}\Lambda _{{{\text{QCD}}}}^{2})}}{{\ln (Q_{0}^{2}{\text{/}}\Lambda _{{{\text{QCD}}}}^{{\text{2}}})}}} \right) = s + \ln (1 + \delta _{ \pm }^{{AD}}),$$

(19)

where $\delta _{ \pm }^{{AD}}$ can be obtained by fitting the NMC experimental data on structure function ratios $F_{2}^{A}(x,{{Q}^{2}}){\text{/}}F_{2}^{D}(x,{{Q}^{2}})$ [33].

4 NUMERICAL RESULTS

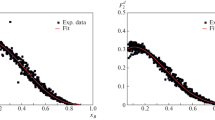
Performing fits on the NMC data [33] at low and moderate x values, $x \leqslant 0.7$, we obtained the values of $\delta _{ \pm }^{{AD}}$ for several nuclei targets. Our results are shown in Fig. 1 and collected in Table 1, where we additionaly show the $\delta _{V}^{{AD}}$ values taken from [22]. The goodness of our fit, ${{\chi }^{2}}{\text{/n}}{\text{.d}}{\text{.f}}.$, is presented also. One can see that newly fitted $\delta _{ + }^{{AD}}$ are about two times less than obtained earlier [22]. Moreover, we find that derived values of $\delta _{ - }^{{AD}}$ differ in sign from the previous results [22]. The main sourse of this difference is that the small-x PDF asymptotics have been used in the analysis [22] and, therefore, the NMC data were considered at low x only. In contrast, here we extended the consideration into the region of moderate x and take into account all NMC data points. Neverveless, strong difference in fitted $\delta _{ \pm }^{{AD}}$ leads to not so different results for nuclear modification factor $R$ at low $x$ values. It is because ${{Q}^{2}}$‑changes in the + and – components occur in opposite directions: in fact, the + (–) component increases (decreases) with by increasing Q². So, for the values of $\delta _{ \pm }^{{AD}}$ derived in previous analysis [22], the contribution of the – components is the opposite of the contribution of the + components. For the values of $\delta _{ \pm }^{{AD}}$ collected in Table 1, the contributions of the two components reinforce each other.

Fig. 1.

(Color online) The fit results of structure function ratios $F_{2}^{A}(x,{{Q}^{2}}){\text{/}}F_{2}^{D}(x,{{Q}^{2}})$ for several nuclear targets compared to the NMC experimental data [33].

Table 1. The $\delta _{ \pm }^{{AD}}$ parameters extracted from the NMC data [33] on structure function ratios $F_{2}^{A}(x,{{Q}^{2}}){\text{/}}F_{2}^{D}(x,{{Q}^{2}})$. The $\delta _{V}^{{AD}}$ values are taken from [22]

Since at low x the + component increases strongly with Q² growth, it is mainly responsable for the shadowing effect. For antishadowing, the contribution of the – component is more important. Strictly speaking, from momentum conservation in the case of a nuclear target⁷ one obtain $\delta _{ - }^{{AD}} = \delta _{V}^{{AD}}$. However, we cannot use momentum conservation here since we do not consider the large $x$ range, $x \geqslant 0.7$, where the Fermi motion should be taken into account.

Next, using the analytical expressions (5)–(13) for nucleon target, (14)–(19) for nuclear targets and fitted values of $\delta _{ \pm }^{{AD}}$, we can give predictions for nuclear modification factors $R_{i}^{{AD}}(x,{{Q}^{2}})$ defined by (16). Our results are shown in Fig. 2 for several nuclear targets, namely, ⁴He, ¹²C, and ⁴⁰Ca. Since, as is well known, $R_{i}^{{AD}}(x,{{Q}^{2}})$ are practically independent on Q², except may be low $x$ range, where, however, Q²-dependence is not so large, too. To save space, we show the results for ${{Q}^{2}} = 10$ GeV² only. We find that the shadowing effect for gluons is less than for quarks, that is consistent with the results of other studies [52, 53, 55–59]. Shadowing for antiquarks and quarks (sea and singlet quark densities, respectively) is very similar for $x \sim {{10}^{{ - 3}}}$, but a bit stronger for antiquarks at $x \sim {{10}^{{ - 3}}}$, that is in full agreement with predictions [52]. Gluon antishadowing is absent, which is also consistent with [52], where that antishadowing effect is very small. However, it is in disagreement with predictions of other groups [53, 55–57], where antishadowing has a great effect on gluons. The antishadowing for antiquarks is greater than for valence quarks, that contradicts the results of the study [52]. Other groups present results for antiquark antishadowing with large uncertainties, and therefore, it is difficult to draw any specific conclusion at present.

Fig. 2.

(Color online) The predicted nuclear modification factors for parton distributions in several nuclear targets. Fixed value ${{Q}^{2}} = 10$ GeV² is applied.

5 CONCLUSIONS

In the framework of rescaling model, we fitted the NMC experimental data for the ratios of the DIS structure functions ${{F}_{2}}(x,{{Q}^{2}})$ in nuclear targets and deuteron at low and intermediate x values, $x \leqslant 0.7$. Our analysis is based on the analytical expressions for proton PDFs derived previously in [26]. Using the obtained results for rescaling values, we derive predictions for nPDFs for several nuclear targets and, thus, for shadowing and antishadowing effects. We find that shadowing effect for gluons is less than for quarks, which is consistent with many other studies. There is no antishadowing for gluons, and it is better pronounced for antiquarks than for quarks. This is a rather interesting result, since different groups give very different results on the antishadowing effect with large uncertainties.

As the next steps, we plan to include the Fermi motion in our consideration and derive results for nuclear modifications of parton densities over the entire x range. Moreover, we plan to study nuclear modifications of Transverse Momentum Dependent parton distribution functions [60–63], which are now become very popular (see [64]) in the phenomenological analyses.