Does a Form Factor in Smith–Purcell Radiation Exist Always?

In the theory of radiation emitted by bunches of charged particles, the effects of coherence are commonly taken into account by multiplying the intensity of radiation generated by a single particle by the form factor of the bunch, which depends on its size, shape, and particle distribution. Here, it is demonstrated that this approach is, generally speaking, incorrect for polarization radiation from a wide class of structures like photonic crystals and metasurfaces. The theory of coherent Smith–Purcell radiation from such structures has been developed. It is shown that the commonly accepted approach is applicable only under two conditions: (i) the observation point lies in the plane containing the trajectory of the bunch and the normal to the surface of the target, and (ii) the radius of the bunch is much smaller than the effective range of the Coulomb field of the moving electrons.

1 INTRODUCTION

The coherence of radiation emitted by beams of charged particles is the main difference of synchrotrons of the third and, especially, the fourth generations from earlier ones and is a key phenomenon in the physics of free electron lasers, which are the brightest radiation sources ever built. Furthermore, it is the coherence of emitted radiation that underlies the diagnostics of the size of electron bunches in modern accelerators and colliders. Indeed, any experiments aimed at detecting transition radiation [1], diffraction radiation, including the better-known special case of Smith–Purcell radiation (SPR), or Cherenkov radiation [2–4] involve bunches of charged particles, and in order to compare the measured curves with the calculated ones, it is necessary to take into account the effect of both the bunch size and shape on the angular and frequency distributions of the intensity. In addition, coherence effects are also important in the existing sources of electromagnetic radiation relying on the SPR mechanism (e.g., the orotron [5]).

The generally accepted theoretical approach taking into account the coherence effects involves calculating the angular and frequency distributions of the intensity for a single electron and then multiplying the single-particle intensity by the form factor of the bunch. The latter is the sum of two terms, coherent and incoherent [6], and contains all information about the shape and size of the bunch. Usually, the incoherent term is assumed to be equal to the number of electrons in the bunch, and the coherent term is equal to the square of the number of electrons multiplied by the squared absolute value of the Fourier transform of the electron distribution function in the bunch. It was shown in [6] that, for edge types of radiation, such as Smith–Purcell, diffraction Cherenkov, or diffraction radiation, the coherent and incoherent terms in the form factor are different. In particular, it was shown that the incoherent form factor also contains information about the transverse dimensions of the bunch, and the coherent term is not simply the Fourier transform of the distribution function. It is essential that, as we pointed out in [6], these conclusions are valid for targets homogeneous along the surface in the direction transverse to the motion of the electron bunch.

Here, we demonstrate that, if the target is inhomogeneous in the direction perpendicular to the motion of the electron bunch, the concept of multiplying the single-particle intensity by the form factor to obtain the total intensity of Smith–Purcell or diffraction radiation is not always valid. To analyze the limits of its applicability, we calculate the SPR field produced by an electron bunch moving over a target periodic in the directions both parallel and perpendicular to the velocity of the bunch. Targets of this kind (metasurfaces, photonic crystals) have become the subject of intensive research today because of the possibilities to tailor the optical properties of the surface by controlling the spectrum of plasmon resonances and Smith–Purcell radiation or by designing micro- and nanoantennas [7], to develop new types of optical modulators [8] and filters [9], etc. In the physics of the emission of radiation by free electrons, structures of this type also attract a lot of attention [10–12], in terms of diagnostics of relativistic electron beams as well as of developing new radiation sources.

2 CONVENTIONAL APPROACH

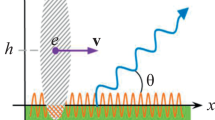
Smith–Purcell radiation is excited when charged particles travel near a target that is periodic in the direction of charge motion. Smith–Purcell radiation was experimentally observed in 1953 [13] and later studied in detail theoretically and experimentally for diffraction gratings of various profiles made from different materials [14–16]. If the inhomogeneity along the beam motion is arbitrary or aperiodic, the term diffraction radiation is used.

Coherence effects caused by the presence of many electrons in the bunch are frequently taken into account in the following manner. The intensity of radiation from one electron ${{I}_{1}}$ is calculated and is then multiplied by the form factor $F$ of the bunch. The form factor is taken in the form [1]

$$F = {{N}_{e}} + {{N}_{e}}({{N}_{e}} - 1){{F}_{{{\text{coh}}}}},$$

(1)

where ${{N}_{e}}$ is the number of electrons in the bunch and ${{F}_{{{\text{coh}}}}}$ is the squared absolute value of the Fourier transform of the electron distribution function $f({{{\mathbf{r}}}_{e}})$ in the bunch:

$${{F}_{{{\text{coh}}}}} = {{\left| {\int {{d}^{3}}{{r}_{e}}\exp ( - i\mathbf{k}{{\mathbf{r}}_{e}})f({{\mathbf{r}}_{e}})} \right|}^{2}};$$

(2)

here, k is the wave vector of radiation. This expression for the form factor is suitable for the case of synchrotron radiation, including radiation emitted at individual magnets and in undulators, or for radiation from targets whose size is effectively infinite in the direction transverse to the bunch motion (along the $OY$ axis). Integration in Eq. (2) is carried out with respect to the position vector r_e of the electron relative to the center of the bunch.

For diffraction or Smith–Purcell radiation, the form factor is written as [6]

$$F = {{N}_{e}}{{F}_{{{\text{inc}}}}} + {{N}_{e}}({{N}_{e}} - 1){{F}_{{{\text{coh}}}}},$$

(3)

where

$${{F}_{{{\text{inc}}}}} = \int {{d}^{3}}{{r}_{e}}{\text{|}}\exp ( - i\mathbf{q}{{\mathbf{r}}_{e}}){{{\text{|}}}^{2}}f({{\mathbf{r}}_{e}}),$$

(4)

$${{F}_{{{\text{coh}}}}} = {{\left| {\int {{d}^{3}}{{r}_{e}}\exp ( - i\mathbf{q}{{\mathbf{r}}_{e}})f({{\mathbf{r}}_{e}})} \right|}^{2}},$$

(5)

and $\mathbf{q} = ({{\beta }^{{ - 1}}},{{n}_{y}}, - i{{\gamma }^{{ - 1}}}{{\beta }^{{ - 1}}}\sqrt {1 + {{\gamma }^{2}}{{\beta }^{2}}n_{y}^{2}} )\omega {\text{/}}c$. Here, $c$ is the speed of light in free space, ω is the radiation frequency, $\beta = v{\text{/}}c$, $v$ is the velocity of electrons in the bunch, $\gamma = 1{\text{/}}\sqrt {1 - {{\beta }^{2}}}$ is the Lorentz factor of electrons, and ${{n}_{y}}$ is the y component of the unit vector along the direction of emission.

It was shown in [6] that the difference between Eqs. (1) and (3) is related to the spread in the distances from electrons to the target (see Fig. 1). The field produced by an individual electron decreases with this distance, so electrons located at different distances from the target contribute differently to its polarization. In short, we can say that the difference is caused by the spread in impact parameters. The impact parameter is the shortest distance between the electron trajectory and the target (see ${{h}_{1}}$ and ${{h}_{2}}$ in Fig. 1).

Fig. 1.

(Color online) Generation of diffraction or Smith–Purcell radiation. An electron bunch travels along the $OX$ axis at a constant velocity v. The electrons ${{e}_{1}}$ and ${{e}_{2}}$ in the bunch are located at different distances ${{h}_{1}}$ and ${{h}_{2}}$ from the target and make different contributions to the polarization of the target by their field.

As an example, let us consider a doubly periodic target such as a two-dimensional (2D) photonic crystal. Such targets are also often called metasurfaces. Strictly speaking, the prefix “meta” should mean that the wavelength significantly exceeds the dimensions of individual elements and, moreover, the spacing between them [17]. Today, however, this condition is omitted, especially in the Western literature. Then, metasurface means any artificially assembled two-dimensional structure with the possibility of designing the required optical properties. For the sake of rigor, we nevertheless will stick here to the term 2D photonic crystal (or photonic crystal slab). We will consider only 2D crystals in order to avoid the question of the influence of band gaps in the crystal on the characteristics of SPR (this issue was analyzed numerically in a series of papers by Ohtaka et al. [18–22]).

Figure 2 shows the scheme of SPR excitation when an electron bunch (blue arrow) travels over the surface of a 2D photonic crystal. The surface represents an ordered array of subwavelength particles, i.e., particles whose characteristic size L is much smaller than the radiation wavelength λ. The particles are located in a plane parallel to the electron trajectory. Let us choose the coordinate system where OX and OY axes lie in this plane, the origin is at the center of the target, and the bunch moves along the $OX$ axis at a constant velocity. The particles are arranged periodically in two directions: along the trajectory of the bunch with a period of ${{d}_{x}}$ and perpendicular to the trajectory with a period of ${{d}_{y}}$. The total number of particles is N.

Fig. 2.

(Color online) Coordinate system and scheme of excitation of Smith–Purcell radiation by an electron bunch traveling above a metasurface.

The position vectors of particles in the target sketched in Fig. 2 can be written as

$${\mathbf{R}_{m}} = {{d}_{x}}{{m}_{x}}{\mathbf{e}_{x}} + {{d}_{y}}{{m}_{y}}{\mathbf{e}_{y}} \equiv {{X}_{m}}{\mathbf{e}_{x}} + {{Y}_{m}}{\mathbf{e}_{y}},$$

(6)

where the indices ${{m}_{x}}$ and ${{m}_{y}}$ are integers enumerating particles in the target along the $OX$ and $OY$ axes, respectively. For example, the particle positions can be specified so that ${{m}_{x}}$ and ${{m}_{y}}$ vary between $- ({{N}_{{x,y}}} - 1){\text{/}}2$ and $({{N}_{{x,y}}} - 1){\text{/}}2$. Then, there are ${{N}_{x}}$ and ${{N}_{y}}$ lattice elements along the $OX$ and $OY$ axes, respectively, and the total number of elements is $N = {{N}_{x}}{{N}_{y}}$.

The velocity vector in the chosen coordinate system is v = ($v$, 0, 0). For ultrarelativistic electron bunches, the spread in the electron velocities and energies can be disregarded in the first approximation. This means that all electrons will be described by the same velocity vector. The center of the moving bunch remains at a constant distance h from the plane of the target.

For the considered geometry, the expression for the spectral and angular distribution of radiation from a single electron ${{I}_{1}}$ was obtained in [23]. Let us multiply this expression by the form factor and, for convenience, write out the resulting formula for the spectral and angular distribution of radiation from the bunch:

$$I = {{I}_{{{\text{inc}}}}} + {{I}_{{{\text{coh}}}}},$$

(7)

where

$${{I}_{{{\text{inc}}}}} = \frac{{{{e}^{2}}{{\omega }^{2}}{\text{|}}\alpha (\omega ){{{\text{|}}}^{2}}}}{{{{\pi }^{2}}{{c}^{3}}{{\beta }^{4}}{{\gamma }^{2}}}}S{{k}^{4}}{{N}_{e}}\iint d{{y}_{e}}d{{z}_{e}}$$

$$ \times \;{{e}^{{ - 2\frac{{\omega {{z}_{e}}}}{{\gamma v}}\sqrt {1 + {{\gamma }^{2}}{{\beta }^{2}}n_{y}^{2}} }}}{{f}_{{{\text{tr}}}}}({{y}_{e}},{{z}_{e}})$$

(8)

$$ \times \;\left\{ {{{{\left| {\sum\limits_{{{m}_{y}}} {{e}^{{ - i{{d}_{y}}{{m}_{y}}{{k}_{y}}}}}{\mathbf{P}_{m}}} \right|}}^{2}} - {{{\left| {\sum\limits_{{{m}_{y}}} {{e}^{{ - i{{d}_{y}}{{m}_{y}}{{k}_{y}}}}}\frac{{\mathbf{k}{\mathbf{P}_{m}}}}{k}} \right|}}^{2}}} \right\},$$

$${{I}_{{{\text{coh}}}}} = \frac{{{{e}^{2}}{{\omega }^{2}}{\text{|}}\alpha (\omega ){{{\text{|}}}^{2}}}}{{{{\pi }^{2}}{{c}^{3}}{{\beta }^{4}}{{\gamma }^{2}}}}{{k}^{4}}$$

$$\begin{gathered} \times \;{{\left| {\iint d{{y}_{e}}dz_{e}^{{ - i{{k}_{y}}{{y}_{e}} - {{z}_{e}}\frac{\omega }{{\gamma v}}\sqrt {1 + {{\gamma }^{2}}{{\beta }^{2}}n_{y}^{2}} }}{{f}_{{{\text{tr}}}}}({{y}_{e}},{{z}_{e}})} \right|}^{2}} \\ \times \;{{N}_{e}}({{N}_{e}} - 1)S{{F}_{l}} \\ \end{gathered} $$

(9)

$$ \times \;\left\{ {{{{\left| {\sum\limits_{{{m}_{y}}} {{e}^{{ - i{{d}_{y}}{{m}_{y}}{{k}_{y}}}}}{\mathbf{P}_{m}}} \right|}}^{2}} - {{{\left| {\sum\limits_{{{m}_{y}}} {{e}^{{ - i{{d}_{y}}{{m}_{y}}{{k}_{y}}}}}\frac{{\mathbf{k}{\mathbf{P}_{m}}}}{k}} \right|}}^{2}}} \right\}.$$

Deriving these expressions, we disregarded correlations between electrons and represented the electron distribution function in the bunch as the product of two factors f_l(x_e) and f_tr(y_e, z_e) describing the distributions in the longitudinal direction (along the $OX$ axis) and transverse direction, respectively:

$$f({{{\mathbf{r}}}_{e}}) = {{f}_{l}}({{x}_{e}}){{f}_{{{\text{tr}}}}}({{y}_{e}},{\text{ }}{{z}_{e}}).$$

(10)

This made it possible to obtain the longitudinal form factor as a separate coefficient

$${{F}_{l}} = {{\left| {\int d{{x}_{e}}{{f}_{l}}({{x}_{e}})\exp \left( { - i\omega \frac{{{{x}_{e}}}}{v}} \right)} \right|}^{2}}.$$

(11)

The functions f(r_e),  f_l(x_e), and  f_tr(y_e, z_e) are normalized to unity. The longitudinal form factor given by Eq. (11) enters only the term describing the coherent part of radiation.

In the above expressions, e is the elementary charge, $\alpha (\omega )$ is the polarizability of the particles composing the target, k is the length of the wave vector of radiation, and

$${\mathbf{P}_{m}} = \frac{\mathbf{v}}{{v\gamma }}{{K}_{0}}\left( {\frac{\omega }{{v\gamma }}{{\rho }_{m}}} \right) + i\frac{{{\boldsymbol{\rho }_{m}}}}{{{{\rho }_{m}}}}{{K}_{1}}\left( {\frac{\omega }{{v\gamma }}{{\rho }_{m}}} \right),$$

(12)

$${\boldsymbol{\rho }_{m}} = {{Y}_{m}}{\mathbf{e}_{y}} - h{\mathbf{e}_{z}}.$$

(13)

Here, ${{K}_{0}}$ and ${{K}_{1}}$ are the modified Bessel functions of the second kind of the zeroth and first order, respectively. Note that the vectors P_m and ρ_m are independent of the integration variable r_e, i.e., of the electron position in the bunch. Summation over the index ${{m}_{x}}$ results, after a number of manipulations, in the appearance of the factor

$$S = \frac{{\mathop {\sin }\nolimits^2 ({{d}_{x}}{{N}_{x}}({{k}_{x}} - \omega {\text{/}}v){\text{/}}2)}}{{\mathop {\sin }\nolimits^2 ({{d}_{x}}({{k}_{x}} - \omega {\text{/}}v){\text{/}}2)}}.$$

(14)

This factor is typical of SPR and determines the general shape of the spectral and angular distribution of radiation. The condition that S is maximal yields the dispersion relation

$$\lambda s = {{d}_{x}}({{\beta }^{{ - 1}}} - {{n}_{x}}),$$

(15)

where s is a positive integer. Expression (15) coincides with the classical dispersion relation for SPR from a conventional diffraction grating [13].

3 CONSISTENT APPROACH

Let us find the spectral–angular density of emitted radiation in a consistent way; i.e., we calculate the radiation fields generated by each of the electrons and average the intensity over the positions of all electrons in the bunch. The scheme of SPR excitation and the target design are the same as above (see Fig. 2).

The single-particle theory of SPR from the structures under consideration was described in detail in our works [23, 24]. To calculate the characteristics of radiation emitted by the bunch, it is necessary to calculate in much the same way the radiation fields for each electron and then average their superposition over the positions of electrons. Despite the similarity of the expressions with the single-particle theory, for the sake of presentation completeness, we briefly present here the scheme for calculating the radiation field for ${{N}_{e}}$ electrons.

The current density corresponding to a single electron initially located at a point with coordinates r_e + he_z = (x_e, y_e, z_e + h) can be written as

$$\mathbf{j}_{e}^{0}(\mathbf{r},t) = e\mathbf{v}\delta (\mathbf{r} - \mathbf{v}t - {\mathbf{r}_{e}} - h{\mathbf{e}_{z}}),$$

(16)

where δ is the delta function. The field created by the moving electron itself is determined by this current density, and its Fourier transform can be written as

$$\begin{gathered} \mathbf{E}_{e}^{0}(\mathbf{r},\omega ) = - \frac{{ie\omega }}{{\pi {{v}^{2}}\gamma }}\exp \left[ {i\omega \frac{{x - {{x}_{e}}}}{v}} \right] \\ \times \;\left\{ {\frac{\mathbf{v}}{{v\gamma }}{{K}_{0}}\left( {\frac{{\omega {{\rho }_{e}}}}{{v\gamma }}} \right) + i\frac{{{\boldsymbol{\rho }_{e}}}}{{{{\rho }_{e}}}}{{K}_{1}}\left( {\frac{{\omega {{\rho }_{e}}}}{{v\gamma }}} \right)} \right\}, \\ \end{gathered} $$

(17)

where

$${{{\boldsymbol{\rho }}}_{e}} = (y-{{y}_{e}}){{{\mathbf{e}}}_{y}} + (z-{{z}_{e}}-h){{{\mathbf{e}}}_{z}}.$$

(18)

This field induces dynamic polarization in the particles of the target, which leads to the emission of radiation. Since the particles are small compared to the radiation wavelength and interaction between the particles is negligible, the induced current density in the particles can be written as

$$\mathbf{j}(\mathbf{r},t) = \sum\limits_m \frac{\partial }{{\partial t}}\mathbf{d}({{\mathbf{R}}_{m}},t)\delta (\mathbf{r} - {\mathbf{R}_{m}}).$$

(19)

Here, summation is performed over all particles in the target, R_m is the position vector of the $m$th particle, and d(R_m, t) is the dipole moment at the point R_m, whose Fourier transform is determined by the expression

$$\mathbf{d}(\mathbf{r},\omega ) = \alpha (\omega )\sum\limits_e \mathbf{E}_{e}^{0}(\mathbf{r},\omega ),$$

(20)

where summation is carried out over all electrons in the bunch, and particle polarizability $\alpha (\omega )$ characterizes the response of an individual particle to external field (for simplicity, we assume that all particles in the target are identical, which does not limit the general character of our treatment).

The Fourier transform of the radiation field is the solution of Maxwell’s equations and is determined by the Fourier transform of the current density given by Eq. (19):

$${\mathbf{E}^{{{\text{rad}}}}}(\mathbf{q},\omega ) = - \frac{{4\pi i}}{\omega }\left( {\mathbf{j}(\mathbf{q},\omega ) + \frac{{[\mathbf{q},[\mathbf{q},\mathbf{j}(\mathbf{q},\omega )]]}}{{{{q}^{2}} - {{k}^{2}}}}} \right),$$

(21)

where $k = \omega {\text{/}}c$. At large distances, i.e., for $kr \gg 1$, the Fourier transform of the radiation field becomes

$${\mathbf{E}^{{{\text{rad}}}}}(\mathbf{r},\omega ) = - i\frac{{{{{(2\pi )}}^{3}}}}{\omega }\frac{{{{e}^{{ikr}}}}}{r}[\mathbf{k},[\mathbf{k},\mathbf{j}(\mathbf{k},\omega )]].$$

(22)

Ultimately, combining all of the above formulas, we obtain the following explicit expression for the radiation field emitted by an electron bunch traveling above a 2D-periodic target:

$$\begin{gathered} {\mathbf{E}^{{{\text{rad}}}}}(\mathbf{r},\omega ) = \frac{{ie\omega }}{{\pi {{v}^{2}}\gamma }}\alpha (\omega )\frac{{{{e}^{{ikr}}}}}{r} \\ \times \;\sum\limits_e {{e}^{{ - i\omega \frac{{{{x}_{e}}}}{v}}}}\sum\limits_m {{e}^{{i\left( {\omega \frac{\mathbf{v}}{{{{v}^{2}}}} - \mathbf{k}} \right){\mathbf{R}_{m}}}}}[\mathbf{k},[\mathbf{k},{\mathbf{P}_{{me}}}]], \\ \end{gathered} $$

(23)

where

$${\mathbf{P}_{{me}}} = \frac{\mathbf{v}}{{v\gamma }}{{K}_{0}}\left( {\frac{{\omega {{\rho }_{{me}}}}}{{v\gamma }}} \right) + i\frac{{{\boldsymbol{\rho }_{{me}}}}}{{{{\rho }_{{me}}}}}{{K}_{1}}\left( {\frac{{\omega {{\rho }_{{me}}}}}{{v\gamma }}} \right)$$

(24)

and

$${{{\boldsymbol{\rho }}}_{{me}}} = ({{Y}_{m}}-{{y}_{e}}){{{\mathbf{e}}}_{y}}-(h + {{z}_{e}}){{{\mathbf{e}}}_{z}}.$$

(25)

Therefore, the radiation field generated by the bunch depends on the relative vectors ρ_me of all electrons in the bunch with respect to all particles in the target. The vector ρ_me has the meaning of an effective impact parameter, i.e., the shortest distance between the trajectory of the eth electron and the mth element of the target (see Fig. 3).

Fig. 3.

(Color online) Geometrical meaning of the vector ρ_me as the effective impact parameter.

The spectral and angular distribution of the radiation energy at large distances is determined by the squared magnitude of the field given by Eq. (23), which can be written as

$$\begin{gathered} \frac{{{{d}^{2}}W(\mathbf{n},\omega )}}{{d\omega d\Omega }} = \frac{{{{e}^{2}}{{\omega }^{2}}c}}{{{{\pi }^{2}}{{v}^{4}}{{\gamma }^{2}}}}{\text{|}}\alpha (\omega ){{{\text{|}}}^{2}} \\ \times \;{{\left| {\sum\limits_e {{e}^{{ - i\omega \frac{{{{x}_{e}}}}{v}}}}\sum\limits_m {{e}^{{i\left( {\omega \frac{\mathbf{v}}{{{{v}^{2}}}} - \mathbf{k}} \right){\mathbf{R}_{m}}}}}[\mathbf{k},[\mathbf{k},{\mathbf{P}_{{me}}}]]} \right|}^{2}}. \\ \end{gathered} $$

(26)

Using the known properties of sums, let us split the squared absolute value of the sum over all electrons into two parts, comprising all diagonal and off-diagonal terms, respectively. Then, the spectral and angular distribution of the radiation energy will also be represented as the sum of the incoherent and coherent parts, which can be written as

$$\begin{gathered} \frac{{{{d}^{2}}{{W}_{{{\text{inc}}}}}(\mathbf{n},\omega )}}{{d\omega d\Omega }} = \frac{{{{e}^{2}}{{\omega }^{2}}c}}{{{{\pi }^{2}}{{v}^{4}}{{\gamma }^{2}}}}{\text{|}}\alpha (\omega ){{{\text{|}}}^{2}} \\ \times \;\sum\limits_e {{\left| {\sum\limits_m {{e}^{{i\left( {\omega \frac{\mathbf{v}}{{{{v}^{2}}}} - \mathbf{k}} \right){\mathbf{R}_{m}}}}}[\mathbf{k},[\mathbf{k},{\mathbf{P}_{{me}}}]]} \right|}^{2}} \\ \end{gathered} $$

(27)

and

$$\frac{{{{d}^{2}}{{W}_{{{\text{coh}}}}}(\mathbf{n},\omega )}}{{d\omega d\Omega }} = \frac{{{{e}^{2}}{{\omega }^{2}}c}}{{{{\pi }^{2}}{{v}^{4}}{{\gamma }^{2}}}}{\text{|}}\alpha (\omega {\text{)}}{{{\text{|}}}^{2}}$$

$$ \times \;\left( {\sum\limits_e {{e}^{{ - i\omega \frac{{{{x}_{e}}}}{v}}}}\sum\limits_m {{e}^{{i\left( {\omega \frac{\mathbf{v}}{{{{v}^{2}}}} - \mathbf{k}} \right){\mathbf{R}_{m}}}}}[\mathbf{k},[\mathbf{k},{\mathbf{P}_{{me}}}]]} \right)$$

(28)

$$ \times \;\left( {\sum\limits_{e' \ne e} {{e}^{{i\omega \frac{{{{x}_{e}}}}{v}}}}\sum\limits_m {{e}^{{ - i\left( {\omega \frac{\mathbf{v}}{{{{v}^{2}}}} - \mathbf{k}} \right){\mathbf{R}_{m}}}}}[\mathbf{k},[\mathbf{k},\mathbf{P}_{{me}}^{*}]]} \right),$$

respectively (here, the asterisk designates complex conjugation).

Next, we need to average Eqs. (27) and (28) with respect to the electron coordinates using the electron distribution function in the bunch f(r_e) as the weight function. Such averaging reduces to the integration of Eqs. (27) and (28) over r_e. Then, the spectral and angular distribution of radiation from the bunch takes the form

$$\left\langle {\frac{{{{d}^{2}}W(\mathbf{n},\omega )}}{{d\omega d\Omega }}} \right\rangle = \left\langle {\frac{{{{d}^{2}}{{W}_{{{\text{inc}}}}}(\mathbf{n},\omega )}}{{d\omega d\Omega }}} \right\rangle + \left\langle {\frac{{{{d}^{2}}{{W}_{{{\text{coh}}}}}(\mathbf{n},\omega )}}{{d\omega d\Omega }}} \right\rangle ,$$

(29)

where angle brackets designate averaging. In a shorter form,

$$I{\kern 1pt} ' = I_{{{\text{inc}}}}^{'} + I_{{{\text{coh}}}}^{'}.$$

(30)

The incoherent and coherent terms are given by the expressions

$$\begin{gathered} I_{{{\text{inc}}}}^{'} = \frac{{{{e}^{2}}{{\omega }^{2}}c}}{{{{\pi }^{2}}{{v}^{4}}{{\gamma }^{2}}}}{{k}^{4}}{\text{|}}\alpha (\omega ){{{\text{|}}}^{2}}S{{N}_{e}}\iint d{{y}_{e}}d{{z}_{e}}{{f}_{{tr}}} \\ \times \;\left\{ {{{{\left| {\sum\limits_{{{m}_{y}}} {{e}^{{ - i{{k}_{y}}{{d}_{y}}{{m}_{y}}}}}{\mathbf{P}_{{me}}}} \right|}}^{2}} - {{{\left| {\sum\limits_{{{m}_{y}}} {{e}^{{ - i{{k}_{y}}{{d}_{y}}{{m}_{y}}}}}\frac{{\mathbf{k}{\mathbf{P}_{{me}}}}}{k}} \right|}}^{2}}} \right\} \\ \end{gathered} $$

(31)

and

$$I_{{{\text{coh}}}}^{'} = \frac{{{{e}^{2}}{{\omega }^{2}}c}}{{{{\pi }^{2}}{{v}^{4}}{{\gamma }^{2}}}}{{k}^{4}}{\text{|}}\alpha (\omega ){{{\text{|}}}^{2}}S{{N}_{e}}({{N}_{e}} - 1){{F}_{l}}$$

$$ \times \;\left\{ {{{{\left| {\sum\limits_{{{m}_{y}}} {{e}^{{ - i{{k}_{y}}{{d}_{y}}{{m}_{y}}}}}\iint d{{y}_{e}}d{{z}_{e}}{{f}_{{tr}}}{\mathbf{P}_{{me}}}} \right|}}^{2}}} \right.$$

(32)

$$\left. { - \;{{{\left| {\sum\limits_{{{m}_{y}}} {{e}^{{ - i{{k}_{y}}{{d}_{y}}{{m}_{y}}}}}\iint d{{y}_{e}}d{{z}_{e}}{{f}_{{tr}}}\frac{{{\mathbf{k}}{\mathbf{P}_{{me}}}}}{k}} \right|}}^{2}}} \right\},$$

respectively. Here, ${{N}_{e}}$ in Eqs. (31) and (32) is the number of electrons in the bunch. As one would expect, the intensities of coherent and incoherent radiation are proportional to $N_{e}^{2}$ and ${{N}_{e}}$, respectively. According to the analysis of the general expressions (31) and (32), without specifying the shape of the bunch and the geometry of the target, contrary to the commonly held belief, incoherent radiation contains information about the size of the bunch, although only about the transverse size. At the same time, coherent radiation depends on both the transverse and longitudinal sizes of the bunch. Note that, in contrast to the approach discussed in the preceding section, the vectors P_me and ρ_me here depend on the electron position in the bunch, i.e., on the integration variable.

4 COMPARISON OF THE TWO APPROACHES

Let us find out when calculations using the two above approaches yield the same radiation intensities. Omitting identical factors, we see that Eqs. (8) and (9) coincide with Eqs. (31) and (32), respectively, if

$$\mathbf{P}({\boldsymbol{\rho }_{m}}){{e}^{{ - i{{k}_{y}}{{y}_{e}}}}}{{e}^{{ - {{z}_{e}}\frac{\omega }{{\gamma v}}\sqrt {1 + {{\gamma }^{2}}{{\beta }^{2}}n_{y}^{2}} }}} \approx \mathbf{P}({\boldsymbol{\rho }_{m}} - {\mathbf{r}_{{e \bot }}}),$$

(33)

where ${\mathbf{r}_{{e \bot }}} = {{y}_{e}}{\mathbf{e}_{y}} + {{z}_{e}}{\mathbf{e}_{z}}$. We note that the left-hand side of Eq. (33) depends on the observation angles, in contrast to the right-hand side.

The decreasing exponential factor in Eq. (33) is maximal for ${{n}_{y}} = 0$. By letting ${{n}_{y}} = 0$, we find that condition (33) can be split into two conditions:

$${{K}_{0}}\left( {\frac{\omega }{{v\gamma }}{{\rho }_{m}}} \right){{e}^{{ - {{z}_{e}}\frac{\omega }{{\gamma v}}}}} \approx {{K}_{0}}\left( {\frac{\omega }{{v\gamma }}{\text{|}}{\boldsymbol{\rho }_{m}} - {\mathbf{r}_{{e \bot }}}} \right),$$

(34)

and

$$\frac{{{\boldsymbol{\rho }_{m}}}}{{{{\rho }_{m}}}}{{K}_{1}}\left( {\frac{\omega }{{v\gamma }}{{\rho }_{m}}} \right){{e}^{{ - {{z}_{e}}\frac{\omega }{{\gamma v}}}}} \approx \frac{{{\boldsymbol{\rho }_{m}} - {\mathbf{r}_{{e \bot }}}}}{{{\text{|}}{\boldsymbol{\rho }_{m}} - {\mathbf{r}_{{e \bot }}}{\text{|}}}}{{K}_{1}}\left( {\frac{\omega }{{v\gamma }}{\text{|}}{\boldsymbol{\rho }_{m}} - {\mathbf{r}_{{e \bot }}}{\text{|}}} \right).$$

(35)

These conditions are satisfied when

$${{z}_{e}}\frac{\omega }{{\gamma v}} \ll 1,\quad {{r}_{{e \bot }}} \ll {{\rho }_{m}}.$$

(36)

These inequalities have to be valid for any value of ${{m}_{y}}$. The second of inequalities (36) can be replaced by a stricter one, where the largest value of ρ_m is substituted. Then, for a bunch with a radius of ${{r}_{0}}$, we obtain

$${{z}_{e}} \ll \frac{{\gamma \beta \lambda }}{{2\pi }},\quad {{r}_{0}} \ll \sqrt {{{{\left( {\frac{{{{L}_{y}}}}{2}} \right)}}^{2}} + {{h}^{2}}} .$$

(37)

Here, ${{L}_{y}} = {{d}_{y}}{{N}_{y}}$ is the width of the target. Obtaining a high efficiency of the SPR emission requires that the impact parameter be smaller than the effective range of the field of electrons, i.e., $h < \gamma \beta \lambda {\text{/}}(2\pi )$. Then, the two conditions of Eq. (37) can be replaced with the following one:

$${{r}_{0}} \ll \frac{{\gamma \beta \lambda }}{{2\pi }}.$$

(38)

Therefore, the common approach is valid only when radiation is observed in the plane containing the electron bunch path and the target normal and for the bunches whose transverse dimensions are much smaller than the effective radius $\gamma \beta \lambda {\text{/}}(2\pi )$ of the Co-ulomb field of electrons. The first condition does not significantly limit the generality, since the radiation intensity is highest in the plane ${{n}_{y}} = 0$ or is comparable with other directions. The second condition, which is quite restrictive, means physically that the size of the bunch should be so small that the contributions from all electrons to the polarization of the target are the same. Then, the contribution of the transverse dimensions of the bunch to the angular and frequency distributions of radiation in the given experiment is negligible. When condition (38) is met, the transverse form factors

$${{F}_{{{\text{coh}},{\kern 1pt} tr}}} = {{\left| {\iint d{{y}_{e}}d{{z}_{e}}\exp ( - i{\mathbf{qr}_{e}}){{f}_{{tr}}}} \right|}^{2}},$$

(39)

$${{F}_{{{\text{inc}},{\kern 1pt} tr}}} = \iint d{{y}_{e}}d{{z}_{e}}{{\left| {\exp ( - i{\mathbf{qr}_{e}})} \right|}^{2}}{{f}_{{tr}}}$$

(40)

hardly differ from unity (F_{coh, tr} ≈ F_{inc, tr} ≈ 1) [6]. We note that good agreement between the theoretical and experimental curves was demonstrated just under these conditions [25].

If such a target is used to characterize the transverse dimensions of a bunch or if the experimental conditions imply that the transverse dimensions contribute to the total intensity distributions, the approach of multiplying the single-particle distribution by the form factor is invalid.

5 CONCLUSIONS

To summarize, we have analyzed the possible approaches to taking into account coherence effects in Smith–Purcell radiation from ultrarelativistic electron bunches. The radiation field excited by such a bunch traveling above a 2D photonic crystal has been calculated. It has been shown by this example that the commonly accepted approach based on multiplying the intensity of radiation produced by a single electron by the form factor of the bunch can be applicable for targets inhomogeneous in the transverse direction only under two conditions: (i) the observation point lies in the plane containing the trajectory of the bunch and the normal to the target surface, and (ii) the radius of the bunch is much smaller than the effective radius $\gamma \beta \lambda /(2\pi )$ of the Coulomb field of moving electrons.

The first of these conditions is not critical, since the radiation intensity is the highest in this plane, and it is satisfied in most experiments. The second condition severely limits the applicability of the commonly accepted approach: it remains true only if the size of the bunch has no effect on the angular and frequency distributions of the intensity. If any of these two conditions are violated, then one needs to consistently calculate the radiation fields from each electron and then average the intensity with respect to the electron positions in the bunch. This calculation is outlined in S-ection 3.

The difference between the two approaches is explained by the occurrence of a spread in impact parameters even for a single electron: a given electron of the bunch is located at different distances from different elements of the target and so polarizes them differently, thus making different contributions to the angular and frequency distributions of the intensity.

The above conclusions are valid for diffraction or Smith–Purcell radiation from targets that are inhomogeneous in the direction perpendicular to the trajectory of the bunch; metasurfaces and photonic crystals, which are widely studied today, represent precisely this kind of target.