INTRODUCTION

Dispersed metallic powders are widely used in practice; thus, there is a large amount of research on the condensation of metal nanoparticles. Experimental studies of the size distribution functions of nanoparticles showed that the particle growth process differs from the classical atom attachment to a cluster [1, 2], and coagulation occurs at some condensation stages as a result of collisions of small particles [3]. For macroscopic simulations of coagulation, it is necessary to determine the frequency of collisions of clusters with each other. In addition to their speeds and concentrations, the values ​​of interaction cross sections should also be known.

The literature describes several methods to determine the cross section of cluster interaction. The simplest of them is based on the notion of a cluster as a clot of bulk fluid, an approximation of a “liquid drop” [4]. In this approximation, the radius \({{R}_{n}}\) of n atomic cluster is calculated by the formula

$${{R}_{n}} = {{\left( {\frac{{3{{m}_{1}}}}{{4\pi \rho }}} \right)}^{{1/3}}}{{n}^{{1/3}}},$$
((1))

where \({{m}_{1}}\) is the atomic weight and \(\rho \) is the liquid density. The section of interactions is further calculated on the basis of radii values as

$${{\sigma }_{{n,m}}} = \pi {{\left( {{{R}_{n}} + {{R}_{m}}} \right)}^{2}}.$$

The applicability of relation (1) to small clusters (n < 50) has not been evaluated, although it is well known that small clusters are loose and heterogeneous objects [5]; therefore, the use of (1) should result in a large error.

In the “hard sphere” method, cluster radii are expressed in terms of rotation radii, which are calculated from molecular dynamics (MD) simulation data as \({{R}_{{n,hs}}} = \sqrt {5{\text{/}}2} {{R}_{{n,{\text{gyr}}}}} + {{R}_{1}},\) here \({{R}_{{n{\text{,gyr}}}}}\) is the gyration radius averaged over the ensemble; \({{R}_{1}}\) is the equivalent atomic radius of 0.5d; and d is the interatomic distance at which the attraction between atoms is replaced by repulsion [6].

It was proposed that the cluster radius be determined through a point in the middle of the transition region between the dense core and the surrounding vapor [5]. This method cannot be applied to small clusters, as they do not have a dense core.

At present, the direct method to determine the interaction cross section according to MD modeling calculated by the molecular kinetic theory (MKT) is

$${{\sigma }_{{n,m}}} = \frac{{{{Z}_{{n,m}}}}}{{{{{v}}_{{n,m}}}{{C}_{n}}{{C}_{m}}}},$$
((2))

where \({{Z}_{{n,m}}}\) is the frequency of collisions between n and m atom clusters, \({{C}_{n}}{\text{ and }}{{C}_{m}}\) are the concentrations, and \({{{v}}_{{n,m}}}\) is the relative rate of heat motion of clusters [7].

The goal of the work is a statistical analysis of the MD simulation results of condensation of copper vapor to determine the radii of a small cluster on the basis of collision frequency.

SCHEME OF MOLECULAR DYNAMICS EXPERIMENT

Nanoparticle formation was studied by the method of molecular dynamics (MD), which was implemented in the LAMMPS software for multiprocessor calculations [8]. The system consisted of buffer gas atoms (Ar) and metal atoms (Cu). The interaction of copper atoms was described by the embedded atom potential [9]. The application of the potential [9] to the study of the Cu2 molecule gave a value of 2.44 eV for the dissociation energy and 2.14 Å for the molecular bond length. The experimental data are 2.01 ± 0.08 eV and 2.219 Å, respectively [10]. Thus, the errors are ~15% for energy and ~5% for the interatomic distance. The study suggests that the potential [9] adequately describes small copper clusters. The Ar–Ar and Cu–Ar interactions were described by the Lennard–Jones type potential with parameters e = 0.0123 eV, a = 3.76 Å. The potential cut-off radius was 10 Å. The time step in the system was 3 fs.

The atoms were placed in a cubic cell, and the periodic boundary conditions were set at the edges of the cell. The thermostat was used only for inert gas atoms. Calculations were carried out for argon temperatures \({{T}_{{{\text{Ar}}}}} = 30{\text{0 and 1500 K}}\) and copper vapor densities \({{\rho }_{{{\text{Cu}}}}}\)= 0.1–0.3 kg/m3. The ratio between the number of argon atoms and metal atoms was 3 : 1 with the number of metal atoms equal to 5000. These particle systems were considered for times on the order of 500 ns. Different initial configurations of atoms were calculated in order to collect a sufficient sample size for statistical analysis (at least 100 collisions per value \({{\sigma }_{{n,m}}}\)). Special initial configurations containing n atomic clusters and copper and argon atoms were created in order to obtain values ​​of frequencies \({{Z}_{{n,1}}},\)\({{Z}_{{n,2}}}\) and \({{Z}_{{n,3}}},\)n > 10 that were sufficient for analysis. To create them, one hundred n atomic clusters (n > 10) were randomly placed in a cell, the velocities of their centers of mass were distributed according to Maxwell’s law, and the coordinates and velocities of atoms in a cluster’s center of mass system were taken from the results of previous MD calculations. Additional copper and argon atoms were randomly located in the cell, and their velocities were distributed over Maxwell.

RESULTS AND DISCUSSION

Distance Selection Δ for Joint Path Analysis

The selection of a collision in the course of motion of atoms and clusters, which interact with each other through extended potentials, is not an easy problem. A collision between clusters is an event involving the convergence of atoms belonging to these clusters by a distance equal to or less than a certain Δ [11]. The Δ value is determined by the type of potential, but there is no strict quantitative criterion for the calculation of Δ. Meanwhile, the correct choice of Δ is very important, since the recorded number of collisions between clusters and, therefore, the calculated interaction cross section is directly dependent on the value of Δ. Here, it is necessary to take into account the fact that a large Δ value leads to an accounting for the cases of passage of atoms at a considerable distance from each other without a true collision. However, the chosen distance Δ cannot be too small, since the short-term separation of an atom from the cluster in this case will be considered cluster decay, and the subsequent approximation will be considered a new interaction, which will also lead to an unreasonable increase in the collision frequency.

It is convenient to formulate the selection criterion Δ on the example of the interaction of two atoms. A typical dimer, which is a result of the collision of atoms, is formed as follows: atoms begin to strongly attract each other and approach each other. In the approach, attraction is replaced by repulsion; atoms are inhibited and then can fly apart or form a long-lived dimer in which atoms rotate around the center of mass [12]. Thus, it is necessary to choose Δ such that a collision is considered to be a convergence of atoms at which the interaction would be observed as the repulsive part of the potential.

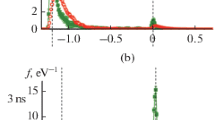
To formulate the criterion for the correct determination of Δ, we consider the distribution functions of copper dimers over the lifetime (Fig. 1) obtained for \(\Delta = 5\) Å (solid line) and \(\Delta = 4.95\) Å (dotted line). The dimer lifetime refers to the time interval during which the distance between the centers of mass of its atoms is equal to or less than \(\Delta .\) The lifetime distribution function of dimers \(f\left( \tau \right)\) is found over the interval \(0 < \tau < 1.5{\text{ ps}}\) with a sampling step of \(\delta \tau = 15{\text{ fs}}{\text{.}}\) The resulting function was normalized such that the area under the curve was equal to one. The time interval in which the statistics were collected amounted to 100 ns.

Fig. 1.
figure 1

Function of copper-dimer distributions by lifetimes at \({{T}_{{{\text{Ar}}}}} = 1500{\text{ K}}{\text{,}}\)\({{\rho }_{{{\text{Cu}}}}} = 0.25{\text{ kg }}{{{\text{m}}}^{{ - 3}}}{\text{:}}\) solid line—\(\Delta = 5\) Å, dotted line—\(4.95.\)

Full size image

The graph of the function constructed for \(\Delta = 5\) Å shows that for small values ​​of τ there is a prepeak or a plateau, whereas this feature is absent on the graph for \(\Delta = 4.95\) Å. The analysis shows that the plateau is formed by dimers, the atoms of which did not converge but flew past practically without deviation. If we gradually reduce Δ, then we can ensure that such dimers are not considered in the analysis. Based on this, the following rule was formulated for the selection of Δ: this is the highest distance at which atoms passing by each other without trajectory bending do not contribute to the collision statistics (there is no plateau for small τ in the distribution function). Calculations showed that, this distance can be taken as \(\Delta = 4.95\) Å for the potential of an immersed atom used to describe the interaction of copper atoms.

Determination of Cluster Radii

Analysis of the dependence of the cluster radius on the number of atoms in it was analyzed as follows. According to the data on the number of collisions between n atomic clusters and atoms, the cross section of the cluster–atom interaction \({{\sigma }_{{n,m}}}\) was calculated with formula (2) and m = 1 based on the values ​​of thermal translational velocity and concentration values. The relative cluster velocity was as \({{{v}}_{{n,m}}} = \sqrt {{\bar {v}}_{n}^{2} + {\bar {v}}_{m}^{2}} \) [7], where \({{{\bar {v}}}_{n}}\) and \({{{\bar {v}}}_{m}}\) are the average velocities of thermal translational motion of the center of the cluster mass, which was found via direct averaging over the ensemble. The “effective’ radius of the copper atom was calculated as \({{R}_{{\text{1}}}} = 0.5\sqrt {{{{{\sigma }_{{{\text{1}}{\text{.1}}}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{{\text{1}}{\text{.1}}}}}} \pi }} \right. \kern-0em} \pi }} \), and the cluster radii were further calculated with \(n > {\text{1}}\) as \({{R}_{n}} = \sqrt {{{{{\sigma }_{{n,1}}}} \mathord{\left/ {\vphantom {{{{\sigma }_{{n,1}}}} \pi }} \right. \kern-0em} \pi }} - {{R}_{1}}.\) The same algorithm was used to calculate cluster radii with cluster–dimer \({{\sigma }_{{n,2}}}\) and cluster–trimer \({{\sigma }_{{n,3}}}\) collision cross section data.

Figure 2 shows the dependences of cluster radii on the number of atoms in them. The symbols in Fig. 2 show the radii obtained from analysis of the frequency of cluster collisions with atoms, dimmers, and trimers. MD simulation was performed for 29 initial configurations with initial temperatures of 300 and 1500 K and copper vapor densities of 0.1–0.3 kg/m3. The time interval for counting the collision number was set at 10 ns. This value satisfies two conditions: the interval must be small so that its concentration and average velocities do not change significantly, and it must provide a collisions number large enough for statistical analysis. The time for considering the evolution of each configuration was ~500 ns, so it was possible to obtain several (the upper limit is 50) cross section values. The errors shown in the graph were obtained as a result of statistical processing of these data.

Fig. 2.
figure 2

Dependences of cluster radii versus the atomic number at \(\Delta = 4.95\) Å: (1) approximation \(R = 2.46{{(n - 0.052)}^{{0.31}}},\) (2) (1), (3) \({{T}_{{{\text{Ar}}}}}\) = 1500 K, (4) 300.

Full size image

Analysis of Fig. 2 makes it possible to conclude that the cluster radii under the considered conditions do not show a dependence on temperature or vapor density; the data is well approximated by the function

$${{R}_{n}} = 2.46{{n}^{{0.31}}},$$
((3))

where the exponent n is close to the classical cubic root. The graph obtained from analysis of the collision frequency lies much higher than the graph constructed for the “liquid drop.” Thus, the evaluation carried out according to (3) shows that the calculated average density of the copper cluster is 3.5 times lower than the density of liquid copper for n = 50. Since the used potential correctly describes the density of the solid phase [9] and equilibrium molecules, it can be concluded that such a low density is a property of small clusters during their growth. This is due to the fact that the state of matter in small clusters (n < 50) is similar to the gaseous state, in which atoms can move throughout the entire volume of cluster. Visualization of atomic motion in small clusters obtained in the process of condensation confirms this.

CONCLUSIONS

Thus, the “effective” radius of a cluster containing n atoms is satisfactorily described by the formula \({{R}_{n}} = 0.5\Delta {{n}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}.\)

The difference between the cluster radii obtained in this work and the results of the application formula (1) decreases (in percentage) with increasing n. Thus, the difference is ~40.5% from the cluster radius for \(n = {\text{2}}\) and decreases down to 34% for \(n = 45.\) The estimate for larger clusters shows a decrease in the relative difference, e.g., for n = 10 000, the difference value is ~25%. In other words, as n increases in the limit, the cluster density will probably approach the density of bulk liquid.