The Color of Solar Corona Structures

Abstract

Two-dimensional distributions of the relative color index (RCI) of the continuous corona spectrum of 1991 and 2006 reveal that the energy distributions in the continuums of the corona and photosphere differ, as do the RCI values for different coronal structures. The approximate symmetry of RCI distributions relative to the HCS projection on the sky plane excludes the contribution of the dust component. The revealed reddening with distance over the entire corona at all position angles is explained by the propagation of electron fluxes in the entire corona volume. It is noted that scattering by bound ion electrons causes bluing at distances of <1.3 R_☉. Thus, studies of coronal color give information about the dynamics of the electron component of the coronal plasma and the composition of the coronal matter.

1 INTRODUCTION

Until recently, the color of “white” coronal emission is studied only during total solar eclipses (TSEs). The term white corona refers to the coronal emission in the continuous spectrum of the visible and near IR ranges. It consists of two main components, K and F. The glow of the K corona, the electron component of the coronal plasma, is caused by Thomson scattering (scattering of low-frequency quanta of the electromagnetic radiation of the photosphere by the free resting electrons of the hot coronal plasma at T ~ 10⁶ K) and does not depend on the wavelength λ . The F corona is the dust component, which is physically not coupled to the corona. The mechanism of its glow is scattering of the photospheric radiation by dust particles surrounding the Sun.

The color of the coronal continuum is determined based on comparative analysis of the energy distribution of the coronal and photospheric continua via spectral or filter methods. If the distributions are identical, one can speak of a white color. A shift to the blue spectrum range indicates bluing, and a shift to the red spectrum range indicates reddening. I. Shklovsky (1965) presented a comprehensive survey on the determination of coronal color with use of filter and spectral methods in the first half of the 20th century. He pointed to the fact that scattering by free electrons and bound electrons (ions), as well as the composition of the coronal matter, can be studied via comparison of the continuous spectra of the corona and photosphere.

Later, to study the corona color, G.M. Nikol’skii initiated the use of quantitative color photographic photometry based on the use of color negative and positive films (Ajmanov and Nikolsky, 1980; Nikol’skii and Nesmyanovich, 1983). Reddening, which is sometimes found within the distance range of >1.2 R_☉ (the distances are counted from the Sun’s center), was attributed as a rule to the contribution of the F corona and interpreted with the presence of dust or dust rings at certain distances. It was also assumed that the energy distributions in the continuous spectra of the photosphere and K corona are identical. A series of works by Slovak and Czech astronomers on the search for bluing in the inner corona in TSE observations in 1994, 1995, 1997, and 1998 did not yield unambiguous results (see the short survey by Dorotovič and Rybanský (1997)). Surveys of works on the determination of the continuum color performed before the 2000s indicate inconsistency of the results.

It is known that K-coronal emission prevails in the distance range of <2 R_☉. Let us consider the possible use studies of corona color to study the K-corona dynamics. In 1976, Cram (1976) theoretically demonstrated the ability to obtain information about the electron velocity V_e and electron temperature T_e from spectral measurements of the ratio of intensities at 410 and 390 nm. Only 20 years later, Japanese researchers (Ichimoto et al., 1996), based on observations at 390 and 430 nm, and, later, American researchers (Reginald and Davila, 2000) verified this possibility experimentally from observations of spectra during TSEs. The disadvantages of spectral methods may include the obtainment of information that does not cover the entire corona but only the direction of the slit, as well as the effect of instrumental polarization of the spectrograph, which can considerably distort the results of the comparison of the continuous spectra of the corona and photosphere (Lipsky, 1958). In 2009, there appeared a unique (in our opinion) work by Reginald et al. (2009), in which it was shown theoretically for the first time that, in the presence of electron fluxes propagating from the Sun (solar wind), the shift of the K-coronal continuum to the red side over the entire corona must be registered for an observer on the Earth.

The goal of our work is to analyze, in contrast to previous research, the possible use of the determination of the coronal continuum color to study the K-coronal dynamics. In a short survey of the research on the corona continuum color, the inconsistency of earlier results is noted (Section 1). The definition of the color index for the coronal continuum is given, the need to use the relative color index (RCI) is justified, and the expected RCI values are estimated with respect to the electron velocity (Section 2). In Section 3, it is noted that the orientation of 2D RCI distributions relative to the ecliptic plane or heliospheric current sheet can be the decisive argument for the K or F components. Section 4 presents the 2D RCI distributions for the coronas on July 11, 1991, and March 29, 2006; they reveal that the spectra of the corona and photosphere differ, with bluing near the limb at distances of <1.2 R_☉ and reddening with the distance over the entire corona at all position angles. It is noted that these distributions are the first observational corroborations of theoretical calculations by Reginald et al. (2009) on the shift of the continuum spectrum to the red side due to the electron fluxes propagating from the Sun in the entire coronal volume. The main results are briefly outlined in the Conclusions.

2 RELATIVE COLOR INDEX OF THE CONTINUUM

We used the broadband-filter method, which involves the registration of the corona in the red and blue spectrum ranges per frame. The description of the method and equipment, the use of broadband filters and color photofilms or color CCD as radiation receivers, and the TSE circumstances were presented earlier (Kim et al., 2011; Kim et al., 2017; Kim and Krusanova, 2020). We briefly recall the principal features of our approach:

(i) Refusal to use absolute calibration by the crescent Sun during partial phases carried out at heights and at time instants different from heights and instants of coronal registration during the total solar eclipse. This leads to ambiguity in the accounting for the transmission of the Earth’s atmosphere. We used a reference region with dimensions of <[40ʺ × 40ʺ] located near the Sun’s limb, as a rule, over the polar region for which the expected radial electron velocity is minimal. This is the crucial component of our approach;

(ii) Refusal to use neutral radial filters with selective transmittance;

(iii) Refusal to use spectral methods that require knowledge of the dependence of the instrument background on the wavelength.

Recall that the filter method is based on the comparison of images in the blue and red spectrum intervals and the introduction of the so-called color index, which is defined by different authors in indifferent ways but always includes the ratio of intensities (brightnesses) in the red and blue spectrum intervals. In our case, we introduced the concepts of the color index C and relative color index (RCI), which are defined by the expressions

$$C = \frac{{{{I_{{{\text{red}}}}^{{{\text{cor}}}}} \mathord{\left/ {\vphantom {{I_{{{\text{red}}}}^{{{\text{cor}}}}} {I_{{{\text{blue}}}}^{{{\text{cor}}}}}}} \right. \kern-0em} {I_{{{\text{blue}}}}^{{{\text{cor}}}}}}}}{{{{I_{{{\text{red}}}}^{{{\text{ph}}}}} \mathord{\left/ {\vphantom {{I_{{{\text{red}}}}^{{{\text{ph}}}}} {I_{{{\text{blue}}}}^{{{\text{ph}}}}}}} \right. \kern-0em} {I_{{{\text{blue}}}}^{{{\text{ph}}}}}}}},\,\,\,\,{{C}_{{{\text{ref}}}}} = {{I_{{{\text{red}}}}^{{{\text{ref}}}}} \mathord{\left/ {\vphantom {{I_{{{\text{red}}}}^{{{\text{ref}}}}} {I_{{{\text{blue}}}}^{{{\text{ref}}}}}}} \right. \kern-0em} {I_{{{\text{blue}}}}^{{{\text{ref}}}}}},\,\,\,\,RCI = \frac{{{{I_{{{\text{red}}}}^{{{\text{cor}}}}} \mathord{\left/ {\vphantom {{I_{{{\text{red}}}}^{{{\text{cor}}}}} {I_{{{\text{blue}}}}^{{{\text{cor}}}}}}} \right. \kern-0em} {I_{{{\text{blue}}}}^{{{\text{cor}}}}}}}}{{{{C}_{{{\text{ref}}}}}}},$$

where $I_{{{\text{red}}}}^{{{\text{ph}}}}$, $I_{{{\text{blue}}}}^{{{\text{ph}}}}$, $I_{{{\text{red}}}}^{{{\text{cor}}}}$, and $I_{{{\text{blue}}}}^{{{\text{cor}}}}$ are the intensities in the red and blue spectral intervals of the photospheric and coronal spectra, respectively, and C_ref is the color index of the reference region. All values in the expressions are obtained simultaneously per frame during the total phase.

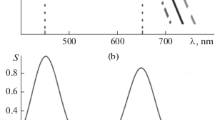
Let us estimate the expected values of the color index C. In the real corona, scattering electrons are those with V_e ≠ 0. For nonrelativistic electrons, one can expect a shift of the scattered spectrum due to the Doppler effect. Figure 1 (on the left) shows photospheric spectra (the solid black curve) and spectra scattered by an electron moving from the Sun with a speed of 10 000 km/s (the dashed line) and towards the Sun with a speed of 10 000 km/s (the dot-and-dash line), which is approximated with the Planck function. The vertical dot lines correspond to positions λ_max of the coronal continuum in the red and blue regions. On the right, from top to bottom, (I) the spectrum of the photospheric continuum, (S) the effective curves of broadband filters, and (I ') the coronal continuum in the red and blue spectrum regions are shown. The value C = 1.10 (0.93) corresponds to V_e = 100 000 km/s. The expected speeds are slower by an order of magnitude. Therefore, the introduction of the RCI improves the accuracy of the determination.

Fig. 1.

On the left: photospheric spectra (the solid black curve) and spectra scattered by an electron moving from the Sun with a speed of 10 000 km/s (the dashed line) and towards the Sun with a speed of 10 000 km/s (the dot-and-dash line) as approximated by the Planck function. The vertical dot lines correspond to positions λ_max of the coronal continuum in the red and blue regions. On the right, from top to bottom: (I) spectrum of the photospheric continuum, (S) effective curves of broadband filters, and (I ') coronal continuum in the red and blue spectrum regions.

Recall that we speak of thermal electrons. Koutchmy and Nikoghossian (2002) showed that nonthermal electrons can be diagnosed based on the determination of the color index.

3 DETERMINATION OF THE POSITION OF THE AVERAGED ECLIPTIC PLANE AND HCS

The color of the white-light corona depends on the color of its main components (K and F coronas) and their contribution to the total coronal emission. Observations of the radial velocity field of the circumsolar dust in the F corona (Aimanov et al., 1995) demonstrate that the main dust mass is concentrated in the ecliptic plane. The K-coronal structure is determined mainly by the presence of large-scale, helmet-shaped streamers that form a closed belt around the Sun. In general, the belt corresponds to the base of the heliospheric current sheet (HCS). Therefore, the orientation of 2D RCI distributions relative to the ecliptic plane and HCS plane can present unambiguous information about the leading role of dust or electron fluxes in the formation of these distributions. To better understand which of the corona components is responsible for eventual changes in the color of the total corona emission, let us consider their global structure and determine positions of the HCS midplane and ecliptic plane for each eclipse.

The position of the HCS midplane correlates well with the dipole component of the general magnetic field of the Sun. The perpendicular to the HCS midplane passing through the Sun’s center can be defined as the HCS axis; the points of its intersection with the Sun’s surface can be defined as poles of the HCS or magnetic field of the Sun. The shape of the 3D corona slightly varies with time. For most the cycle, the corona is in the plane or basic state, during which the HCS plane is slightly inclined from the equator plane (<20°). The rest of the time it is in the excited state, when the inclination of the HCS plane can be considerable and reach 70° (Gulyaev, 1992). The HCS configuration can be described well by the neutral line of the interplanetary magnetic field on the source surface (2.5 and 3.5 R_☉). The line is calculated via the extrapolation of measurements of photospheric magnetic fields. The position of the HCS midplane for coronas of 1991 and 2006 was determined from Wilcox Solar Observatory data (http://wso.stanford.edu/synsourcel.html).

The position of the ecliptic plane was determined as follows. Let us introduce the notation in the equatorial coordinate system (hereinafter, lowercase letters denote unit vectors and their coordinates).

${{\vec {r}}^{{{\text{sun}}}}}$ is the unit radius vector of the Sun’s center;

$\vec {r}_{{\text{N}}}^{{{\text{sun}}}}$ is the unit radius vector of the of the North pole of the Sun’s axis;

$\vec {r}_{{\text{N}}}^{{{\text{ecl}}}}$ is the unit radius vector of the North pole of the ecliptic.

In the equatorial coordinate system, the angular coordinates of the Sun’s center at the instant of the eclipse (α^sun, δ^sun), the North pole of the Sun’s axis ($\alpha _{{\text{N}}}^{{{\text{sun}}}}$ = 286.13°, $\delta _{{\text{N}}}^{{{\text{sun}}}}$ = 63.87°), and the North pole of the ecliptic ($\alpha _{{\text{N}}}^{{{\text{ecl}}}}$ = 270°, $\delta _{{\text{N}}}^{{{\text{ecl}}}}$ = 66.5°) are related to Cartesian rectangular coordinates by the following relationships:

$$\begin{array}{*{20}{c}} {{{{\vec {r}}}^{{{\text{sun}}}}}\,\,\,\,\,\,\,\,\,\,\,\,}&{{{x}^{{{\text{sun}}}}} = {\text{cos(}}{{\delta }^{{{\text{sun}}}}}{\text{)cos(}}{{\alpha }^{{{\text{sun}}}}}{\text{)}}{\text{,}}} \\ {}&{{{y}^{{{\text{sun}}}}} = {\text{cos(}}{{\delta }^{{{\text{sun}}}}}{\text{)sin(}}{{\alpha }^{{{\text{sun}}}}}{\text{)}}{\text{,}}} \\ {}&{{{z}^{{{\text{sun}}}}} = {\text{sin(}}{{\delta }^{{{\text{sun}}}}}{\text{)}}{\text{,}}} \end{array}$$

(1)

$$\begin{array}{*{20}{c}} {\vec {r}_{{\text{N}}}^{{{\text{sun}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,}&{x_{{\text{N}}}^{{{\text{sun}}}} = {\text{cos}}(\delta _{{\text{N}}}^{{{\text{sun}}}}){\kern 1pt} {\text{cos}}(\alpha _{{\text{N}}}^{{{\text{sun}}}}),} \\ {}&{y_{{\text{N}}}^{{{\text{sun}}}} = {\text{cos}}(\delta _{{\text{N}}}^{{{\text{sun}}}}){\kern 1pt} {\text{sin}}(\alpha _{{\text{N}}}^{{{\text{sun}}}}),} \\ {}&{z_{{\text{N}}}^{{{\text{sun}}}} = {\text{sin}}(\delta _{{\text{N}}}^{{{\text{sun}}}}),} \end{array}$$

(2)

$$\begin{array}{*{20}{c}} {\vec {r}_{{\text{N}}}^{{{\text{ecl}}}}\,\,\,\,\,\,\,\,\,\,\,\,\,}&{x_{{\text{N}}}^{{{\text{ecl}}}} = {\text{cos}}(\delta _{{\text{N}}}^{{{\text{ecl}}}}){\kern 1pt} {\text{cos}}(\alpha _{{\text{N}}}^{{{\text{ecl}}}}),} \\ {}&{y_{{\text{N}}}^{{{\text{ecl}}}} = {\text{cos}}(\delta _{{\text{N}}}^{{{\text{ecl}}}}){\kern 1pt} {\text{sin}}(\alpha _{{\text{N}}}^{{{\text{ecl}}}}),} \\ {}&{z_{{\text{N}}}^{{{\text{ecl}}}} = {\text{sin}}(\delta _{{\text{N}}}^{{{\text{ecl}}}}).} \end{array}$$

(3)

The coordinate system in the image plane (Fig. 2, on the left) is defined as follows. The coordinate origin lies in the center of the Sun. The ordinate axis coincides with the projection of the Sun’s axis on the image plane ($\vec {R}_{{{\text{Np}}}}^{{{\text{sun}}}}$). The unit radius vector of the ordinate axis is $\vec {r}_{{{\text{Np}}}}^{{{\text{sun}}}}$. The abscissa axis coincides with the intersection line of the Sun’s equator plane and image plane; it is directed towards the West (W) point. The unit radius vector of the abscissa axis is $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r} _{{{\text{Wp}}}}^{{{\text{sun}}}}$. Vector $\vec {r}_{{{\text{Np}}}}^{{{\text{ecl}}}}$ is a unit radius vector codirectional with the projection of $\vec {r}_{{\text{N}}}^{{{\text{ecl}}}}$ on the image plane; ψ is the angle between the equator plane and ecliptic plane.

Fig. 2.

Determination of the position of the averaged ecliptic plane. To the left, determination of the coordinate system in the image plane. To the right, determination of the Sun’s axis projection on the image plane.

Let us find the projection of vector $\vec {r}_{{\text{N}}}^{{{\text{sun}}}}$ on the image plane ($\vec {R}_{{{\text{Np}}}}^{{{\text{sun}}}}$, Fig. 2 on the left):

$$\vec {R}_{{{\text{Np}}}}^{{{\text{sun}}}} = \vec {r}_{{\text{N}}}^{{{\text{sun}}}} - {{\vec {r}}^{{{\text{sun}}}}}({{\vec {r}}^{{{\text{sun}}}}},\vec {r}_{{\text{N}}}^{{{\text{sun}}}}),$$

(4)

where the scalar product (${{\vec {r}}^{{{\text{sun}}}}}$, $\vec {r}_{{\text{N}}}^{{{\text{sun}}}}$) is equal to cos φ and is calculated as follows:

$${\text{cos}}\varphi = ({{\vec {r}}^{{{\text{sun}}}}},\vec {r}_{{\text{N}}}^{{{\text{sun}}}}) = {{x}^{{{\text{sun}}}}}x_{{\text{N}}}^{{{\text{sun}}}} + {{y}^{{{\text{sun}}}}}y_{{\text{N}}}^{{{\text{sun}}}} + {{z}^{{{\text{sun}}}}}z_{{\text{N}}}^{{{\text{sun}}}}.$$

(5)

Unit vector $\vec {r}_{{{\text{Np}}}}^{{{\text{sun}}}}$, which is codirectional with vector $\vec {R}_{{{\text{Np}}}}^{{{\text{sun}}}}$, is equal to

$$\vec {r}_{{{\text{Np}}}}^{{{\text{sun}}}} = {{\vec {R}_{{{\text{Np}}}}^{{{\text{sun}}}}} \mathord{\left/ {\vphantom {{\vec {R}_{{{\text{Np}}}}^{{{\text{sun}}}}} {\left| {\vec {R}_{{{\text{Np}}}}^{{{\text{sun}}}}} \right|}}} \right. \kern-0em} {\left| {\vec {R}_{{{\text{Np}}}}^{{{\text{sun}}}}} \right|}},$$

(6)

where |$\vec {R}_{{{\text{Np}}}}^{{{\text{sun}}}}$|= $\sqrt {{{{(X_{{{\text{Np}}}}^{{{\text{sun}}}})}}^{2}} + {{{(Y_{{{\text{Np}}}}^{{{\text{sun}}}})}}^{2}} + {{{(Z_{{{\text{Np}}}}^{{{\text{sun}}}})}}^{2}}}$.

By construction, vector $\vec {r}_{{{\text{Np}}}}^{{{\text{sun}}}}$ is a basis vector of the coordinate system defined above in the image plane. The second basis vector, which is denoted as $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r} _{{{\text{Wp}}}}^{{{\text{sun}}}}$, is the orthogonal complement to vector $\vec {r}_{{{\text{Np}}}}^{{{\text{sun}}}}$ and is equal to the vector product [$\vec {r}_{{{\text{Np}}}}^{{{\text{sun}}}}$, ${{\vec {r}}^{{{\text{sun}}}}}$]:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r} _{{{\text{Wp}}}}^{{{\text{sun}}}} = [\vec {r}_{{{\text{Np}}}}^{{{\text{sun}}}},{{\vec {r}}^{{{\text{sun}}}}}] = \det \left| {\begin{array}{*{20}{c}} {\vec {i}}&{\vec {j}}&{\vec {k}} \\ {x_{{{\text{Np}}}}^{{{\text{sun}}}}}&{y_{{{\text{Np}}}}^{{{\text{sun}}}}}&{z_{{{\text{Np}}}}^{{{\text{sun}}}}} \\ {{{x}^{{{\text{sun}}}}}}&{{{y}^{{{\text{sun}}}}}}&{{{z}^{{{\text{sun}}}}}} \end{array}} \right|.$$

(7)

Calculating the determinant from (7), we find coordinates of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r} _{{{\text{Wp}}}}^{{{\text{sun}}}}$:

$$\begin{gathered} x_{{{\text{Wp}}}}^{{{\text{sun}}}} = y_{{{\text{Np}}}}^{{{\text{sun}}}}{{z}^{{{\text{sun}}}}} - z_{{{\text{Np}}}}^{{{\text{sun}}}}{{y}^{{{\text{sun}}}}}, \\ y_{{{\text{Wp}}}}^{{{\text{sun}}}} = z_{{{\text{Np}}}}^{{{\text{sun}}}}{{x}^{{{\text{sun}}}}} - x_{{{\text{Np}}}}^{{{\text{sun}}}}{{z}^{{{\text{sun}}}}}, \\ z_{{{\text{Wp}}}}^{{{\text{sun}}}} = x_{{{\text{Np}}}}^{{{\text{sun}}}}{{y}^{{{\text{sun}}}}} - y_{{{\text{Np}}}}^{{{\text{sun}}}}{{x}^{{{\text{sun}}}}}. \\ \end{gathered} $$

(8)

The projection of the ecliptic axis on the image plain ($\vec {R}_{{{\text{Np}}}}^{{{\text{ecl}}}}$), by analogy with $\vec {R}_{{{\text{Np}}}}^{{{\text{sun}}}}$, is

$$\vec {R}_{{{\text{Np}}}}^{{{\text{ecl}}}} = \vec {r}_{{\text{N}}}^{{{\text{ecl}}}} - {{\vec {r}}^{{{\text{sun}}}}}({{\vec {r}}^{{{\text{sun}}}}},\vec {r}_{{\text{N}}}^{{{\text{ecl}}}}),$$

(9)

where the scalar product (${{\vec {r}}^{{{\text{sun}}}}}$, $\vec {r}_{{\text{N}}}^{{{\text{ecl}}}}$) is calculated as follows:

$$({{\vec {r}}^{{{\text{sun}}}}},\vec {r}_{{\text{N}}}^{{{\text{ecl}}}}) = {{x}^{{{\text{sun}}}}}x_{{\text{N}}}^{{{\text{ecl}}}} + {{y}^{{{\text{sun}}}}}y_{{\text{N}}}^{{{\text{ecl}}}} + {{z}^{{{\text{sun}}}}}z_{{\text{N}}}^{{{\text{ecl}}}},$$

(10)

The corresponding unit vector $\vec {r}_{{{\text{Np}}}}^{{{\text{ecl}}}}$ codirectional to vector $\vec {R}_{{{\text{Np}}}}^{{{\text{ecl}}}}$ is

$$\vec {r}_{{{\text{Np}}}}^{{{\text{ecl}}}} = {{\vec {R}_{{{\text{Np}}}}^{{{\text{ecl}}}}} \mathord{\left/ {\vphantom {{\vec {R}_{{{\text{Np}}}}^{{{\text{ecl}}}}} {\left| {\vec {R}_{{{\text{Np}}}}^{{{\text{ecl}}}}} \right|}}} \right. \kern-0em} {\left| {\vec {R}_{{{\text{Np}}}}^{{{\text{ecl}}}}} \right|}},$$

(11)

where |$\vec {R}_{{{\text{Np}}}}^{{{\text{ecl}}}}$| = $\sqrt {{{{(X_{{{\text{Np}}}}^{{{\text{ecl}}}})}}^{2}} + {{{(Y_{{{\text{Np}}}}^{{{\text{ecl}}}})}}^{2}} + {{{(Z_{{{\text{Np}}}}^{{{\text{ecl}}}})}}^{2}}}$.

The angle ψ between the ecliptic plain and the solar equator (Fig. 2 on the right) is uniquely determined by the following system of equations:

$$\left\{ {\begin{array}{*{20}{c}} {\cos \psi = (\vec {r}_{{{\text{Np}}}}^{{{\text{ecl}}}},\vec {r}_{{{\text{Np}}}}^{{{\text{sun}}}})} \\ {\sin \psi = (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r} _{{{\text{Np}}}}^{{{\text{ecl}}}},\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {r} _{{{\text{Wp}}}}^{{{\text{sun}}}}).} \end{array}} \right.$$

(12)

4 2D RCI DISTRIBUTIONS

Figures 3 and 4 present the 2D RCI distribution for the coronas of 1991 and 2006, respectively. The North (N) is on the top; the East (E) is on the left. The figures show the Sun’s center and the limbs of the Sun (the dashed line) and Moon (the solid line). The RCI scale is presented: dark tones correspond to bluing (RCI < 1); light tones correspond to reddening (RCI > 1). Gray color shows regions for which RCI = 1 (identical corona and photosphere continua), as well as regions excluded from processing. The white line marks the position of the ecliptic plane; the black line notes the position of the HCS midplane. The rectangle in the northern polar region marks reference regions by which the normalization was carried out. At the upper right, these regions are shown on a larger scale. the corona structure is shown on the right.

Fig. 3.

Two-dimensional distribution of the RCI for the corona in 1991 (left) and the corona structure (right).

Fig. 4.

Two-dimensional distribution of the RCI for the corona in 2006 (left) and the corona structure (right).

For the corona of 1991, the reference region with RCI = 1 was chosen in the gap between the structures identified with polar brushes: P (position angle) = 350°, R = 1.15–1.18_☉. The angle between the ecliptic plane and the solar equator was 3.6°; the inclination of the HCS midplane to the solar equator plane was 67°. The 2D RCI distribution for the corona of 1991 has a prolate shape oriented approximately symmetrically with respect to the HCS midplane. Such orientation of the 2D RCI distribution with respect to the HCS excludes the contribution of the dust component.

For the corona of 2006, the reference region with RCI = 1 was also chosen in the gap between the brushes in the northern polar regions: P = 10°, R = 1.12–1.15 R_☉. The angle between the ecliptic plane and the solar equator was 6°; the inclination of the HCS midplane to the solar equator plane was 8°. Therefore, the HCS midplane and the ecliptic plane are oriented near the solar equator plane. The 2D RCI distribution is oriented approximately symmetrically with respect to these planes.

Both 2D distributions reveal reddening with distance over the entire corona at all position angles. These are the first observational corroborations of the theory by Reginald et al. (2009). Note the presence of the diffusive and structural components, the correlation with the coronal structure, and the effect of bluing within a range of <1.3 R_☉.

5 CONCLUSIONS

The 2D distributions of the RCI in the continua of K coronas of July 11, 1991, and March 29, 2006, reveal the following:

(i) A difference in the energy distributions in the continuums of the K-corona and photosphere;

(ii) The presence of diffusive and structural components and different RCI values for different coronal structures;

(iii) Approximate symmetry of 2D RCI distributions with respect to the HCS projection on the image plane, which excludes the contribution of the dust component;

(iv) Reddening with the distance over the entire corona at all position angles, which makes it possible to consider RCI as an indicator of the corona broadening;

(v) Bluing at distances of <1.3 R_☉ due to scattering by bound ion electrons.

Thus, studies of the K-corona color provide information about the dynamics of the electron component of the coronal plasma and composition of the coronal matter.