Analysis of the Flight Data on Convective and Radiative Heating of the Surface of Martian Schiaparelli Descent Space Vehicle

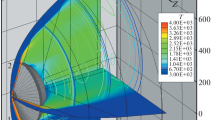
Abstract

Radiative aerothermodynamics of the Schiaparelli descent space vehicle are investigated numerically at some characteristic trajectory points in the process of its entry into the Martian atmosphere. The calculations are carried out using the three-dimensional radiative-gas dynamic model that describes flow of a viscous, compressible, heat-conductive, chemically reacting and radiative gas with regard to excitation of the vibrational degrees of freedom. In accordance with the computational data obtained, the maximum level of radiative heating of the back cover of the space entry vehicle is fixed at the trajectory point that corresponds to the flight velocity of ~2.6 km/s and amounts to 70% of total heating. The results of numerical simulation testify on the low intensity of chemical reactions for the trajectory points corresponding to the altitudes of 28–23 km. The data obtained for the radiative and total heat flux distributions over the spacecraft surface are in satisfactory agreement with the results of flight experiment.

The beginning of the Mars’ investigations by spacecraft was started by launching automatic interplanetary stations in the USSR in 60th years of last century. The implementation of the first successful landing on the planetary surface became the significant result of the Soviet program “Mars.” The successive stage of studying Mars is characterized by the implementation of research programs starting from the middle of 1990th years. The Pathfinder (1996) [1] and Mars Science Laboratory (MSL, 2011) [2] space vehicles have performed entry into the Martian atmosphere at the velocities of 7.65 and 5.8 km/s, respectively, and reached the planetary surface. Unique sets of experimental data were obtained in the process of passing through the dense atmospheric layers. These data underlie the significant number of calculated and theoretical studies directed to the creation and development of the computing models of aerodynamics and aerophysics with the aim to carry out the numerical simulation on key themes, namely, flow past the descent space vehicle surface, including the investigation of separation flows [3]; the problem of reliable prediction of convective heating of both the front shield and the back cover of the descent space vehicle [4]; the problem of choice of the models of physical and chemical kinetics [5] and vibrational relaxation; and estimation of the effect of turbulence on heat transfer [6]. The significant radiative ability of the basic components of the Martian atmosphere (such as CO₂) makes the problem of estimation of the radiative heating of the space entry vehicle surface to be very topical. In [7] it was first revealed that a considerable volume of high-temperature radiative gas in the wake behind the vehicle causes significant radiative heat flux (1–2 W/cm²) to the leeward part of the Martial descent space vehicle. Thus, obtaining the flight data on the level of heating the leeward part of the descent space vehicle was of particular importance.

This question was one of the most priority in the course of preparation to launching the Schiaparelli entry vehicle [8] whose experimental equipment included the set of three combined sensors (COMARS+) that ensured the measurements of the pressure and the temperature on the descent space vehicle surface, the total heat flux (total value of convective and radiative heating). The radiative heat flux which was measured by the broadband radiometer located, together with the remaining probes, on the leeward side of the space entry vehicle [8]. For this vehicle information on the trajectory of motion in the Martian atmosphere was given by a set of points that include the altitudes H ~ 82 and H ~ 28–11 km. Such a discreteness is attributable to communication blackout fixed over the range H ~ 82–28 km. The experimental data obtained at ten trajectory points are of significant interest for validation of various numerical models.

The present study is the continuation of the cycle of publications [9–11] devoted to radiative gas dynamics of the Martian entry vehicles. The results of computational investigation for the Exomars entry vehicle obtained in [9] demonstrate the significant level of the radiative heat flux whose fraction for individual trajectory points can be greater than the convective heat flux for the leeward side of the space entry vehicle. Within the framework of study [10], the algebraic turbulence models were validated with reference to the results of the stand experiment on perfect-gas flow past the front shield of the MSL space entry vehicle. In [11] the use of the 18-component model of dissociation and ionization made it possible to obtain confirmation of the effect of communication blackout for the trajectory fragments that correspond to the dense atmospheric layers.

The aim of the present study is to validate the chosen numerical model by means of computational interpretation of the flight data on heating the back cover of the Schiaparelli entry vehicle at various trajectory points.

SYSTEM OF GOVERNING EQUATIONS

Within the framework of the present study, we employed the three-dimensional radiative gas dynamics model [9] adapted to carry out calculations with the use of multiblock structured grids. The model includes the gas dynamics equations (continuity and Navier–Stokes equations), as well as the energy conservation equations of the molecular translational motion and vibrational energy, the mass conservation equations for the components of mixture, and the radiation transport equation:

$$\frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \rho u}}{{\partial x}} + \frac{{\partial \rho {{\upsilon }}}}{{\partial y}} + \frac{{\partial \rho {\text{w}}}}{{\partial z}} = 0,$$

(1.1)

$$\frac{{\partial \rho u}}{{\partial t}} + {\text{div}}\left( {\rho u{\mathbf{V}}} \right) = - \frac{{\partial p}}{{\partial x}} - \frac{2}{3}\frac{\partial }{{\partial x}}\left( {\mu {\text{div}}{\mathbf{V}}} \right) + 2\frac{\partial }{{\partial x}}\left( {\mu \frac{{\partial u}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left[ {\mu \left( {\frac{{\partial v}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)} \right] + \frac{\partial }{{\partial z}}\left[ {\mu \left( {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right)} \right],$$

(1.2)

$$\frac{{\partial \rho {v}}}{{\partial t}} + {\text{div}}\left( {\rho {v}{\mathbf{V}}} \right) = - \frac{{\partial p}}{{\partial y}} - \frac{2}{3}\frac{\partial }{{\partial y}}\left( {\mu {\text{div}}{\mathbf{V}}} \right) + 2\frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial {v}}}{{\partial y}}} \right) + \frac{\partial }{{\partial x}}\left[ {\mu \left( {\frac{{\partial {v}}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)} \right] + \frac{\partial }{{\partial z}}\left[ {\mu \left( {\frac{{\partial w}}{{\partial y}} + \frac{{\partial {v}}}{{\partial z}}} \right)} \right],$$

(1.3)

$$\frac{{\partial \rho w}}{{\partial t}} + {\text{div}}\left( {{{\rho }}w{\mathbf{V}}} \right) = - \frac{{\partial p}}{{\partial z}} - \frac{2}{3}\frac{\partial }{{\partial z}}\left( {{{\mu \text{div}}}{\mathbf{V}}} \right) + 2\frac{\partial }{{\partial z}}\left( {{{\mu }}\frac{{\partial w}}{{\partial z}}} \right) + \frac{\partial }{{\partial x}}\left[ {{{\mu }}\left( {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}}} \right)} \right] + \frac{\partial }{{\partial y}}\left[ {{{\mu }}\left( {\frac{{\partial w}}{{\partial y}} + \frac{{\partial {v}}}{{\partial z}}} \right)} \right],$$

(1.4)

$$\begin{gathered} \rho {{c}_{p}}\frac{{\partial T}}{{\partial t}} + \rho {{c}_{p}}{\mathbf{V}}\operatorname{grad} T = \operatorname{div} \left( {\lambda \operatorname{grad} T} \right) + \frac{{\partial p}}{{\partial t}} + {\mathbf{V}}\operatorname{grad} p + {{\Phi }_{\mu }} + {{Q}_{{{\text{vib}}}}} - \operatorname{div} {{{\mathbf{q}}}_{R}} \\ \, - \sum\limits_{i = 1}^{{{N}_{s}}} {{{h}_{i}}{{{\dot {w}}}_{i}}} + \sum\limits_{i = 1}^{{{N}_{s}}} {\rho {{c}_{{p,i}}}{{D}_{i}}} \left( {\operatorname{grad} {{Y}_{i}} \times \operatorname{grad} T} \right), \\ \end{gathered} $$

(1.5)

$$\frac{{\partial \rho {{e}_{{{\text{v}},m}}}}}{{\partial t}} + \operatorname{div} \left( {\rho {\mathbf{V}}{{e}_{{{\text{v}},m}}}} \right) = {{\dot {e}}_{{{\text{v}},m}}},\quad m = 1,2, \ldots ,{{N}_{{\text{V}}}}.$$

(1.6)

In Eqs. (1.1)–(1.6) we have: $\rho$ is the density, t is time, $x,y,z$ are the coordinates, $u,{v},w$ are the projections of the velocity vector V, p is the pressure, $\mu$ is the dynamic viscosity coefficient, c_p is the heat capacity at constant pressure, $T$ is the temperature, $\lambda$ is the thermal conductivity, ${{{\mathbf{q}}}_{R}}$ is the vector of density of the radiative heat flux, ${{Q}_{{{\text{vib}}}}}$ is the volume heat release caused by the vibrational relaxation processes, h_i is the specific enthalpy of the ith component, ${{\dot {w}}_{i}}$ is the mass rate of formation of the ith component in unit volume, ${{N}_{s}}$ is the number of the components of mixture, ${{c}_{{p,i}}}$, ${{D}_{i}}$, and ${{Y}_{i}}$ are the heat capacity at constant pressure, the diffusion coefficient, and the relative mass number density of the ith component of mixture, respectively, ${{e}_{{{\text{v}},m}}}$ is the specific vibrational energy of the mth vibrational mode, ${{N}_{V}}$ is the number of vibrational modes, ${{\dot {e}}_{{{\text{v}},m}}}$ is the relaxation change in the vibrational energy in the mth mode which can be determined by means of the Landau–Teller formula

$${{\dot {e}}_{{{\text{v}},m}}} = {{\rho }_{{i(m)}}}\frac{{e_{{{\text{v}},m}}^{0} - {{e}_{{{\text{v}},m}}}}}{{{{\tau }_{m}}}} - {{e}_{{{\text{v}},m}}}{{\dot {w}}_{{i(m)}}}.$$

(1.7)

In turn, the quantity ${{e}_{{{\text{v}},m}}}$ is calculated from the folloing formula:

$${{e}_{{{\text{v}},m}}} = \frac{{{{R}_{0}}{{\theta }_{m}}}}{{{{M}_{{i(m)}}}\left[ {\exp \left( {{{{{\theta }_{m}}} \mathord{\left/ {\vphantom {{{{\theta }_{m}}} {{{T}_{{V,m}}}}}} \right. \kern-0em} {{{T}_{{V,m}}}}}} \right) - 1} \right]}}.$$

(1.8)

In Eqs. (1.7)–(1.8)${{\rho }_{{i(m)}}}$ and ${{\dot {w}}_{{i(m)}}}$ are the density and the mass rate of formation of the ith component that has the mth vibrational mode, $e_{{{\text{v}},m}}^{0} = {{e}_{{{\text{v}},m}}}({{T}_{V}} = T)$ is the specific equilibrium energy of motion in the mth vibrational mode of the ith component, τ_m is the vibrational relaxation time of the mth mode, R₀ is the universal gas constant, θ_m is the characteristic vibrational temperature of the mth mode, ${{M}_{{i(m)}}}$ is the molecular mass of the ith component, and ${{T}_{{V,m}}}$ is the vibrational temperature in the mth vibrational mode. The vibrational kinetics model includes five vibrational modes [12]: O₂, the CO₂ symmetric mode, the CO₂ antisymmetric mode, the CO₂ deformation mode, and СО. It should be noted that within the framework of the present study CO₂ is the single component of the Martian atmosphere. In [9] the questions of application of chemical and vibrationalk kinetics models which inlude the nitrogen components were considered. As a whole, taking N₂ into account does not affect appreciably the basic aerothermodynamic characteristics.

In Eq. (1.5) Φ_μ is the dissipative function defined as follows:

$${{\Phi }_{\mu }} = \mu \left[ {2{{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}}^{2}} + 2{{{\left( {\frac{{\partial v}}{{\partial y}}} \right)}}^{2}} + 2{{{\left( {\frac{{\partial w}}{{\partial z}}} \right)}}^{2}} + } \right.{{\left( {\frac{{\partial v}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)}^{2}} + {{\left( {\frac{{\partial w}}{{\partial y}} + \frac{{\partial v}}{{\partial z}}} \right)}^{2}} + \left. {{{{\left( {\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)}}^{2}} - \frac{2}{3}{{{\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right)}}^{2}}} \right].$$

The model also contains the mass conservation equation for individual components of mixture

$$\frac{{\partial {{\rho }_{i}}}}{{\partial t}} + \operatorname{div} {{\rho }_{i}}{\mathbf{V}} = - \operatorname{div} {{{\mathbf{J}}}_{i}} + {{\dot {w}}_{i}},\quad i = 1,2, \ldots ,{{N}_{s}}.$$

(1.9)

Here, ρ_i is the density of the ith component of mixture and ${{{\mathbf{J}}}_{i}} = - \rho {{D}_{i}}{\text{grad}}{{Y}_{i}}$ is the mass diffusibe flux of the ith component.

In the calculations we used the 6-component (С, O, C₂, O₂, CO, and CO₂) chemical kinetics model that inludes 28 chemical reactions [12]. In symbolic form the equations of chemical kinetics can be written as follows:

$$\sum\limits_{i = 1}^{{{N}_{s}}} {{{a}_{{i,n}}}\left[ {{{X}_{i}}} \right]} = \sum\limits_{i = 1}^{{{N}_{s}}} {{{b}_{{i,n}}}\left[ {{{X}_{i}}} \right]} ,\quad n = 1,2, \ldots ,{{N}_{r}}.$$

Here, ${{a}_{{i,n}}}$ and ${{b}_{{i,n}}}$ are the stoichiometric coefficient of the nth chemical reaction, $\left[ {{{X}_{i}}} \right]$ are the symbols of the reagents and products of the chemical reaction, and N_r is the number of chemical reactions. The rate of formation of the ith component in the nth chemical reaction is detimened as follows:

$${{\left( {\frac{{{\text{d}}{{X}_{i}}}}{{{\text{d}}t}}} \right)}_{n}} = {{k}_{{f,n}}}\left( {{{b}_{{i,n}}} - {{a}_{{i,n}}}} \right)\prod\limits_{i = 1}^{{{N}_{s}}} {{{X}_{i}}^{{{{a}_{{i,n}}}}}} - {{k}_{{r,n}}}\left( {{{b}_{{i,n}}} - {{a}_{{i,n}}}} \right)\prod\limits_{i = 1}^{{{N}_{s}}} {{{X}_{i}}^{{{{b}_{{i,n}}}}}} = \left( {{{b}_{{i,n}}} - {{a}_{{i,n}}}} \right)(S_{{f,i}}^{n} - S_{{r,i}}^{n}).$$

In the previous equation ${{k}_{{f,n}}}$ and ${{k}_{{r,n}}}$ are the forward and reverse reaction rate constants, and $S_{{f,i}}^{n}$ and $S_{{r,i}}^{n}$ are the forward and reverse reaction rates. The mass rate of chemical transformations for the ith component of mixture can be calculated by means of the following relation:

$${{\dot {w}}_{i}} = {{M}_{i}}{{W}_{i}} = \sum\limits_{n = 1}^{{{N}_{r}}} {\left( {{{b}_{{i,n}}} - {{a}_{{i,n}}}} \right)(S_{{f,i}}^{n} - S_{{r,i}}^{n})} .$$

The forward and reverse reaction rate constants are determined from the Arrhenius formula

$${{k}_{{f(r),n}}} = {{A}_{{f(r),n}}}{{T}^{{{{n}_{{f(r),n}}}}}}\exp \left( { - \frac{{{{E}_{{f(r),n}}}}}{{kT}}} \right).$$

In this relation ${{k}_{{f(r),n}}}$, ${{A}_{{f(r),n}}}$, and ${{E}_{{f(r),n}}}$ are the approximating coefficients for the forward and reverse reactions and k is the Boltzmann constant.

The radiation transport equation is formulated in the multigroup approximation without regard for scattering and has the following form:

$$\boldsymbol\Omega \frac{{\partial {{J}_{\omega }}\left( {{\mathbf{r}},\boldsymbol\Omega } \right)}}{{\partial {\mathbf{r}}}} + {{\kappa }_{\omega }}\left( {\mathbf{r}} \right){{J}_{\omega }}\left( {{\mathbf{r}},\boldsymbol\Omega } \right) = {{j}_{\omega }}\left( {\mathbf{r}} \right).$$

(1.10)

In this equation $\boldsymbol\Omega$ is the directional vector, r is the radius vector, ${{J}_{\omega }}\left( {{\mathbf{r}},\boldsymbol\Omega } \right)$ is the spectral radiation intensity, ${{\kappa }_{\omega }}\left( {\mathbf{r}} \right)$ is the spectral absorption coefficient, and ${{j}_{\omega }}\left( {\mathbf{r}} \right)$ is the spectral volume radiation value. The Kirchhoff law is used for calculating the spectral volume radiation value in the approximation of local thermodynamic equilibrium

$${{j}_{\omega }}\left( {\mathbf{r}} \right) = {{\kappa }_{\omega }}\left( {\mathbf{r}} \right){{J}_{{b,\omega }}}\left( {\mathbf{r}} \right)$$

Here, ${{J}_{{b,\omega }}}\left( {\mathbf{r}} \right)$ is the spectral radiation intensity of the perfectly black body. The integral radiative heat flux is calculated from the formula

$${\mathbf{q}_{R}} = \int\limits_{4\pi } {d\Omega } \int\limits_{\Delta {{\omega }_{{tot}}}} {{{J}_{\omega }}\left( {{\mathbf{r}},\boldsymbol\Omega } \right)\boldsymbol\Omega d} \omega = \int\limits_{\Delta {{\omega }_{{tot}}}} {{\mathbf{q}_{{R,\omega }}}\left( {\mathbf{r}} \right)d} \omega {\kern 1pt} {\kern 1pt} .$$

The viscosity and thermal conductivity coefficients of gas mixture are calculated using the Chapman–Enskog method [13]

$$\begin{gathered} \mu = {1 \mathord{\left/ {\vphantom {1 {\sum\limits_{i = 1}^{{{N}_{s}}} {\left( {{{{{Y}_{i}}} \mathord{\left/ {\vphantom {{{{Y}_{i}}} {{{\mu }_{i}}}}} \right. \kern-0em} {{{\mu }_{i}}}}} \right)} }}} \right. \kern-0em} {\sum\limits_{i = 1}^{{{N}_{s}}} {\left( {{{{{Y}_{i}}} \mathord{\left/ {\vphantom {{{{Y}_{i}}} {{{\mu }_{i}}}}} \right. \kern-0em} {{{\mu }_{i}}}}} \right)} }}, \\ \lambda = \frac{1}{2}\left[ {\sum\limits_{i = 1}^{{{N}_{s}}} {{{x}_{i}}{{\lambda }_{i}}} + {1 \mathord{\left/ {\vphantom {1 {\sum\limits_{i = 1}^{{{N}_{s}}} {\left( {{{{{x}_{i}}} \mathord{\left/ {\vphantom {{{{x}_{i}}} {{{\lambda }_{i}}}}} \right. \kern-0em} {{{\lambda }_{i}}}}} \right)} }}} \right. \kern-0em} {\sum\limits_{i = 1}^{{{N}_{s}}} {\left( {{{{{x}_{i}}} \mathord{\left/ {\vphantom {{{{x}_{i}}} {{{\lambda }_{i}}}}} \right. \kern-0em} {{{\lambda }_{i}}}}} \right)} }}} \right], \\ \end{gathered} $$

$$\begin{gathered} {{\mu }_{i}} = 2.67 \times {{10}^{{ - 5}}}\frac{{\sqrt {{{M}_{i}}{{T}_{i}}} }}{{\sigma _{i}^{2}\Omega _{i}^{{(2,2)*}}}}, \\ {{\lambda }_{i}} = 8330\sqrt {\frac{{{{T}_{i}}}}{{{{M}_{i}}}}} \frac{1}{{\sigma _{i}^{2}\Omega _{i}^{{(2,2)*}}}}. \\ \end{gathered} $$

The effective diffusion coefficient is detemined from the Wilke formula [14]

$${{D}_{i}} = \frac{{1 - {{x}_{i}}}}{{\sum\limits_{j \ne i}^{{{N}_{s}}} {\left( {{{{{x}_{j}}} \mathord{\left/ {\vphantom {{{{x}_{j}}} {{{D}_{{ij}}}}}} \right. \kern-0em} {{{D}_{{ij}}}}}} \right)} }},$$

$${{D}_{{ij}}} = 1.858 \times {{10}^{{ - 3}}}\sqrt {T_{{^{i}}}^{3}\frac{{{{M}_{i}} + {{M}_{j}}}}{{{{M}_{i}}{{M}_{j}}}}} \,\frac{1}{{p\sigma _{{i,j}}^{2}\Omega _{{i,j}}^{{(1,1)*}}}}.$$

Here, σ_i is the effective collision diameter, x_i is the relative mole concentration of components, ${{T}_{i}} = {{kT} \mathord{\left/ {\vphantom {{kT} {{{\varepsilon }_{i}}}}} \right. \kern-0em} {{{\varepsilon }_{i}}}}$, ${{\varepsilon }_{i}}$ is a constant that characterizes the interaction potential, and $\Omega _{{i,j}}^{{(1,1)*}}$ and $\Omega _{i}^{{(2,2)*}}$ are the collision integrals calculated from the approximation relations [15]

$$\Omega _{{i,j}}^{{(1,1)*}} = 1.074T_{{i,j}}^{{ - 0.1604}},$$

$$\Omega _{{i,j}}^{{(2,2)*}} = 1.157T_{i}^{{ - 0.1472}},$$

where ${{T}_{{i,j}}} = {{kT} \mathord{\left/ {\vphantom {{kT} {{{\varepsilon }_{{i,j}}}}}} \right. \kern-0em} {{{\varepsilon }_{{i,j}}}}}$, ${{\varepsilon }_{{i,j}}} = \sqrt {{{\varepsilon }_{i}}{{\varepsilon }_{j}}}$, and ${{\sigma }_{{i,j}}} = \frac{1}{2}\left( {{{\sigma }_{i}} + {{\sigma }_{j}}} \right)$.

The equation of state of a perfect gas

$$p = \rho \frac{{{{R}_{0}}}}{{{{M}_{\Sigma }}}}T = \rho {{R}_{0}}T\sum\limits_i^{{{N}_{s}}} {\frac{{{{Y}_{i}}}}{{{{M}_{i}}}}} $$

is used as the closing relation.

The well-known approximations of the thermodynamic propertiies of individual substances [16] are used to calculate the equilibriun constants.

NUMERICAL METHOD

In [12] the numerical method of solving the system of equations (1.1)–(1.6), (1.9)–(1.10) is described in detail. The use of hydride explicit-implicit method underlies the computational technique. The AUSM finite-difference scheme is used to integrate the gas dynamics equations. The equations of conservation of the translational motion, the vibrational energy, and the continuity equations for individual components of mixture are integrated using an implicit finite-difference scheme [12]. The radiation transport equation is integrated using the Ray-tracing method [12].

RESULTS OF NUMERICAL SIMULATION

The three-dimensional calculations were carried out for the trajectory points S1–S4 whose parameters are given in Table 1. As compared with the known trajectories of the Mars Pathfinder and MSL entry vehicles, in the case of the Schiaparelli space entry vehicle the flight velocity ~5.8 km/s is fixed at the altitude ~82 km. This corresponds to considerably more rarefied atmosphere.

Table 1. Trajectory parameters for the Schiaparelli entry vehicle [8]

In Fig. 1 we have reproduced the distributions of the main gas dynamic parameters that reflect the characteristic structure of the flow field which includes the compressed zone of the shock layer, the high-temperature gas dynamic wake, and the separated reverse-recirculation flow zone whose streamlines are shown in Fig. 1c. It should be noted that the large-scale vortex structure was formed in the immediate neighborhood of the supposed place of location of the heat flux sensors. This complicates significantly the obtaining of steady-state solution for this region of the flow field. For the unknown free-stream parameters the shock stand-off from the entry vehicle surface is not greater than 3 cm. For the considered fragment of trajectory the temperature is higher than 8000 K in the neighborhood of the shock wave, while for the wake the temperature is recorded at the level higher than 2500 K. In the flow behind the space vehicle the pressure distribution is characterized by the high level of homogeneity. Local rarefaction is observed in the zone of direct flow separation.

Fig. 1.

Distributions of the translational temperature (a), the dimensionless pressure ${\text{Pres}} = {p \mathord{\left/ {\vphantom {p {{{\rho }_{\infty }}}}} \right. \kern-0em} {{{\rho }_{\infty }}}}V_{\infty }^{2}$ (b), and the longitudinal velocity component (c) at the trajectory point S1.

In Fig. 2 we have reproduced the distributions of the CO₂ and СО mole fractions obtained with the use of the approximations of catalytic and non-catalytic surfaces. The maximum change in the concentrations of the components of mixture can be seen in the region of front shield; however, the effect of the catalytic conditions on the surface manifests itself mainly in the wake behind the entry vehicle from the windward side. In this zone the CO concentration increases significantly with simultaneous decrease in the CO₂ concentration. These components of mixture are optically active and the calculation of their concentrations is crucial in estimating the radiative heat flux. Under the conditions of rarefied atmosphere, for all types of the surface the level of the minimum CO₂ concentration amounts to ~60%, while the maximum values of CO mole fractions reach 25%.

Fig. 2.

Distributions of the CO₂ and CO mole fractions for the catalytic (a and c) and non-catalytic (b and d) surfaces.

The flow under the conditions that correspond to the trajectory point S1 is characterized by considerable thermal nonequilibrium. This is reflected in the translational and vibrational temperature distributions shown in Fig. 3. The effect of rareness of the medium is manifested in smoothness of the temperature profiles and absence of the characteristic peak in the shock-wave zone.

Fig. 3.

Distributions of the translational and vibrational temperatures along the leading critical streamline at the trajectory point S1. Curve 1 corresponds to the translational temperature, curve 2 to the temperature of the O₂ mode, curve 3 to the temperature of the CO₂ deformational mode, curve 4 to the temperature of the CO₂ antisymmetric mode, curve 5 to the temperature of the CO₂ symmetric mode, and curve 6 to the temperature of the CO mode.

Despite the high velocity and significant (higher than 2500 K) temperature in the wake, for the trajectory point S1 we can note fairly low degree of heating of the rear part of the Schiaparelli entry vehicle at the radiative heat flux ~0.06 W/cm² (Fig. 4). This section of trajectory is characterized by predominance of the convective heating over the radiative heating along the entire vehicle surface. In the case of non-catalytic approximation a certain reduction in the radiative heat flux in the leeward zone gives place to its increased value in the windward part of the entry vehicle. This is attributable to the higher CO concentration in this region of the flow field.

Fig. 4.

Heat flux distributions for the Schiaparelli entry vehicle. Curve 1 corresponds to the convective heat flux, curve 2 to the radiative heat flux for the catalytic surface, and curve 3 to the radiative heat flux for the non-catalytic surface.

The trajectory points downstream of the radioblocking zone correspond to the significantly lower temperature in the shock layer and in the wake behind the vehicle. Nevertheless, increase in the density of atmosphere at the altitudes of 28–23 km leads to the higher level of heating the entry vehicle surface. For points S2, S3, and S4 the maximum temperature along the leading critical streamline amounts to ~2600, 1800, and 1250 K, respectively (Fig. 5).

Fig. 5.

Distributions of the translational temperature at the trajectory points S2 (a), S3 (b), and S4 (c). The catalytic surface.

The shock-wave stand-off from the entry vehicle surface increases with decrease in the flight velocity. Thus, the width of the compressed layer zone in the neighborhood of the front shield increases from 5 cm at the altitude of 28 km to 8 cm at the altitude of 23 km.

In Fig. 6 we have reproduced the distributions of the CO₂ and CO mole fractions for the trajectory point S2. A slight change in the concentrations of components of gas mixture (not higher than 1%) is observed. In the process of descending in the atmosphere the intensity of chemical reactions reduces as well as the fraction of the diffusive heat flux in the convective heating of the entry vehicle. The vibrational degrees of freedom are not excited appreciably in these sections of trajectory. These factors make it possible to conclude on the possibility of correct estimation of the convective heat flux for the leeward part of the entry vehicle within the framework of the perfect gas model.

Fig. 6.

Distributions CO₂ (a) and CO (b) mole fractions at the trajectory point S2. The catalytic surface.

In Fig. 7 we have reproduced the distributions of the convective and radiative heat fluxes for the trajectory points S2–S4. At point S2 the radiative heating is predominant for the back cover of the Schiaparelli space entry vehicle and reaches the maximum value 1 W/cm² over the entire trajectory considered for the convective flux 0.2–0.75 W/cm². For the subsequent point we can note the comparable contribution of both components of the total heat flux at the level of 0.25–0.4 W/cm². The final point is characterized by the higher convective flux along the entire leeward part of the space entry vehicle.

Fig. 7.

Heat flux distributions at the trajectory points S2 (a), S3 (b), and S4 (c). Curve 1 corresponds to the convective heat flux and curve 2 to the radiative heat flux. The catalytic surface.

The calculation results were compared with the experimental data only for catalytic surface. The sensors locations were defined approximately in accordance with [8, 17]. In Fig. 8 we have shown the validation results.

Fig. 8.

Distribution of the radiative heat flux at the location of the radiometer (a) and distribution of the total heat flux at the location of the COMARS3 (b), COMARS2 (c), and COMARS1 (d) probes at the trajectory points S1–S4. 1 corresponds to the experimental data [8] and 2 to the calculations. The catalytic surface.

At each of the trajectory points a certain overestimation of the radiative heat flux is observed; however, this is characteristic of the calculation results of other authors (radiative heat flux is about 1.5 W/cm² [17]). At the point S2 it is necessary to take into account the length of the confidence interval of determination of the experimental parameters which is equal to ~0.15 W/cm² for both radiative and total heat fluxes [8]. Moreover, in [8] the values of the angles of attack were not defined concretely. This introduces an uncertainty in solution of the gas dynamic part of the problem. In [17] it was demonstrated that for the trajectory points S2–S4 the value of the angles of attack lies within 4°–7°. This was used within the framework of the present study. The location of the probes in the neighborhood of the separated flow zone (in particular, radiometer) is also the factor that affects the calculation accuracy. Despite the fact that the particular values of the convective heat flux are unknown, in accordance with the data of [8] for the location of the COMARS3 probe, approximate estimates can be made for the trajectory points S2–S4. These estimates show that the characteristic level of convective heating amounts to ~0.6 W/cm² for point S2, 0.4 W/cm² for point S3, and 0.25 W/cm² for point S4. The data obtained in the present study are fairly close to these values.

SUMMARY

Aerothermodynamics of the Schiaparelli entry vehicle are investigated numerically at four trajectory points with regard to surface radiative heating. It is shown that for the considered free-stream parameters heating of the leeward surface of the entry vehicle can mainly be determined by the radiative heat flux which reaches 1–2 W/cm² at point S2. It is demonstrated that the appreciable effect of chemical reactions on the distribution of the components of gas mixture is noted only at the trajectory point S1. The computational data obtained are in satisfactory agreement with both the exterior results and the data of flight experiment.