Many chemical engineering processes with the participation of the solid phase are accompanied by a change in the size of dispersed particles in such processes as agglomeration, breakup, abrasion, dissolution, etc. The change in the particle distribution with time undoubtedly influences the heat- and mass-transfer processes, and this should be taken into account in calculating their characteristics. Under intense flow conditions, these processes have a stochastic nature and cannot be quantitatively described at the level of an individual particle. Therefore, in developing a mathematical description of the change in the particle distribution, it is natural to use the apparatus of probability theory. Previously [1–7], such an approach demonstratively showed its efficiency in modeling processes of various physical nature with taking into account its specificity. However, the proposed [1–7] mathematical models are not universal (are partial). As a consequence, there are no reliable methods to quantitatively estimate the change in the particle size distribution and its effect on the main process.

In this work, a method was proposed to mathematically model the change in the solid-phase particle distribution with taking into account the specificity of phenomena (coagulation, breakup, abrasion, etc.) affecting the particle size.

The change in the particle distribution under the action of several phenomena of different physical nature can be quantitatively described using the superposition principle. According to this principle, the rate of the change in the particle mass distribution function is equal to the sum of the rates of individual processes:

$$\frac{{\partial F}}{{\partial t}} = \mathop \sum \limits_{i = 1}^k {{\left( {\frac{{\partial F}}{{\partial t}}} \right)}_{i}}.$$

Such an approach to mathematical modeling of processes represented by linear and quasi-linear differential and integro-differential equations enables one to describe a complex composite process by kinetic equations of individual simpler processes.

According to this approach, in the general case, the change in the solid-phase particle distribution in a continuous-flow or batch apparatus can be described by the equation [1]

$$\begin{gathered} \frac{{\partial f}}{{\partial t}} + \operatorname{div} (\bar {w} - {{D}_{p}}\vec {\nabla })f + \frac{\partial }{{\partial m}}\left( {u - \frac{\partial }{{\partial m}}{{D}_{m}}} \right)f \\ = {{I}^{ + }} - {{I}^{ - }}. \\ \end{gathered} $$
(1)

Equation (1) is essentially the material balance equation, where \(\vec {\nabla }f(\vec {r},m,t)\) is the particle mass (m) distribution function gradient. According to the physical meaning of the distribution function, the expression \(f(\vec {r},m,t)dm\) is the mean of the number of particles with masses in the range (m, m + dm) in unit volume of the working space of the apparatus in the neighborhood of the point with the radius vector \(\bar {r}\) at time t. In Eq. (1), \(\bar {w}\) is the mean velocity of the solid phase; Dp is the longitudinal dispersion coefficient of the solid phase; \(u(\vec {r},m,t)\) is the total mean rate of the continuous growth of particles, which can occur by both the accretion of small particles on large ones, and the deposition of the solid phase from solutions on their surface. The diffusion coefficient in the mass space, Dm, takes into account the fact that the growth rates of individual particles can be different. The terms I+ and I− on the right-hand side of the equation are responsible for the changes in the particle size by coagulation and breakup, respectively. If k(t, \(\bar {r}\), m, s) is the probability density of agglomeration of two particles of masses m and s in unit time, and g(t, \(\bar {r}\), m, m − s, s) is the probability density of breakup of a particle of mass m into two fragments of masses (m – s) and s, then the terms I+ and I– take the form [1]

$$\begin{gathered} {{I}^{ + }} = \frac{1}{2}\int\limits_0^m {k(t,\vec {r},m - s,s)f(\vec {r},m - s,t)f(\vec {r},s,t)ds} \\ + \;\int\limits_m^\infty {g(t,\vec {r},s;s - m,m)f(\vec {r},s,t)ds} , \\ \end{gathered} $$
(2)
$$\begin{gathered} {{I}^{ - }} = \left[ {\frac{1}{2}\int\limits_0^m {g(t,\vec {r},m;m - s,s)ds} } \right. \\ \left. { + \;\int\limits_0^\infty {k(t,\vec {r},m,s)f(\vec {r},s,t)ds} } \right]f(\vec {r},s,t). \\ \end{gathered} $$
(3)

Equations (1)–(3) are general and can be used to quantitatively describe the change in the solid-phase particle distribution for many chemical engineering processes under certain process conditions. Let us illustrate the said by a number of examples.

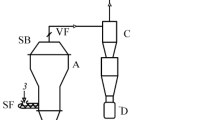
One of the important processes with a wide industrial use is fluidized-bed granulation from solutions and suspensions. From the standpoint of mathematical modeling, this is a complex process consisting of simpler ones, such as continuous growth by coagulation of large granules with small solution drops, breakup of granules, and their abrasion. Let us apply the approach we proposed to analyzing the granulation in a continuous-flow apparatus with a well-stirred solid phase. Let new granulation nuclei form by the breakdown of particles due to, e.g., their collisions of thermal stresses in the almost complete absence of coagulation and attrition. Such conditions are close to the conditions of the continuous fluidized-bed dehydration of solutions and suspensions. For steady-state conditions, Eq. (1) is significantly simplified:

$$\begin{gathered} \frac{d}{{dm}}u\varphi + \left[ {\frac{1}{T} + \frac{1}{2}\int\limits_0^m {g(m,m - s,s)ds} } \right]\varphi (m) \\ = \int\limits_m^\infty {g(s;s - m,m)\varphi (s)ds} . \\ \end{gathered} $$
(4)

Here, φ(m) is the particle mass distribution density: \(\varphi \) = \(\frac{{f(m)}}{N}\), \(\int_0^\infty {\varphi (m)dm} \) = 1, and N is the number of particles in the apparatus; and T is their mean residence time in the working space. It is natural to assume that the probability of breakup of a particle is proportional to its mass because, with increasing particle size, the sizes of heterogeneities inside the particle also increase. Then, the breakup probability density is constant: g(t, \(\bar {r}\), m, m − s, s) = g0 = const. In this case, Eq. (4) can be rewritten as

$$\frac{d}{{dm}}u\varphi + \frac{1}{T}\varphi (m) + \frac{1}{2}m{{g}_{0}}\varphi (m) = {{g}_{0}}\int\limits_m^\infty {\varphi (s)ds} .$$
(5)

Experimental studies showed that, in fluidized-bed granulation from solutions, the particle growth rate u(m) can be approximated by the expression

$$u = \frac{{dm}}{{dt}} = A{{m}^{n}},$$
(6)

where the constant А is found experimentally; and the exponent n takes the values from 0 to 1, depending on the design of the flow of the solid phase in the apparatus. In particular, n = 2/3 for a fluidized bed, and n = 1 for a spouted bed. Using dependence (6), Eq. (5) can be solved numerically, but it also can be solved analytically in the limiting cases where n = 0 and n = 1. The explicit form of these solutions shows the limiting behavior of the particle distribution functions in real-world processes. At n = 0, the solution of Eq. (5) that meets the condition φ(0) = 0 is the function

$$\varphi (m) = {{g}_{0}}T\left( {\xi + \frac{{{{\xi }^{2}}}}{2}} \right)\exp \left[ { - \left( {\xi + \frac{{{{\xi }^{2}}}}{2}} \right)} \right],$$
(7)

where \(\xi = \frac{m}{{\bar {m}}} = \frac{m}{{uT}}\) is a dimensionless parameter, and \(\bar {m}\) is the mean particle mass. Expression (7) allows one to determine any parameters of the solid-phase particle distribution at the outlet of the apparatus, which, in practice, is the main purpose of calculating the characteristics of any technological process.

At n = 1, when the particle growth rate is proportional to the particle size (u = Am), the solution of Eq. (5) obviously takes the form

$$\varphi (m) = \frac{{{{g}_{0}}}}{{2A}}\exp \left[ { - \frac{{{{g}_{0}}}}{{2A}}m} \right].$$
(8)

Another illustrative example of the efficiency of Eq. (1) in analyzing processes accompanied by a change in the solid-phase particle distribution can be the use of this equation to study coagulation of particles during treatment of powder materials. For the coagulation of particles in a well-stirred continuous-flow apparatus, Eq. (1) can be rewritten in a simpler form

$$\begin{gathered} \frac{{\partial f}}{{\partial t}} + \frac{1}{T}f + f\int\limits_0^\infty {k(m,s)f(s,t)ds} \\ = \frac{1}{T}{{f}_{0}}(m,t) + \frac{1}{2}\int\limits_0^m {k(m - s,s)f(m - s,t)f(s,t)ds} , \\ \end{gathered} $$
(9)

where f0(m, t) is the distribution function density of the incoming particle flow. If the probability density of coagulation of two particles is assumed to be constant: k(m, s) = k0 = const, then Eq. (9) under steady-state conditions can be represented as

$$\begin{gathered} f(m) = \frac{{{{N}_{0}}}}{{\sqrt {1 + 2T{{k}_{0}}{{N}_{0}}} }} \\ \times \;\sum\limits_{i = 1}^\infty {{{{\left( {\frac{{2T{{k}_{0}}{{N}_{0}}}}{{1 + 2T{{k}_{0}}{{N}_{0}}}}} \right)}}^{{i - 1}}}\frac{{2\Gamma \left( {i + \frac{1}{2}} \right)}}{{\sqrt \pi (2i - 1)\Gamma (i + 1)}}} , \\ \end{gathered} $$
(10)

where N0 is the number of particles entering the apparatus in unit time, and Γ(х) is the gamma function. Expression (10) enables one to calculate, in particular, the number of particles in the apparatus as a function of their mean residence time in the working space, determine their mean mass, and estimate the polydispersity of the coagulating system of particles. The last characteristic is determined by the relative variance, which, in the case under consideration, is

$${{\left( {\frac{\sigma }{{\bar {m}}}} \right)}^{2}} = \frac{{2{{N}_{0}}}}{N} - 3 + \frac{N}{{{{N}_{0}}}}\left[ {{{{\left( {\frac{{{{\sigma }_{0}}}}{{{{{\bar {m}}}_{0}}}}} \right)}}^{2}} + 1} \right].$$
(11)

Here, the subscript 0 denotes the flow of particles entering the apparatus. It follows from expression (11) that, with increasing particle coagulation probability (i.e., with decreasing number N of particles), the polydispersity of the coagulating system increases.

The presented examples demonstrate that Eq. (1) can be solved analytically when the change in the solid-phase particle distribution is mainly caused by either breakup, or coagulation. However, many processes are complicated by the simultaneous coagulation and breakup of solid-phase particles. Such a situation can occur, e.g., in a well-stirred continuous-flow granulator. In this case, Eq. (1) takes the form [8]

$$\frac{{\partial f(m,l,t)}}{{\partial t}} + w\frac{{\partial f(m,l,t)}}{{dz}} + f(m,l,t)\int\limits_0^\infty {k(m,s)f(s,l,t)ds} $$
$$\begin{gathered} + \;\frac{1}{2}f(m,l,t)\int\limits_0^m {g(m - s,s)ds} \\ = \frac{1}{2}\int\limits_0^m {k(m - s,s)f(m - s,l,t)f(s,l,t)ds} \\ \end{gathered} $$
(12)
$$ + \;\int\limits_m^\infty {g(s - m,m)f(s,l,t)ds} ,$$

where z is the longitudinal coordinate. Equation (12) should be complemented with expressions for the coagulation probability k(m, s) and breakup g(m − s, s). The expression for the probability of coagulation of two particles of masses m and s in un it time should take into account the fact that the formation of large particles is unlikely, whereas the collision of two very small particles in the presence of a sufficient amount of a binder almost certainly leads to their coalescence. Under this assumption, the kernel of the integral transform for coagulation can be approximated by the expression

$$k(m,s) = {{e}^{{ - B(m + s)}}}.$$
(13)

The coefficient B in this expression depends on the process conditions, including the binder content. The probability of breakup of a particle obviously increases with increasing its mass because of an increase in the number of inhomogeneities inside it, in the number of microcracks, local internal stresses, etc. Therefore, the kernel g(m − s, s) of the integral transform for breakup can be represented as

$$\begin{gathered} g(m - s,s) = s(m - s)(1-{{e}^{{-Cm}}}),\quad s < m, \\ g(m-s,s) = 0,\quad s > m. \\ \end{gathered} $$
(14)

The coefficients B and C for calculating the characteristics of a certain process can be found experimentally from the results of special tests.

Solving Eq. (12) for f(m, z, t) makes it possible to determine the dynamics of the change in the mass (size) of particles in the flow of the material being treated under the competition of coagulation and breakup. For a steady-state continuous process of change in the particle distribution, the explicit form of the dependence f(m, z) enables one to find the cross section of the apparatus in which the breakup begins to dominate the coagulation. For a well-stirred batch process, from the explicit form of the dependence f(m, t), it is easy to determine the time at which dynamic equilibrium between coagulation and breakup has been established. In this case, the derivative \(\frac{{\partial f(m,t)}}{{\partial t}}\) is zero, and Eq. (12) can be represented in the form

$$\begin{gathered} f(m) \\ = \frac{{\frac{1}{2}\int\limits_0^m {k(m - s,s)f(m - s)f(s)ds} + \int\limits_m^\infty {g(s - m,m)f(s)ds} }}{{\int\limits_0^\infty {k(m,s)f(s)ds + \frac{1}{2}\int\limits_0^m {g(m - s,s)ds} } }}, \\ \end{gathered} $$
(15)

which allows the use of the successive approximation method in finding the equilibrium function f(m). Solving this equation enables one to determine the final particle distribution in a batch process and its dependence on the process parameters.

This example of the use of Eq. (1) shows that it is an acceptable basis for analyzing processes involving simultaneous coagulation and breakup of particles. Approximations (13) and (14) can be used for probabilistic estimation of the coagulation and breakup of particles throughout the process. The dependence \(f(m)\) = \({{N}_{p}}(t){{A}^{2}}m{{e}^{{ - Am}}}\) is sufficiently flexible to fit accurately enough the actual dynamics of change in the particle distribution in a batch or continuous-flow apparatus, provided that the design of the apparatus ensures a near-plug flow of the material.

Of great practical interest is to model the continuous growth of large particles only due to small particles in the absence of coagulation or breakup of large particles. Such a case often takes place in granulation from solutions or deposition of coatings on particles. Then, the right-hand side of Eq. (1) is zero, and to describe such a process, this equation takes the form

$$\frac{{\partial f}}{{\partial t}} + \operatorname{div} (\bar {w} - {{D}_{p}}\vec {\nabla })f + \frac{\partial }{{\partial m}}\left( {u - \frac{\partial }{{\partial m}}{{D}_{m}}} \right)f = 0.$$
(16)

For apparatuses with well-stirred solid phase, this equation includes the mean residence time T of particles in the working space:

$$\frac{{\partial f}}{{\partial t}} + \frac{1}{T}f + \frac{\partial }{{\partial m}}uf = \frac{1}{T}{{f}_{0}}(m,t) + \frac{{{{\partial }^{2}}}}{{\partial {{m}^{2}}}}{{D}_{m}}F.$$
(17)

Under steady state process conditions, Eq. (17) has the exact solution

$$f(m) = \frac{1}{{Tu(m)}}\int\limits_{{{m}_{0}}}^m {{{f}_{0}}} (\zeta )\exp \left( { - \int\limits_\zeta ^m {\frac{{d\eta }}{{Tu(\eta )}}} } \right)d\zeta ,$$
(18)

which is valid if the diffusion in the mass space can be ignored, i.e., if the particle growth rate can be considered to be constant. One can show that this is so if the condition \(Tu \gg {{m}_{0}}\) is met, where m0 is the mass of a small particle.

In conclusion, we emphasize that mathematical modeling of the change in the solid-phase particle distribution based on integro-differential equation (1) seems to be efficient for a wide range of processes in which a change in the particle size affects noticeably the process intensity. The adequacy of the obtained solutions in all the considered cases was confirmed experimentally [4, 8].