INTRODUCTION

Over the past several decades, combustion over the surface of combustible materials have been investigated in numerous experimental and theoretical studies. Experiments have been carried out mainly on samples of some practically important materials such as wood [1, 2], paper [3], polymers [4, 5], polymethyl methacrylate (PMMA)[6–8] or in pools with combustible liquids [9, 10].

For these systems, many experimental studies have been performed and various models of the phenomenon have been proposed [11–22]. However, many fundamental issues for constructing such models still remain unclear. These include the choice of the main heat transfer mechanism during flame spread over the surface of a liquid. In experiments performed to determine the dominant mechanism of heat transfer, conflicting results have been obtained. Heat flow measurements using holographic interferometry have shown that in any regime of flame spread over the PMMA surface, heat transfer in the gas phase is dominant [6, 7]. However, it has been found [5, 8] that heat transfer in the condensed phase cannot be neglected.

In [15], it was first proposed to divide the investigated systems into thermally thick and thermally thin systems. These limiting cases are mathematically described in different ways. Subsequently, many researchers began to use the terms thermally thin and thermally thick for the fuel layer; however, criteria for the applicability of these terms are not always given. Analysis of these criteria as applied to the flame spread process is presented in [19] and [23]. The thermal thinness criterion is expressed as follows: the characteristic time of thermal relaxation of a fuel layer in the direction perpendicular to the direction of flame spread (\(\tau _{\bot}=h^{2}/\varkappa _{ \bot })\) must be shorter than the characteristic time of heat transfer along the substrate (\(\tau _{ \Uparrow }=\varkappa _{ \Uparrow }/u^{2})\) in the direction of flame spread. Here \(h\) is the thickness of the fuel layer, \(\varkappa\) is the thermal diffusivity, and \(u\) is the combustion wave velocity.

Analysis of the thermal thinness criterion as applied to particular experimental conditions, as a rule, has not been carried out. Our analysis of the investigated substances has shown that PMMA and paper are not thermally thin regardless of their thickness. For example, it follows from experimental data [19] that in the entire range of thicknesses, the fuel layer is not thermally thin, \(0.9<\tau _{ \bot}/\tau _{ \Uparrow }<10^{3}\), i.e., the ratio for the characteristic times is inverse in most of the range.

Early studies have shown that the velocity of flame spread depends on both the kinetic characteristics of the gas-phase reaction and the thermophysical and geometric characteristics of the condensed phase. It is difficult to independently vary these characteristics by changing the combustible material. Therefore, to expand methodological capabilities and, in particular, to separately study the influence of the thermophysical properties of the system and the reactivity of fuels, a new model system—a liquid film fuel on a thin metal substrate—was chosen. By choosing the thickness of the metal substrate, it is easy to create a system that meets the thermal thinness conditions. Such systems can be considered to some extent as model systems for studying flame spread over the surface of various combustible materials (wood, plastic, etc.). Flame spread over natural materials is complicated by the fact that the gas-phase combustion reaction is usually accompanied by various physicochemical processes involving conversions of combustible material, such as pyrolysis, gasification, phase transitions, heterogeneous reactions, etc. It is practically impossible to vary the individual parameters of a combustible system for research purposes while keeping other parameters constant.

The goal of studying the combustion of liquid fuels on substrates has been to identify flame spread regimes in a model system of a liquid fuel film on a metal substrate and the limited set of substrate and fuel parameters responsible for the occurrence of a particular regime by independently varying the thermophysical and geometric properties of the substrate not involved in chemical reaction, (thermal conductivity, specific heat capacity, density, thickness) and the properties of liquid fuels (the surface tension coefficient and its dependence on temperature, viscosity, heat of evaporation, boiling point, chemical nature).

This goal has been achieved by varying the parameters of the substrate, fuel, and the geometry of the samples and their orientation relative to the acceleration vector due to gravity. As a result of experimental studies, a number of steady and unsteady regimes have been identified.

Among these, the free-convective and low-velocity flame spread regimes can be distinguished based on the spread mechanism. In the free convective regime, the flame spreads upward. The rising combustion products heat the fuel film, which evaporates and burns to form a new portion of combustion products. The flame spread velocity in this case depends on the angle of inclination of the substrate to the horizon, weakly depends on the properties of the fuels C10H22–C16H34( saturated hydrocarbons with 10 to 16 atoms), and reaches maximum values of about 30 cm/s in the case of a vertical position of the substrate [24, 25].

In the low-velocity regime, the flame velocity over the fuel on thermally thin substrates is about 2 cm/s. For the system of a fuel film on a high-thermal-conductivity substrate, it has been shown that the basic mechanism of flame spread is forward heat transfer through the substrate from the combustion products to the cold preflame zone with the fuel film. A mathematical model for this flame spread mechanism is proposed in [26]. It has also been shown experimentally that for copper substrates, the heat flow under the action of capillary forces caused by the temperature gradient along the substrate (Marangoni effect) can be neglected.

Diffusion combustion over a liquid fuel film on a high-thermal-conductivity substrate is considered in [27] using the Burke–Schumann model. The length and shape of the flame were calculated theoretically and shown to agree well with experimental data. Experiments [28] were carried out with a thin copper substrate using opposed air flow or air enriched in methane in order to increase the flame spread velocity and shift the velocity limit of the oxidizer flow. Saturated hydrocarbons with more than nine carbon atoms were used as fuels. New experimental evidence was obtained for the efficiency of the estimate proposed in [26] for the flame velocity in a thermally thin system. In addition, it was first shown experimentally that the flame velocity does not depend on the velocity of the opposed flow of air or a methane–air mixture. However, the hypothesis proposed in [28] for the flame spread limit in this system is consistent with experiment only if the fuel film flow is taken into account. It has been shown [29] that the flame spread velocity does not depend on the thickness of the fuel film when it is greater than 3 \(\mu\)m. It has been found that melting of the fuel film does not affect the flame spread velocity. In this study [29], devoted mainly to the effect of the initial temperature on the velocity of flame spread over the liquid fuel film on metal substrates, it has also been shown that the model proposed in [26] for calculating the flame velocity is in satisfactory agreement with experiment, but the flame spread limit is due to the impossibility of providing sufficient thickness of the evaporating fuel film due to the Marangoni effect. Thus, various experiments indicate that under certain conditions, the Marangoni effect can have a significant effect on flame spread in thermally thin systems.

The objective of the present work is to determine the governing parameters of flame spread over a liquid fuel film on a low-thermal-conductivity substrate based on experimental data.

EXPERIMENT

The experiments were carried out with liquid fuels on thin substrates of polyethylene terephthalate (Mylar) and mica and on a thick (5 mm) layer of PMMA. In these experiments, in contrast to experiments on metal substrates with a fuel film, the fuel ahead of the flame cannot be heated by heat transfer in the substrate, which has the same low thermal diffusivity (for Mylar, 0.001 cm2/s, for mica, 0.025 parallel and 0.0028 cm2/s perpendicular to the plane [30], and for PMMA, 0.001 cm2/s) as the combustible liquid (0.0008 cm2/s). At room temperature, the typical flame spread velocities \(u\) over an n-butanol film on a mica substrate with a thickness \(h_{s}\) =12 \(\mu\)m are 3.1 to 3.3 cm/s for the flame spreading from one side of the substrate, and 5.6 cm/s for the flame spreading from both sides. For a substrate thickness \(h_{s}\) = 24 \(\mu\)m, the flame velocity is \(u\) = 1.9 cm/s in the case of one-sided flame and \(u\) = 3.5 cm/s for two-sided flame. When using 2-butanol as fuel, the characteristic rate of flame spread on thin substrates of polyethylene terephthalate (Mylar) is about 2.6 cm/s with a standard deviation of \(\pm \)0.4 cm/s. On a thick PMMA substrate, we have \(u\) = 1.7 cm/s.

The experiment with thin substrates was performed as follows. A fuel film was applied to the substrate, and flame was initiated with an open fire. The substrate was a strip of polyethylene terephthalate 10 cm wide, 50–100 cm long, and 50 \(\mu\)m thick. The alcohols n-butanol and 2-butanol were used as fuel. The substrate was positioned in space vertically, horizontally or under an angle to the gravity vector. As a result of downward flame spread on a vertical substrate, polyethylene terephthalate melted and burned. Therefore, the fuel was applied, not to the entire width of the substrate, but as a strip 5–6 cm wide, and the edges 2.5–2 cm wide remained dry and did not melt during combustion, thus maintaining the substrate position in space.

Two types of experiments were performed. In the first experimental setup, fluorescent dye rhodamine 6G was added to the liquid fuel, and the liquid film was illuminated by a semiconductor laser light with a wavelength of 532 nm, corresponding to the absorption of this dye. The flame spread was video-recorded, and video recordings were used to calculate the flame velocity. An increase in the fluorescence intensity corresponded to an increase in the thickness of the liquid film due to the motion of the liquid. This zone of increased fluorescence was observed directly ahead of and under the leading edge of the flame, and its width was \(\delta \) = 1 mm. Behind the leading edge of the flame, an evaporating fuel film about 1 cm long was observed along the coordinate of flame spread. These experiments were performed on a vertical substrate with downward flame spread.

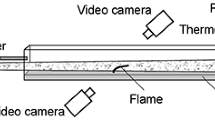
The experimental setup for the second type of experiments is similar to that presented in [31] and shown in Fig. 1. A photodiode was attached to one end of the narrow tube, and the second open end of the tube was located at a height of 1 cm from the substrate surface exactly opposite the thermocouple located on the back side of the substrate. The substrate was positioned horizontally. The temperature of the substrate and the self-luminescence of the flame were measured simultaneously. The measurements were carried out with a copper–Constantan thermocouple 100 \(\mu\)m thick.

Fig. 1
figure 1

Diagram of flame spread: ( 1) substrate; ( 2) fuel film; ( 3) flame front; ( 4) photodiode in a narrow channel; ( 5) thermocouple.

Full size image
Fig. 2
figure 2

Time dependences of the substrate temperature ( 1) and flame luminescence intensity ( 2); curve 3 shows the temperature \(T_{v}\) corresponding to the stoichiometric fuel vapor concentration; flame velocity 2.1 cm/s.

Full size image

Figure 2 shows typical time dependences of the temperature during flame spread (curve 1) and flame self-luminescence (curve 2). In this case, 2-butanol fuel was used and the flame velocity was 2.1 cm/s.

DISCUSSION

Using the experimental data, we estimate the characteristic rates of the processes accompanying flame spread over a fuel film on a substrate.

We first estimate the characteristic time of heat transfer processes. For a fuel film with an initial thickness \(h_{f}\) = 10 \(\mu\)m, the characteristic heating time is \(\tau _f~=~{h_f^2 }/{k_f } \approx 0.001\) s. The characteristic heating time of the substrate is \(\tau _s = {h_s^2 }/{k_s } \approx 0.025\) s. The characteristic residence time of the fuel in the zone of increased thickness of the liquid film ahead of the flame front is \(\tau _\delta = {\delta }/{u} \approx 0.05\) s. It can be seen that during this time, the fuel film of the initial thickness can be heated and the heating of the substrate will be delayed. That is, the fuel film will have the same temperature in the direction normal to the substrate surface and the substrate will not. However, since the substrate is sufficiently thin, its heat capacity is low and the substrate is also heated. Generally, however, the substrate–fuel system is not thermally thin.

Experiments on a vertical substrate with the addition of the dye showed marked differences in the behavior of the liquid fuel film on the low-thermal-conductivity substrate compared to the copper substrate. The size of the region with an increased thickness of the liquid film ahead of the edge of the flame front \(\delta \approx 0.1\) cm is much smaller than the size of the similar region on the high-thermal-conductivity substrate, where it is 1–1.5 cm [31]. Moreover, on low-thermal-conductivity vertical substrates during downward flame spread, there is no fuel flow from this region ahead of the flame front that is characteristic of spread over high-thermal-conductivity substrates [31]. The length of the evaporating fuel region under the flame front is about 1 cm, which is of the same order as on high-thermal-conductivity substrates, where this parameter is equal to 0.1–1 cm, depending on the type of fuel [31].

On metal substrates, the size of the heated substrate region ahead of the flame front \(\delta \) \(_{m}\) is determined by the thermal diffusivity \(\varkappa\)of the substrate–fuel system [31] and the flame velocity \(u\):

$$\delta _{m} =\varkappa /u,$$
$$\varkappa = \frac{\lambda _s h_s + \lambda _f h_f }{c_s \rho _s h_s + c_f \rho_{fs} h_f } \approx \frac{\lambda _s h_s }{c_s \rho _s h_s + c_f \rho _{fs}h_f }.$$

Here \(\lambda \), \(c\), \(\rho \), and \(h\) are the thermal conductivity, specific heat, density, and thickness of the layer (the subscripts \(s\) and \(f\) refer to the substrate and fuel, respectively). For example, for substrates made of steel and copper, \(\varkappa _{s}\approx 0.2\) and 1 cm2/s, respectively, and for paper and polymer samples, \(\varkappa _{s}\approx 10^{ - 3}\) cm2/s. Therefore, systems with metal substrates can be characterized by wide heating zones. Indeed, for the investigated samples, the numerical estimate is \(\varkappa /u\approx 0.1-1\) cm, which agrees with the experiment. For conductive heat transfer in the solid and liquid phases for the system under study at \(u\) = 2 cm/s, similar estimates of possible heating zones are \(\varkappa /u\sim 10^{ - 3}\) and 10\(^{-4}\) cm, respectively. However, the observed size\(\delta \)is much larger, of the order of 0.1 cm, which is close to the values for metal substrates.

Consider what is the reason for the increase in the thickness of the fuel film ahead of the flame edge. We will assume, according to [26, 32], that under the leading edge of the flame, the temperature of the liquid fuel \(T_{v}\) is equal to the temperature at which the vapor pressure corresponds to a stoichiometric mixture with air. Here \(T_v \) = 304.44 K = 31.3°C is the temperature at which the equilibrium vapor pressure of 2-butanol in air creates a stoichiometric mixture with a volume fraction of 0.0338. The temperature dependence of the vapor pressure for 2-butanol is taken from [33] in the form \(\log p = A - {B}/({T + C})\), where \(A\) = 4.546, \(B\) = 1351.55, and \(C\) = 93.34 (the pressure is in bar, and the temperature is in Kelvin).

If the fuel film were solid and not liquid, then, neglecting heat exchange with the gas phase, in the heating zone, as on metal substrates, one would expect, as in [32], the following dependence of temperature on the coordinate \(x\) along the direction of flame spread:

$$T = ( {T_v - T_0 } )\exp ({ux}/{\varkappa }).$$

At \(x\) = 0, near the flame edge, the temperature gradient \(\displaystyle\frac{dT}{dx}~=~({T_v - T_0 } )\frac{u}{\varkappa _f } = 3.3 \cdot 10^4\) K/cm. However, since our film is not solid but liquid, then such a gradient would cause the fluid to move [26] with an average velocity

$$ v = \frac{h_f }{2\mu }\,\sigma _T \frac{dT}{dx} \approx 0.35\ \textrm{m/s}.$$
(1)

The temperature dependence of the surface tension coefficient \(\sigma \)in this temperature range is linear, \(\displaystyle\sigma _{T}~=~\frac{d\sigma}{dT}=0.85 \,\cdot\, 10^{ - 4}\) N/(m\(\ \,\cdot\, \)K) [33]; the temperature dependence of the dynamic viscosity of the liquid fuel\(\mu \) is nonlinear and varies from 3\(\ \,\cdot\, \)10\(^{ - 3}\) to 0.54\(\ \,\cdot\, \)10\(^{ - 3}\) Pa\(\ \,\cdot\, \)s in the temperature range 20–100°C. This motion would lead to heat transfer due to the forward motion of the liquid and to a decrease in the temperature gradient and the velocity of the fuel film. Apparently, this gives rise to a temperature gradient which provides steady motion of liquid fuel rim ahead of the flame edge.

The motion of the film ahead of the flame edge causes it to thicken. Consider what can be the thickness of the fuel film ahead of the flame edge on the vertically positioned substrate. No liquid fuel flow from the thickening indicates that the average velocity of the fuel film flow \(w_{m}\) is lower than the flame velocity. For the liquid layer at distance \(y\) from the vertical substrate, the velocity \(w\) will be constant for the equality of the gravity and friction forces:

$$\rho g + \mu \frac{d^2w}{dy^2} = 0.$$

The boundary conditions for this equation will be \(w\) = 0 at \(y\) = 0 and \(\displaystyle\frac{dw}{dy} =0\) at \(y=h_{f}\). The solution of this equation is the dependence of the velocity of the fuel film flow on the coordinate \(\displaystyle w = \frac{\rho g}{\mu }\,y\bigg( {h_f -\frac{y}{2}} \bigg)\). Averaging over the fuel film thickness yields the relation \(\displaystyle w_m~=~\frac{\rho g}{\mu }\frac{h_f^2}{3}\). Thus, outflow is possible if the thickness of the fuel film in the thickening is greater than \(\displaystyle \sqrt {\frac{3\mu u}{\rho g}} = 0.155 \cdot 10^{ - 3}\) m = 155 \(\mu\)m. This is the upper estimate of the fuel film thickness near the flame edge. The temperature gradient ahead of the flame edge can be estimated as \(\displaystyle \frac{dT}{dx} = \frac{T_v - T_0 }{\delta } \approx 153\) K/cm. With this thickness, the fuel film should move under the action of capillary forces [Eq. (1)] with the average velocity

$$v = \frac{\sigma _T h_f }{2\mu }\frac{dT}{dx} \approx 0.046\textrm{~m/s},$$

This velocity value is higher than the experimental value \(u\) = 0.021 m/s. That is, with such a thickness, the fuel film would flow out from under the edge of the flame. This indicates that the film thickness under the flame is less than 155 \(\mu\)m.

Thus, the results of experiments with the dye on vertical substrates indicate that the thickness of the film burning per unit time is equal to the initial thickness \(h_{f0}\) (no outflow), and the thickness of the film under the flame edge is in the range \(h_{f0}<h_{f} <155\) \(\mu\)m.

Consider Fig. 2 in more detail. Unlike in [31], the thermocouple signal does not advance the photodiode signal, which may be due to two reasons. The first is the inertia of thermocouples. The second reason is that the substrate–fuel system has a low thermal diffusivity and, therefore, the temperature determined from the signal of the thermocouple on the side of the substrate opposite to the flame at a given time is lower than that on the fuel surface. Both reasons lead to an underestimation of the temperature on the bottom side of the substrate compared to the top side.

Nevertheless, we estimate the temperature gradient and the liquid velocity near the flame edge based on the experimental data presented in Fig. 2. It is obvious that under the flame front, the liquid is heated due to the thermal conductivity of the gas. Since the liquid portion under the flame that is farther from the flame leading edge is heated longer and to a higher temperature than the portion that has just entered the flame. This creates a temperature gradient in the liquid along the direction of motion of the flame. Thus, due to the Marangoni effect, the liquid with a high surface temperature and the adjacent gas with high liquid vapor density move in the direction of flame motion to the cold region. Using the data presented in Fig. 2, it is possible to calculate the temperature gradient at \(T_{v}\) = 31.3°C. Experimental data on the time dependence of the temperature near \(T_{v}\) were approximated by a polynomial of the second degree; it was differentiated with respect to time and the result was divided by the flame spread velocity. The temperature gradient obtained in this way is 65 K/cm, which is more than half the estimated gradient ahead of the flame edge (153 K/cm). This is not surprising since the signal of the thermocouple on the back side of the substrate is delayed compared to the top surface of the fuel.

It has been shown [29] that the flow velocity of the top layer of liquid fuel is always higher than the flame spread velocity. No fuel flow from the rim indicates that the effective thickness of the burning fuel film \(h_\mathrm{ eff}\) is equal to the original thickness \(h_\mathrm{ eff}=h_{f0}\) = 10 \(\mu\)m, and the thickness of the film under the flame edge can be estimated through the temperature gradient near \(T_{v}\). According to [29], the expression for \(h_\mathrm{ eff}\) has the form

$$ h_\mathrm{ eff} \rho _f u = h_f \rho _f u - \frac{h_f^2 \rho _f \sigma _T }{2\mu }\frac{dT}{dx}.$$
(2)

Here, the first term on the right-hand side expresses the fuel mass per unit cross-sectional area of the film that flows under the edge of the flame moving with velocity \(u\), and the second term is the amount of fuel that escapes from under the flame front forward into the colder region. It follows from (2) that the thickness of the fuel film under the flame edge can have two values. It has been shown [29] that steady flame spread is possible only for the larger value of \(h_{f}\):

$$h_f = {\mu u}\bigg/\bigg(\sigma _T \frac{dT}{dx}\bigg){}$$
$${}\times\bigg[1 + \sqrt {1 -h_{f0}\bigg(2\sigma _T \frac{dT}{dx}\bigg)\bigg/({\mu u}) }\bigg] {}$$
$${}\approx 6 \cdot 10^{ - 5}\textrm{~m} = 60~\mu\textrm{m}.$$

In this calculation, a temperature gradient of 153 K/cm is assumed; at a gradient of 65 K/cm, the thickness of the film would be 156 \(\mu\)m and, according to the above estimates, the film would flow out of the thickening.

At a temperature gradient of 153 K/cm, a film 60 \(\mu\)m thick would move under the action of capillary forces with the average velocity [Eq. (1)]

$$v = \frac{\sigma _T h_f }{2\mu }\frac{dT}{dx} \approx 0.018\textrm{~m/s},$$

and at a temperature gradient of 65 K/cm, a film 156 \(\mu\)m thick would move under the action of capillary forces with an average velocity of 0.02 m/s. These estimates give values close to the flame velocity. In this case, the velocity of the film on the surface will be twice as high.

The above estimates of the characteristic heating time of the fuel were carried out for the initial fuel film thickness. If, however, the thickness of the film under the leading edge of the flame is taken equal to 60 \(\mu\)m, the characteristic heating time, e.g., for \(h_{f}\) = 60 \(\mu\)m, will be \(\tau _{f}\) = 0.045 s. This quantity is of the same order as \(\tau _{\delta}\) = 0.05 s. That is, the liquid fuel layer with this thickness is not thermally thin.

We estimate the velocity \(v\) of the diffusion fuel flow in the gas phase near the flame edge, where the fuel temperature is \(T_{v}\). Diffusion occurs along the direction of flame spread and in the perpendicular direction. We are interested in the rate of diffusion to the flame edge along the direction of spread:

$$ v = \frac{D}{\rho _g }\frac{\partial c_f }{\partial x}.$$
(3)

Here \(\rho _g \) is the density of the gas mixture, and the fuel concentration gradient can be represented as

$$\frac{\partial c_f }{\partial x} = \frac{\partial \rho _f }{\partial x} = \frac{M}{R}\frac{\partial ( {p}/{T})}{\partial x} {}$$
$${}=\frac{M}{R}\bigg[ {\frac{\partial p}{T\partial x} - \frac{p}{T^2}\frac{\partial T}{\partial x}} \bigg] {}$$
$$ =\frac{Mp}{RT}\bigg[ {\ln (10)\frac{B}{( {T + C} )^2} - \frac{1}{T}}\bigg]\frac{\partial T}{\partial x}$$
(4)

(\(M\) is the molecular weight of the fuel and \(R\) is the universal gas constant). Substitution of the numerical values of the corresponding quantities into Eq. (4) yields

$$\frac{\partial c_f }{\partial x} = 8.6 \cdot 10^3\textrm{~kg/m}^{4}$$

at a temperature gradient of 65 K/cm. Substituting the calculated concentration gradient into Eq. (3) and using \(D\) = 0.085\(\,\cdot\, \)10\(^{ - 4}\) m2/s at 300 K [33] and \(\rho\) \(_{g}\) = 1 kg/m\(^{3}\), we obtain the following estimates for the diffusion rate: \(v\) = 0.073 m/s at a temperature gradient of 65 K/cm and \(v\) = 0.17 m/s at 153 K/cm. It should be noted that this is an estimate of the diffusion rate with respect to the moving fuel film, and the top layer of the fuel film also moves to the flame edge with a velocity twice the average velocity of the film.

CONCLUSIONS

The flame spread velocity is determined by the temperature gradient of the liquid near the leading edge of the flame.

The temperature gradient is determined not only by the thermophysical properties of the fuel and the substrate and their thicknesses, but mainly by the dependence of the surface tension coefficient on the temperature and dynamic viscosity of the liquid fuel. The role of the substrate reduces to heat loss, which is determined by the heat capacity and thickness of the substrate. Thus, the determining mechanism of heat transfer through the condensed phase is the motion of the liquid due to the Marangoni effect.

The temperature gradient along the surface of the liquid film determines the velocity of film motion and the rate of diffusion of the evaporated fuel to the flame edge.