INTRODUCTION

Forest fires have a powerful impact on global environmental changes. Traces of this disastrous events can be found on every continent. Among recent events are fires in the central and northern parts of Portugal and Spain (October 2017); in East Attica (Greece), where whole villages burned to the ground and many casualties occurred (July, 2018); wildfire in upstate California, the most destructive and deadly in the history of the state (November, 2018); in Russia, natural fires occur annually, causing huge economic and social damage [1].

Complex phenomena such as forest fires are studied using physical and mathematical modeling. Mathematical modeling has a number of advantages over physical experiments, e.g., environmental safety and greater economic efficiency. Mathematical modeling of crown forest fires was carried out in [2–6]. In [2], a mathematical model was proposed that takes into account the main physicochemical processes occurring in a forest fire. In that work, in addition to a consideration of the general dynamics of fire behavior, the effect of fire barriers on forest fire spread was analyzed. The model made it possible to evaluate the geometry of the fire front and the velocity of crown forest fire spread.

Fire breaks and barriers are used to ensure optimal fire safety in forests, prevent ignitions and fires, and suppress fire spread in selected regions. Creating a system of fire barriers and maintaining its good operating condition requires considerable cost. Therefore, it should be scientifically sound and effective. Although the creation of fire barriers has been the subject of many studies, this problem has been insufficiently studied. In [7], the results of experiments and mathematical modeling were used to propose parameters of fire barriers in a pine forest; however, this is insufficient due to the great diversity of forest vegetation. The principles of creating fire forest barriers from deciduous species for prevention of crown fires were considered in [8]. Based on the results a of field investigation of the consequences of the catastrophic crown fires in the island forest-steppe forests of the Kurgan region in 2004, which propagated through a zone of 50–70-year-old birch stand of medium density, it has been proposed to create deciduous fire breaks at least 150 m wide. A disadvantage of papers [7, 8] is that they provide a limited description of the process, which is typical of many semi-empirical and experimental studies. A consistent physical model of forest fire is not available, and physicochemical processes in forest fire zones are not considered. Mention should be made of a numerical simulation study [9] of the spread of ground forest fires taking into account a fire break. However, since the intensity of a ground fire is lower than that of a crown fire, the parameters obtained in [9] cannot be used to estimate the parameters of the latter.

The aim of this work was to study the fundamental physical mechanisms of the initiation and propagation of combustion in crown forest fires. The problem of increasing the effectiveness of fire barriers and controlling their protective effect is also considered.

PHYSICAL FORMULATION OF THE PROBLEM

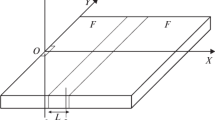
Let the ignition source have finite sizes, and let the coordinate origin be associated with the center of the source. The \(OZ\) axis is directed vertically up, and the \(OX\) and \(OY\) axes are parallel to the Earth’s surface. The \(OX\) axis coincides with the wind direction. Under the action of the wind, the forest fire source begins to spread through the forest. Figure 1 schematically shows the region including the forest and the fire barrier or break of finite size.

MATHEMATICAL FORMULATION OF THE PROBLEM AND SOLUTION METHOD

The system of equations with boundary and initial conditions is derived using the following assumptions: (1)  the forest is a multi-phase, multi-component porous-dispersed medium; (2)  a two-temperature (different temperatures of the gas and condensed phases), single-velocity reactive medium is considered; (3)  the forest canopy is assumed to be non-deformable, and the resistance force of the forest canopy is represented in the equation of conservation of momentum in the gas phase, i.e., the medium is considered quasi-solid (almost non-deformable under wind gusts); (4)  a so-called ventilated forest is considered, in which the volume fraction of the condensed phase, consisting of dry organic matter, liquid water droplets, solid pyrolysis products and ash, can be neglected compared to the volume fraction of the gas phase (components of air and gaseous products of pyrolysis and combustion); (5)  the flow in the investigated region has a developed turbulent character; (6)  the density of the gaseous phase is independent of pressure due to the low flow velocity compared to the sound velocity.

Fig. 1
figure 1

Diagram of the fire zone: (1) ignition source; (2) fire barrier or break of finite size; \(F\) is a pine forest, and \(L_{x}\) and \(L_{y }\) are the sizes of the barriers along the \(OX\) and \(OY\) axes, respectively.

Full size image

Since the vertical sizes of a forest area are incomparably smaller than its horizontal sizes, the general system of differential equations of heat and mass transfer in a three-dimensional area can be integrated over the height of the forest canopy \(h\). For this, the original system of equations is reduced to divergent form and then integrated over the height of the forest canopy:

$$\displaystyle\int\limits_0^h {{\phi} dz} = \bar{\phi} h$$

(\(\bar{\phi}\) is the average value of \(\phi\) [3]).

To determine the source terms characterizing the inflow (outflow of mass) in a unit volume of the gas-dispersed phase, we used formulas for the rate of formation of the gas-dispersed phase \(\dot{m}\), oxygen consumption \(R_{51}\), and the change in the concentration of carbon monoxide \(R_{52}\). As a result, the mathematical problem reduces to solving the following system of equations:

$$\frac{\partial \rho }{\partial t} + \frac{\partial }{\partial x}\,( {\rho u} ) + \frac{\partial }{\partial y}\,( {\rho v} ) = \dot {m} - \frac{\dot {c}^ - - \dot {c}^ + }{h};$$
(1)
$$\rho \frac{du}{dt} = - \frac{\partial p}{\partial x} + \frac{\partial }{\partial x}\,( { - \rho \overline {u^{'2}} } ) + \frac{\partial }{\partial y}\,( { - \rho \overline {u'v'} } ) {}$$
$${}-\rho sc_d u| \vec {u} | - \dot {m}u + \frac{ {\tau _x^ - - \tau _x^ + } }{h};$$
(2)
$$\rho \frac{dv}{dt} = - \frac{\partial p}{\partial y} + \frac{\partial }{\partial x}\,( { - \rho \overline {u'v'} } ) + \frac{\partial }{\partial y}\,( { - \rho \overline {v^{'2}} } ) {}$$
$${}-\rho sc_d v| \vec {u} | - \dot {m}v + \frac{ {\tau _y^ - - \tau _y^ + } }{h};$$
(3)
$$\rho c_p \frac{dT}{dt} = \frac{\partial }{\partial x}\,( { - \rho c_p u'\overline {T'} } ) + \frac{\partial }{\partial y}\,( { - \rho c_p v'\overline {T'} } ) {}$$
$${}+q_5 R_5 - \alpha _v ( {T - T_s } ) {}$$
$${}+\frac{ {q_T^ - - q_T^ + } }{h} + k_g ( {cU_R - 4\sigma T^4} );$$
(4)
$$\rho \frac{dc_\alpha }{dt} = \frac{\partial }{\partial x}\,( - \rho \overline {u'c_\alpha ' } ) + \frac{\partial }{\partial y}\,( { - \rho \overline {v'c_\alpha ' } } ) {}$$
$${}+R_{5\alpha } - \dot {m}c_\alpha + \frac{ {J_\alpha ^ - - J_\alpha ^ + } }{h},\; \alpha =\overline {1,\,2};$$
(5)
$$\frac{\partial }{\partial x}\,\bigg( {\frac{c}{3k}\frac{\partial U_R }{\partial x}} \bigg) + \frac{\partial }{\partial y}\,\bigg( {\frac{c}{3k}\frac{\partial U_R }{\partial y}} \bigg) - kcU_R {}$$
$${}+4k_g \sigma T^4 + 4k_s \sigma T_s^4 = 0,\; k = k_g + k_s ;$$
(6)
$$\sum\limits_{i = 1}^4 \rho _i \varphi _i c_{pi} \frac{\partial T_s }{\partial t} = q_3 R_3 - q_2 R_2 {}$$
$${}+k_s ( {cU_R - 4\sigma T_s^4 } ) + \alpha _v ( {T - T_s } );$$
(7)
$$\rho _1 \frac{\partial \varphi _1 }{\partial t} = - R_1 ,\;\; \rho _2 \frac{\partial \varphi _2 }{\partial t} = - R_2 ,$$
(8)
$$\rho _3 \frac{\partial \varphi _3 }{\partial t} = \alpha _c R_1 - \frac{M_{C}}{M_1 }R_3 ,\;\; \rho _4 \frac{\partial \varphi _4 }{\partial t} = 0;\;\;$$
$$\sum\limits_{\alpha = 1}^3 {c_\alpha } = 1,\;\;\; p_e = \rho RT\sum\limits_{\alpha = 1}^3 {\frac{c_\alpha }{M_\alpha }},$$
$$\dot {m} = ( {1 - \alpha _c } )R_1 + R_2 + \frac{M_{C} }{M_1 }R_3,$$
(9)
$$R_{51} = - R_3 - \frac{M_1 }{2M_2 }R_5 ;\;\;\; R_{52} = v_g (1 - \alpha _c )R_1 - R_5.$$
Fig. 2
figure 2

Distributions of gas-phase temperature (a and d) and concentrations of oxygen (b and e) and volatile pyrolysis products (c and f) for fire-break sizes of 20 \(\times\)30 m (a–c) and 20 \(\times\)50 m (d–f) at times \(t\) = 12.3 (I), 22 (II), and 25.1 s (III).

Full size image
Fig. 3
figure 3

Distributions of gas-phase temperature (a and d) and concentrations of oxygen (b and e) and volatile pyrolysis products (c and f) for fire-break sizes of 20 \(\times\)20 m (a–c) and 20 \(\times\)30 m (d–f) at times \(t\) = 7 (I), 12 (II), and 17 s (III).

Full size image
Fig. 4
figure 4

Distributions of gas-phase temperature (a and d) and concentrations of oxygen (b and e) and volatile pyrolysis products (c and f) for fire-break sizes of 20 \(\times\)20 m (a–c) and 20 \(\times\)30 m (d–f) at times \(t\) = 7.5 (I), 12 (II), and 14 s (III).

Full size image
Fig. 5
figure 5

Distributions of gas-phase temperature (a and d) and concentrations of oxygen (b and e) and volatile pyrolysis products (c and f) for fire-break sizes of 20 \(\times\)10 m (a–c) and 20 \(\times\)20 m (d–f) at times \(t\) = 6 (I), 10 (II), and 12 s (III).

Full size image
Fig. 6
figure 6

Break size \(L_{y}\) versus wind velocity \(v_e\).

Full size image
Fig. 7
figure 7

Distributions of gas-phase temperature (a and d) and concentrations oxygen (b and e) and volatile pyrolysis products (c and f) for a fire-break size 40 \(\times\)40 m (a–c) and 40 \(\times\)50 m (d–f) at times \(t\) = 12 (I), 26 (II), and 29 s (III).

Full size image
Fig. 8
figure 8

Distributions of gas-phase temperature (a and d) and concentrations of oxygen (b and e) and volatile pyrolysis products (c and f) for fire-break sizes of 20 \(\times\)20 m (a–c) and 40 \(\times\)20 m (d–f) at times \(t\) = 7.5 (I), 19 (II), and 28 s (III).

Full size image
Fig. 9
figure 9

Distributions of gas-phase temperature (a and d) and concentrations of oxygen (b and e) and volatile pyrolysis products (c and f) for fire-barrier sizes of 20 \(\times\)20 m (a–c) and 40 \(\times\)20 m (d–f) at times \(t\) = 8 (I), 15 (II), 8.2 (III), and 16.5 s (IV).

Full size image
Fig. 10
figure 10

Distributions of gas-phase temperature (a and d) and concentrations of oxygen (b and e) and volatile pyrolysis products (c and f) for fire-break sizes of 40 \(\times\)40 m (a–c) and 40 \(\times\)60 m (d–f) at times \(t\) = 7 (I), 13.1 (II), and 15 s (III).

Full size image
Fig. 11
figure 11

Barrier size \(L_{y}\) versus wind velocity \(v_e\).

Full size image

Pyrolysis, moisture evaporation, and the combustion of condensed and volatile products of pyrolysis are described by the relations

$$R_1 = k_1 \rho _1 \varphi _1 \exp \bigg( { - \frac{E_1 }{RT_s }} \bigg),$$
$$R_2 = k_2 T^{ - 0.5}\rho _2 \varphi _2 \exp \bigg( { - \frac{E_2 }{RT_s }}\bigg),$$
(10)
$$R_3 = k_3 \rho s_\sigma \varphi _3 c_1 \exp \bigg( { - \frac{E_3 }{RT_s }}\bigg),$$
$$R_5 = k_5 M_2 \bigg( {\frac{c_1 M}{M_1 }} \bigg)^{0.25} \frac{c_2 M}{M_2}T^{ - 2.25}\exp \bigg( { - \frac{E_5 }{RT}} \bigg).$$

The above system of equations is solved subject to the following initial and boundary conditions:

$$t = 0{:}\quad u = 0,\;v = 0,\;T = T_e ,\;c_\alpha = c_{\alpha e} ,\;$$
$$T_s = T_e ,\;\varphi _i = \varphi _{ie} ;$$
(11)
$$x = 0{:}\quad u = V_e ,\;v = 0,\;T = T_e ,\;c_\alpha = c_{\alpha e} ,$$
$$-\frac{c}{3k}\frac{\partial U_R }{\partial x} + \frac{cU_R }{2} = 0;$$
(12)
$$x = x_e{:}\quad \frac{\partial u}{\partial x} = 0,\;\frac{\partial v}{\partial x} = 0,\;\frac{\partial c_\alpha }{\partial x} = 0,$$
$$\frac{\partial T}{\partial x} = 0,\; \frac{c}{3k}\frac{\partial U_R }{\partial x} + \frac{cU_R }{2} = 0;$$
(13)
$$y = 0{:}\quad \frac{\partial u}{\partial y} = 0,\; \frac{\partial v}{\partial y} = 0,\; \frac{\partial c_\alpha }{\partial y} = 0,$$
$$\frac{\partial T}{\partial y} =0,\; - \frac{c}{3k}\frac{\partial U_R }{\partial y} + \frac{cU_R }{2} = 0;$$
(14)
$$y = y_e{:}\quad \frac{\partial u}{\partial y} = 0,\; \frac{\partial v}{\partial y} = 0,\; \frac{\partial c_\alpha }{\partial y} = 0,$$
$$\frac{\partial T}{\partial y} = 0,\; \frac{c}{3k}\frac{\partial U_R }{\partial y} + \frac{cU_R }{2} = 0.$$
(15)

The coordinates of the ignition source are \(|x|\leqslant \delta_x\) and \(|y|\leqslant \delta_y\), where \(\delta_x\) and \(\delta_y\) are the sizes of the source along the \(OX\) and \(OY\) axes, respectively. The temperature in the ignition source varies with time:

$$T = T_s = \left\{ {\begin{array}{l} T_e + \displaystyle\frac{t}{t_0 }( {T_0 + T_e } ), t \le t_0, \\[4mm] T_e + (T_0 - T_e )\exp \bigg[ { - k\bigg( {\displaystyle\frac{t}{t_0 } - 1} \bigg)}\bigg], t > t_0. \end{array}} \right.$$

Assuming that heat and mass transfer in the fire front with the surface layer of the atmosphere and the lower storey of the forest obeys Newton’s law, the corresponding terms of the equations can be written as [3]

$$\frac{ {J_\alpha ^ - - J_\alpha ^ + }}{h} = - \frac{\alpha }{c_{ps} h}\,( {c_\alpha - c_{\alpha e} } ),$$
(16)
$$\frac{ {q_T^ - - q_T^ + } }{h} = - \frac{\alpha }{h}\,( {T -T_e } ).$$
(17)

The moisture content of forest fuel (FF) is a dimensionless quantity and is given by the formula \(W=(m-m_0)/m_0\), where \(m\) is the mass of FF in the natural state and \(m_{0}\) is the mass of FF in the absolutely dry state.

The following notation is used in the equations: \(R_{1}\mbox{--} R_{3}\) and \(R_{5\alpha }\) are the mass rates of FF pyrolysis, moisture evaporation, combustion of condensed and volatile pyrolysis products, soot and ash formation, and the formation of component \(\alpha\) of the gas-dispersed phase, \(t_{0}\) is the time of formation of the burning zone, \(c_{pi}\), \(\rho _{i}\), and \(\phi _{i}\) are the specific heat, true density, and volume fraction of the \(i\) th phase (\(i\) = 1 refers to dry organic matter, 2 to water in the liquid-droplet state, 3 to the condensed pyrolysis products, and 4 to the mineral component), \(\tau_i\), \(q_T\), and \(J_\alpha\) are the characteristics of momentum, energy, and mass exchange of component \(\alpha\) with both the surface layer of the atmosphere and the lower storey of the forest, \(T\) and \(T_{s}\) are the temperatures of the gas and condensed phases, \(c_{\alpha }\) is the mass concentration (subscript \(\alpha\) = 1 refers to oxygen, 2 to combustible pyrolysis products, and 3 to the inert components of air), \(p\) is the pressure, \(U_{R}\) is the radiation energy density, \(\sigma\) is the Stefan–Boltzmann constant, \(k\) is the radiation attenuation coefficient, \(k_{g}\) and \(k_{s}\) are the absorption coefficients for the gas-dispersed and condensed phases, \(\alpha _{v }\) is the phase exchange coefficient, \(q_{i}\), \(E_{i}\), and \(k_{i}\) are the heat, activation energy, and pre-exponential factor of the pyrolysis, evaporation, and combustion of coke and volatile pyrolysis products, \(s_{\sigma }\) is the specific surface of an FF element, \(M_{\alpha }\), \(M_{C}\), and \(M\) are the molecular weights of individual components of the gas phase, carbon, and air mixture, \(s\) and \(c_{d }\) are the specific surface area of phytomass and the empirical coefficient of resistance of the forest canopy, respectively, \(c\) is the speed of light, \(u\) and \(v\) are the projections of the velocity onto the \(X\) and \(Y\) axes, respectively, \(\alpha _c\) and \(\nu _c\) are the coke number and the mass fraction of combustible gases in the volatile products of pyrolysis, \(\dot{m}\) is the mass rate of formation of the gas-dispersed phase, and \(g\) is the acceleration due to gravity. The subscript 0 refers to the parameters in the burning zone, and subscript \(e\) to the parameters at a large distance from the fire zone [3]. The total derivative is

$$\frac{d}{dt}=\frac{\partial}{\partial t}+u\frac{\partial}{\partial x}+v\frac{\partial}{\partial y}.$$

The heat-transfer coefficient of the phases was selected on the basis of data on heat transfer between a FF element (needle and twig) and the surrounding medium \(\alpha\) using the formula

$$\alpha_V=\alpha S-\gamma c_p\dot{m},\;\; S=2\varphi_s/r_s,$$

where \(\gamma\) is the ratio of the molecular weights of the ambient gas and the gas released due to heat transfer, \(\varphi_s=\sum\limits_{i=1}^4\varphi_i\), and \(r_s\) is the radius of the cylinder (typical FF element) [3].

The turbulent fluxes of momentum, heat, and mass are written in terms of the mean flow gradients according to [6]:

$$\rho \overline{u'^2}=2\mu_t\frac{\partial u}{\partial x}-\frac{2}{3}\,K,$$
$$\rho \overline{v'^2}=2\mu_t\frac{\partial v}{\partial y}-\frac{2}{3}\,K,$$
$$-\rho \overline{u'v'}=\mu_t\bigg(\frac{\partial u}{\partial y}-\frac{\partial v}{\partial x}\bigg),\;\; \mu_t=\frac{c_{\mu}\rho K^2}{\varepsilon},$$
$$-\overline{\rho u'c_pT'}=\lambda_t\frac{\partial T}{\partial x},\;\; \lambda_t=\frac{\mu_tc_p}{\mbox{Pr}_t},$$
(18)
$$-\overline{\rho v'c_pT'}=\lambda_t\frac{\partial T}{\partial y},$$
$$-\overline{\rho u'c'_{\alpha}}=D_t\frac{\partial c_{\alpha}}{\partial x},\;\; \rho D_t=\frac{\mu_t}{\mbox{Sc}_t},$$
$$-\overline{\rho v'c'_{\alpha}}=D_t\frac{\partial c_{\alpha}}{\partial y}.$$

Here \(u'\) and \(v'\) are the pulsation velocity components in the projections onto the \(X\) and \(Y\) axes, respectively, and \(\mu_t\) is the turbulent dynamic viscosity determined using the locally equilibrium turbulence model [6]:

$$\mu_t=\rho l^2\bigg\{2\bigg[\bigg(\frac{\partial u}{\partial x}\bigg)^2+ \bigg(\frac{\partial v}{\partial y}\bigg)^2\bigg]{}$$
$${}+\bigg(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\bigg)^2- \frac{2}{3}\bigg(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\bigg)^2\bigg\}^{1/2};$$
(19)

\(\lambda_t\) and \(D_t\) are the thermal conductivity and turbulent diffusivity, \(c_{\mu}\) is a constant, \(\varepsilon\) is the dissipation rate of turbulent kinetic energy, \(K\) is the kinetic energy of turbulence, Pr\(_t\) and Sc\(_t\) are the turbulent Prandtl and Schmidt numbers, respectively, and \(l\) is the mixing path [10].

The characteristics of the forest correspond to the characteristics of the FF of a pine forest: \(E_{1}/R\) = 9400 K, \(k_{01}\) = 3.63\(\,\cdot\,\)10\(^{4 }\) s\(^{ - 1}\), \(E_{2}/R\) = 6000 K, \(k_{02}\) = 6\(\,\cdot\,\)10\(^{5}\) s\(^{ - 1}\), \(q_{2}\) = 3\(\,\cdot\,\)10\(^{6 }\) J/kg, \(E_{3}/R\) = 10 000 K, \(k_{03}\) = 10\(^{3}\) s\(^{ - 1}\), \(q_{3}\) = 1.2\(\,\cdot\,\)10\(^{7 }\) J/kg, \(E_{5}/R\) = 11 500 K, \(k_{5 }\) = 3\(\,\cdot\,\)10\(^{13}\) s\(^{ - 1}\), \(q_{5}\) = 10\(^{7 }\) J/kg, \(c_{p}\) = 1000 J/(kg\(\,\cdot\,\)K), \(\alpha _{c}\) = 0.06, \(\nu _{c}\) = 0.7, \(\rho _{e}\) = 1.2 kg/m\(^{3}\), \(c_{2e}\) = 0, \(p_{e}\) = 10 N/m\(^{2}\), \(T_{e}\) = 300 K, and \(c_{1e}\) = 0.23 [6].

The system of equations with initial and boundary conditions was reduced to a discrete form by the control volume method [11]. The grid equations resulting from discretization were solved by the SIP method [11]. The method of splitting into physical processes was used; i.e., initially the structure of the flow and the distributions of scalar functions was calculated neglecting chemical reactions, and then the equations of chemical kinetics were solved taking into account the source terms in the equations for the temperature and concentrations of the components [6]. The whole computational domain is divided into 801 \(\times\)801 disjoint control volumes along the \(X\) and \(Y\) axes, respectively. In each control volume, a nodal point is specified. The sizes of control volumes on the boundaries were set equal to 0, and in the computational domain, equal to 0.5 m along the\(X\) and \(Y\) axes. Stability and convergence were tested by halving the sizes of the control volumes. As a result of numerical calculations, the critical sizes of breaks and barriers were obtained. Their difference is less than 1%.

RESULTS AND ANALYSIS

The above model was used to calculate combustion parameters for a crown forest fire in a pine forest taking into account fire breaks and barriers. The effect of fire barriers on the further spread of the fire front was investigated. Variable parameters were the wind velocity in the unperturbed medium and the sizes and position of the fire break and barrier.

To obtain reliable calculation results, it is important that the fire front has a steady velocity in approaching a barrier or break. Therefore, the initial boundary of the region of breaks and barriers was set at a distance of 40 m from the ignition source. The sizes of the entire region was 400 \(\times\)400 m along the \(X\) and \(Y\) axes, respectively.

We first considered the spread of the front of a forest crown fire in the presence of a fire break in the forest. The effect of the sizes of the break on the fire front spread was analyzed for a wind velocity \(v_e\) = 5, 8, 10, and 15 m/s and an FF moisture content \(W\) = 0.4. The distributions of isolines of temperature and concentrations of oxygen and pyrolysis products before and after the fire break were obtained. The gas-phase temperature was determined as\(\bar{T} =T/T_{e}\), where \(T_e\) = 300 K, and the concentrations of oxygen and combustible pyrolysis products in the fire front as \(\overline{c_1} = c_1/c_{1e}\) and \(\overline{c_2} = c_2/c_{1e}\), respectively. For the velocities considered, Figs. 2–5 show:

—the distributions of gas-phase isotherms for \(\bar{T}\) = 5 (1), 4 (2), 3 (3), 2.5 (4), 2 (5), 1.5 (6), and 1.3 (7);

 —oxygen concentration isolines for \(\overline{c_1}\) = 0.1 (1), 0.5 ( 2), 0.6 (3), 0.7 ( 4), 0.8 (5), and 0.9 (6);

—concentration isolines of volatile pyrolysis products for \(\overline{c_2}\) = 1.0 (1), 0.1 ( 2), 0.05 (3), 0.01 (4), 0.005 (5), and 0.001 (6).

The results of calculating the effect of the fire break size on the fire front spread at a wind velocity \(v_e\) = 5 m/s are shown in Fig. 2. Analysis of the location of isotherms and concentrations isolines of oxygen and volatile pyrolysis products before and after the fire break shows that the fire front overcomes a 20 \(\times\)30 m break and extends to the forest areas untouched by fire (Figs. 2a–2c). As the break size increases to 20 \(\times\)50 m, the temperature decreases and the fire does not have enough energy to continue to spread in the forest, as seen from the distribution of isotherms (Figs. 2d–2f).

At a wind velocity \(v_e\) = 8 m/s, the distribution of isolines in Figs. 3a–3c indicates that the fire front overcomes a 20 \(\times\)20 m break and spreads further. With an increase in the size to 20 \(\times\)30 m, the isotherms after the break correspond to low temperatures (Figs. 3d–3f), i.e., fire spread stopped.

At a wind velocity \(v_e\) = 10 m/s, the isolines in Figs. 4a–4c show that the fire front overcomes a 20 \(\times\) 20 m break and spreads further through the forest, and in the case of a 20 \(\times\)30 m break, the temperature after the break decreases (Figs. 4d–4f) so that the fire does not have enough energy to spread further through the forest.

At a wind velocity \(v_e\) = 15 m/s, the isotherms in Figs. 5a–5c show that the fire front overcomes a 20 \(\times\) 10 m break and spreads further through the forest, and as the break size increases to 20 \(\times\)20 m, the temperature after the break decreases (Figs. 5d–5f) and the fire does not spread further through the forest. At high wind velocities, the downwind direction (along the \(OX\) axis) of the fire front prevails, so that it expands only slightly and cannot overcome small breaks.

Thus, as a result of the calculations, we obtained the critical break sizes for which the fire overcomes the break and spreads further through the forest area. Analysis of the results shows that the best way to increase the effectiveness of the break is to increase its size along the \(OY\) axis (across the fire front spread direction). Figure 6 shows a curve of the break size \(L_{y}\) versus wind velocity \(v_e\) at a constant value \(L_ {x}\) = 20 m.

In this work, we also considered another forest fire fighting facility—a fire barrier of finite size—and investigated its effect on the fire front spread. Barriers consist mainly of deciduous trees with a moisture content \(W\) \(>\)1.0. Calculations were carried out at wind velocities \(v_e\) = 5, 8, 10, and 15 m/s and an FF moisture content \(W\) = 0.4. For the wind velocities considered, Figs. 7–10 show:

—the distributions of gas-phase isotherms for \(\bar {T}\) = 5 (1), 4 (2), 3 (3), 2.5 (4), 2 (5), 1.5 (6), and 1.3 7);

—concentration isolines of oxygen for \(\overline {c_1}\) = 0.1 (1), 0.5 (2), 0.6 (3), 0.7 (4), 0.8 (5), and 0.9 (6);

—concentration isolines of volatile pyrolysis products for 1.0 (1), 0.1 (2), 0.05 (3), 0.01 ( 4), 0.005 (5), and 0.001 (6).

At \(v_e\) = 5 m/s, as can be seen from Figs. 7a–7c, the fire overcomes a 40 \(\times\)40 m barrier and spreads to new areas of the forest. Increasing the barrier size to 40 \(\times\)50 m leads to a stop of fire spread (Figs. 7d–7f).

For \(v_e\) = 8 m/s, the distribution of isolines in Figs. 8a–8c show that the fire front overcomes a \(20 \times 20\) m barrier and spreads further through the forest. Increasing the barrier size to 40 \(\times\)20 m leads to a stop of fire spread (Figs. 8d–8e).

At \(v_e\) = 10 m/s, the fire front also overcomes a \(20\times 20\) m barrier and continues to spread (Figs. 9a–9c). As the barrier size increases to 40 \(\times\)20 m, the fire front does not spread to new areas of the forest (Figs. 9d–9f).

At \(v_e\) = 15 m/s, the fire front overcomes a \(40\times 40\) m barrier and continues to spread (Figs. 10a–10c). Increasing the barrier size to 40 \(\times\)60 m leads to a decrease in the temperature of the fire front after the break (Figs. 10d–10f), i.e., the fire spread stops.

Thus, we obtained the critical sizes of fire barriers for which the fire overcomes the barrier and spreads further through the forest. From the results it follows that increasing the efficiency of barriers contributes to an increase in its size both along the\(OX\) and \(OY\) axes. Figure 11 shows a curve of the size \(L_{y}\) versus the wind velocity \(v_e\) for a constant value \(L_{x}\)= 40 m.

It is found that the rate of forest fire spread is most strongly affected by wind velocity and the amount and moisture content of FF. At some critical sizes of fire breaks and barriers, burning in the fire front stops due to the large expenditure of thermal energy for heating and drying of FF, which is not compensated by heat release in the fire front. The movement of the forest fire front in time can be traced by changes in the location of combustion temperature isotherms. Analysis of the results showed that the creation of fire breaks is the most effective measure for forest fire prevention and an alternation of fire barriers and breaks is effective for preventing the spread of crown forest fires.

CONCLUSIONS

The physicomathematical formulation of the problem presented in the paper can be used to theoretically describe different conditions of forest fire spread taking into account weather conditions, the   state   of   forest fuels, and the presence of fire breaks and barriers. The calculated distributions of temperature and concentrations of oxygen and pyrolysis products over time allow evaluation of the dynamics of the crown fire front. From the results of calculations, the minimum sizes of fire breaks and barriers for which the fire front spread stops were determined depending on the amount, type, and moisture content of FF, and the wind velocity and direction. Thus, the model can be used to develop measures for extinguishing forest fires.