Reversible binding of oxygen with hemoglobin is essential for the function of the oxygen-transporting system of the blood [1, 2]. The oxyhemoglobin dissociation curve shows graphically how the degree of hemoglobin oxygenation depends on the partial pressure of oxygen [3, 4]. Oxyhemoglobin dissociation curves are constructed using a limited set of discrete experimental data and can then be approximated with a number of mathematical functions [5]. Approximation is necessary primarily for estimating the oxygen tension at which hemoglobin is half saturated (p50) [6, 7], the full-saturation tension (p95) [8], and the degree of oxygenation in the arterial (SaO2) [9, 10] or venous (SvO2) blood [11, 12].

Current mathematical models of oxygenation make it possible to associate the equation coefficients with certain parameters characterizing the oxygen-binding properties of a hemoprotein [13–15]. We have previously assessed the approximation potential of the most common models that describe oxygen binding with hemoglobin and are based on power and exponential functions [16].

However, high values of the approximation validity factor r2 are not self-sufficient and determinant in selecting the oxygenation model. This is explained by the fact that high r2 values are possible to achieve using higher-order interpolating polynomials, such as Lagrange, Newton, Fourier, Chebyshev, and other polynomials, which lack physical significance in this case [17–19].

The Hill equation consequently remains in use, although it provides only an approximate description of the oxygen-binding properties of hemoglobin. Its advantage is that a minimal set of a priori data is necessary for describing the oxygenation process [20] (the equation is broadly used to describe other cooperative processes as well). The Hill coefficient h is a parameter of the Hill equation and can be used to characterize the degree of cooperativity for the oxygenation process. However, the physical significance of the Hill coefficient is difficult to understand because the number n of interacting subunits of the tetramer does not correspond to non-integer h values [21–23].

In this work, we attempted to resolve the apparent discrepancy by introducing a coupling coefficient that clarifies the physical significance of the Hill equation. Note that a reinterpretation of the Hill coefficient may be of importance for describing ligand–receptor interactions [24] and other cooperative systems.

METHODS

We used the Hill model and a set of published experimental data [25]. Model parameters were optimized by the least squares method [26]. The necessary calculations were performed using MS Excel spreadsheets.

RESULTS AND DISCUSSION

The oxygenation equation that Hüfner [27] proposed in 1890 on the basis of the law of mass action fails to describe the S shape of the oxyhemoglobin dissociation curve. In 1910, Hill [13] consequently assumed that oxygenation can be considered as the interaction of a ligand with a macromolecular protein associate, that is, as a chemical reaction of the n-th order:

$${{({\text{Hb}})}_{n}} + n{{{\text{O}}}_{2}} \rightleftharpoons {{({\text{Hb}}{{{\text{O}}}_{2}})}_{n}},$$
(1)
$$y = \frac{{{{p}^{n}}}}{{p_{{50}}^{n} + {{p}^{n}}}},$$
(2)

where Hb is deoxyhemoglobin, O2 is oxygen, HbO2 is oxyhemoglobin, y is the degree of hemoglobin saturation with oxygen, p is the partial pressure of oxygen, p50 is the partial pressure of oxygen at y = 0.5 (50% saturation with the ligand), and n is the degree of hemoglobin aggregation (the ligand-based reaction order, which coincides with the stoichiometric coefficient of the reaction when the law of mass action is obeyed).

The power n usually took non-integer values in data analyses, and the physical significance of the Hill equation was consequently unclear. To explain the non-integer values of the Hill coefficient, Hill proposed that n be considered as a parameter averaged over many molecular hemoprotein associates varying in degree of aggregation [13, 28].

However, Adair et al. [14] showed in 1925 that the hemoglobin molecule is a tetramer. This finding did not contradict the concept of molecular associates but failed to explain why values lower than 4 are assumed by the Hill coefficient. This mismatch led again to discrepancies in the physical interpretation of the Hill model [21–23].

A pool of hemoglobin molecules can be considered as a set of dimeric and tetrameric forms present in different proportions by weight, similar to hemoprotein associates. However, the tetrameric form accounts for the vast majority (99.3–99.4%) of hemoglobin found in red blood cells, as follows from calculations with the reference hemoglobin concentration in the cell (4300–5500 μmol/L) [29], the dissociation constant (K4.2 = 0.2 μmol/L) at a normal atmospheric pressure, pH 7.0, and a temperature of 37°C [30]. Therefore, a Hill coefficient of 2.52. (as we calculated using published data [25]) should correspond to a tetramer portion of 25.9%. This is possible at a protein concentration of 0.1 μmol/L and apparently contradicts the above values.

Still the Hill equation is used broadly because respective calculations are simple to perform and the approximating potential of the equation is good enough [31]. The equation makes it possible to determine p50 in a straightforward manner, and the Hill coefficient (also designated nH [32, 33], h [34, 35], other symbols, or their combinations [36, 37]) reflects to a certain extent the cooperativity of hemoglobin subunits.

To eliminate the discrepancy between the potential of the Hill equation to approximate the experimental data well, and the potential of the equation power to assume non-integer values [38], we propose that the Hill coefficient h be conceived of as a product of the number n of interacting structural elements (in particular, hemoprotein subunits) and the proportionality factor a, which is understood as the degree of cooperativity in the interaction of the elements:

$$y = \frac{{{{p}^{{an}}}}}{{p_{{50}}^{{an}} + {{p}^{{an}}}}}.$$
(3)

However, when cooperativity is lacking, which corresponds to the Hill coefficient h = 1, the proportionality factor a assumes various values depending on the subunit number n, and n is consequently difficult to interpret.

We propose that the product an in the Hill equation is written in the following form:

$$h = an = \theta (n)(n - 1) + 1,$$
(4)

where θ(n) is a new parameter that we introduce as a relative coefficient of cooperativity of a protein consisting of n subunits. Then θ(n) = 0 suggests lack of cooperativity, and the respective Hill coefficient is unity at any n.

Our modifications yield the following final form of the Hill equation (at p > 0):

$$y = \frac{{{{p}^{{\theta (n)(n - 1) + 1}}}}}{{p_{{50}}^{{\theta (n)(n - 1) + 1}} + {{p}^{{\theta (n)(n - 1) + 1}}}}} = {{\left( {1 + {{{\left( {\frac{{{{p}_{{50}}}}}{p}} \right)}}^{{\theta (n)(n - 1) + 1}}}} \right)}^{{ - 1}}}.$$
(5)

Fisher’s test was used to check whether the above mathematical model is adequate and fits the experimental data [25]. A one-factor regression analysis showed that Fcalc(103905.36) ≫ Ftabl (3.99, α = 0.05) with r2 = 99.94%, demonstrating that the model is statistically significant.

Using Eq. (5) and the data available for tetrameric hemoglobin, p50 and θ(n) were calculated to be 28.8 mm Hg and 0.507, respectively. Thus, the coefficient can be used to describe the degree of interaction between subunits in an oligomer. The coefficient shows the extent to which protomers should interact to allow the macromolecule to perform its current function based on its maximal functional capacity, which depends on its number of subunits.

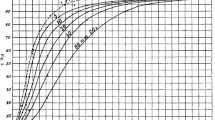
An important possible application of θ(n) is comparing the degree of cooperativity, for example, for dimeric and tetrameric hemoglobin forms with due regard to the number of interacting subunits. While dissociation of a hemoprotein tetramer into dimers will expectedly decrease the Hill coefficient, the degree of cooperativity measured by normalized θ(n) may remain the same. In a general form, normalized θ(n) can be obtained by transforming to a dimeric, tetrameric, or another form of the protein on the basis of the dependences shown in Fig. 1. Boundary conditions are also important to note. When a molecule consists of one subunit (n = 1), the θ(n) value is not determined (dashed line 1*) because there is no cooperativity as a physical phenomenon. When θ(n) = 0, the Hill coefficient is always unity at every n > 1 (Fig. 1).

Fig. 1.
figure 1

The relative coefficient of cooperativity as a function of the Hill coefficient for a macromolecule consisting of n subunits. The values n = 2 and 4 are of importance in the case of the hemoglobin molecule. Ordinal numbers of linear models correspond to the number of subunits in a macromolecule. θ(n) value is undefined in the case of n = 1. In the case of n → ∞ and h = const, θ(n) → 0.

Full size image

When there is a mixture of dimeric and tetrameric forms with an average n in a hemoglobin solution, θ(n) can be obtained from the calculated n value of the given range (Table 1).

Table 1. The portion χ of tetrameric hemoglobin forms and the arithmetic mean number \(\bar {n}\) of subunits per macromolecule as functions of the protein concentration C
Full size table

Another important possible application of the new parameter θ(n) is studying the degree of interaction cooperativity for valence hybrids and, in particular, hemoglobin heterotetramers as combinations of α, β, and other subunits differing in oxidation degree of the heme iron (2+ or 3+).

CONCLUSIONS

Using hemoglobin oxygenation as an example, a modification was proposed for the Hill equation, which describes the cooperative binding of a ligand with a macromolecule. The relative coefficient of cooperativity θ(n) was introduced as a means to couple the calculated Hill coefficient with the number n of interacting subunits in an oligomer and to overcome the problem of the physical significance of the Hill coefficient by explaining the nature of its non-integer values. Normalization of the relative coefficient of cooperativity additionally offers the possibility to compare its values for oligomers with different n values.

To summarize, θ(n) may provide a useful tool to solve a broad range of problems related to cooperative interactions [39–41]. Our approach can be used to describe the absorption isotherms (binding curves) of various ligands and macromolecules, in particular, the interaction of receptors with their mediators [46, 47].