The Laws of Waterfowl Motion and Their Use in the Movement of Underwater Objects

Abstract

In terms of an ideal incompressible fluid, the flow of a thin wing of finite span, which simulates the work of a dolphin’s tail fin, is considered. The motion of a dolphin performing periodic oscillations perpendicular to the direction of the main motion with its tail fin with an almost uniform and rectilinear motion of the center of mass is studied. The flow around an oscillating wing operating in the mode of creating a thrust force with the formation of a swirling trace behind the wing is studied. The model parameters are selected according to the data of the experimental observations. A numerical solution of the problem is obtained with calculations of the kinematic and power characteristics of the dolphin tail fin model.

INTRODUCTION

Interest in the study of the flow around animals moving in the marine environment (primarily dolphins and cetaceans), as well as in biomechanics, is related to the development of shipbuilding: both surface ships and underwater technical structures. It is equally important to include the improvement of self-propelled underwater objects (SUOs). In relation to this, researchers are particularly interested in the problem of creating new types of vehicles, the principles of which are based on the use of methods and means developed by nature for waterfowl in accelerated motion in the marine environment with the minimal possible effort. At the same time, long-term biological evolution, guided and stimulated by the struggle for existence, has led to the development in animals of the most rational ways of swimming and flying. Therefore, the study of the mechanisms of the formation of the thrust and lifting force in biological species in wildlife can serve as one of the approaches to solve problems of improving the motion of modern vehicles, taking into account the action of the mechanism with analogs of the work, for example, of the tail fin of a dolphin (and other biological species) or the oscillating wing in birds acting as working elements [1, 5, 7, 13, 14].

In the conducted studies, the parameters of the biomodels were chosen in accordance with the observational data [2, 3, 5, 8]. As a result, based on processing the experimental data using special programs compiled earlier by the authors and the corresponding numerical calculations, new information in the field of biohydrodynamics was obtained with the possibility of using it in problems of improving the dynamic characteristics of objects flowing around under water. These studies can be used to create tools for the coverage of the underwater environment in the coastal seas of Russia.

EXPERIMENTAL DATA ON DOLPHINS SWIMMING

It is well known that the motion of large fast-swimming animals, such as dolphins, are characterized by large Reynolds numbers ${\text{Re}} = {{VL} \mathord{\left/ {\vphantom {{VL} \nu }} \right. \kern-0em} \nu } \gg 1$ [16] ($V$ is the average speed, $L$ is the length of the animal, and $\nu$ is the kinematic coefficient of the water’s viscosity). The value of ${\text{Re}}$ for various fish and cetaceans under normal swimming conditions varies within ${{10}^{4}} < {\text{Re}} < {{10}^{8}}$. In experiments to determine the kinematic characteristics of dolphins swimming, the number ${\text{Re}}$ changed from $3 \times {{10}^{6}}$ to $1.4 \times {{10}^{7}}$ [3].

Dolphins have a streamlined shape and swim without separation of the flow from the body. In [11] experiments have shown that up to the tail fin (at values ${x \mathord{\left/ {\vphantom {x L}} \right. \kern-0em} L} < 0.89$, here $0 \leqslant x \leqslant L$ and $x$ is the distance from the front point of the nose of the model to the fixed section), the flow around the dolphin is continuous. At the same time, on a rigid dolphin model, on its entire back half (with ${x \mathord{\left/ {\vphantom {x L}} \right. \kern-0em} L} \geqslant 0.55$), the separation mode of the flow is realized. Direct observations of dolphins swimming in the conditions of bioluminescence (glow) of the sea also testify to the continuous flow around the dolphin. Cases have been recorded when researchers observed how at night, in calm weather in the sea, only two luminous cords remain behind a swiftly swimming dolphin, and a wide luminous area behind a swimming seal. It is well known that a dolphin swims almost without disturbing the calm state of the water [12]. The boundary layer adjacent to the surface of its body is thin. The greatest thickness of the boundary layer (at the end near the tail) is usually no more than a few percent of the animal’s thickness [16]. Dolphins have an elongated body shape and a strong constriction in front of the caudal fin (for example, the ratio of the diameter of the body of a bottlenose dolphin to its length is approximately 1 : 6 [4]). Thus, the caudal fin of a dolphin practically moves in an undisturbed flow, and the effect of the dolphin’s body on the operation of its caudal fin can be neglected [4].

KINEMATIC AND FORCE MODELS OF A DOLPHIN’S TAIL FIN

To create the necessary thrust force, the dolphin performs oscillations with its tail fin perpendicular to the direction of the main movement with amplitudes of the order of the transverse dimensions of the entire body. In this case, the flow around the tail fin of a dolphin can be formulated as a problem of the nonstationary flow around an incompressible fluid flow around a wing of finite span, which oscillates with a large amplitude.

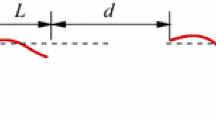
The results of studying the kinematic characteristics of dolphins swimming in natural conditions, in a sea basin, in a biohydrodynamic channel [1–3, 8, 10] show that in a prolonged unchanged swimming mode, all points of the dolphin’s body describe wave-like trajectories of the smallest span for points of the body mass close to the center; and the largest span, for the points of the caudal fin. The amplitude of the oscillations of the center of mass of the animal is only a few percent of the amplitude of oscillations of the point of the fork of the caudal fin. In practice, we can assume that the center of mass moves in a straight line. In this case, the trajectory of the caudal fin bifurcation point was analyzed by successive or selective oscillation cycles (Fig. 1). As a result, the translational movement of the dolphin in this cycle corresponded to the position of the trailing line $AB$ drawn from the starting point $A$ to the end point $B$ of the trajectory of this cycle. The length of the segment $AB$ is designated as the wavelength ${{\lambda }_{w}}$, and the span of the wave as ${{A}_{w}}$.

Fig. 1.

The trajectory of the fork point of the caudal fin.

The results of experimental studies to determine the kinematic characteristics of the bottlenose dolphin swimming carried out in a biohydrodynamic channel with a square cross section $4{\text{ }}{{{\text{m}}}^{2}}$ are shown in Fig. 2 [2]. The elements of the caudal fin of the dolphin were recorded on film. For subsequent processing, the film frames of those experiments were selected in which the trajectory of the dolphin’s center of mass was almost rectilinear and close to the horizontal axial line of the channel, and the caudal fin did not perform rotational movements around the root chord. In other words, in these experiments, the fin was projected on the vertical plane (the side wall of the channel) only by the root profile, which was replaced by its root chord.

Fig. 2.

Dependences of the kinematic characteristics of the swimming of the bottlenose dolphin: (a) the position of the root chord AB of the fin at successive time moments $t$; (b, c) velocities of the tail fin point (point $O{\kern 1pt} '$); (d, e) dependences of angles $\gamma ,\,\,\beta$ and $\alpha$ on time; (f) the position of the root chord in the coordinate system ${{y}^{1}},{{y}^{2}},{{y}^{3}}$; $h$ is the amplitude of vertical oscillations, ${{V}_{*}}$ is the speed of point O ', and $n$ are the film frame numbers.

The positions of the root chord of the fin are shown in Fig. 2a on the plane $xOy$ at successive time moments. The time $t$ in seconds and the number of film frames $n$ corresponding to the positions of the root chord of the fin are plotted along the $x$ axis. The time dependent horizontal ${{V}_{0}}$ and vertical ${{V}_{y}}$ velocity components (in m/s) of some point of the caudal fin are shown in Figs. 2b and 2c. This point will be considered given on the root chord of the fin (point O′ in the center). The dependences of the angles $\gamma ,\,\,\beta$, and $\alpha$ on time are presented in Fig. 2. Angle $\gamma$ is defined as the angle of inclination of the velocity vector of the given point to the direction of the dolphin’s translational motion, to the $x$ axis, $\beta$ is the instantaneous angle of inclination of the root chord to the $x$ axis, and $\alpha = \gamma - \beta$ is the angle of attack, the angle between the velocity vector of the considered point and the root chord of the fin. Moreover, the maximum angle of attack $\alpha$, obtained from the analysis of the trajectories of the caudal fin points, as a rule, did not exceed $10^\circ$, and the average values lie within ±($4^\circ {\kern 1pt} - {\kern 1pt} 6^\circ$).

Note that, by analogy with [15], using the data in Fig. 2, we can schematically represent the typical propulsion mechanism of marine animals: the caudal fin moves in such a way that, at each half-cycle of oscillation, a force is generated that acts in the direction of the horizontal motion of the animal. The lifting force for the period with such a movement is almost zero¹.

Next, the tail fin of the dolphin will be modeled with a thin flat wing. We assume that the wing performs periodic angular oscillations around a horizontal axis fixed in the wing plane and parallel to the straight trailing edge. In turn, the axis of angular oscillations, located across the direction of the main movement, performs vertical harmonic oscillations. A diagram of the flow around the wing is shown in Fig. 3.

Fig. 3.

Wing flow pattern (see explanations below in the text).

Here it can be assumed that, using an infinitely thin wing, it is appropriate to represent a real wing with a rounded edge ${{L}_{S}}$, streamlined without flow separation, and a sharp edge ${{L}_{W}}$, from which a vortex trace that appears behind the wing during its movement flows smoothly flows into the fluid flow. We can assume that the wing is a bearing surface $s$ with the leading edge ${{a}^{1}} = 0,$ $- 1 \leqslant {{a}^{2}} \leqslant 1,$ streamlined without separation, on which the suction force acts [6, 15]. From the trailing ${{a}^{1}} = 1$, $- 1 \leqslant {{a}^{2}} \leqslant 1$ and side $- 1 \leqslant {{a}^{1}} \leqslant 1,$ ${{a}^{2}} = \pm 1$ edges, a free vortex surface $w$ flows into the flow. The leading edge ${{a}^{1}} = 0,$ $- 1 \leqslant {{a}^{2}} \leqslant 1$ is the leaking edge ${{L}_{S}}$, the trailing ${{a}^{1}} = 1$, $- 1 \leqslant {{a}^{2}} \leqslant 1$ and side edges $0 \leqslant {{a}^{1}} \leqslant 1,$ ${{a}^{2}} = \pm 1$ are the run-off edge ${{L}_{W}}$; and ${{a}^{1}}\,\,{\text{and}}\,\,{{a}^{2}}$ are the Lagrangian coordinates of the point of the bearing surface $s$.

Thus, in the Cartesian coordinate system ${{x}^{1}},{{x}^{2}},{{x}^{3}}$, the flow at infinity is assumed to be uniform with a constant velocity ${{V}_{\infty }}$, parallel to the ${{x}^{1}}$ axis, and directed in the positive direction of this axis. We describe the motion of the wing in the coordinate system ${{y}^{1}},{{y}^{2}},{{y}^{3}}$ (Fig. 2f), in which the fluid is at rest at infinity and whose axes are parallel, respectively, to the axes of the coordinate system ${{x}^{{\text{1}}}}{\text{,}}{{x}^{{\text{2}}}}{\text{,}}{{x}^{{\text{3}}}}$. The axis of angular oscillation, parallel to the ${{y}^{2}}$ axis, moves along the vertical axis according to the law ${{y}^{{\text{3}}}} = h{\text{cos(}}wt{\text{)}}$; and along the horizontal axis, according to the law ${{y}^{1}} = - {{V}_{\infty }}t$. The wing is projected onto the plane ${{y}^{1}}{{y}^{3}}$ by the root chord $AB$; and the axis of angular oscillations, by point $O{\kern 1pt} '$ (see Fig. 2f). Thus, the position of the wing at each moment of time is determined by the position of the axis of angular oscillations and the angle of inclination of the chord $AB$ to the ${{y}^{1}}$ axis by angle $\beta$. The angle of attack of the wing $\alpha$ is defined as the angle between the instantaneous velocity vector of the rotation axis ${{{\mathbf{V}}}_{*}}$ and wing chord $AB$. Angle $\gamma$ is the angle between the vector ${{{\mathbf{V}}}_{*}}$ and axis ${{y}^{1}}$.

The tail fin of a dolphin is an underwater hydrodynamic wing with a symmetrical profile of complex shape in plan. Figure 4, as an example, shows the profile of the caudal fin of a dolphin from [9], which describes the caudal fins of dolphins and whales. It is shown that the main profile of the caudal fins of cetaceans is the generalized symmetrical profile of Zhukovsky NEZH-I with some changes in the rear part.

Fig. 4.

Model profile of the caudal fin of a dolphin from [9].

Figure 4 shows that the shape of wing 1 in the plan view appears to be a relatively good approximation to the shape of the caudal fin of a dolphin. Based on this, the movement of wing 1 can be described by Eqs. (1):

$$\begin{gathered} {{x}^{1}} = \left\{ {b\left[ {{{a}^{1}} + {{c}_{0}}(1 - {{a}^{1}}){{{({{a}^{2}})}}^{2}}} \right] - {{b}_{0}}} \right\} \\ \times \,\,\cos \beta (t) + {{b}_{0}}, \\ {{x}^{2}} = b\lambda \left( {1 - {{{{c}_{0}}} \mathord{\left/ {\vphantom {{{{c}_{0}}} 3}} \right. \kern-0em} 3}} \right){{{{a}^{2}}} \mathord{\left/ {\vphantom {{{{a}^{2}}} 2}} \right. \kern-0em} 2}, \\ {{x}^{3}} = \left\{ {b\left[ {{{a}^{1}} + {{c}_{0}}(1 - {{a}^{1}}){{{({{a}^{2}})}}^{2}}} \right] - {{b}_{0}}} \right\} \\ \times \,\,\sin \beta (t) + h\cos (\omega t), \\ 0 \leqslant {{a}^{1}} \leqslant 1,\,\,\,\, - {\kern 1pt} 1 \leqslant {{a}^{2}} \leqslant 1, \\ \beta (t) = \gamma (t) - \alpha (t), \\ \gamma (t) = {\text{arctan}}\left( {\frac{{\omega h}}{{{{V}_{\infty }}}}\sin (\omega t)} \right), \\ \alpha (t) = {{\alpha }_{0}}\sin (\omega t), \\ \end{gathered} $$

(1)

where ${{a}^{1}}$ and ${{a}^{2}}$ are the Lagrangian coordinates of the wing points, $\lambda$ is the wing extension, $\omega$ is the oscillation frequency, ${{c}_{0}}$ is the parameter that specifies the shape of the wing in plan, $h$ is the amplitude of the vertical oscillations of the axis of angular oscillations, and ${{b}_{0}}$ is the position of the vertical oscillation axis, i.e., the distance in the root section ${{a}^{2}} = 0$ between the point of the leading edge of the wing and the point of the considered axis (positive if the axis is behind the leading edge).

The wing extension $\lambda = {{4{{l}^{2}}} \mathord{\left/ {\vphantom {{4{{l}^{2}}} S}} \right. \kern-0em} S}$, where $l$ and $S$ are the half-span of the wing and its area, respectively, were calculated by the formula $S = 2bl(1 - {{{{c}_{0}}} \mathord{\left/ {\vphantom {{{{c}_{0}}} 3}} \right. \kern-0em} 3})$. Then the parameter ${{c}_{0}} = 3(1 - {{2l} \mathord{\left/ {\vphantom {{2l} {\lambda b}}} \right. \kern-0em} {\lambda b}})$.

Further, the equations of motion of the wing are dimensionless and reduced to the form

$$\begin{gathered} {{x}^{1}} = \left[ {{{a}^{1}} + {{c}_{0}}(1 - {{a}^{1}}){{{({{a}^{2}})}}^{2}} - b_{0}^{{{'}}}} \right] \\ \times \,\,\cos \beta (t) + b_{0}^{{{'}}}, \\ {{x}^{2}} = \lambda \left( {1 - {{{{c}_{0}}} \mathord{\left/ {\vphantom {{{{c}_{0}}} 3}} \right. \kern-0em} 3}} \right){{{{a}^{2}}} \mathord{\left/ {\vphantom {{{{a}^{2}}} 2}} \right. \kern-0em} 2}, \\ {{x}^{3}} = \left[ {{{a}^{1}} + {{c}_{0}}(1 - {{a}^{1}}){{{({{a}^{2}})}}^{2}} - b_{0}^{{{'}}}} \right] \\ \times \,\,\sin \beta (t) + h{\kern 1pt} '\cos (\omega {\kern 1pt}^{{'}}t), \\ 0 \leqslant {{a}^{1}} \leqslant 1,\,\,\,\, - {\kern 1pt} 1 \leqslant {{a}^{2}} \leqslant 1, \\ \beta (t) = \gamma (t) - \alpha (t), \\ \gamma (t) = \arctan \left( {\omega {\kern 1pt}^{{'}}h{\kern 1pt} '\sin (\omega {\kern 1pt}^{{'}}t)} \right), \\ \alpha (t) = {{\alpha }_{0}}\sin (\omega {\kern 1pt}^{{'}}t), \\ \end{gathered} $$

(2)

with the following parameter values:

$$\begin{gathered} {{c}_{0}} = {3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}\,\,\,\,\left( {{\text{wing}}\,\,1} \right),\,\,\,\,0.5 \leqslant h{\kern 1pt} ' \leqslant 1.5, \\ \lambda = 4,\,\,\,\,{{\alpha }_{0}} = {{10}^{^\circ }}, \\ 0.2 \leqslant \omega {\kern 1pt}^{{'}} \leqslant 1.5,\,\,\,\,0 \leqslant b_{0}^{{{'}}} \leqslant 1.5. \\ \end{gathered} $$

Here $h{\kern 1pt} ' = {h \mathord{\left/ {\vphantom {h {b,}}} \right. \kern-0em} {b,}}b{\kern 1pt} ' = {{{{b}_{0}}} \mathord{\left/ {\vphantom {{{{b}_{0}}} {b,}}} \right. \kern-0em} {b,}}\,\,{\text{and}}\,\,\omega {\kern 1pt} ' = {{\omega b} \mathord{\left/ {\vphantom {{\omega b} {{{V}_{\infty }}}}} \right. \kern-0em} {{{V}_{\infty }}}}$ are, respectively, the dimensionless amplitude of the vertical oscillations of the axis of angular oscillations, the position of this axis, and the frequency of oscillations.

For dimensionless coordinates and dimensionless time, the designations corresponding to dimensional quantities are retained. In this case, the wing is considered rigid, since there are no large deformations in the main part of the fin [5].

The values of the kinematic parameters and their ranges of the change in this study were obtained as a result of processing the experimental data of the works [3, 10]. The geometric dimensions and body weight of the experimental animals are given in Table 1 [4]. Amplitude $h{\kern 1pt} '$ and frequency $\omega {\kern 1pt}^{{'}}$ were calculated according to the formulas $h{\kern 1pt} ' = {{{{A}_{0}}} \mathord{\left/ {\vphantom {{{{A}_{0}}} b}} \right. \kern-0em} b}$ and $\omega {\kern 1pt} {\kern 1pt} ' = {{2\pi fb} \mathord{\left/ {\vphantom {{2\pi fb} {{{V}_{0}}}}} \right. \kern-0em} {{{V}_{0}}}}$, where ${{A}_{0}}$ and $f$ are the experimentally observed values of the amplitude and frequency of oscillations of the point of the fork of the caudal fin; ${{V}_{0}}$ is the speed of movement of the center of mass of the dolphin’s body; and the length of root chord of the fin $b$ was taken to be $0.1L$. Note that the ratio ${b \mathord{\left/ {\vphantom {b L}} \right. \kern-0em} L}$ in the six experimental dolphins (Table 1) varies from $0.085$ to $0.121$. The amplitude of the change in the angle of attack ${{\alpha }_{0}}$ was taken to be ${{10}^{^\circ }}$ (see Fig. 2e), and the average angle of attack $\bar {\alpha }$ on the half-cycle of the oscillation was determined by the formula

$$\bar {\alpha }(t) = \frac{2}{T}\int\limits_0^{{T \mathord{\left/ {\vphantom {T 2}} \right. \kern-0em} 2}} {\alpha (t)dt} \approx {{6}^{^\circ }},$$

which approximately corresponds to the data presented in Fig. 2.

Table 1.   Geometrical and kinematic characteristics of experimental dolphins

FLOW AROUND THE MODEL AND THE EFFICIENCY OF A DOLPHIN’S TAIL FIN

The system of equations with the corresponding initial and boundary conditions, which describes the flow around a wing with the given law of motion (2), is given in [7, 13, 14].

The numerical solution method is presented in [7].

The instantaneous ${{C}_{{{{T}_{i}}}}}$ and average ${{C}_{T}}$ thrust coefficients and wing efficiency $\eta$ are determined based on the results of the numerical solution. The coefficient ${{C}_{{{{T}_{i}}}}}$ was defined as the ratio of the instantaneous traction force to the value ${{\rho V_{\infty }^{2}S} \mathord{\left/ {\vphantom {{\rho V_{\infty }^{2}S} 2}} \right. \kern-0em} 2}$, where $\rho$ is the density of the liquid and $S$ is the wing area. The period-averaged coefficient ${{C}_{{{{T}_{i}}}}}$ is equal to the coefficient ${{C}_{T}}$. Note that the coefficient $\eta$ is the ratio of the average useful power equal to the product of the thrust force averaged over the period and the speed of the oncoming flow to the average power over the period of oscillations expended on the implementation of the oscillatory motion of the wing.

Figure 5 graphically shows The dependences of the thrust force coefficient ${{C}_{T}}$ and hydrodynamic efficiency coefficient $\eta$ on the oscillation frequency $\omega {\kern 1pt} '$ in the case when the axis of angular oscillations passes through the point of the leading edge of the root section of the wing $(b_{0}^{{{'}}} = 0)$ and of the oscillation amplitude $h{\kern 1pt} ' = 1.0$. With this arrangement of the axis for wing 1, coefficient ${{C}_{T}}$ grows, and coefficient $\eta$ decreases with increasing oscillation frequency. At the same time, the coefficient of the thrust force is small $({{C}_{T}} \approx 0.25)$.

Fig. 5.

Dependences of the thrust force coefficient ${{C}_{T}}$ and hydrodynamic efficiency coefficient $\eta$ on the oscillation frequency $\omega {\kern 1pt} {\kern 1pt} '$ at $h{\kern 1pt} ' = 1.0$, when the axis of angular oscillations passes through the point of the leading edge (Fig. 5, here $b_{0}^{{{'}}} = 0$) and the trailing edge (Fig. 6, on the trailing edge $b_{0}^{{{'}}} = 1$) of the root section of the wing.

Dependences ${{C}_{T}} = {{C}_{T}}(\omega {\kern 1pt} ')$ and $\eta = \eta {\kern 1pt} (\omega {\kern 1pt} ')$ at $h{\kern 1pt} ' = 1.0$ in the case when the axis of angular oscillations passes through the point of the trailing edge of the root section of the wing $(b_{0}^{{{'}}} = 1)$ are shown in Fig. 6. The graphs show that when $h{\kern 1pt} '$ changes in the range from 0.5 to 1.5 there is a qualitative change in the nature of the dependence of the efficiency coefficient of wing 1 on the frequency of its oscillations. Thus, the coefficient $\eta$ at $h{\kern 1pt} ' = 0.5$ (curve 1) increases monotonically with increasing frequency. At $h{\kern 1pt} ' \approx 1.0$ and $h{\kern 1pt} ' = {\text{1}}{\text{.5}}$ (curves 2, 3), dependences $\eta (\omega )$ turn out to be nonmonotonic. In this case, with an increase in the amplitude of oscillations, the frequency at which $\eta$ has the maximum value, decreases:

$$\begin{gathered} \max \eta {\kern 1pt} (h{\kern 1pt} ' = 1.5,\omega {\kern 1pt} ^{{'}}) \equiv \max \eta {\kern 1pt} (h{\kern 1pt} ' = 1.5,\omega _{1}^{{{'}}}) \\ < \max \eta {\kern 1pt} (h{\kern 1pt} ' = 1.0,\omega {\kern 1pt} ^{{'}}) \equiv \max \eta {\kern 1pt} (h{\kern 1pt} ' = 1.0,\omega _{2}^{{{'}}}), \\ \max \eta {\kern 1pt} (h{\kern 1pt} ' = 1.0,\omega {\kern 1pt}^{{'}}) \equiv \max \eta {\kern 1pt} (h{\kern 1pt} ' = 1.0,\omega _{2}^{{{'}}}) \\ < \max \eta {\kern 1pt} (h{\kern 1pt} ' = 0.5,\omega {\kern 1pt}^{{'}}) \equiv \max \eta {\kern 1pt} (h{\kern 1pt} ' = 0.5,\omega _{3}^{{{'}}}), \\ \omega _{1}^{{{'}}} < \omega _{2}^{{{'}}} < \omega _{3}^{{{'}}}. \\ \end{gathered} $$

(3)

In Fig. 6 all graphs of the thrust force coefficient on the frequency of oscillations are increasing functions that increase faster with increasing $\omega {\kern 1pt}^{{'}}$ the greater $h{\kern 1pt} '$. The highest values of the thrust force coefficient ${{C}_{T}}$ of wing 1 are achieved at the highest values of amplitude $h{\kern 1pt} '$ and frequency $\omega {\kern 1pt} '$. From the analysis of the curves in Figs. 5 and 6, it follows that oscillations with larger amplitudes ($h{\kern 1pt} ' = 1.0$, $h{\kern 1pt} ' = {\text{1}}{\text{.5}}$) are preferable to oscillations with small amplitudes ($h{\kern 1pt} ' = 0.5$) to obtain higher values of the thrust force coefficient. In continuation of the analysis of the curves in Figs. 5 with the graphs in Fig. 6, we note that the coefficients ${{C}_{T}}$ and $\eta$ of wing 1 in the case $b_{0}^{{{'}}} = 0$ are much smaller than in the case $b_{0}^{{{'}}} = 1$.

Fig. 6.

Dependences of the thrust force coefficient ${{C}_{T}}$ and hydrodynamic efficiency coefficient $\eta$ on the oscillation frequency $\omega {\kern 1pt} '$ at $h{\kern 1pt} ' = 1.0$, when the axis of angular oscillations passes through the point of the leading edge (Fig. 5, here $b_{0}^{{{'}}} = 0$) and the trailing edge (Fig. 6, on the trailing edge $b_{0}^{{{'}}} = 1$) of the root section of the wing.

It is of interest to study the formation of a free vortex surface behind an oscillating wing. Such a study is complicated by the need for a three-dimensional consideration of the flow. Therefore, we confine ourselves to considering a free vortex surface in the plane of symmetry of the flow ${{x}^{2}} = 0$ of wing 1, oscillating at the parameter values $h{\kern 1pt} ' = 1$, $b_{0}^{{{'}}} = 1$, and $\omega {\kern 1pt} ' = 1$ (Fig. 7). It should be noted that in the section ${{x}^{2}} = 0$, the component $\gamma _{w}^{1}$ of the vector is identically equal to zero due to the symmetrical flow around the wing.

Fig. 7.

Position of the coordinate line ${{b}^{2}} = 0$ of the free vortex surface at time moments $\tau = 2\pi$ and $\tau = 3\pi$ (Fig. 7a); dots in the figure show the nodal points of the computational grid of the coordinate line ${{b}^{2}} = 0$, and their Lagrangian coordinates $b_{\nu }^{1} = \nu ,\nu = 0,1,2,...$ are given next to the dots. The structure of the free vortex surface behind the wing is shown in Fig. 7b.

The positions of the coordinate line ${{b}^{2}} = 0$ of the free vortex surface shown in Fig. 7 at time moments $\tau = {{\pi i} \mathord{\left/ {\vphantom {{\pi i} 2}} \right. \kern-0em} 2},{\text{ }}i = 4,6$ ($\tau = \omega t$ is dimensionless time) allow us to trace the development of a free vortex surface in time in the plane of symmetry of the flow ${{x}^{2}} = 0$. The root chord of the wing is shown in Fig. 7a as the segment $AB$ (point $A$ corresponds to the edge of the leakage of the root chord). The wing occupies, respectively, the extreme upper and lower positions at the instants of time $\tau = 2\pi i,i = 0,1,2,...$ and $\tau = (2j + 1)\pi ,{\text{ }}j = 1,2,...$. The dots in the figure show the nodal points of the computational grid of the coordinate line ${{b}^{2}} = 0$ [7]. This figure also shows the Lagrangian coordinates $b_{\nu }^{1} = \nu$ ($\nu = 0,1,2,...$) of the nodal points of the coordinate line ${{b}^{2}} = 0$.

An analysis of the calculation results shows that, over time, the free vortex surface twists around the points at which the vorticity intensity is maximum in absolute value. Figure 7a shows that the sections of the free vortex surface with the Lagrangian coordinates $b_{\nu }^{1} \approx 0{\kern 1pt} {\kern 1pt} - {\kern 1pt} 3$ and $b_{\nu }^{1} \approx 15{\kern 1pt} - {\kern 1pt} 17$ twist counterclockwise (at these points $\gamma _{w}^{2} < 0$; moreover, at the points $b_{\nu }^{1} = 2$ and $b_{\nu }^{1} = 16$, the dependence $\gamma _{w}^{2} = \gamma _{w}^{2}({{b}^{1}})$ has local minimums), and the section of the free vortex surface with the Lagrangian coordinates $b_{\nu }^{1} \approx 7{\kern 1pt} - {\kern 1pt} 10$ twists clockwise (at these points $\gamma _{w}^{2} > 0$ and the point $b_{\nu }^{1} = 8$ is a local maximum point).

Thus, after the establishment of a periodic mode of the flow around wing 1, brought into motion from a state of rest, the structure of the free vortex surface in the plane of symmetry of the flow has the form shown schematically in Fig. 7b.

Comparison of the calculation data with the experimental data [3, 10] suggests that dolphins move with the highest efficiency. In the experiments [3, 10], as noted above, the amplitude and frequency of oscillations of the point at the fork of the dolphin’s caudal fin were determined. If we assume that the movement of the dolphin’s caudal fin is described by law (2) with the axis of angular oscillations coinciding with the trailing edge, then the amplitude and frequency will be the amplitude and frequency of the axis of angular oscillations of the caudal fin model. (Here, the assumption about the localization of the axis of angular oscillations is natural, since it follows from the calculated data shown in Figs. 5 and 6 that, for the motion with the largest value of the coefficient $\eta$, the axis of angular oscillations should be located near the trailing edge.) In these experiments, the amplitude and frequency of the oscillations of the point at the fork of the caudal fin, corresponding to $h{\kern 1pt} ' \approx 1.0,$ $\omega {\kern 1pt}^{{'}} \approx 1.1$ [10], and $\omega {\kern 1pt} ' \approx 0.9$ [3], were mainly observed.

The calculations illustrated in Fig. 6 show that in the case $b_{0}^{{{'}}} = 1$ the highest value of the hydrodynamic coefficient of efficiency $\eta$ of wing 1 is achieved at $h{\kern 1pt} ' = 1.0$ and $\omega {\kern 1pt} ' = 1.15$ (curve 2). In Fig. 8, on the surface $\eta = \eta {\kern 1pt} (\omega {\kern 1pt} ',h{\kern 1pt} ')$, point $M$ corresponding to the largest value of the coefficient $\eta$ of wing 1, which is achieved with the specified values of the parameters $h{\kern 1pt} '$ and $\omega {\kern 1pt} '$, is highlighted.

Fig. 8.

Surface $\eta = \eta {\kern 1pt} (\omega {\kern 1pt} ',h{\kern 1pt} ')$ with highlighted point M, corresponding to the maximum value of the coefficient $\eta$ of wing 1, which is achieved at $h{\kern 1pt} ' = 1.0$ and $\omega {\kern 1pt} ' = 1.15$.

Thus, the results of the calculations for wing 1 are in agreement with the assumption that dolphins use the most rational movement mechanism when moving at a constant speed for a long time. In this case, the maximum possible part of the power expended on the oscillations of the tail fin is spent on the production of useful work to move the animal’s body. It was found in [3, 10] that with an increase in the amplitude of oscillations of the caudal fin in dolphins there is a tendency toward a decrease in the frequency of oscillations. According to the graphs in Fig. 6, from the hydrodynamic point of view, this happens because with an increase in the oscillation amplitude, the largest value of the coefficient ${{\eta }}$ is naturally achieved at lower vibration frequencies.

Therefore, it can be assumed that the hydrodynamic model of the caudal fin with a shape in plan close to the shape of the caudal fin of a dolphin satisfactorily describes the available experimental data on the kinematics of dolphins swimming.

To understand the mechanism of the formation of the thrust force of the tail fin, we can analyze the dependence of the instantaneous coefficient of the thrust force on time and find out the role of the contributions to this dependence of the suction force and the force due to the pressure drop on the wing. In Fig. 9 the solid line shows the dependence of the instantaneous coefficient ${{C}_{{{{T}_{i}}}}}$ of wing 1 on time $\tau$ at $h{\kern 1pt} {\kern 1pt} ' = 1$, $b_{0}^{{{'}}} = 1$, and $\omega {\kern 1pt} ' = 1$, and the dashed line is the contribution of the suction force. It can be seen that the thrust force of the caudal fin is created by the joint action of two mechanisms that complement each other. The thickened rounded leading edge of the caudal fin of the dolphin ensures the creation of a suction force of the required magnitude in that part of the period where the thrust force mechanism weakens the work due to the pressure differential and even where the latter becomes a braking force instead of a thrust force.

Fig. 9.

Dependence of the instantaneous coefficient ${{C}_{{{{T}_{i}}}}}$ pm time $\tau$ (solid line) and the contribution of the suction force in the creation of the thrust force (dashed line).

CONCLUSIONS

The calculations show that in the process of long-term evolution and natural selection, dolphins developed and consolidated the mechanism of movement, which was determined by the criterion of the greatest efficiency of the dolphins’ locomotor organs and the optimal use of various methods of creating the thrust force.