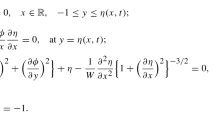Criterion of Applicability of the Theory of Long Waves for Describing Dispersive Tsunami Waves

Abstract

Conditions for the applicability of the dispersionless theory of long waves for reproducing dispersive tsunami waves are analyzed. The dispersive destruction distance is proposed for use as a quantitative criterion, a value that is uniquely determined by the wavelength that dominates in the spectrum of the initial elevation of the water surface in the tsunami source and by correction factor $\alpha .$ The physical meaning of value $\alpha$ is the fraction of the wavelength by which the dispersive wave packet lags behind the long-wave front when propagating over a distance equal to the dispersive destruction distance. Using the model residual displacement of the bottom surface, the geometrical parameters of which vary randomly, under the assumption of the instantaneous generation of waves and taking into account the smoothing effect of the water layer, the Monte Carlo method establishes a relationship between the accuracy of wave reproduction by the dispersionless model and the value $\alpha .$ Using the $\alpha$ coefficient scale, criteria previously proposed by other authors are ranked.

1 INTRODUCTION

Numerical modeling has proven to be an effective tool for studying and predicting tsunami waves (Gisler, 2008; Nosov, 2014; Behrens and Dias, 2015; Titov et al., 2016; Saito and Kubota, 2020). Models built on the basis of three-dimensional equations of hydrodynamics exist, but they are all used to reproduce waves in limited water areas (e.g., Shijo et al., 2016; Kozelkov et al., 2017; Nosov and Kolesov, 2019). The calculation of transoceanic or global tsunami propagation using 3D models is impossible due to the enormous computational complexity of the problem.

A significant gain in the amount of computation is achieved when using 2D models, which are built on the basis of hydrodynamic equations integrated along the vertical coordinate. This class includes the classical dispersionless equations of the theory of long waves (shallow water) and various types of Boussinesq equations (Madsen et al., 1991; Pelinovsky, 1996). Reducing the dimension of the problem (3D → 2D) limits the ability of models to describe the phase dispersion of gravity waves: classical shallow water equations do not reproduce dispersion in principle, while the Boussinesq equations can only reproduce weak dispersion.

Field observations show that phase dispersion is inherent in tsunami waves, as well as in any gravity waves on water (Kulikov et al., 2005; Watada et al., 2014; Levin and Nosov, 2016; Korolev et al., 2019; Saito, 2019). It is noteworthy that tsunami dispersion may be due not only to the vertical structure of wave currents, but also to a set of factors that are considered secondary (water compressibility, bottom elasticity, stratification, etc.). The influence of secondary factors is small, becoming significant only during transoceanic wave propagation (Watada et al., 2014). However, the classical (normal) dispersion of gravity waves on water, which affects the short-period components of the tsunami spectrum, can also manifest itself at relatively small distances from the source (tens and hundreds of kilometers), and even inside the source area. In this paper, we focus on the effect of classical dispersion.

Dispersion effects tend to accumulate as waves propagate. Since this accumulation occurs smoothly, there is no clear limit to which the theory of long waves can adequately describe dispersive tsunami waves. To determine such a limit, it is necessary to introduce a quantitative measure of the accuracy of the calculation of waveforms and set a certain value of this measure. The subjective assessment of the “degree of manifestation of dispersion” proposed by various authors obviously cannot lead to the development of a single quantitative criterion.

The problem of determining the limits to which the theory of long waves is able to adequately describe dispersive tsunami waves has concerned researchers since the very beginning of the era of numerical tsunami modeling. The first of these criteria (Kajiura, 1963, 1970; Shuto, 1991), we shall call it the Kajiura criterion, is based on the estimate of the value of the dimensionless parameter

$${{p}_{a}} = {{({{6H} \mathord{\left/ {\vphantom {{6H} R}} \right. \kern-0em} R})}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}({a \mathord{\left/ {\vphantom {a H}} \right. \kern-0em} H}),$$

(1)

where $H$ is ocean depth, $R$ is the distance traveled by the wave (distance from the source), and $a$ is the extent of the tsunami source in the direction of wave propagation. In accordance with the Kajiura criterion, dispersion effects can be neglected under the condition ${{p}_{a}} > 4.$ This criterion is applicable at large distances from the source: $R > 10a.$

In (Pelinovsky, 1982, 1996; Mirchina and Pelinovsky, 1982), the dimensional value dispersion length—the distance at which dispersion effects become noticeable (the Pelinovsky criterion)—is proposed for consideration:

$${{L}_{{\text{d}}}} = {{{{a}_{{\text{d}}}}{{\lambda }^{3}}} \mathord{\left/ {\vphantom {{{{a}_{{\text{d}}}}{{\lambda }^{3}}} {{{H}^{2}}}}} \right. \kern-0em} {{{H}^{2}}}},$$

(2)

where ${{a}_{{\text{d}}}}$ is a dimensionless numerical coefficient depending on the shape of the initial elevation and the conditions for the visibility of dispersion effects (${{a}_{{\text{d}}}} \approx 0.06$ (Mirchina and Pelinovsky, 1982)); $\lambda$ is the wavelength.

The authors of (Glimsdal et al., 2013) proposed considering the “normalized dispersion time,” a dimensionless value defined by the formula

$$\tau = \left( {{{C}_{0}} - {{C}_{{{\text{ph}}}}}(\lambda )} \right){t \mathord{\left/ {\vphantom {t \lambda }} \right. \kern-0em} \lambda },$$

(3)

where ${{C}_{0}} = \sqrt {gH}$ is the long-wave speed; ${{C}_{{{\text{ph}}}}}(\lambda )$ is the phase velocity of gravity waves of length $\lambda ,$ which is calculated according to the classical formula: ${{C}_{{{\text{ph}}}}} = {\omega \mathord{\left/ {\vphantom {\omega k}} \right. \kern-0em} k} = {{\sqrt {gk\tanh (kH)} } \mathord{\left/ {\vphantom {{\sqrt {gk\tanh (kH)} } k}} \right. \kern-0em} k};$ $t$ is the wave propagation time; and $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ is the wave number. At $kH \ll 1$ (long waves), formula (3) can be represented in the following approximate form:

$$\tau \approx \frac{{6{{H}^{2}}L}}{{{{\lambda }^{3}}}},$$

(4)

where $L = {{C}_{0}}t$ is the distance traveled by a long wave in time $t$. According to what we will henceforth refer to as the “Glimsdal criterion,” dispersion effects are small at $\tau < 0.01$, and, when $\tau > 0.1$, these effects become significant.

The authors of the article (Glimsdal et al., 2013) note that their criterion is in line with the Kajiura criterion. Indeed, if we assume that the tsunami wavelength is equal to the horizontal extent of the source ($\lambda \approx a$), then the parameters $\tau$ and ${{p}_{a}}$ turn out linked by the formula

$$\tau = \frac{{36}}{{p_{a}^{3}}}.$$

(5)

In accordance with formula (5), the critical value of the parameter ${{p}_{a}} = 4,$ proposed by Kajiura corresponds to the value ${{\tau }_{{\text{K}}}} \approx 0.56.$ It can be seen that the Glimsdal criterion (even for ${{\tau }_{{\text{G}}}} = 0.1$) is more stringent than the Kajiura criterion.

It is easy to verify that the Pelinovsky criterion (2) also corresponds to the Glimsdal and Kajiura criterions. The dimensionless parameters included in formulas (1), (2), and (4) are interconnected by the following simple relationships:

$${{\tau }_{{\text{P}}}} = 6{{a}_{{\text{d}}}},$$

(6)

$${{a}_{{\text{d}}}} = {6 \mathord{\left/ {\vphantom {6 {p_{a}^{3}}}} \right. \kern-0em} {p_{a}^{3}}}.$$

(7)

Bearing in mind the numerical value of the parameter ${{a}_{{\text{d}}}} \approx 0.06,$ as indicated in (Mirchina and Pelinovsky, 1982), we can conclude that the value $\tau$ corresponding to the Pelinovsky criterion is ${{\tau }_{{\text{P}}}} \approx 0.36.$ Therefore, the Pelinovsky criterion in terms of severity occupies an intermediate position between the Glimsdal and Kajiura criteria: ${{\tau }_{{\text{G}}}} < {{\tau }_{{\text{P}}}} < {{\tau }_{{\text{K}}}}.$

All three criteria noted above were obtained by the authors from various theoretical considerations. Kajiura analyzed the asymptotic behavior of waveforms. Pelinovsky in (Pelinovsky, 1996) notes that his criterion follows from the linearized Korteweg–de Vries equation and from dimensional considerations. Formula Glimsdal (3) is based on the physics of the process: it describes the ratio of the difference in the distances traveled by the long and dispersive waves during the time $t$ to the wavelength. It is noteworthy that a similar physical approach to obtaining the desired criterion was proposed long before the publication of the article (Glimsdal et al., 2013) in (Kulikov et al., 1996).

The concepts of time and distance of dispersion destruction (“collapse time” and “collapse distance”) were introduced in (Kulikov et al., 1996):

$${{T}_{{\text{c}}}} = \frac{\lambda }{{\sqrt {gH} - {{C}_{{{\text{gr}}}}}}},$$

(8)

$${{D}_{{\text{c}}}} = {{T}_{{\text{c}}}}\sqrt {gH} ,$$

(9)

where ${{C}_{{{\text{gr}}}}}$ is the group velocity of gravity waves on water, determined by the dispersion relation in the traditional way (${{C}_{{{\text{gr}}}}} = {{d\omega } \mathord{\left/ {\vphantom {{d\omega } {dk}}} \right. \kern-0em} {dk}}$). The physical meaning of value ${{T}_{{\text{c}}}}$ is the time during which the wave packet lags behind the front by wavelength $\lambda$. Value ${{D}_{{\text{c}}}}$ is the distance at which the wave packet will lag behind the front by wavelength $\lambda$.

Note that E.A. Kulikov’s approach is distinguished by a clear physical interpretation of the introduced concepts, as well as the use of the group wave velocity ${{C}_{{{\text{gr}}}}}$ instead of phase ${{C}_{{{\text{ph}}}}},$ which is used by the authors of (Glimsdal et al., 2013). The approach proposed in (Kulikov et al., 1996) is more correct and universal: it can easily be extended to any type of wave (any type of dispersion relation). Note that, for long gravity waves on water ($kH \ll 1$), the difference between the phase and group velocities is small. However, for example, for long waves in a rotating ocean (Poincaré waves), which are characterized by the dispersion relation ${{\omega }^{2}} = gH{{k}^{2}} + {{f}^{2}},$ where $f$ is the Coriolis parameter (Grimshaw et al., 1998), the difference between the phase and group velocities can be of fundamental importance.

In our work (Nosov, 2017), it was shown that, when passing to dimensionless variables, formulas (8) and (9) merge into a single expression:

$$T_{{\text{c}}}^{*} = D_{{\text{c}}}^{*} = \frac{{\lambda {\text{*}}}}{{1 - C_{{{\text{gr}}}}^{*}}},$$

(10)

where $T_{{\text{c}}}^{*} = {{{{T}_{{\text{c}}}}} \mathord{\left/ {\vphantom {{{{T}_{{\text{c}}}}} {\sqrt {{H \mathord{\left/ {\vphantom {H g}} \right. \kern-0em} g}} }}} \right. \kern-0em} {\sqrt {{H \mathord{\left/ {\vphantom {H g}} \right. \kern-0em} g}} }},$ $D_{{\text{c}}}^{*} = {{{{D}_{{\text{c}}}}} \mathord{\left/ {\vphantom {{{{D}_{{\text{c}}}}} H}} \right. \kern-0em} H},$ $\lambda ^{*} = {\lambda \mathord{\left/ {\vphantom {\lambda H}} \right. \kern-0em} H},$ and $C_{{{\text{gr}}}}^{*} = {{{{C}_{{{\text{gr}}}}}} \mathord{\left/ {\vphantom {{{{C}_{{{\text{gr}}}}}} {\sqrt {gH} }}} \right. \kern-0em} {\sqrt {gH} }}.$ In the long-wave limit ($k^{*} = kH \ll 1$), from formula (10) we obtain

$$T_{{\text{c}}}^{*} = D_{{\text{c}}}^{*} \approx \frac{{4\pi }}{{{{k}^{{*3}}}}} = \frac{{{{\lambda }^{{*3}}}}}{{2{{\pi }^{2}}}}.$$

(11)

If in formula (11) we go back to dimensional quantities, then it is easy to make sure that it is equivalent to the Pelinovsky formula (2) for the value of the parameter ${{a}_{{\text{d}}}} = {1 \mathord{\left/ {\vphantom {1 {2{{\pi }^{2}}}}} \right. \kern-0em} {2{{\pi }^{2}}}} \approx 0.051,$ which is close to the critical value indicated in (Mirchina and Pelinovsky, 1982).

Concluding the review, we can find that all four approaches in the long-wavelength limit give formulas that include a single combination ${{{{\lambda }^{3}}} \mathord{\left/ {\vphantom {{{{\lambda }^{3}}} {{{H}^{2}}}}} \right. \kern-0em} {{{H}^{2}}}},$ but differ in “subjective” numerical factors proposed by various authors. The difference in the values of these factors makes it difficult to use the theoretical results in practice. In addition, for the practical application of the criterion, it is important to have a physically adequate method for determining the dominant wavelength. The fact is that grade time/distance dispersion destruction strongly depends on the wavelength ($T_{{\text{c}}}^{*} = D_{{\text{c}}}^{*}\sim {{\lambda }^{{*3}}}$). Therefore, even a small inaccuracy in determining the wavelength can significantly affect the result.

The main goal of this work is to develop a method for the quantitative determination of the time–space limits up to which the theory of long waves makes it possible to calculate dispersive tsunami waves with a given accuracy. Based on the theoretical concepts of time and distance of dispersion destruction introduced by Kulikov in (Kulikov et al., 1996), we adapt these concepts for practical application, indicating, in particular, the method for choosing the dominant wavelength.

2 WAVE PROPAGATION CALCULATION

We will consider the one-dimensional—along the horizontal axis $0x$—propagation of gravity surface waves in a basin of constant depth $H.$ All the following formulas, except where otherwise noted, will be presented in dimensionless variables. When dimensioning, we choose the depth as the length scale $H{\text{:}}$ $x^{*} = {x \mathord{\left/ {\vphantom {x H}} \right. \kern-0em} H},$ $k^{*} = kH$ ($k$ is the wave number). As a time scale, the propagation time of long waves over a distance equal to the depth $\sqrt {{H \mathord{\left/ {\vphantom {H g}} \right. \kern-0em} g}} ,$ where $g$ is the acceleration of gravity: $t^{*} = {t \mathord{\left/ {\vphantom {t {\sqrt {{H \mathord{\left/ {\vphantom {H g}} \right. \kern-0em} g}} }}} \right. \kern-0em} {\sqrt {{H \mathord{\left/ {\vphantom {H g}} \right. \kern-0em} g}} }}.$ The displacement amplitudes of the bottom surface and the free water surface are normalized to the maximum value of the residual displacement: $\eta^{*} = {\eta \mathord{\left/ {\vphantom {\eta {{{\eta }_{{\max }}}}}} \right. \kern-0em} {{{\eta }_{{\max }}}}},$ $\xi^{*} = {\xi \mathord{\left/ {\vphantom {\xi {{{\eta }_{{\max }}}}}} \right. \kern-0em} {{{\eta }_{{\max }}}}}.$ The sign * will be omitted in what follows.

As a source of waves, consider the residual displacement of the bottom surface $\eta (x)$ ($\left| \eta \right| \ll H$), which occurs instantly at a moment in time $t = 0.$ The instantaneous displacement of the bottom displaces water and forms a disturbance on the free surface ${{\xi }_{0}}$ (initial elevation), which is calculated using the following formulas (Nosov and Sementsov, 2014):

$${{\xi }_{0}}(x) = \int\limits_{ - \infty }^{ + \infty } {\frac{{B(k)}}{{\cosh (k)}}{{e}^{{ - ikx}}}dk} ,$$

(12)

$$B(k) = \frac{1}{{2\pi }}\int\limits_{ - \infty }^{ + \infty } {\eta (x){{e}^{{ikx}}}dx} .$$

(13)

An arbitrary one-dimensional traveling wave disturbance free surface can be represented as a Fourier integral:

$$\xi (x,t) = \int\limits_{ - \infty }^{ + \infty } {A(k){{e}^{{i\left( {\omega (k)t - kx} \right)}}}dk} ,$$

(14)

where $\omega (k)$ is the cyclic frequency depending on the wave number $k$. Dependency type $\omega (k)$ is determined by the dispersion relation, and the function $A(k)$ is determined by the form of the initial elevation. For the source described above, it looks like

$$A(k) = \frac{{B(k)}}{{\cosh (k)}}.$$

(15)

Note that the presence of an exponentially increasing function “$\cosh (k)$” in the denominator of formula (15) ensures that the spectral composition of surface waves is limited (the smoothing effect of the water layer). Due to the fact that it is the short-wavelength components of surface gravity waves that are most susceptible to phase dispersion, the correct consideration of the smoothing effect is important for the study. Therefore, as the source of waves, we set the initial elevation of the water surface, calculated from the residual displacement of the bottom, taking into account the smoothing effect.

Choosing different types of dispersion relations $\omega (k)$ in formula (14), one can calculate the wave profiles corresponding to different approximations. In this paper, we will consider two dispersion relations:

$${{\omega }^{2}} = k\tanh (k),$$

(16)

$${{\omega }^{2}} = {{k}^{2}}.$$

(17)

Formula (16) corresponds to the full dispersion theory of surface gravity waves on water, and formula (17) corresponds to the long-wave approximation.

The model residual displacement of the bottom, which we used in the calculations, is shown in Fig. 1. Like for almost all real tsunami sources, the bottom displacement consists of a region of uplift and a region of subsidence. The displacement is described by a piecewise linear function of the horizontal coordinate. The function parameters are the coordinates of four points (${{x}_{1}},$ ${{x}_{2}},$ ${{x}_{3}},$ ${{x}_{4}}$) or three corresponding lengths (${{a}_{1}} = {{x}_{2}} - {{x}_{1}},$ ${{a}_{2}} = {{x}_{3}} - {{x}_{2}},$ ${{a}_{3}} = {{x}_{4}} - {{x}_{1}}$), as well as the quantities ${{z}^{ + }}$ and ${{z}^{ - }},$ determining the amplitudes of bottom uplift and subsidence, respectively. In all cases it was assumed that ${{x}_{1}} = 0.$ The total length of bottom displacement area is $L = {{x}_{4}} = {{a}_{1}} + {{a}_{2}} + {{a}_{3}}.$

Fig. 1.

Geometry of the Model Wave Source. The residual displacement of the bottom is shown by a black solid line; the initial elevation of the water surface is shown by a gray dotted line.

The integral in formula (13) for the piecewise linear function shown in Fig. 1 is easy to calculate analytically

$$\begin{gathered} B(k) = \frac{{{{e}^{{ik{{x}_{1}}}}}{{z}^{ + }}}}{{({{x}_{1}} - {{x}_{2}}){{k}^{2}}}} + \frac{{{{e}^{{ik{{x}_{4}}}}}{{z}^{ - }}}}{{({{x}_{3}} - {{x}_{4}}){{k}^{2}}}} \\ + \,\,\frac{{{{e}^{{ik{{x}_{2}}}}}\left[ {{{z}^{ + }}({{x}_{1}} - {{x}_{3}}) + {{z}^{ - }}({{x}_{2}} - {{x}_{1}})} \right]}}{{({{x}_{2}} - {{x}_{1}})({{x}_{2}} - {{x}_{3}}){{k}^{2}}}} \\ + \,\,\frac{{{{e}^{{ik{{x}_{3}}}}}\left[ {{{z}^{ + }}({{x}_{4}} - {{x}_{3}}) + {{z}^{ - }}({{x}_{2}} - {{x}_{4}})} \right]}}{{({{x}_{3}} - {{x}_{2}})({{x}_{3}} - {{x}_{4}}){{k}^{2}}}}. \\ \end{gathered} $$

(18)

The integral in formula (14) was calculated numerically. Examples of wave profiles calculated using the full (16) and approximate (17) dispersion relations are shown in Fig. 2. We will discuss them in Section 5.

Fig. 2.

Examples of wave profiles calculated with and without dispersion (blue and red curves, respectively). In all cases, the calculation was performed for a moment of time equal to the dispersive destruction distance $t = \Delta .$ Source parameter values ($L,$ ${{a}_{1}},$ ${{a}_{2}},$ ${{a}_{3}},$ ${{z}^{ + }},$ ${{z}^{ - }}$), as well as the values of the coefficient $\alpha$ and parameter $\delta ,$ characterizing the degree of difference between dispersive and nondispersive wave disturbances, are shown in the figure. The insets show the amplitude spectra of the functions ${{d{{\xi }_{0}}} \mathord{\left/ {\vphantom {{d{{\xi }_{0}}} {dx}}} \right. \kern-0em} {dx}}$ and the values ${{k}_{{\max }}},$ which were used to calculate the dispersive destruction distance.

3 DISPERSIVE DESTRUCTION DISTANCE

In reality, tsunami wavelengths can be several hundred kilometers or more. The lagging of the wave packet behind the front by one wavelength, considered in the Kulikov criterion (Kulikov et al., 1996), in fact indicates a very significant dispersion transformation of the wave packet. Therefore, the time and distance of dispersion destruction determined by formulas (8)–(10) certainly cannot serve as a good practical criterion for the applicability of the theory of long waves. In addition, the practical use of formulas (8)–(10) requires the development of a methodology for determining the dominant wavelength.

In the development of Kulikov’s approach, we propose considering the delay of the wave packet from the front by a fraction of the wavelength: $\alpha \lambda ,$ where $\alpha$ is the correction factor. Then, based on formula (10), we can introduce a dimensionless characteristic, which we will call the “dispersion destruction distance”:

$$\Delta = \alpha \frac{{{{\lambda }_{{\max }}}}}{{1 - {{C}_{{{\text{gr}}}}}({{\lambda }_{{\max }}})}},$$

(19)

where ${{\lambda }_{{\max }}}$ is the wavelength that accounts for the maximum of the spatial spectrum of the function ${{d{{\xi }_{0}}} \mathord{\left/ {\vphantom {{d{{\xi }_{0}}} {dx}}} \right. \kern-0em} {dx}}.$ Thus, we calculate the dispersive destruction distance using the wavelength dominating in the tsunami spectrum. For convenience, instead of the wavelength in formula (19), we will operate with the corresponding wavenumber: ${{k}_{{\max }}} = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {{{\lambda }_{{\max }}}}}} \right. \kern-0em} {{{\lambda }_{{\max }}}}}.$

The use of the derivative ${{d{{\xi }_{0}}} \mathord{\left/ {\vphantom {{d{{\xi }_{0}}} {dx}}} \right. \kern-0em} {dx}}$ to find the maximum spectrum, and not function ${{\xi }_{0}}$ itself, has a simple physical justification. The fact is that the formation of gravity waves from the initial elevation is associated with the action of the horizontal component of the pressure gradient force, which is proportional precisely to ${{d{{\xi }_{0}}} \mathord{\left/ {\vphantom {{d{{\xi }_{0}}} {dx}}} \right. \kern-0em} {dx}}.$ When ${{d{{\xi }_{0}}} \mathord{\left/ {\vphantom {{d{{\xi }_{0}}} {dx}}} \right. \kern-0em} {dx}} = 0$, tsunami waves do not occur at all.

Applying formula (12), we find the first spatial derivative of the initial elevation

$$\frac{{d{{\xi }_{0}}}}{{dx}} = \int\limits_{ - \infty }^{ + \infty } {\frac{{B(k)k}}{{\cosh (k)}}{{e}^{{ - ikx}}}dk} .$$

(20)

Value ${{k}_{{\max }}}$ is determined by the position of the absolute maximum of the amplitude spectrum

$$S(k) = \frac{{\left| {B(k)} \right|k}}{{\cosh (k)}}.$$

(21)

Typical shapes of amplitude spectra (21) and examples of determining the value ${{k}_{{\max }}}$ are presented along with examples of wave profiles in Fig. 2.

4 QUANTITATIVE MEASURE OF DIFFERENCE IN WAVE PROFILES

As a quantitative measure of the difference between wave profiles obtained with and without allowance for dispersion, we will consider the following dimensionless parameter:

$$\delta = \frac{{\int\limits_{ - \infty }^{ + \infty } {{{{\left( {{{\xi }_{{\text{D}}}} - {{\xi }_{{{\text{LW}}}}}} \right)}}^{2}}dx} }}{{\int\limits_{ - \infty }^{ + \infty } {\xi _{{{\text{LW}}}}^{2}dx} }},$$

(22)

where ${{\xi }_{{\text{D}}}}$ is the wave profile calculated taking into account the dispersion (dispersion relation (16)) and ${{\xi }_{{{\text{LW}}}}}$ is the profile calculated according to the theory of long waves (dispersion relation (17)). The wave profiles were calculated at given times with a fixed spatial step. Therefore, in practical calculations, the integrals in formula (22) were replaced by sums in accordance with the method of rectangles.

Theoretically, the value of parameter $\delta$ varies within the following limits: $0 \leqslant \delta \leqslant 2.$ The minimum value of the parameter indicates the complete coincidence of the dispersive and nondispersive wave profiles, and the maximum value indicates the complete divergence of the wave profiles. Indeed, if, due to dispersion the profiles ${{\xi }_{{\text{D}}}}$ and ${{\xi }_{{{\text{LW}}}}}$ do not intersect in space at all, then ${{\xi }_{{\text{D}}}}{{\xi }_{{{\text{LW}}}}} = 0;$ hence,

$$\begin{gathered} \int\limits_{ - \infty }^{ + \infty } {{{{\left( {{{\xi }_{{\text{D}}}} - {{\xi }_{{{\text{LW}}}}}} \right)}}^{2}}dx} \\ = \int\limits_{ - \infty }^{ + \infty } {\xi _{{\text{D}}}^{2}dx} + \int\limits_{ - \infty }^{ + \infty } {\xi _{{{\text{LW}}}}^{2}dx} = 2\int\limits_{ - \infty }^{ + \infty } {\xi _{{{\text{LW}}}}^{2}dx} . \\ \end{gathered} $$

(23)

In formula (23), we took into account that the energies of traveling dispersive and nondispersive waves ($E = \rho g\int {{{\xi }^{2}}dx}$) caused by the same initial elevation coincide:

$$\int\limits_{ - \infty }^{ + \infty } {\xi _{{\text{D}}}^{2}dx} = \int\limits_{ - \infty }^{ + \infty } {\xi _{{{\text{LW}}}}^{2}dx} .$$

(24)

In addition to the parameter $\delta$, wave profiles were used to determine the amplitudes of the leading waves propagating in the positive and negative directions of the axis $0x.$ The amplitudes of the leading waves calculated taking into account dispersion were denoted as ${{A}_{{\text{D}}}}$ and, without taking into account dispersion, as ${{A}_{{{\text{LW}}}}}.$ Despite the fact that the area of bottom uplift was always located on the left and the area of subsidence was always on the right, the sign of the leading wave was not unambiguously related to the direction of propagation. Moreover, the signs of the leading waves calculated with and without allowance for dispersion often turned out to be different. In a number of cases, waves could begin with a very weak—visually indistinguishable—negative phase, followed by a positive wave of significant amplitude, and vice versa: a weak positive leading wave could be followed by a large-amplitude negative wave. In this regard, when identifying the leading waves, we considered only significant disturbances, which in amplitude exceeded 10% of the amplitude of the wave disturbance ($\max ({{\xi }_{{\text{D}}}}) - \min ({{\xi }_{{\text{D}}}})$ or $\max ({{\xi }_{{{\text{LW}}}}}) - \min ({{\xi }_{{{\text{LW}}}}})$). Level fluctuations of smaller amplitude were ignored when the leading wave was identified. The automatically selected amplitudes of the leading waves in Fig. 2 are marked on the wave profiles by bold dots.

5 MODELING TECHNIQUE AND RESULTS

The simulation was carried out by the Monte Carlo method. The parameters of the piecewise linear function describing the residual displacement of the bottom (Fig. 1) were set as follows. The total length of the source, as well as the amplitudes of the rise and fall of the bottom, varied statistically uniformly in the ranges $5 < L < 50,$ $0 < {{z}^{ + }} < 1,$ $- 1 < {{z}^{ - }} < 0.$ The coordinates of the points of maximum rise and fall of the bottom (${{x}_{2}}$ and ${{x}_{3}}$) randomly chosen inside the source region ($0 < x < L$) are also statistically uniform. At an ocean depth of 5 km, the chosen range of variation of the dimensionless value $L$ corresponds to the horizontal extent of the source from 25 to 250 km.

The calculation of the wave perturbation of the free surface caused by the instantaneous deformation of the bottom was carried out numerically in accordance with formula (14). Waveforms were calculated with a spatial step $\Delta x = 0.5.$ Taking into account the smoothing effect of the water layer, such a step was sufficient for an adequate discrete representation of the wave perturbation of the free surface.

Wave profiles were calculated at fixed times $t,$ which were equated to the dispersive destruction distance determined by formula (19): $t = \Delta .$ The quantities of the correction factor in formula (19) were set discretely: α = 1/32, 1/16, 1/8, 1/4, 1/2, 1, 2. For each fixed parameter value $\alpha$, 2000 wave profiles were calculated.

In numerical calculations of wave profiles, the dispersive destruction distance was limited by the maximum value ${{\Delta }_{{\max }}} = 2000,$ which, at an ocean depth of 5 km, corresponds to transoceanic wave propagation over a distance of 10 000 km.

Examples of wave profiles are shown in Fig. 2. Profiles calculated with allowance for dispersion (dispersion relation (16)) are shown in blue, and profiles calculated without dispersion (dispersion relation (17)) are shown in red. The black broken line corresponds to the residual displacement of the bottom; the brown dotted line corresponds to the initial elevation of the water surface. The green curves in the insets show the amplitude spectra of the functions ${{d{{\xi }_{0}}} \mathord{\left/ {\vphantom {{d{{\xi }_{0}}} {dx}}} \right. \kern-0em} {dx}}$ and the values ${{k}_{{\max }}}$ determined from these spectra. Above each wave profile, the values of the source parameters are given ($L,$ ${{a}_{1}},$ ${{a}_{2}},$ ${{a}_{3}},$ ${{z}^{ + }},$ ${{z}^{ - }}$), as well as the values of the coefficient $\alpha$ and parameter $\delta ,$ which characterizes the degree of difference between dispersive and nondispersive wave disturbances.

Figure 2 shows that the wave profiles calculated using different dispersion relations always differ from each other. In the case of a complete dispersion theory, a wave perturbation is a dispersive train of waves that transforms as it propagates. The long-wave theory gives a wave whose shape is equivalent to that of the initial elevation and remains the same as it propagates.

The example shown in Fig. 2a demonstrates a situation that often occurs at small values of the coefficient α ($\alpha = {1 \mathord{\left/ {\vphantom {1 {32}}} \right. \kern-0em} {32}}$) and small sources $L$ ($L = 7.27$). It can be seen that, in this case, the dispersive destruction distance turned out to be so small ($\Delta = 0.93$) that a wave for time $t = \Delta$ simply did not have time to go beyond the source. This means that the theory of long waves in this case is not capable of reproducing a tsunami wave outside the source.

Figure 2b shows the case of a source of significant horizontal extent ($L = 41.3$). Even with a small value of the coefficient $\alpha = {1 \mathord{\left/ {\vphantom {1 {32}}} \right. \kern-0em} {32}}$, the dispersive destruction distance turns out to be sufficient ($\Delta = 66.8$) in order for the theory of long waves to be able to reproduce the dispersive tsunami wave outside the source with good accuracy. It can be seen from the figure that the wave profiles calculated using different dispersion relations turn out to be very close ($\delta = 0.013$).

Figures 2c, 2d, and 2e show the profiles of the waves that were generated by the same source ($L = 17.6$), but calculated for different values of coefficient $\alpha$ (1/16, 1/8, 1/4). It is clearly seen how, with an increase in the value $\alpha$, the differences between the profiles increase and the quantitative measure of these differences increases—parameter $\delta$ (0.025, 0.070, 0.207). It should also be noted that for a wave propagating in the negative direction of the 0x axis (Fig. 2e), a feature arises in determining the sign of the leading wave: the positive leading phase of the dispersive wave becomes too weak, and a perturbation with a negative phase is determined as the leading wave. In this case, for a wave without dispersion, the leading wave remains positive.

The discrepancy in determining the signs of the leading waves begins to appear more often at large values of the coefficient $\alpha$. Another such situation is shown in Fig. 2e. Here it is implemented for a wave traveling in the positive direction of the 0x axis. A nondispersive wave starts from a negative phase, while a dispersive wave starts from a clearly defined positive phase.

For large values of the coefficient $\alpha$ ($\alpha \geqslant 0.5$), the differences between the wave profiles become fundamental (Figs. 2f, 2g, 2h). Dispersive waves always have an extended oscillating “tail,” in which a noticeable part of the wave energy is concentrated. Waves calculated without taking dispersion into account are compressed in space and almost always have a larger amplitude.

From the examples presented in Fig. 2, the following preliminary conclusion can be drawn. When using the theory of long waves, an acceptable accuracy of reproduction of dispersive waves is ensured when $\alpha \leqslant 0.25$ (Figs. 2a–2e). However, due to the significant variability of the source shape (even within the framework of the simple model we have chosen), in order to establish quantitative patterns, it is advisable to turn to an analysis of the distributions of the value δ and distributions of the amplitude ratio of the leading waves ${{{{A}_{{\text{D}}}}} \mathord{\left/ {\vphantom {{{{A}_{{\text{D}}}}} {{{A}_{{{\text{LW}}}}}}}} \right. \kern-0em} {{{A}_{{{\text{LW}}}}}}}.$

Figure 3 shows the distributions of value δ obtained at different values of coefficient $\alpha .$ It can be seen from the figure that the increase in $\alpha$ leads on average to an increase in the values δ and, at the same time, to a noticeable narrowing of distributions. This is the expected result: the propagation time of the wave is proportional to the parameter $\alpha ;$ therefore, an increase in this parameter should increase the differences between the profiles of dispersive and nondispersive waves, which, in turn, is accompanied by an increase in the value δ. The decrease in the distribution width is due to the fact that the value δ has a theoretical limit ($\delta < {{\delta }_{{\max }}} = 2,$ see Section 4). The existence of this limit begins to noticeably affect the result at $\alpha \geqslant 1{\text{/}}2$: the right edge of the distribution is noticeably twisted.

Fig. 3.

Magnitude distributions δ constructed for different values of coefficient $\alpha$ (indicated in the figure).

Figure 4 shows the distributions of the absolute value of the ratio of the amplitudes of the leading waves $\left| {{{{{A}_{{\text{D}}}}} \mathord{\left/ {\vphantom {{{{A}_{{\text{D}}}}} {{{A}_{{{\text{LW}}}}}}}} \right. \kern-0em} {{{A}_{{{\text{LW}}}}}}}} \right|.$ For coinciding signs of the leading waves (${{{{A}_{{\text{D}}}}} \mathord{\left/ {\vphantom {{{{A}_{{\text{D}}}}} {{{A}_{{{\text{LW}}}}}}}} \right. \kern-0em} {{{A}_{{{\text{LW}}}}}}} > 0$), distributions are shown in red and, for mismatched signs (${{{{A}_{{\text{D}}}}} \mathord{\left/ {\vphantom {{{{A}_{{\text{D}}}}} {{{A}_{{{\text{LW}}}}}}}} \right. \kern-0em} {{{A}_{{{\text{LW}}}}}}} < 0$), in blue. At $\alpha = 1{\text{/}}32,$ when the manifestations of dispersion are obviously insignificant, the amplitude ratio ${{{{A}_{{\text{D}}}}} \mathord{\left/ {\vphantom {{{{A}_{{\text{D}}}}} {{{A}_{{{\text{LW}}}}}}}} \right. \kern-0em} {{{A}_{{{\text{LW}}}}}}},$ as a rule, is close to 1, and the proportion of cases where the theories of long and dispersive waves give different signs of the leading waves is only 4.5%. It is noteworthy that the discrepancy between the signs of the leading waves in most cases is accompanied by significant differences in the absolute value of the amplitude. Growth in the size of $\alpha$ leads to a shift in distributions $\left| {{{{{A}_{{\text{D}}}}} \mathord{\left/ {\vphantom {{{{A}_{{\text{D}}}}} {{{A}_{{{\text{LW}}}}}}}} \right. \kern-0em} {{{A}_{{{\text{LW}}}}}}}} \right|$ to the left, to a broadening of the distributions, and to an increase in the proportion of erroneous determinations of the sign of the leading wave. At $\alpha = 2$, the peak of the distribution falls at 0.5, which indicates a twofold overestimation of the amplitude of the leading wave by the theory of long waves, while the proportion of erroneous determinations of the sign of the leading wave reaches 25.1%.

Fig. 4.

Distributions of the absolute value of the ratio of the amplitudes of the leading waves $\left| {{{{{A}_{{\text{D}}}}} \mathord{\left/ {\vphantom {{{{A}_{{\text{D}}}}} {{{A}_{{{\text{LW}}}}}}}} \right. \kern-0em} {{{A}_{{{\text{LW}}}}}}}} \right|,$ obtained for dispersive and nondispersive (long) waves. Distributions for leading waves of the same polarity are plotted in red (${{{{A}_{{\text{D}}}}} \mathord{\left/ {\vphantom {{{{A}_{{\text{D}}}}} {{{A}_{{{\text{LW}}}}}}}} \right. \kern-0em} {{{A}_{{{\text{LW}}}}}}} > 0$); blue indicates waves of different polarity (${{{{A}_{{\text{D}}}}} \mathord{\left/ {\vphantom {{{{A}_{{\text{D}}}}} {{{A}_{{{\text{LW}}}}}}}} \right. \kern-0em} {{{A}_{{{\text{LW}}}}}}} < 0$). Percentages indicate the proportion of relevant cases.

In Figs. 5 and 6, in which the dependences of the percentiles of the distributions are plotted depending on the value $\alpha$, it is possible to see in detail how the distributions change depending on coefficient $\alpha$. The upper horizontal axis of the graphs shows the values of coefficient $\alpha$ corresponding to the criteria that were previously obtained by other authors (Kajiura, 1963; Mirchina and Pelinovsky, 1982; Glimsdal et al., 2013; Kulikov et al., 1996). The correspondence of value $\alpha$ to the previously obtained criteria were set according to the long-wavelength limit, within which all criteria evaluate the distance at which the dispersion becomes significant, by a single formula of the following form: ${{C{{\lambda }^{3}}} \mathord{\left/ {\vphantom {{C{{\lambda }^{3}}} {{{H}^{2}}}}} \right. \kern-0em} {{{H}^{2}}}},$ where $C$ is a dimensionless constant.

Fig. 5.

Dependence of the percentiles of the distributions of value $\delta$ on the value of coefficient $\alpha .$ The black dotted line indicates the values of the coefficient $\alpha$ meeting the criteria previously established by other authors.

Fig. 6.

Dependence of the percentiles of the distributions of value ${{{{A}_{{\text{D}}}}} \mathord{\left/ {\vphantom {{{{A}_{{\text{D}}}}} {{{A}_{{{\text{LW}}}}}}}} \right. \kern-0em} {{{A}_{{{\text{LW}}}}}}}$ (at ${{{{A}_{{\text{D}}}}} \mathord{\left/ {\vphantom {{{{A}_{{\text{D}}}}} {{{A}_{{{\text{LW}}}}}}}} \right. \kern-0em} {{{A}_{{{\text{LW}}}}}}} > 0$) on the value of coefficient $\alpha .$ The black dotted line indicates the values of coefficient $\alpha$ meeting the criteria previously established by other authors.

Formula (19) proposed by us in this paper, after passing to the long-wavelength limit ($kH \ll 1$) and to dimensional variables, takes the form

$$\Delta \approx \frac{\alpha }{{2{{\pi }^{2}}}}\frac{{\lambda _{{\max }}^{3}}}{{{{H}^{2}}}}.$$

(25)

Kulikov’s definition of the dispersive destruction distance (Kulikov et al., 1996) corresponds to $\alpha = 1.$

According to the Kajiura criterion (Kajiura, 1963), if we put ${{\lambda }_{{\max }}} = a,$ we get

$$\alpha = \frac{{12{{\pi }^{2}}}}{{p_{a}^{3}}} \approx 1.85.$$

(26)

The Pelinovsky criterion (Mirchina and Pelinovsky, 1982), defined by formula (2) with ${{a}_{{\text{d}}}} = 0.06,$ corresponds to the following coefficient value:

$$\alpha = 2{{\pi }^{2}}{{a}_{{\text{d}}}} \approx 1.18.$$

(27)

The correspondence of value $\alpha$ to the Glimsdal criterion (Glimsdal et al., 2013), defined by formula (4), is given by the expression

$$\alpha = \frac{{{{\pi }^{2}}}}{3}\tau \approx \left\{ {\begin{array}{*{20}{c}} {0.329\,\,\,\,{\text{at}}\,\,\,\,\tau = 0.1,} \\ {0.0329\,\,\,\,{\text{at}}\,\,\,\,\tau = 0.01.} \end{array}} \right.$$

(28)

Figures 5 and 6 clearly show how the known criteria are ranked according to the degree of severity. The Kajiura criterion turned out to be the mildest of all. According to our estimates, this criterion actually turns out to be inoperable: an acceptable match of profiles (for example, $\delta < 0.3$) will be implemented in less than 1% of cases.

As the rigidity increases, the Kajiura criterion is followed by the Pelinovsky and Kulikov criteria, which are similar in numerical values. Neither criterion provide a fundamental improvement in the situation compared to the Kajiura criterion, and only the Glimsdal criterion for $\tau = 0.1$ is really able to match wave profiles with an accuracy of $\delta < 0.5$ in 75% of cases; in this case, the amplitude of the leading wave will be overestimated by no more than 2 times approximately in 90% of cases. The Glimsdal criterion at $\tau = 0.01$ ensures an accuracy of $\delta < 0.1$ for 90% of cases; in this case, the error in determining the amplitude of the leading wave will be less than 20% in about 90% of cases.

We emphasize that a decrease in value $\alpha$ in practice cannot be unlimited. Values of the coefficient that are too small, which guarantee a high degree of coincidence of wave profiles, in many cases will give such a small distance of dispersive damage that the wave will not have time to propagate beyond the source: such a calculation will not make practical sense in most cases.

6 CONCLUSIONS

When modeling a tsunami using dispersionless long-wave models, it should be taken into account that water waves are dispersive at any length, so their reproduction by a long-wave model always occurs with some error. The question is only what kind of error is permissible in solving a particular practical problem. In this regard, the simulation of tsunami waves, it is advisable to accompany the marking computational area, which will show the distance of dispersion destruction $\Delta$ corresponding to the expected accuracy of waves reproduction $\delta$ for a given providing probability.

For example, we are interested in an accuracy of $\delta < 0.4$ with a 90% chance. Then, according to the dependencies shown in Fig. 5, we determine the required value of the correction factor: $\alpha = 0.2.$ Next, the original two-dimensional problem on the Earth’s surface should be reduced to a set of one-dimensional problems, for example, along a set of great-circle arcs passing through the center of the tsunami source with a given step along the azimuth angle, or, which is perhaps more promising, along the wave rays emanating from the center calculated taking into account the distribution of depths. Value $\Delta$ is determined along each direction (or beam) separately, taking into account the actual depth profile. We will not dwell on the detailed development of the corresponding methodology and its verification here; this can be the subject of a separate study.

In conclusion, we note that, in addition to the classical dispersion of gravity surface waves on water considered in the paper, as well as the “secondary” dispersion effects mentioned in the Introduction, there is also a nonstandard dispersion due to the presence of small-scale irregularities in the bottom topography (Dobrokhotov et al., 2015, 2016). In the present study, such effects are not taken into account in any way. Their description, obviously, should include the spatial derivatives of the function describing the bottom topography, and the question of including the corresponding corrections in the dispersion relation is still open.